有偏置的Rabi模型的能谱与Berry相

于 婷 任学藻

(西南科技大学理学院 四川绵阳 621010)

在量子力学中，波函数的相位问题一直是很重要的概念。几何相位近几年受到国内外学者的大量关注。几何相位这一定义最初是由印度物理学家Pancharatnam[1]在1956年研究偏振光干涉的时候提出来的，但在当时并没有引起大家重视。1984年，英国物理学家Berry[2]发现，系统的哈密顿量在绝热循环演化过程中，量子态除了产生一个一定存在的动力学相位之外，还产生了一个只与系统空间演化路径有关的几何相位，这就是现在的Berry相，从此Berry相被广泛接受和深入研究。1987年Aharanov等[3]对Berry相做了推广，提出绝热并不是必要条件，波函数在非绝热循环演化过程中依旧会获得一个几何相位。1988年，Bhandari等[4]通过研究发现在非循环非幺正的量子体系中也存在Berry相。随着量子信息技术的高速发展，1999年，Zanari[5]提出Berry相可用于量子计算，接着Jozsa等[6]在2000年通过核磁共振技术证实了几何量子计算的可靠性。在物理学家们对Berry相的不断深入研究中，已经认识到了它的独特性和在量子理论中的重要性。Jaynes-Cummings模型在之前一直被认为是在量子光学系统里描述光与原子相互作用最简单解析求解的模型，但后来人们发现该模型的局限性，J-C模型作的旋波近似处理方法[7]在强耦合时会带来错误的计算结果。这是因为，在光与物质强相互作用下，反旋波项无法忽略，这时就需要用非旋波近似的Rabi模型[8]来展开计算与研究。2012年，Jonas[9]通过半经典近似的方法，发现非旋波近似Rabi模型没有Berry相，进而说明量子系统的Berry相是由旋波近似带来的一种误差。但这一结论很快被证实是不正确的。我们注意到Rabi模型的基态不是真空态，而是各种态的叠加，并且从理论推导中可以发现Rabi模型的Berry相与本征态下光子数的期望值成正比[10-12]，所以Jonas认为Rabi模型没有Berry相的结论是由于他采用了不适当的近似方法所导致的。我们将Rabi模型推广加上了偏置项，即模拟外加电场对量子比特的调控，并通过调整耦合强度的大小进行对比分析，观察Berry相位差的变化，探讨偏置项对Berry相的影响，这对于在量子模拟或量子计算中量子比特系统的调控具有重要意义[13]。

1 模型与推导

1.1 Rabi模型的Berry相

当单模光场与二能级原子作用时，Rabi模型的哈密顿量为:

(1)

其中:ω0为光场频率;a+(a)为光子的产生(湮灭)算符;ω为二能级间距;σz为自旋1/2的pauli矩阵;σ+和σ-是升降算符;g为耦合强度。

将式(1)用矩阵表示为:

(2)

为了方便计算，我们对哈氏量旋转90度，用下面的旋转变化来实现：

(3)

V+σzV=σx,V+σxV=-σz

(4)

因此旋转后的Rabi模型可以写成如下形式：

(5)

根据光子数态，具有一般广泛形式的奇偶宇称下的本征函数为:

(6)

其中:φ+(φ-)对应偶(奇) 宇称下的本征函数；M为截断数。很容易验证上述态是宇称算符的本征态。考虑宇称对称的波函数将极大简化求解过程[11-12]。

将式(6)代入薛定谔方程式(5)很容易得到系数之间的关系：

(7)

左乘〈m|，并考虑到Fock态的正交归一条件〈m|n〉=σmn，得到：

(8)

下面我们将方程式(8)写成矩阵形式：

(9)

(10)

其中：|g〉,|e〉分别表示原子的基态和激发态；|n〉为光场的Fock态。

对于不含时的哈密顿量的物理系统，Berry相的计算通常要引入一个相位转换算符U(φ)=e-iφa+a绝热地加在系统的哈密顿量上[14]，它能够导致场态的改变。当系统初态为本征态时，且参数φ从0～2π 绝热的变化时，Berry相可由下式给出：

(11)

(12)

1.2 有偏置项的Rabi模型的Berry项

我们将Rabi模型推广加上偏置项，可以在量子计算中得到更广泛的运用，该模型的哈密顿量为：

(13)

其中：ω0为光场频率；a+(a)为光子的产生(湮灭)算符；ω为二能级间距；σz为自旋1/2的pauli矩阵；σ+和σ-是升降算符；g为耦合强度；ε为偏置项的系数。

Rabi模型的哈密顿量的本征态的一般形式可表示为：

(14)

其中：|g〉,|e〉分别表示原子的基态和激发态；|n〉为光场的Fock态。

将式(14)展开：

(15)

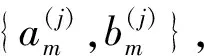
(16)

同样地，把一个相位转换算符U(φ)=e-iφa+a绝热地加在系统的哈密顿量上[14]，使参数φ从0～2π绝热地变化，当系统初态为能量本征态|Ψj〉时，Berry相为：

(17)

2 模拟与讨论

2.1 偏置系数对能谱的影响

取Rabi模型的4个能量较低的本征态，图1显示它在不同失谐量时能谱随耦合强度的变化，其中红色对应偶宇称，蓝色对应奇宇称；黑色对应偏置系数ε=0.1时的Rabi模型的能谱；紫色对应偏置系数ε=0.6时的Rabi模型的能谱。本文中ω0=1，失谐量Δ=ω-ω0。

从图1可以发现，在Rabi模型中，不论是共振还是失谐的情况下，它的能谱都几乎随耦合强度g的增加而单调下降，不同宇称相邻两能级的能谱曲线会随g的取值范围的变大而逐渐重合，而且奇偶宇称的相邻能级的激发态会发生能级交叉现象，同宇称的能谱一般不相交，只有不同宇称的能谱才会相交。只有在共振且g=0时，奇宇称相邻两能级的能谱才有交点。加小偏置(ε=0.1)时，它与Rabi模型的能谱基本重合，但是它的各级能谱曲线都不相交，特别是在Rabi模型能级交叉的简并点附近，它的能级结构发生了很大变化，在这里简并点的能级被打开，偏置项的存在破坏了Rabi模型的奇偶宇称。观察该简并点位置发现：图1(a)显示在共振Δ=0时，简并点在g=0.48左右；图1(b)显示在失谐量Δ=-0.5时，简并点在g=0.50左右；图1(c)显示在失谐量为Δ=0.5时，简并点在g=0.35左右。所以，该能量简并点的耦合强度会随失谐量的增加而减小。加大偏置(ε=0.6)时，各级能谱都不相交，呈单调递减趋势，并且随着正失谐量的增大，第二三能级的能谱在低耦合区(g≤0.30)会逐渐重合。

图1 Δ=0,-0.5,0.5情况下 Rabi模型(ε=0，0.1，0.6)的能谱的Ej/ω0关于g/ω0的函数Fig.1 Energy spectra Ej/ω0 of the Rabi model(ε=0，0.1，0.6) as a function of g/ω0 when Δ=0,-0.5,0.5

2.2 偏置系数对Berry相的影响

图2 Δ=0,-0.5,0.5情况下 Rabi模型(ε=0，0.1，0.6)的Berry相(γj)关于g/ω0的函数Fig.2 Berry phase (γj) of the Rabi model(ε=0，0.1，0.6) as a function of g/ω0 when Δ=0,-0.5,0.5

3 结论

在Rabi模型中，对于能谱，无偏置时奇偶宇称的相邻激发态能级会交叉，相同宇称的能级一般不会交叉，而有偏置时，所有能级都不会交叉。对于Berry相，在Rabi模型(ε=0)中，不同宇称的相邻两能级的Berry相会逐渐趋于一致，在加小偏置(ε=0.1)的Rabi模型中，j由小到大两相邻能级的Berry相会逐渐趋于一致，并且与Rabi模型的Berry相对比，除简并点附近基本一致，在能量简并附近的Berry相变化较大，这是由于Rabi模型系统的奇偶对称性被偏置项所破坏，宇称不再守恒所导致的。在加大偏置(ε=0.6)的Rabi模型中，当j≠0,2时，j由小到大相隔两个能级的Berry相会两两趋于一致，基态的Berry相与无偏置时基本相似，但高能级的Berry相与无偏置时有很大不同，说明偏置项的存在对高能级的Berry相影响较大。值得注意的是，当共振时，在弱耦合到强耦合变化的范围内，Rabi模型的所有激发态与基态的Berry相位差发生了π的奇数倍的改变，而加了偏置后所有激发态与基态的Berry相位差发生了π的偶数倍的改变，这在量子计算和量子模拟中具有重要意义。