基于ARIMA时间序列模型预测某三级甲等医院耐碳青霉烯类铜绿假单胞菌的感染率

高胜春 吴红梅

温州市人民医院感染管理科，325000浙江 温州

近年来，随着人口老年化及碳青霉烯类抗生素的过度使用，耐碳青霉烯类铜绿假单胞菌（carbapenemresistant pseudomonas aeruginosa，CRPA）菌株逐渐增多，已对临床控制医院获得性感染构成了严重威胁［1］。耐药性监测数据显示，我国2005—2014年对亚胺培南和美罗培南总的耐药率分别为31.8% 和28.6%，远高于欧美等国家［2-3］。监测的目的之一是预测，而现有的关于CRPA的研究大多集中于描述性研究。因CRPA数据存在较大的波动性，无法凭经验判断下一周期的数据，容易出现耐药菌传播或抗生素过度使用的情况。因此，运用数学模型对CRPA数据进行分析，预测其流行动态，对更好地掌握该耐药菌流行趋势具有重要意义。在传染病的短期预测中，常采用自回归移动平均模型（autoregressive integrated moving average model，ARIMA），它具有对复杂因素适应性强、模型结构简单、操作方便、经济实用等优点［4-5］。ARIMA既适用于平稳时间序列，也适用于非平稳时间序列。因此，它被广泛应用于季节性和周期性感染的预测。

本研究利用2016年1月至2019年12月浙江省某三级甲等医院CRPA感染率的监测数据建立ARI-MA时间序列模型，并利用模型对2020年1月至2020年9月的数据进行验证，为CRPA的管理和预警提供线索和科学依据。

1 资料与方法

1.1 资料来源与ARIMA乘积季节模型的建立

利用该院2016年1月至2019年12月的CRPA感染数据建立ARIMA时间序列模型，后利用模型对2020年1月至2020年9月的数据进行预测，以确定模型的平稳性和可用性。ARIMA时间序列模型基本结构为ARIMA（p，d，q）×（P，D，Q）s。其中，p为自回归阶项；q为移动平均项；d和D分别为提取原序列确定性信息和季节性的差分次数；P和Q则分别代表季节性自回归和季节性移动平均项；s为季节周期和循环长度。建立ARIMA模型包括4个主要步骤：

（1）序列平稳化。利用原始序列图和变换后的序列图来评价序列图的平稳性和趋势性。随后，通过差分或对数变换使有趋势性的非平稳序列ARIMA模型平稳可逆。

（2）模型识别和定阶。通过绘制平稳后自相关函数（ACF）和偏自相关函数（PACF），识别和分析时间序列的随机性、平稳性和季节性特征。根据BIC一般从0到2确定模型的阶数，阶数很少超过2，通过0、1和2的不同组合识别出几个粗略模型，最终选出BIC最小的最优模型。

（3）参数估计与诊断检验。用Box－Ljung检验识别残差序列的白噪声。即在残差相关检验中，残差必须是随机的（P＞0.05）。

（4）模型预测。采用最优ARIMA模型对2016年1月至2019年12月的CRPA感染数据进行回代模拟，再利用模型对2020年1月至2020年9月的数据进行预测，并通过计算平均相对误差来评价ARIMA模型的精度。

1.2 统计学方法

采用SPSS 25.0软件进行时间序列分析，定义时间变量。首先，将序列图与相关图和偏相关分析图相结合，判断其是否为平稳序列。如果不是平稳序列，则通过差分、季节差等方法将其转换为平稳序列，初步确定模型的取值范围。观察序列是否稳定的方法是观察序列图的均值是否发生显著变化。通过初步确定模型范围来进行模型预测，并使用Box-Ljung检验来确定其是否是白噪声序列，若Box-Ljung检验P＞0.05，则定为白噪声序列。如果多个模型通过Box-Ljung检验，则使用BIC来确定最优模型。

2 结果

2.1 CRPA感染情况及趋势分析

2016年1月至2019年12月共发生CRPA感染121例，感染率0.013% ～0.163%。依据CRPA感染率监测数据绘制时间序列图显示，CRPA感染全年每月均有发生，感染率波动较大并有一定的周期波动，不满足序列平稳性的要求。见图1。

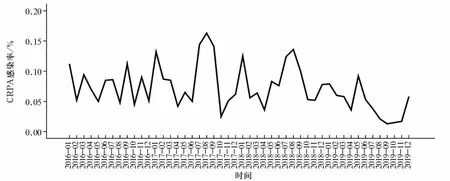
图1 CRPA感染率原始数据时序图

2.2 模型识别与定阶

由于原序列呈现出周期性季节波动的非平稳序列特点，因此需要建立混合效应模型（p，d，q）×（P，D，Q）s。一阶差分后的CRPA感染率的时序图见图2，ACF和PACF 图见图3。 模型形式为ARIMA（p，1，q）×（P，1，Q）12。利用SPSS的专家建模器从低阶到高阶逐个对p、q、P和Q的取值进行尝试，模型拟合的精度通过MAPE和BIC进行比较，取BIC值最小的为最佳模型。结果在建立的8个模型中有3个模型的参数通过统计学检验，比较各模型参数，最终确定最优模型为ARIMA（0，1，1）×（0，1，1）12。模型拟合正态化的BIC为3.461，决定系数R2为0.426，根据贝叶斯准则BIC值最小，R2最大为最优模型；Ljung-BoxQ检验显示差异无统计学意义（Q＝16.02，P＝0.38），属白噪声序列，提示本模型相对适合。

图2 CRPA感染率一阶差分后时序图

图3 CRPA感染率一阶差分后ACF图和PACF图

2.3 模型预测

2020年1月至2020年9月，CRPA感染率实际值与预测值大致相符。见图4。预测值与实际值的动态趋势基本一致，平均相对误差为8.45%。见表1。

表1 2020年1—9月CRPA感染率验证结果单位：%

图4 2016年1月至2020年9月CRPA感染率实际值与预测值的时间序列

3 讨论

目前耐碳青霉烯类铜绿假单胞菌具有多种耐药形式，呈现出从单一耐药到多药耐药，从低耐药到高耐药的趋势，这给临床治疗铜绿假单胞菌感染带来了巨大的压力。时间序列预测方法是对时间序列进行汇编和分析，根据时间序列对发展过程、方向和趋势的反映，通过类比或延伸的方法来预测未来一段时间或几年内可能达到的水平。其中，ARIMA模型能够综合序列的平稳性、季节性和随机性，不断修正模型，直到选定最优模型进行疾病研究，已成为应用最广泛的时间序列预测模型之一。本研究基于ARIMA乘积季节模型预测耐碳青霉烯类铜绿假单胞菌流行趋势为多重耐药菌控制策略的制定提供依据，旨在减少CRPA感染的发生。

本研究对浙江省某三级甲等综合医院CRPA感染资料进行了分析。通过ARIMA模型，根据BIC标准选择最优模型。结果表明，ARIMA（0，1，1）×（0，1，1）12模型是CRPA感染率发生的最佳模型。预测值与实测值吻合较好，平均相对误差为8.45%。各种时间序列模型或方法已被用于预测每月多重耐药菌的感染率。在移动平均、人工神经网络、线性回归和Holt－Winters模型等其他预测方法中［6-8］，ARIMA模型也被证明是比较适合预测多重耐药菌感染率的模型。一般来说，多重耐药菌感染并不像疟疾、白喉、水痘、轮状病毒、霍乱等疾病那样表现出明显的季节性［9-10］，然而一些研究已经使用季节性ARIMA模型研究了多重耐药菌的季节性影响。储文杰等［11］基于ARIMA乘积季节模型预测产超广谱β-内酰胺酶大肠埃希菌流行趋势，结果表明产超广谱β-内酰胺酶大肠埃希菌检出高峰出现在夏秋季节。刘燕等［12］利用ARIMA模型对2016年1—12月多重耐药鲍曼不动杆菌医院感染检出率流行趋势进行了预测，平均相对误差为8.45% 。

尽管本研究构建的ARIMA乘积季节模型预测结果较为理想，但与CRPA实际感染率相比仍存在偏差。原因在于本研究建模过程中仅考虑了时间因素，人口统计学和共病变量，如年龄、性别、社会经济地位和糖尿病，以及与多重耐药菌传播相关因素都没有被考虑在这项回顾性研究中。因此，必须谨慎地解释预测结果。此外，这项研究是基于浙江省某1家三级甲等医院数据进行的，因此，结果可能不适用于其他类型医院。然而，细菌耐药性是一个复杂的、持续进化的问题，经常是难以预料的。尽管研究者们在努力找寻解决细菌耐药性的方法，但一些非常简单的办法如减少抗生素的使用和开发高效的新药物在实际应用时却又非常艰难，因此，这项研究的结果有助于预测CRPA感染率的变化趋势，帮助医护人员及时采取感染防控措施，合理分配和使用卫生资源。