分数布朗运动随机微分方程解的逼近问题
2021-12-14宋艳英
宋艳英
(忻州师范学院 五寨分院,山西 五寨 030000)
长期以来,布朗运动一直是自然科学、金融市场等领域研究过程中应用较为广泛的随机性模型之一.布朗运动具有独立的增量,因此由该运动所产生的随机噪声可以定义为“白色”,即不相关.然而,自然科学、计算机网络、金融市场等领域在研究过程中具有长期依赖性,即研究过程中所产生的随机噪声的相关性可随时间的推移而缓慢降低,因此,在对上述过程进行建模的过程中通常会使用分数布朗运动.
在对分数阶布朗运动的随机微分方程进行研究的过程中[1-2],通常可以借助以下事实进行解释:分数布朗运动的积分情况定义方法有很多,其中应用最广泛的莫过于按路径定义,文献[3]将其定义为杨氏积分.在文献[4]中,对于任意H使用了所谓的“粗糙路径”进而构造了一个随机积分.分数阶Brownian的路径式随机微分方程运动,在长期依赖H> 1/2的情况下证明了解的存在性和唯一性[5],并且对于H> 1/4也进行了补充.另一种方法则是使用内核生成的空间,文献[6]主要考虑了具有此类积分的随机微分方程.文献[7]提出了随机积分的一般路径构造的情况.文献[8]主要研究了随机微分方程.文献[9]中考虑了具有Skorokhod积分的方程.在许多情况下,分数布朗运动方程的分析相当复杂.因此,对这些方程式进行近似解处理显得非常有必要. 分数布朗运动的近似问题包含基础建模,许多学者都考虑过这一问题.最简单的方法就是随机微分方程中的时间离散化方法.文献[10]对布朗运行的随机积分近似问题进行了研究,仅涉及分数布朗运动本身的收敛以及相关分数布朗运动足够光滑过程中的随机积分.因此,它们不能用于随机微分方程解收敛性的证明.
针对文献[10]中存在的问题,本文通过绝对连续的过程近似地研究分数布朗运动,证明了一个观点即与文献[10]相比近似的收敛性更强,也证实了相应随机微分方程解的收敛性.
1 问题陈述
1.1 分数微积分的元素
在本小节中充分考虑路径积分的基本构造.设f∈L1(a,b)以及α>0.α阶函数f左右的Riemann-Liouville积分几乎均被定义在x∈(a,b)范围内,有
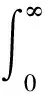

在极限f(a+)和g(b-)均存在且为有限的情况下,有
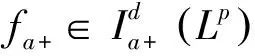
f(a+)(g(b-)-g(a+)) .
(1)
该定义使人们在满足Hölder条件的功能前提下,明确Cλ[a,b]也是满足Hölder条件并且指数为λ的函数空间,即
|f(x)-f(y)|≤C|x-y|λ,x,y∈[a,b].
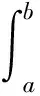
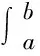

maxi|xi+1-xi|.
1.2 分数布朗运动
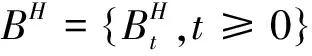
也被称为Hurst参数,或者H∈(0,1)的分数布朗运动.
不难看出,分数布朗运动的增量满足等式
因此,由于BH是一个高斯过程,它在Kol mogorov定理的基础上实现了较为连续的变型. 此外,其计算路径就在Cβ[0,T],T> 0且β∈(0,H)的条件下运行的.
(2)
其中{Wt,t≥0}是维纳过程,在α=H-1/2的条件下,常数CH为
1.3 分数索伯列夫空间
对于b∈(0,1)表示为


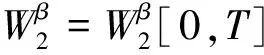
对于任何0 <ε<β∧(1-β),有
因此,对于几乎所有分数布朗运动BH的路径都在ω∈Ω和T> 0且0 <β 对于分数布朗运动的近似构造,借助文献[10]中提出的思想.请注意无法更改式(2)中的积分顺序并编写,有 因为内部积分是发散的,因此该想法是想要其在内部积分中与u发生“偏离”. 因此,构造了绝对连续过程的分数布朗运动的近似值,即 (3) (4) 这里的实数是可测量的,非递减函数的集合φε:[0,T]→[0,T],ε∈(0,1),满足以下条件: 1)φε(0)=0,0<φε(t) 2) |φε(t)-φε(s)|≤L|t-s|,t,s∈(0,T]; 在文献[10]中证明了对于任意β∈(0,1-H),都具有 (5) 定理1 对于任意γ∈(0,H),均可以发生以下收敛现象,即 证明根据定义,有 而且 并且φ-1表示为φ相反的函数. 下面来证明对于0<δ<2(H-γ),以下估计结论是正确的,则 t,s∈[0,T], (6) 假设0≤s 情况1t>s>φε(t)>φε(s),凭借等距的性质可以得出以下结论,即 分别对这3个积分进行估计.对于分数布朗运动,有如下的应对策略,即 因此, 3|t-s|2H≤3|t-s|2H-δ(t-φε(t))δ≤ 因此,在情况1中实现了对估计式(6)的证明. 情况2t>φε(t)>s>φe(s).,在这种情况下进行了如下处理,即 J1+J2+J3. 估计的这3个积分情况分别为 C1(H)(s-φε(s))2H≤ C1(H)(φe(t)-φε(s))2H-δ(s-φε(s))8≤ C2(H)|t-s|2H-δ(s-φe(s))δ, C1(H)|t-s|2H-8(t-φε(t))δ. 因此,情况2也证明了估计式(6). (7) 式中:CH,p为常数. 接下来,需要一个在t和s中均等的估计值,对于任何p> 0和α> 1/p,以下不等式均为真的,即 (8) 对于p>1/H,δ∈(0,H-1/p)和α∈(1/p, H-δ),有 考虑到式(8),将θ∈(γ,H)分别设置为p=2/(H-θ),α=(θ+H)/2和δ=(H-θ)/4. 从最后的估计结果得出,对于任何θ∈(γ,H)和κ∈(0,1),都存在一个常数Cκ,那么该事件的可能性 不小于1-κ. 在集合A_{e}上,对于所有s,t∈[0,T],可以得到 当 然后对于任何a> 0,都有 因为 对于足够小的ε,当κ→0+时,将得到 t∈[0,T], 给出了该方程解的存在性和唯一性的条件.因此以下证明或结论是正确的. 表示 X(ω,·)∈C1-α[0,T]. 参考BH过程,其中{BH,ε,ε>0}. 设Xε为等式 t∈[0,T]. 定理2 满足条件(Hb)和(Hσ),并且对于特定的γ∈(1/2,H),有 然后 为了证明该定理,需要进行以下引理操作. 1) 存在以下积分: t∈[0,T]; 3) ∣G(σ,g)(f)‖0,β,λ≤C1Λ1-β(g)λ2β-1(1+ ‖f‖0,β,λ),其中C1仅取决于β,T和σ; R的范围内存在一个 ‖G(σ,g)(f)-G(σ,g)(h)‖0,0≤ C2λ2β-1Λ1-β(g)(1+Kf+Kh)‖f-h‖0,β,λ, 并且 式中:C2仅取决于β、T、R和σ. Λ1-β(g)≤C‖g‖1,1-β. 引理2 设β∈(0,1/2),同时满足条件 并且对于任何λ≥1,以下断言均成立: 1) 存在勒贝格积分 2)F(b)(f)∈C1-β[0,T] ; 3) ‖F(b)(f)‖0,β,λ≤C3λ2β-1(1+‖f‖0,β,λ), whereC3depends only onβ,T, andb; ‖F(b)(f)-F(b)(h)‖0,β,λ≤C4λβ-1‖f-h‖0,β,λ, 式中:C4仅取决于β、T、R和b. 证明首先,需要证明KX2在ε中均匀地以概率为界. 很明显能够得到以下结论,即 根据文献[3]中的定理5.1,有 ‖Xε‖0,β≤2(1+|X0|)eλ0(ε)T, 并且 λ0(ε)≤(2(C3+C1Λ1-β(BH,ε)))1/(2β-1). 因为 Λ1-β(BH,ε)≤‖BH,ε‖1,1-β, 并且 R)→0,ε→0+. 使用引理1~2,可以得到 ‖X-Xε‖0,β,λ≤Cλ2β-1(1+‖BH|1,1-β)(1+ KX+KXe)‖X-Xε|0,β,λ+Cλ2β-1‖BH-BH,ε‖1,1-β(1+ ‖Xε‖0,β,λ). 如果 Θ(λ,ε)=Cλ2β-1{(1+‖BH‖1,1-β)· 则 因此 P(‖X-Xε‖0,β,λ>c)≤P(‖BH- BH,ε‖1,1-β>c)+P(Θ(λ,ε)>1/2), 因此,对于任意的δ> 0,有 BH,ε‖1,1-β>δe-λT)+P(Θ(λ,ε)>1/2). 为此较容易证明Θ(λ,ε)→0在ε中的概率均匀地分布在λ→∞范围内. 本文通过绝对连续的过程近似地研究分数布朗运动,证明了关于随机微分方程解的收敛性的一个一般性定理.作为推论,得到了关于具有绝对连续过程的随机微分方程解的收敛性与具有布朗运动方程的解的收敛性的结果.2 绝对连续过程逼近分数布朗运动
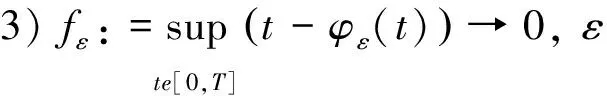

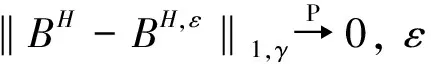

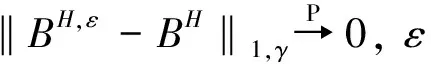

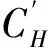
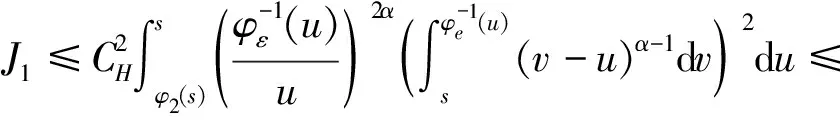

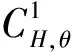
3 随机微分方程解的逼近
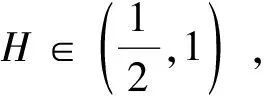
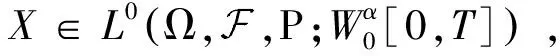
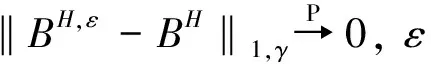
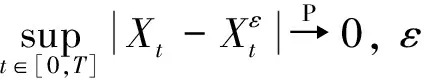
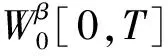


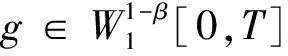

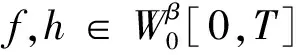
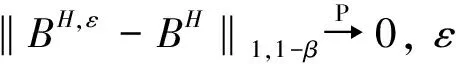
4 结论
