一种求解Lasso问题的不精确邻近梯度算法

2021-12-14谢秋玲徐宇淼胡清洁

桂林电子科技大学学报 2021年3期

谢秋玲, 徐宇淼, 胡清洁

(桂林电子科技大学数学与计算科学学院,广西桂林 541004)

最小绝对值收缩和选择算子(least absolute shrinkage and selection operator,简称Lasso)问题由Tibshirani[1]提出,即利用l1正则化项求解线性回归问题的稀疏解。Lasso问题在稀疏规划和信号处理领域起着非常重要的作用,其应用包括稀疏信号修复、稀疏图回归、稀疏逆协方差、稀疏字典学习、图像修复、图像去噪和去模糊等[2]。因此,在理论和算法上深化和完善对该问题的研究,具有重要的理论意义和广泛的应用前景。

Lasso问题模型如下:

在利用邻近梯度法求解问题(1)时,需计算邻近算子[7]:在很多情况下,邻近子问题(2)无解析解或者精确求解的计算量较大,需考虑近似求解邻近算子。鉴于此,提出了一种带有邻近算子误差和梯度计算误差的不精确邻近梯度算法,并给出该算法的收敛速度分析和相应的数值实验。

1 不精确邻近梯度算法

与文献[5]中提出的FISTA-BKTR 算法相比,为了加速收敛,本算法在步骤5)中计算不精确邻近算子,即考虑在问题(1)中光滑项梯度计算和求解邻近子问题时存在误差。

根据算法中的步骤2),若选择的μ-k、μ0k分别满足μ0>1/L(f)、μk≥μk-1,则对∀k,有μk≥β/L(f)。若μ0>1/L(f),因此有

2 算法的有关性质

性质1[7]若

引理3 若对任意的y∈Rn,μ>0,使得

类似于文献[7],可得如下关于不精确邻近梯度算法的2个关键引理。

引理5 若假设算法中满足

3 收敛速度分析

为了得到形如

定理1 若上述假设成立,则在算法的第k次迭代中,

其中,

即

由引理6可得

其中:

从而定理得证。

4 数值实验

分别用FISTA[4](加速邻近梯度算法)、INEXACT FISTA (不精确加速邻近梯度算法)、RS-FISTA[8](重启的加速邻近梯度法)、FISTA-BKTR(线搜索加速邻近梯度算法)、INEXACT FISTA-BKTR[5](不精确线搜索加速邻近梯度算法)求解Lasso问题,全部数值实验使用MATLAB语言编程,并在MATLAB R2016a中运行,测试环境为Window 7操作系统,Inter(R)Core(TM)i5-6500 CPU@3.20 GHz、8.00 GiB RAM。

在INEXACT FISTA 及INEXACT FISTABKTR算法中利用RCD[10](随机坐标下降算法)求解不精确邻近算子,即满足式(3)。然而,在这2种算法中,使用了文献[10]提出的内部停止条件,该停止条件保证了不精确算法可以达到快速局部收敛。梯度误差为e k=(0.001)k e,其中e=(1,0,…,0)T。经测试,将最高的迭代次数设置为500次。在问题(1)中,数据生成方法如下:

2)b∶=Ax++N(0,10-3),其中x+为利用标准高斯分布生成的s-稀疏向量。

令p=200,n=350,s=100,ρ=0.1。算法运行结果如图1、2和表1所示。

表1 算法比较结果

图1 5种算法目标函数值相对误差变化图

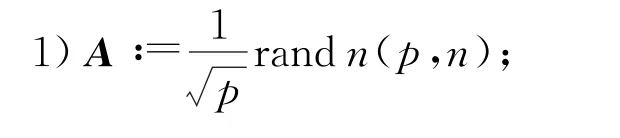
由上述实验结果可知,FISTA 和INEXACT FISTA算法在停止迭代时,INEXACT FISTA 得到的误差更小。FISTA-BKTR 和INEXACT FISTABKTR算法在满足停止条件时,INEXACT FISTABKTR所需的迭代次数更少。因此,与FISTA、FIS TA-BKTR相比,带有不精确邻近算子的INEXACT FISTA 和INEXACT FISTA-BKTR 的结果较好。通过对比可知,求解Lasso问题时,在相同条件下达到停止条件,INEXACT FISTA-BKTR 所需的迭代次数最少。