一类四次分片光滑广义Riccati系统的极限环与局部临界周期分支

曹成成, 黄文韬

(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;2.广西师范大学 数学与统计学院,广西 桂林 541004)

随着科技的发展,物理、化学等领域的许多模型需要分片光滑系统来描述。因此,对这类系统的研究具有重要的理论意义和应用价值。分片光滑系统经常在自动控制、力学及工程的不同领域中遇到[1-11]。文献[12]考虑了一个二次Bautin分片光滑系统,得到在系统原点的充分小邻域内有10个小振幅极限环的结果。文献[13]改进计算Lyapunov常数及周期常数的方法,并证明在三次分片光滑系统中至少有15个极限环。文献[14]研究了一个四次分片光滑系统,得到在系统双同宿环附近有11个极限环。文献[15]首次研究三次分片光滑系统临界周期分支问题,该系统在单一中心可分出5个临界周期分支。

文献[16]给出了广义Riccati系统的定义:

将上述系统扩展,考虑如下四次广义Riccati分片光滑系统:

研究系统原点的极限环与临界周期分支问题,并证明了该系统在原点邻域内有9个极限环和4个临界周期分支。

1 预备知识

考虑如下分片光滑系统:

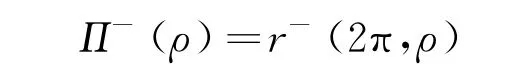
分别为正向后继函数和负向后继函数。系统(2)的后继函数如图1所示。

图1 系统(2)的后继函数

其中,V k为分片光滑系统(1)在原点处第k个Lyapunov常数。

若V1=V2=…=V k=0,V k+1≠0,则称系统(2)的原点为k/2阶细焦点;若k=0,则称原点为粗焦点;对于任意的k,都有V k=0,则原点就称作中心。

文献[13]给出了一种计算Lyapunov常数的方法,文献[13]、[17]、[18]给出了判定系统原点是中心的几个判据。

引理1[13]系统(2)原点成为中心的充要条件为下列2组条件之一成立:

1)系统(2)关于x轴对称,即

因此可得

若P1=P2=…=P k=0,P k+1≠0,则称系统(2)的原点为(k-1)/2阶细中心;若k=0,则原点就称为粗中心;若对于任意的k,都有P k=0,则原点就称作等时中心。

定义1[15]记Λ为系统(2)系数参数向量。对于参数λ*∈Λ时,系统(2)的原点为细中心,若存在ε0>0,使得任意的0<ε<ε0和每个λ*的充分小邻域W,并存在一个λ1∈W,使得P'(ρ,λ1)在U=(0,ε)内有k个解,则称在λ*下系统有k个临界周期从原点分支出来或称系统原点有k个临界周期分支。

引理2[19]

若存在参数

则对于λ=λ*做适当小的扰动,可以使得系统(2)从原点处恰有k个局部临界周期分支。

2 系统的Lyapunov常数及中心条件

应用文献[13]的计算方法,利用计算机代数软件Mathematica,通过仔细的计算和化简,有

定理1 系统(1)在原点处的前10个Lyapunov常数为

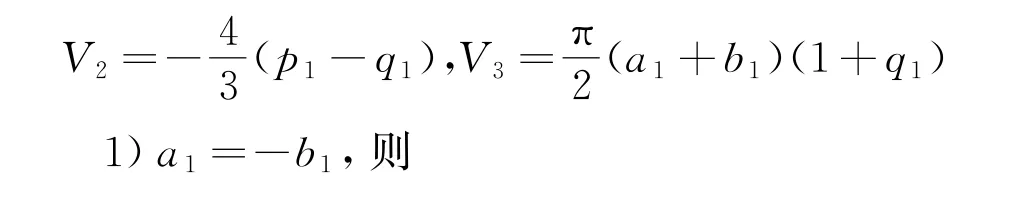
以下讨论系统(1)的中心问题,结合定理1,有如下定理。

定理2 系统(1)在原点的前10个Lyapunov常数为零,当且仅当以下条件成立:

证明 定理2的充分性易证,仅证明定理的必要性。

由V2=V3=0,可得到定理1中的2种情形。若情形1成立,则容易得到式(10)。若情形2成立,即q1=-1,则由V4=0,有a2=b2。由V5=V6=0,分别可得:

计算F1、F2、F3、F4关于变量a1、b1、b2的Gronber基:

由此得F1=F2=F3=F4=0无公共根,所以在情形2下前10个Lyapunov常数不全为零,即条件(10)成立。

定理3 系统(1)中的原点成为中心,当且仅当定理2中的条件(10)成立。

证明 若定理中2的条件成立,则系统(1)可写为

显然,系统(11)的上系统和下系统是关于x轴对称的,即在该条件下系统(1)的原点为中心。

3 系统原点的极限环

定理4 系统(1)的原点成为9/2阶细焦点的充要条件为

从定理2的证明中取满足条件(12)的一组实数解:

由定理2的证明可知,原点为细焦点的最高阶数是9/2。

由文献[20]的引理4可得如下引理:

引理3 若存在参数

对于λ=λ*做适当小的扰动,可以使得系统(1)在原点处有k个极限环。

定理5 当系统(1)的原点成为9/2阶细焦点时,通过对系统的系数进行适当的扰动,系统在原点充分小的邻域内可分支出9个小振幅极限环。

证明 由定理4可知,当条件(12)成立时,原点是系统(1)的9/2阶细焦点。通过计算雅可比行列式可得

由引理3知系统(1)在原点的充分小邻域可分支出9个极限环。

4 局部临界周期分支

当系统(1)原点的中心条件(10)成立时,得到下列周期常数:P1=-16b/3,当P1=0时,可得

通过GroebnerBasis[{f1,f2},{q1}]={1}或者解方程方法,可知f1=f2=0无公共根,即前4个周期常数均为零时,第5个周期常数P5≠0。因此,容易得到如下定理:

定理6 在条件(10)下,系统原点是3/2细中心的充要条件为

求解方程f1=0,q1有4组实数解,取其中一个实数解(精确到小数50位)为

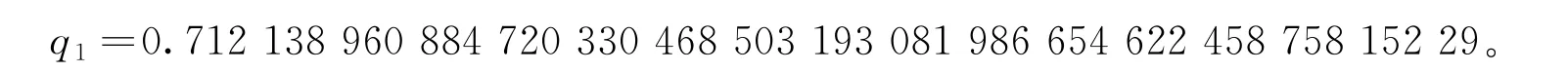
由于以下Jacobian行列式为

由文献[19]定理2可得:

定理7 若条件(10)成立,通过一定的扰动,系统(1)在原点邻域可分支出4个临界周期。

5 结束语

研究了一类分片光滑广义Riccati系统的极限环与临界周期问题,通过计算Lyapunov常数得到了中心条件,证明了该系统在原点邻域内有9个极限环,并在中心条件下,证得该系统在原点邻域内有4个临界周期分支。