领导-跟随多智能体系统在自适应牵制控制下的部分分量一致性

刘雪雪, 李丰兵, 马忠军

(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)

随着计算机通信及传感器网络技术的日益发展,多智能体系统协调控制的应用越来越广泛,从而引起了各领域学者的极大关注。许多学者将其关键技术应用到编队控制、集群问题、无人机协调控制等领域并取得了巨大进展[1-4]。多智能体系统协调控制主要研究群集[5]、跟踪[6]、聚集[7]、一致性问题[8-11]等,其中有关一致性的研究是目前比较关键和热门的。

一致性问题是指通过相互耦合作用或设计适当的控制器,使系统的状态变量随时间最终收敛到最佳状态。典型的控制方案包括牵制控制、脉冲控制、间歇控制、自适应控制、反馈控制等。当系统受到不稳定扰动时,自适应控制器能随之变换参数并产生协调作用,使系统最终仍能步入正轨并达到最优状态。该控制方案已被应用到计算机控制、稳定性理论、非线性系统等领域。近年来,多智能体系统的一致性问题中也大量涉及了适应性算法[8-10]。例如,文献[8]运用自适应控制算法探讨了具有非线性动态的高阶多智能体系统基于观测器的一致性,给出了系统实现一致的充分性判据;文献[9]讨论了自适应间歇控制下含有混合时延和未知参数的领导-跟随非线性多智能体系统的一致性问题;文献[10]不仅在文献[11]的基础上考虑了系统个体自身动力学的滞后效应,还运用分布式自适应控制方法,推出了该系统的滞后一致性准则。此外,复杂网络同步与多智能体系统的一致性问题紧密相关[12]。

以往关于智能体的所有状态变量趋于一致的研究相对较多,而关于部分分量的动力学行为的探究常被忽略。实际上,在现实生活中广泛存在只依赖于局部变量稳定性的部分分量一致行为。如在无人机飞行实验时,多架无人机在空中摆出各种各样的阵型,在其飞行前进方向上的位移分量可达一致,而在其他方向上的分量未能实现一致,即实现部分分量一致。受此类现象启发,很多学者对此进行了各类研究。例如,文献[13]给出了多智能体系统的部分分量一致性的概念,并基于矩阵论和稳定性理论,得到了实现该一致性的充分条件;文献[14]提出脉冲微分系统部分变元稳定性理论并进行了证明,探究了基于脉冲控制下一阶非线性多智能体系统的部分分量一致性问题;文献[15]采用间歇控制和牵制控制相结合策略导出了领导-跟随多智能体系统的部分分量一致性准则。由于现实生活环境的不定性及复杂性,网络中的全局信息是不断变化的。自适应控制增益可以适当减弱信息变化对一致性的影响。鉴于此,设计了一种适应性牵制协议,利用矩阵理论、图论及部分变元稳定性等理论,借助Lyapunov函数推出合理可行的结论,从而探究多智能体系统部分分量一致性问题。

1 预备知识

1.1 稳定性理论

考虑n维非自治微分方程组[16]

1.2 矩阵论

引理1[17]设

则存在n N阶置换矩阵P=P k P k-1…P1,其中P i为第一类初等行变换矩阵,i=1,2,…,k,k为正整数,使得

成立,其中⊗为克罗内克积。

引理2[18]对于矩阵A、B、C、D,其克罗内克积符合以下运算律:

1)(A+B)⊗C=A⊗C+B⊗C;

2)(A⊗B)(C⊗D)=(AC⊗BD);

3)(A⊗B)T=AT⊗BT;

4)(k A)⊗B=A⊗(k B)。

1.3 图论

设N阶有向图

为点集,E⊆V×V为边集,A为图G的加权邻接矩阵,a ij≥0表示节点v i和v j之间的权重连接, (v i,v j)为图G的边,当节点v j可以接收到节点v i传递的信息时,

则

图论作为一致性研究的重要工具,拓扑图可以反映各智能体之间的信息交流,其中节点表示各个智能体,边表示智能体之间的信息交互。

2 主要结果

假设由一个领导智能体和N个跟随智能体构成的多智能体系统,其每个跟随智能体的状态方程为

则称系统(2)和(3)关于前l个分量达到部分分量一致。

当l取n时,定义4中的部分分量一致就变成了多智能体的所有分量一致,即多智能体恒同一致属于部分分量一致的特殊情形,部分分量一致是更普遍的动力学行为。

定理1 若系统(2)和(3)可使假设1成立,且满足

将V沿系统(9)的轨迹对t求导,可得:

则当t→+∞时,^e q(t)→0,q=1,2,…,l,即偏差系统(9)前l个分量收敛到零。综上可知,在自适应牵制控制(4)下,系统(2)和(3)可实现领导-跟随部分分量一致。

3 数值模拟

例1 设该系统是由1个领导者和4个跟随智能体组成,领导者的信息只能传给第2个跟随智能体(根节点),其中第i个智能体的动力学方程[13]为

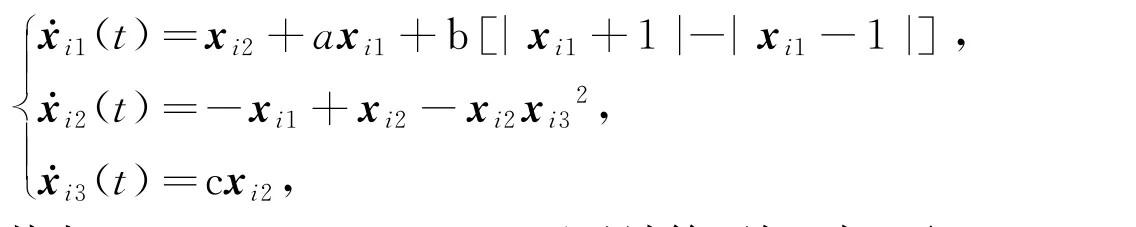
其中a=-3,b=2,c=2。通过计算可知,当ε取1时,假设1成立。

多智能体的拓扑图含有一个生成树,如图1所示。

图1 拓扑图

根据图1可取Laplace矩阵L和B分别为:

令Γ=diag(1,1,0),选取自适应更新率为式(10),经计算可得λmin(D^)=0.191,若要满足定理1中的条件,则可取ε=1,α=1,h*=9。

利用MATLAB软件进行计算,得到误差演化曲线如图2所示。从图2可看出,智能体的前2个分量分别实现一致,而最后一个分量并未最终收敛到零,即未达成一致。不同牵制控制b2=1,2,3.5,4.1所对应的自适应增益H(t)的轨迹如图3所示。从图3可看出,自适应增益最终趋于某个定值即有界。综上所述,系统(2)和(3)在控制器(4)下可实现前2个分量一致。

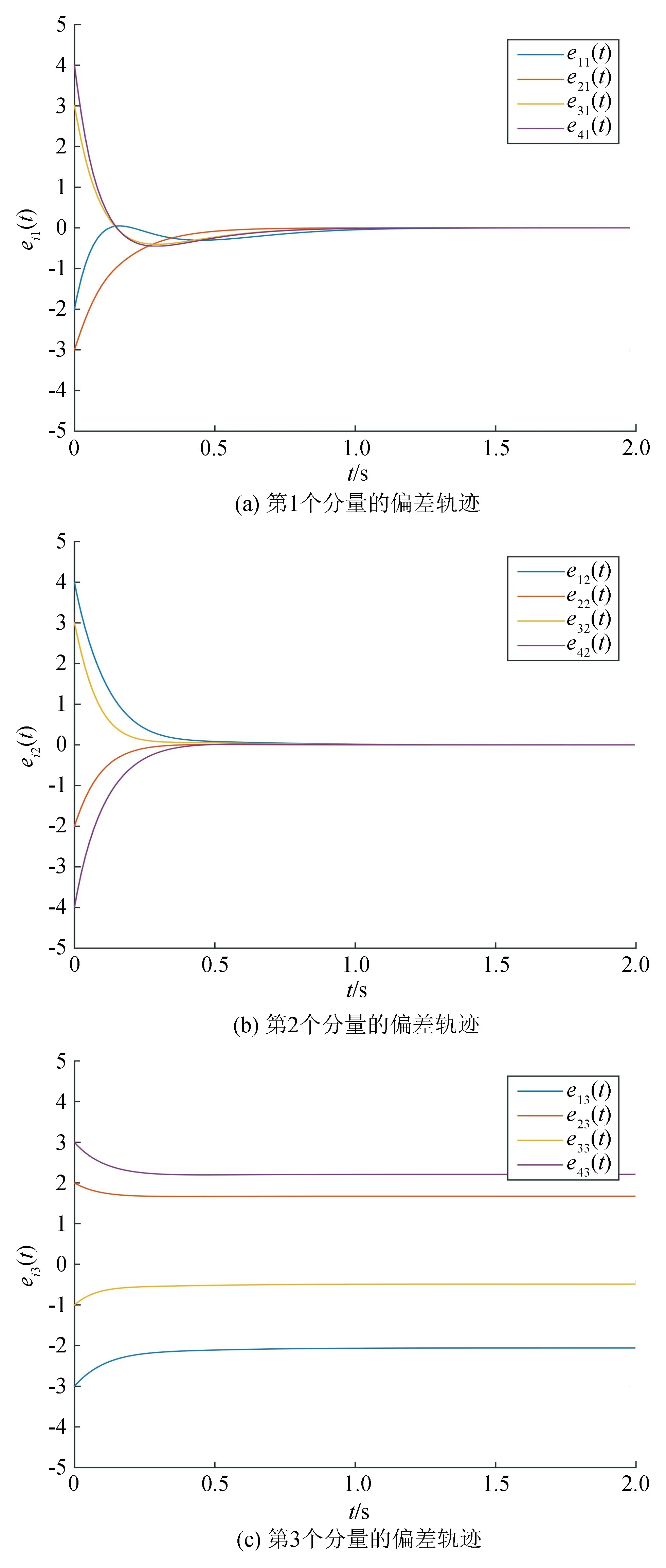
图2 跟随者与领导者的状态误差演化曲线

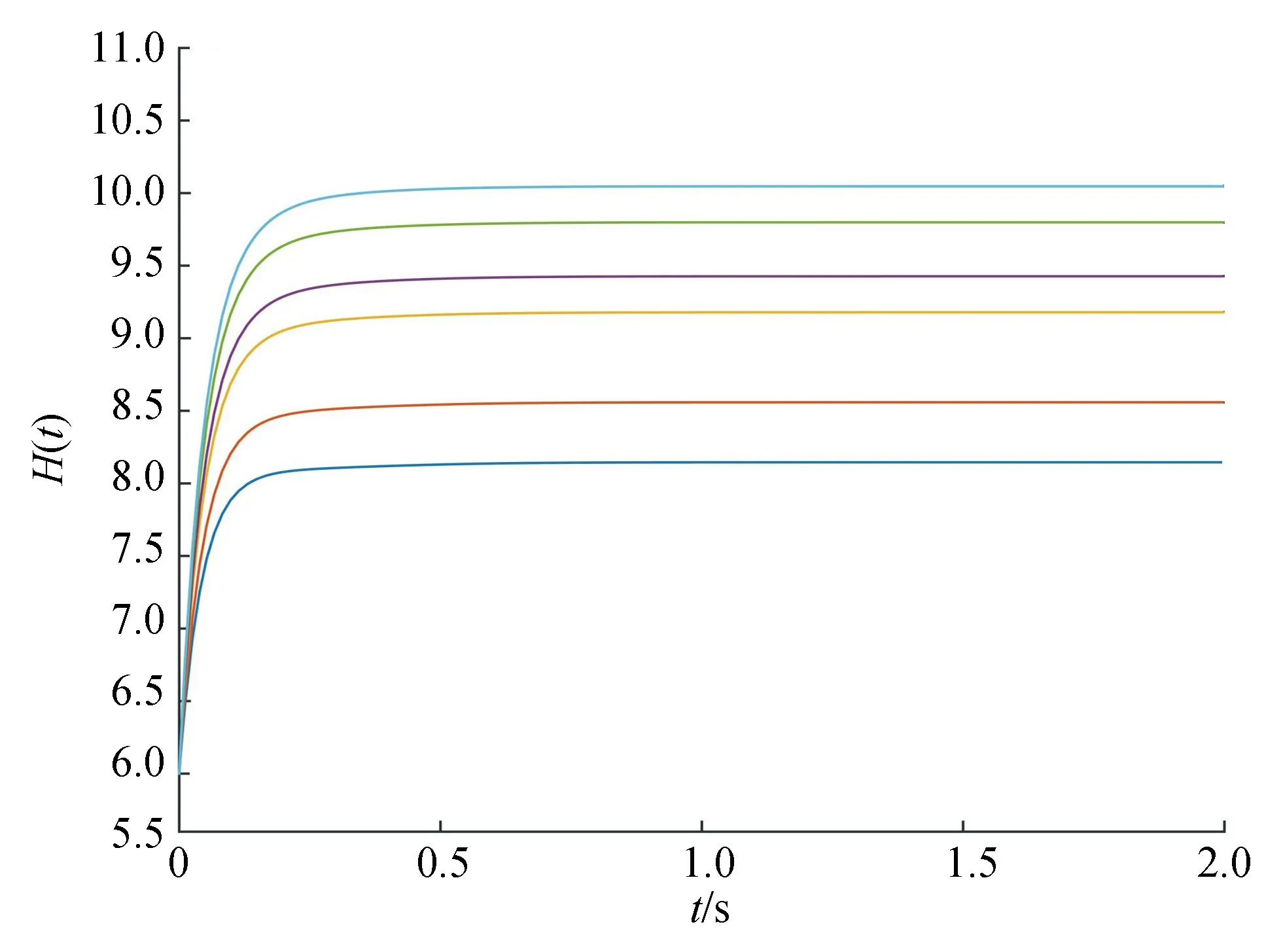
图3 不同牵制控制所对应的自适应增益的轨迹

4 结束语

利用自适应牵制控制器探究了一阶领导-跟随系统的部分分量一致性问题,将原有的偏差系统转换为新的偏差系统,以分析多智能体的部分变元指数稳定性,最终获得了一些充分条件。此外,验证了只需牵制少量关键节点即可确保系统达到部分分量一致。目前,将自适应牵制控制方案应用到二阶或高阶系统的部分分量一致性问题的研究还未曾涉及,之后会在这方面进行研究。