一种求解线性圆锥互补问题的非精确光滑牛顿法

2021-12-14韦洪锦迟晓妮黄鸿柳李春红

桂林电子科技大学学报 2021年3期

关键词：二阶方程组圆锥

韦洪锦, 迟晓妮, 黄鸿柳, 李春红

(1.广西科技师范学院数学与计算机科学学院,广西来宾 546100;2.桂林电子科技大学数学与计算科学学院,广西桂林 541004)

一般线性圆锥互补问题(LCCCP)[1]是指求一向量x∈Rn,使得

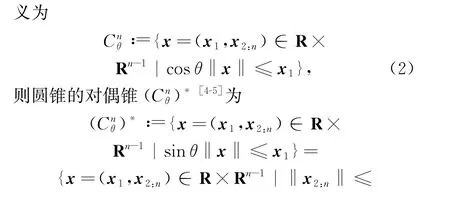
其中:θ∈(0,π/2)为给定的旋转角;‖·‖为欧几里得范数。故当θ≠π/4时,圆锥是非自对偶的,因此其是非对称锥。而当θ=π/4时,n-维圆锥化为n-维二阶锥[6],即

则问题(1)转化为线性二阶锥互补问题(LSOCCP)[7]。

为方便起见,用x=(x1,x2:n)∈R×Rn-1表示x=(x1,x2:nT)T,用(x,s)表示(xT,sT)T。

LCCCP被广泛应用于工程问题,如四足机器人力优化问题和多指手臂机器人的抓力操作问题等[8-9],同时其又是非对称锥互补问题的特例,因此近年来备受关注[1]。目前有很多求解互补问题的算法,如内点算法[10-11]、半光滑牛顿法、光滑牛顿法[12-13]等。因其具有较好的理论结果和数值效果,光滑牛顿法被推广到很多领域,如二阶锥优化问题[14-15]和圆锥规划问题[16-17]等。此外,光滑牛顿法不要求初始点和中间迭代点的严格可行性,且一般具有全局和局部二阶收敛性,因此是求解LCCCP的一种好方法,其主要思想是将LCCCP转化为与之等价的方程组,然后运用光滑技术求解该方程组,从而得到LCCCP 的解。但在求解规模较大的问题时,在每次迭代中精确地求解方程组往往效率不高。因此,考虑使用非精确牛顿法[12,18]近似地求解方程组,以提高算法的效率。

基于一个新的圆锥互补函数的光滑函数,提出一种求解LCCCP的非精确光滑牛顿法。该算法在每次迭代中运用非精确牛顿法近似地求解方程组,以减少计算量。在较弱的条件下,证明了算法具有全局和局部二阶收敛性。数值结果表明,该算法可求解LCCCP。

1 预备知识

以下给出与二阶锥[6]相伴的欧几里得Jordan代数的概念。

对任意x=(x1,x2:n)∈R×Rn-1和s=(s1,s2:n)∈R×Rn-1,定义Jordan内积

2 算法及其收敛性

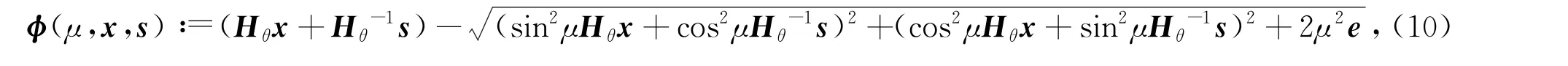
其中μ≥0是一个实参数,θ∈(0,π/2)。当θ=π/4时,ϕ(μ,x,s)退化为一个二阶锥互补函数的光滑函数[14]。以下定理给出该函数的性质。

定理1 设函数ϕ:R+×Rn×Rn→Rn由式(10)定义,则:

1)ϕ(0,x,s)=0⇔x∈Cnθ,s∈(Cnθ)*,=0;

2) 对任意(μ,x,s)∈R++×Rn×Rn,ϕ(μ,x,s)连续可微,且其雅可比为

由定理1得Φ(z)=0⇔μ=0和(x,s)是LCCCP的解。因此,基于函数ϕ(μ,x,s),当μ>0时,可在每步迭代中使用非精确光滑牛顿法求解方程组Φ(z)=0。令μ→0,得LCCCP的解(x*,s*)。

定理2 设M是半正定矩阵,且函数Φ(z)由(12)定义,则:

1) 对任意z=(μ,x,s)∈R++×Rn×Rn,Φ(z)连续可微,且其雅可比矩阵为

算法1 求解LCCCP的非精确光滑牛顿法

定理3 设M为半正定矩阵,且{z k=(μk,x k,s k)}是算法1生成的迭代序列, 则算法1适定,且对任意k≥0,有μk∈R++。

证明由于μk>0,且M为半正定矩阵,故由定理1知,Φ'(z)可逆,从而步骤2)适定。下证存在λ-∈(0,1),使任意λ∈(0,λ-]满足式(24)。令Δz k∶=(Δμk,Δx k,Δs k)是(23)的唯一解,则

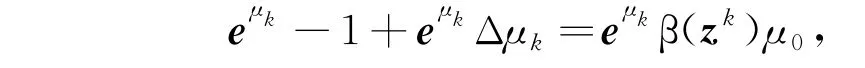
又由引理1得

因此,对任意λ∈(0,1),有

对任意λ∈(0,1),定义

由β(z k)的定义,当Ψ(z k)<1时,

定理4 若M是半正定矩阵,则算法1产生有界无穷序列,且任一聚点都是方程Ψ(z)=0的解。

证明用数学归纳法证明。易见z0∈Ω。假设z k∈Ω,即μk≥β(z k)μ0。由式(25)和β(z k)的定义有

故z k∈Ω。

其中λ-∈(0,1],η-∈[0,1-2γμ0]。因此,对任一非负整数l满足δl∈(0,λ-],

又因为对充分大的k有λk=δl k≥δl,故由式(24)和(30)得

对上式两边取极限有

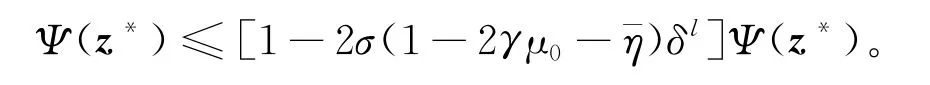
从而Ψ(z*)≤0,这与假设矛盾,因而z*是方程Ψ(z)=0的解。

类似定理8[21]的证明,有以下定理。

定理5 若M是半正定矩阵,z*为算法1产生的迭代序列{z k}的一个聚点。如果所有V∈Φ(z*)(∂Φ(z*)为函数Φ(z)在z*处的Clarke[22]意义下的广义雅可比)非奇异,那么{z k}局部二阶收敛到z*,即

‖z k+1-z*‖=O(‖z k-z*‖2),且μk+1=O(μk2)。

3 数值结果

运用MATLAB (R2016a)在配置为2.11 GHz CPU 处理器、8.00 GiB内存的个人计算机上进行数值实验。

算法1中选择以下参数:μ0=0.1,δ=0.95,σ=0.2,γ=0.45,ηk=2-k。以Ψ(z k)<ε=10-8作为终止准则。Iter和CPU 分别表示迭代次数和计算时间,n是维数。随机生成一个向量q=rand(n,1)和矩阵A=rand(n,n),M=ATA,其中A和q中的元素是[0,1]随机产生的数。令x0=e,s0=0为初始点。针对不同旋转角和不同规模LCCCP进行求解,结果如表1和表2。