基于NVD的半圆式钢桁梁异型斜拉桥抗震性能分析

陈爱军，周 彦，贺国京

(中南林业科技大学 土木工程学院，湖南 长沙 410004)

近年来，随着建筑结构抗震设计由“基于强度的结构抗震设防理念”逐步转变为“基于性能的结构抗震设计思想”，桥梁结构的耗能减震技术也在理论研究与工程应用方面获得了长足发展[1-4]。毋庸置疑，NVD作为一种高效且稳定的耗能减震装置，不仅可以显著地降低桥梁结构或结构构件在正常使用荷载以及地震荷载激励下的位移响应，保证桥梁结构正常使用的安全性，还能够集中耗散地震能量，减轻结构体系的损伤程度，而且它的可替换性也直接增强了桥梁结构震后功能的可恢复性[5-6]。因此，NVD在提高桥梁结构抗震性能方面备受青睐。

关于NVD在桥梁结构中的应用方面，国内外学者做了一系列的研究。其中，Jin Zhu等[7]基于简化的Maxwell模型，探讨了线性粘滞阻尼器与NVD应用于斜拉桥抗震中的差异性；Li Xu等[8]通过代数公式拟合了阻尼设计变量与结构位移响应变量之间的关系，从而有效地确定了粘滞阻尼器的最优参数；黎璟等[9]对不同设防烈度下的多组减震方案进行了比较，并提出了相关参数优化原则。梁冠亭[10]与肖开乾[11]等分别以大跨度斜拉桥、拱桥为研究对象，探讨了地震荷载激励下NVD的实用性能。

在大量的理论研究与工程应用的支撑下，NVD的产品种类与实用性能日趋多样性与高效性，而其在桥梁结构的抗御地震设计当中也得到了广泛的应用。因此，文中采用ANSYS有限元计算软件，选取了结构位移响应与跨中弯矩响应为主要的特征点，定量地分析了NVD的特征参数与布设方案对一座半圆式钢桁梁异型斜拉桥抗震性能的影响。同时，通过抗震随机分析，进一步探讨了该类型桥梁结构在地震荷载的随机激励下，NVD对结构位移响应的影响，为异型斜拉桥的抗震分析与减震设计提供参考。

1 有限元计算模型的建立

1.1 工程概况

雪峰山景区大峡谷西侧悬崖峭壁上一座景观人行桥为半圆式钢桁梁异型斜拉桥，主梁采用平面为半圆的钢桁梁，长49.6 m，宽1.62 m，内弧半径为15 m；全桥11根长度均为21.1 m的斜拉索采用等间距的布置形式，其一端锚固于内侧上弦杆，另一端则通过锚座悬挂于岩壁上，如图1所示。钢桁梁由Q345qD钢材制成的方形钢管焊接成，梁端各设3个附岩支座，并与锚固于山体内部的锚杆铰接；桥面铺设轻质松木板。

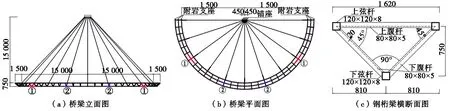
图1 桥梁总体布置图(单位：mm)Fig.1 Overall layout of the bridge(Unite:mm)

1.2 空间有限元计算模型

此次分析采用ANSYS建立三维有限元仿真模型，如图2所示。其中， 采用Beam188空间梁单元、 Link180

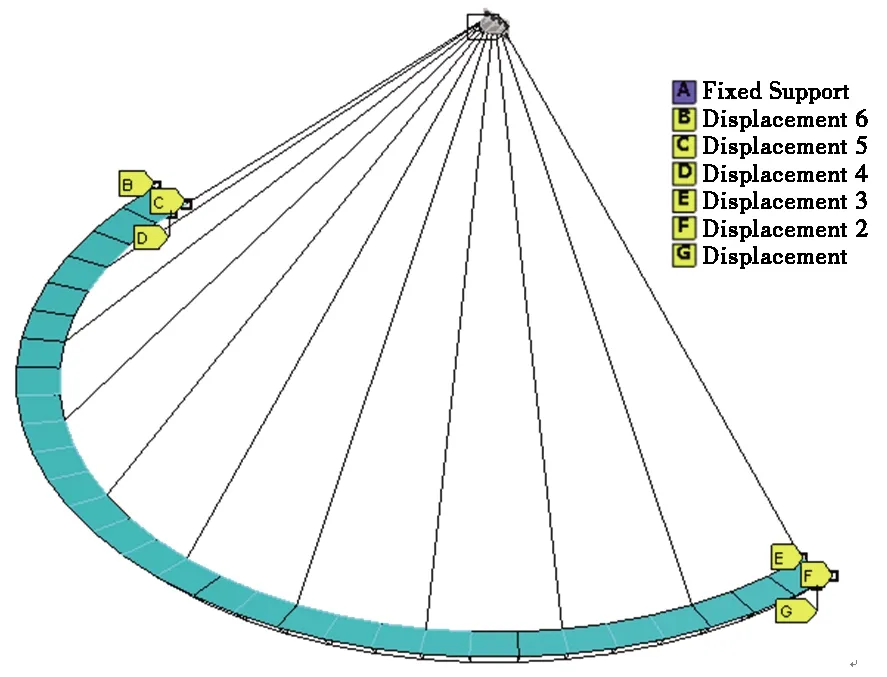
图2 有限元模型Fig.2 Finite element model

空间杆单元、Solid45空间实体单元以及Shell181空间壳单元分别模拟钢桁梁、拉索、锚座与桥面板。另外，钢桁梁梁端与锚杆之间、斜拉索与钢桁梁之间以及斜拉索与锚座之间均采用铰接连接；而锚座与岩体之间采用固结连接。

考虑到几何非线性与材料非线性对桥梁抗震性能的影响，通过Ernst公式修正拉索的弹性模量，并计入桥梁结构的大变形效应。其中，钢材作为一种各向同性材料，可采用理想弹塑性本构模型实现钢桁梁、拉索以及锚座的材料非线性，而松木板则采用正交各项异性弹塑性本构模型与等向强化本构模型来模拟其相应的非线性力学行为。各构件的材性参数如表1所示。

表1 基本材性参数Table 1 Value-taking for material properties

2 半圆式钢桁梁异型斜拉桥桥动力特性分析

为研究该桥的固有频率以及振型特点，采用瑞利-李兹向量法对斜拉桥进行了模态分析，算得成桥状态下前10阶的主振型。其中，该桥前4阶主振型与相应的振型特性参数分别如图3与表2所示。

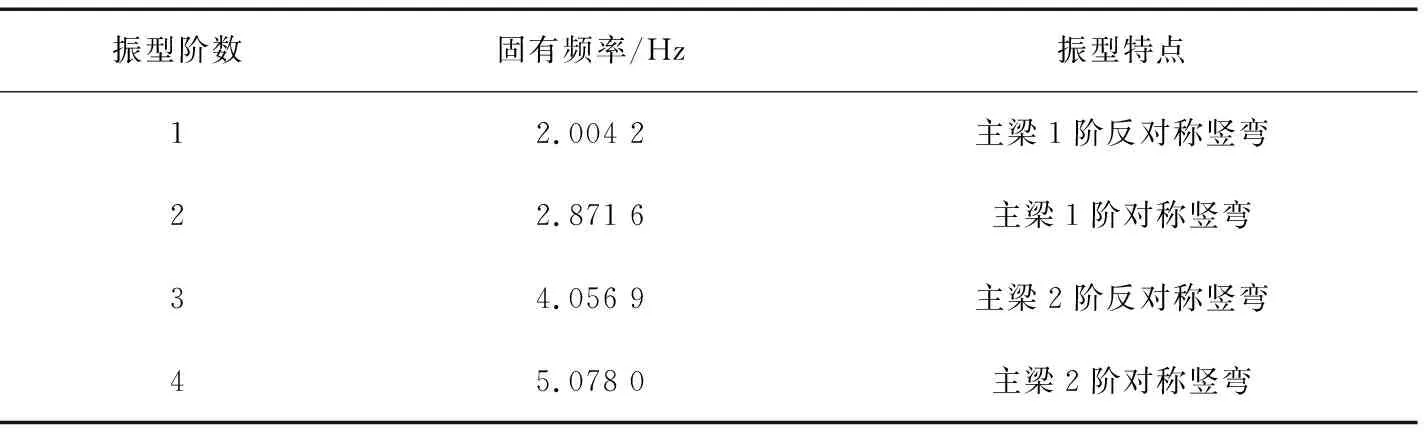
表2 模态分析结果Table 2 Results of modal analysis

3 含NVD的振动微分方程

虽然ANSYS有限元软件当中既有的Combin单元通过相应的参数设定能够准确模拟弹簧-阻尼器的动力特性，但是只有Combin37单元所具有的非线性行为能完美地契合NVD(速度型)的力学模型[12]。其力学模型[13]如式(1)所示。

FD=Cv·Vλ·sgn(V).

(1)

式中：FD、V分别为阻尼力与相对速度；Cv、λ均为粘滞阻尼器的基本参数，分别表示阻尼系数与速度指数。其中，λ的取值区间通常为0.3≤λ<1.0，FD输出为非线性阻尼力；当λ取值为1.0时，FD输出为线性阻尼力；当λ取值为0时，FD输出为摩擦阻尼力。

对于含有NVD的ANSYS有限元计算模型，仅在地震荷载激励下的振动微分方程可表示为：

Mu″(t)+Cv·u′(t)λ·sgn[u′(t)]+Cu′(t)+K·u(t)=-Mag(t).

(2)

式中：M、C与K分别表示有限元模型的质量矩阵、阻尼矩阵与结构刚度矩阵；u″(t)、u′(t)与u(t)分别表示地震荷载激励下的加速度响应列向量、速度响应列向量以及位移响应列向量；ag(t)为地面运动加速度列向量。

而在ANSYS有限元软件当中，上述振动微分方程通常可以采用Newmark-β法对其进行迭代求解[14-17]，其基本方程为：

(3)

式中：β与Δt均为积分控制参数，限定了时间增量内的加速度变化规律。其中，当β≥0.25时，Newmark-β法可以保证无条件收敛；当0.25≥β≥0时，Newmark-β法有条件收敛；另外，Δt的取值通常受限于结构的固有频率以及荷载步长。

4 NVD的参数敏感性分析

上述斜拉桥的模态分析结果表明，自由振动下该桥的位移响应主要表现为主梁的竖向弯曲变形，并且前四阶主振型的位移响应主要集中于钢桁梁的1/5跨与4/5跨、2/5跨与3/5跨以及跨中，因此可在相应的位置布设NVD，并以阻尼系数与速度指数两项参数为控制变量，以地震荷载激励下结构位移响应与跨中弯矩响应为特征点，探讨不同布设方案下NVD的参数敏感性问题。

4.1 地震波的选取

由桥规[18]以及工程场地的《安评报告》可知，该桥属于B类桥梁，特征周期为0.35s，场地类型为Ⅱ类，再结合抗震设防要求，设计该桥的加速度反应谱，得到了与之匹配度较高的1条天然地震波(El Centro波)与3条E2级人工地震波，用于NVD的参数敏感性分析[19]。其相应的加速度反应谱如图4所示。

图4 加速度反应谱Fig.4 Acceleration response spectra

4.2 NVD布设方案以及参数敏感性分析

合理的布置形式能够充分发挥出NVD的减震性能与耗能性能，从而降低桥梁主体结构在地震荷载作用下位移响应以及非线性的程度，延缓桥梁结构塑性铰的产生与发展[20]。因此，根据上述动力特性分析结果，可将NVD布设于钢桁梁产生位移响应峰值的部位，即钢桁梁的1/5跨和4/5跨(方案1)、2/5跨和3/5跨(方案2)，具体布设位置如图1所示。图中的①与②分别为方案1、方案2所对应的NVD布设位置，每一布设位置均设有沿钢桁梁下弦杆轴向布置的2个阻尼器(对称布置)以及沿钢桁梁下腹杆轴向布置的2个阻尼器(对称布置)。

另外，为研究不同阻尼系数Cv与速度指数λ的NVD对该斜拉桥抗震性能的影响，文中通过ANSYS有限元软件，分别计算了不同参数组合下的NVD对该斜拉桥抗震性能的影响，其中Cv取值为300、400、500、600、700 kN/(m·s-1)λ，λ取值为0.3、0.4、0.5、0.6、0.7、0.8、0.9，具体如表3所示。

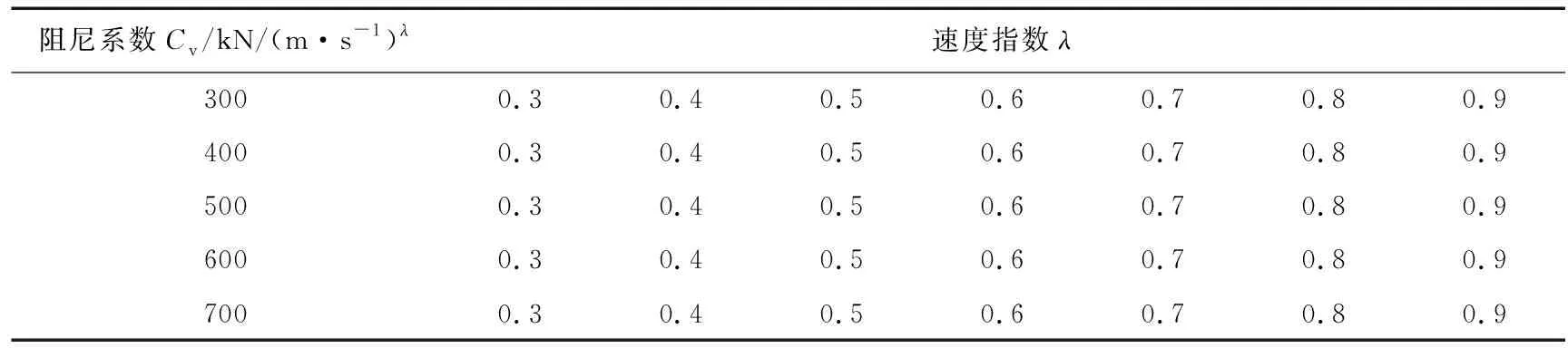
表3 阻尼系数与速度指数的不同组合Table 3 Different combination of damping coefficient and velocity exponent

基于上述2种不同减震方案的设控模型与不设阻尼器的基准模型，通过ANSYS有限元软件当中的瞬态动力学分析模块，对设控模型与基准模型分别施加相应的地震荷载，并采用Newmark-β法对结构体系的运动微分方程进行求解。其中，考虑到Newmark-β法本质上属于2阶精度的求解方法，且当积分控制参数β取值为0.25时，满足无条件稳定的Newmark-β法仍能确保2阶的计算精度，因此积分控制参数β可取值为0.25；另外，文中提取的最高阶自振模态(固有频率为16.846 Hz)对结构整体的响应仍有贡献，故时间步长Δt的取值应小于0.002 9 s，且当地震荷载步长(0.02 s)为Δt的整数倍时，计算结果更为精确，因此Δt宜取为0.002 s。

由非线性时程分析算得斜拉桥分别在E2-1、E2-2、E2-3三条人工地震波激励下的跨中最大位移响应均值与跨中最大弯矩响应均值、以及El Centro天然地震波激励下的跨中最大弯矩响应与跨中弯矩响应，具体如图5、图6所示。由图5与图6可知，当地震荷载为人工地震波时，方案1与方案2的跨中最大位移响应均值的折减范围分别为9.74%～56.05%和5.81%～47.39%，跨中最大弯矩响应均值的折减范围则为33.86%～41.92%和20.61%～29.87%；而当地震荷载为天然波时，方案1与方案2的跨中最大位移响应值的折减范围分别为13.31%～51.76%与10.53%～44.45%，跨中最大弯矩响应值的折减范围则为34.51%～52.23%与25.19%～43.89%。

图5 人工波激励下的地震响应Fig.5 Seismic response excitated by artificial waves

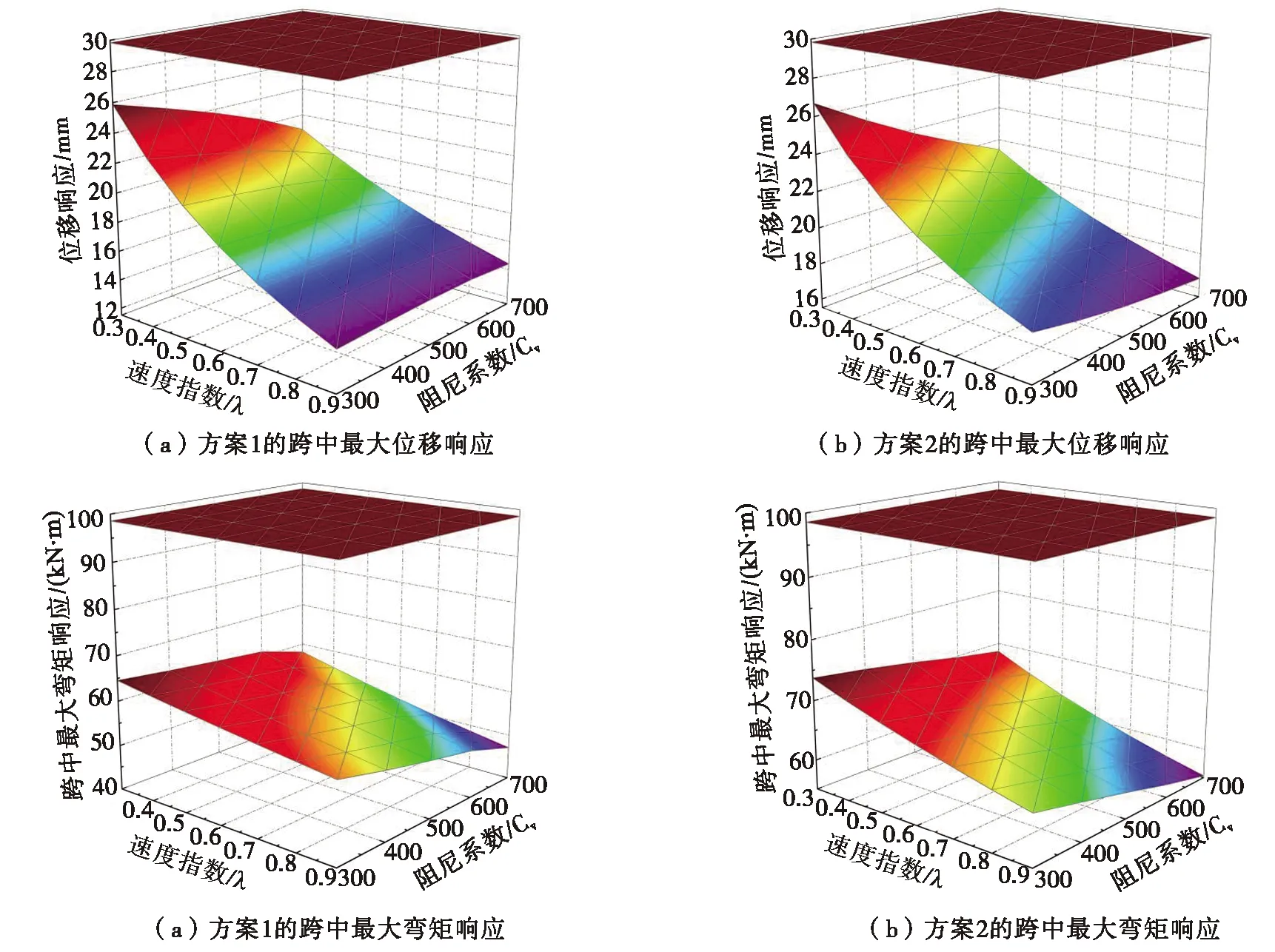
图6 天然波激励下的地震响应Fig.6 Seismic response excitated by natural wave

就总体而言，采用不同减震方法的优化模型所产生的地震响应相较于基准模型均有不同程度的折减，但方案1的折减程度则明显大于方案2，且其折减趋势均与速度指数λ、阻尼系数Cv呈正相关。另外，计算结果的变化规律显示，在上述取值范围内单一变化的速度指数λ和阻尼系数Cv对计算结果的影响程度也有不同，主要表现为结构的位移响应对速度指数λ的敏感程度要显著高于阻尼系数Cv，因此仅从抗震性能的角度考虑，可优先选用速度指数较高的阻尼器应用于该类型斜拉桥。

5 半圆式钢桁梁异型斜拉桥抗震随机分析

桥梁结构传统的抗震分析方法往往是将地震荷载视作一种与时间密切相关的动力荷载，具有较高的一般性与确定性。然而，现实当中的地震荷载作用于桥梁结构的开始至结束，其本身就是一个非常复杂的物理过程，具有较高的随机性与不确定性，而将这一物理过程视为一个随机的过程并通过随机振动法来研究桥梁结构的抗震性能才具有较高的适用性与合理性。因此，文中基于ANSYS有限元软件当中的随机振动模块，对该斜拉桥进行抗震随机分析，并采用上述方案1的布设形式，探讨随机振动激励下NVD的减震性能。其中，参考文献[21]可计算得到与上述设计反应谱等效的地震加速度功率谱，用于该斜拉桥的抗震随机分析，其功率谱如图7所示。

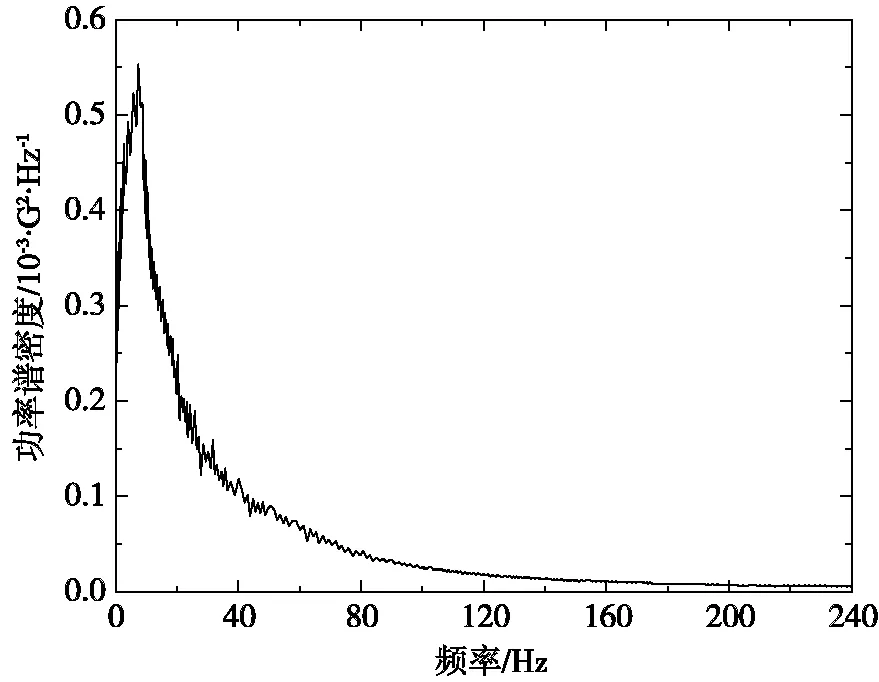
图7 地震加速度功率谱Fig.7 Seismic acceleration power spectrum

在模态分析的基础之上，引入随机振动分析模块，并分别在X、Y和Z三个方向上载入如图7所示的地震加速度功率谱，对该斜拉桥进行随机地震响应分析，分别得到设控模型与基准模型的位移响应云图，且该桥各处所产生的位移响应Δ满足高斯正态分布Δ～N(μ，σ2)，而68.269%的位移响应Δ处于均值μ一个标准差σ的区间之内。计算结果表明：虽然设控模型的位移响应均要低于基准模型，且设控模型的位移响应变化规律与时程分析结果基本一致，但当NVD的速度指数λ的取值大于0.7、阻尼系数Cv的取值大于500时，其减震率的增幅开始随速度指数λ与阻尼系数Cv的增大而逐渐开始降低，因此仅以该组参数组合下的设控模型为例，分析其减震性能。

由图8可知，地震荷载激励下钢桁梁位移响应峰值出现于钢桁梁的1/5跨和4/5跨，且该值不超过26.19 mm的概率为68.269%。然而根据方案1，在钢桁梁的1/5跨与4/5跨布设相应的NVD之后，该两处位置的位移响应数值得到了明显的控制，主要表征为大概率下的位移响应峰值将降至13.42 mm，减震效果显著。

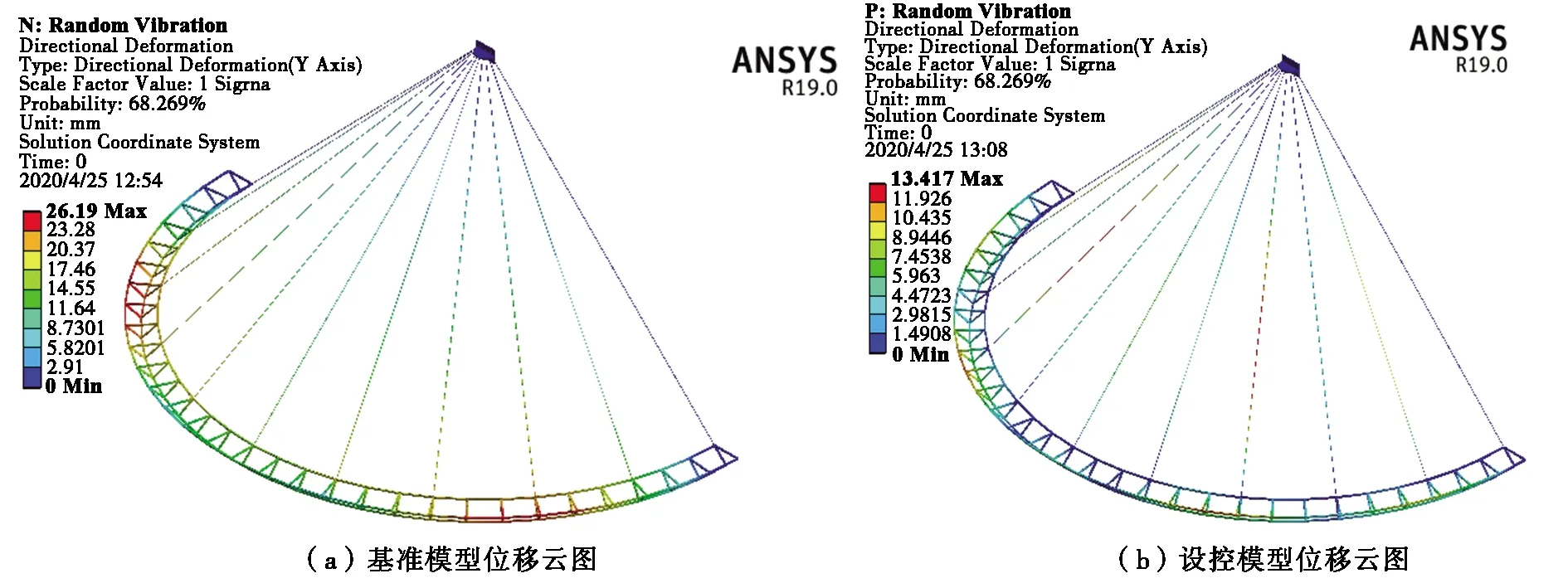
图8 位移云图对比结果Fig.8 Comparison results of displacement nephograms

6 结论

针对一座半圆式钢桁梁异型斜拉桥，以ANSYS有限元软件为主要工具，探讨了NVD的参数设定以及布设位置对该类型桥梁结构抗震性能的影响，得出的结论如下：

(1)在钢桁梁的下弦杆、腹杆处布设相应的NVD之后，桥梁结构在地震荷载激励下的位移响应与弯矩响应得到了有效的控制。且单从最大位移响应均值与最大弯矩响应均值的折减程度来看，方案1要明显优于方案2。

(2)NVD的参数敏感性分析显示：结构最大位移响应均值与跨中最大弯矩响应均值的折减程度与阻尼器参数的大小呈正相关，且在拟定范围内单一变化的前提条件下，结构的位移响应对速度指数λ的敏感程度要明显高于阻尼系数Cv，因此可权衡阻尼器的造价、预计的减震效果等因素，优先选用速度指数较高的阻尼器应用于该类型斜拉桥。

(3)在斜拉桥抗震随机分析之中，设控模型的位移响应峰值相比于基准模型降低48.76%，并且设控模型的位移响应均得到了明显的控制，从而保证了桥梁结构易损部位的安全性，也在一定程度上反映了方案1的合理性与高效性。