基于相位差法和多重滤波法结合的瑞雷面波频散曲线研究

2021-12-13熊章强张大洲

工程地球物理学报 2021年6期

谌强，熊章强,2，张大洲,2

(1.中南大学地球科学与信息物理学院，湖南长沙 410083；.中南大学有色金属成矿预测与地质环境监测教育部重点实验室，湖南长沙 410083)

1 引言

瑞雷面波法作为一种工程勘察手段，由于具有抗干扰能力强、垂向分辨率高和野外数据采集相对简便等优点广泛应用于浅层地质勘查、地质灾害调查和无损检测等方面[1-3]。瑞雷面波勘探中频散曲线提取是非常关键的一个环节，其提取的正确与否直接关系到最终反演结果的可靠程度，因此如何准确提取频散曲线对于瑞雷面波勘探显得尤为重要。目前在瑞雷面波勘探频散曲线提取中大多采用多道瞬态面波分析法(Multi-channel Analaysis of Surface Wave，简称MASW)[4]，这种面波分析方法利用多道叠加效应能够得到较为准确的频散曲线，因而在垂向上探测精度较高。但由于多道叠加效应，一般在工程上应用12道或24道得到的地震记录只能计算出一条频散曲线，这样使得MASW方法由于其平均效应导致在横向上分辨率相对较低，因此只能适用于介质速度横向变化比较小的地层探测。为了提高MASW方法的横向分辨率，Koichi Hayashi等人[5]提出并借鉴了地震反射波勘探中共反射点多次覆盖思想的共中心点(Common Mid-Point,CMP)瞬态多道面波方法，该方法利用密集的多覆盖数据能获得相对于常规瞬态面波方法更密集的频散曲线，从而提高横向分辨率。胡晋等人[6]通过CMP解析法再利用相位差法提取频散提高了频散曲线的精度。但对于共中心点叠加数据，当炮检距较大时，所获得的地层的频散信息也会同样存在平均效应。

随着瑞雷面波应用范围的不断扩大和需要解决的地质问题复杂程度的增大，对于探测如孤石、岩溶及城市塌陷等地质异常体时需要有较高的横向分辨率[7-9]，在这种情况下，MASW方法往往得不到较好的效果。面波谱分析法(Spectral Analysis of Surface Wave，简称SASW)是通过计算不同频率下的两道信号相位差，得到该频率下的相速度[10]。相较于MASW法，利用SASW方法对于一个单炮记录可提取多条频散曲线，显然可以提高瑞雷面波探测的横向分辨率[11]。利用两道地震数据提取频散曲线的方法除SASW外，多重滤波法也是一种常用方法，该方法避免了利用两道信号相位差计算相速度时相位的不稳定性以及相位差需要小于2π的要求。Xiao-Ping Li等人[12]详细介绍了多重滤波方法的基本原理。周青云等人[13]证明了多重滤波法在分析面波的频散特性是一种有效而快速的方法，并研究了多重滤波法的可靠性。陈杰等人[14]利用多重滤波法提取了基阶和高阶瑞雷面波频散曲线。

在瑞雷面波法勘探中，理想的情况是尽可能利用少的地震道数据提取到较为可靠的频散曲线，这样既能够满足垂向探测的需求，在横向上也有较高的分辨率，达到能准确探测地下地质结构的目的[15,16]。但由于目前采用的是瞬态瑞雷面波勘探方法，震源在激发后会产生不同频率、不同模式的面波信号，这些不同类型叠加的信号在利用两道数据提取频散曲线时会互相影响，导致所得到的频散曲线产生较大误差[17]，这也是目前采用多道数据来计算频散曲线的一个重要原因，即通过多道数据累加来增强频散曲线的准确性和稳定性。两道数据计算频散曲线的相位差法是通过计算两道的相位差得到不同频率的相速度，而多重滤波法是通过求得两道数据不同频率信号的时间差来计算其相速度。

本文通过对原始地震数据进行模式分离，然后对分离后的两道数据分别利用相位差法和多重滤波法计算出相速度后进行叠加，提高了频散曲线的可靠性，并通过理论模型和实测数据说明了该方法的有效性。

2 基本原理

2.1 相位差法

假设地面x1,x2两点处地震记录分别为u1(t),u2(t)，其中x2-x1≤λR，λR为瑞雷波波长(m)，则x1,x2两点处瑞雷面波的垂直位移方程可分别简写为：

(1)

(2)

式中，A1和A2分别为两点的幅值(m);t为时间(s);w为角频率(rad/s);VR为相速度(m/s)。则可得它们之间的相关系数可写为：

(3)

式中，τ为u1(t)与u2(t)之间的延迟时间(s);T为延迟最大时间(s);对求出的相关系数进行傅里叶变换，可得：

(4)

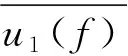
(5)

式中，Δx为两点距离差(m);通过公式(5)可计算出不同频率下瑞雷面波的相速度VR。

2.2 多重滤波法

多重滤波法将两道地震数据通过窄带滤波，利用两道信号之间某一频率下的能量极值对应的时间差来计算相速度。具体在计算时，先分别对两道地震信号S(t1)和S(t2)进行傅里叶变换至频率域：

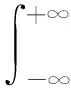
(6)

式中,f为频率(Hz);t为时间(s)。接着设计带通滤波器H(wn,w)如公式(7)所示：

(7)

式中,fn为中心频率(Hz);f1n为上限频率(Hz)，在本文中取0.75fn;f2n为下限频率(Hz)，取1.25fn;α为衰减因子，取50.3。在获得频率域信号u(f)和滤波器H(fn,f)后将两者相乘再做傅里叶反变换到时间域，如式(8)所示：

(8)

再对式(8)进行希尔伯特变换得到式(9)：

(9)

最后对其求幅值：

(10)

式中,real表示取复数的实部。对于两道数据通过窄带滤波得到单频信号的幅值An后，分别可以得到两道记录能量最大值A1和A2所对应的时间t1和t2，进而计算出时间差Δt。利用公式V=Δx/Δt便可以求出对应频率的速度值，式中Δx为两道之间的距离(m)。

两道数据分别利用相位差法和多重滤波方法计算出不同频率对应的相速度值。为了能够实现将两种不同方法计算得到的结果进行叠加，同时将不同道间距及不同震源位置多次激发地震波所计算得到的结果进行累加，本文通过将给定的一个速度范围值再根据速度间隔进行离散化，形成一个F-V的二维数组，对于不同频率计算得到的速度值找到对应的数组并在其中赋值为1，从而形成一个频散谱。对于不同方法、不同道间距及不同炮点所计算的频散谱进行叠加，最后在频率方向上做归一化，这样就形成了最终的频散谱，然后从频散谱中的不同频率值拾取能量最大位置所对应的速度值就能得到频散曲线。

3 理论模型测试

3.1 两层层状介质模型

为了对比分析相位差法和多重滤波法相结合计算频散曲线的有效性，特设计一个两层层状介质模型，模型大小为100 m×50 m。第一层厚度H1=10 m,纵波速度为VP=800 m/s，横波速度VS=200 m/s，密度ρ=2.0 g/cm3；第二层纵波速度VP=1 200 m/s，横波速度VS=400 m/s，密度ρ=2.0 g/cm3。采用高精度交错网格有限差分法对该模型进行全波场正演模拟[18,19]，震源为主频20 Hz的雷克子波，位于地表(0,0)处。模拟得到的地震记录如图1所示，地震记录共90道(绘图时以2 m道间距绘制)，道间距为1 m，偏移距10 m，采样间隔为0.20 ms，采样点数为5 001。

从图1中可以清晰地看出,模拟得到的地震记录中有反射波、直达波、折射波和面波等，其中瑞雷面波能量最强，同相轴最明显。为验证将相位差法和多重滤波方法结合的有效性，分别对原始地震记录以及F-K模式分离后的地震记录进行处理。首先取原始地震记录的第44道和第46道用相位差法和多重滤波方法分别计算其频散谱，如图2所示。图2(a)为利用相位差法计算得到的频散谱，从图中可以看出通过计算得到的相速度值与理论值部分能够对应，但在20～60 Hz段误差相对较大，最大误差达10 %。存在误差的主要原因应是各模态面波信号之间的相互影响所致。张大洲等人[20,21]通过模式分离方法也对此进行过同样的分析。图2(b)为利用多重滤波法计算得到的频散谱，与通过相位差法计算的结果相比较，其误差相对较小，最大误差为8 %。从图2(a)和图2(b)的结果对比来看，利用多重滤波方法计算频散曲线时各模式之间的影响相对较小。将两种方法计算得到的频散谱进行叠加得到如图2(c)所示结果，从图中可以看出，将两种方法计算得到的频散谱进行叠加后其相速度相同的位置所对应的能量就会有所加强，从而使得计算结果更加稳定。

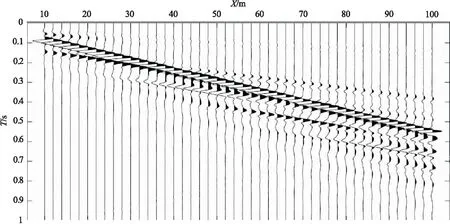
图1 两层模型原始地震记录Fig.1 Original seismic record of two-layer model

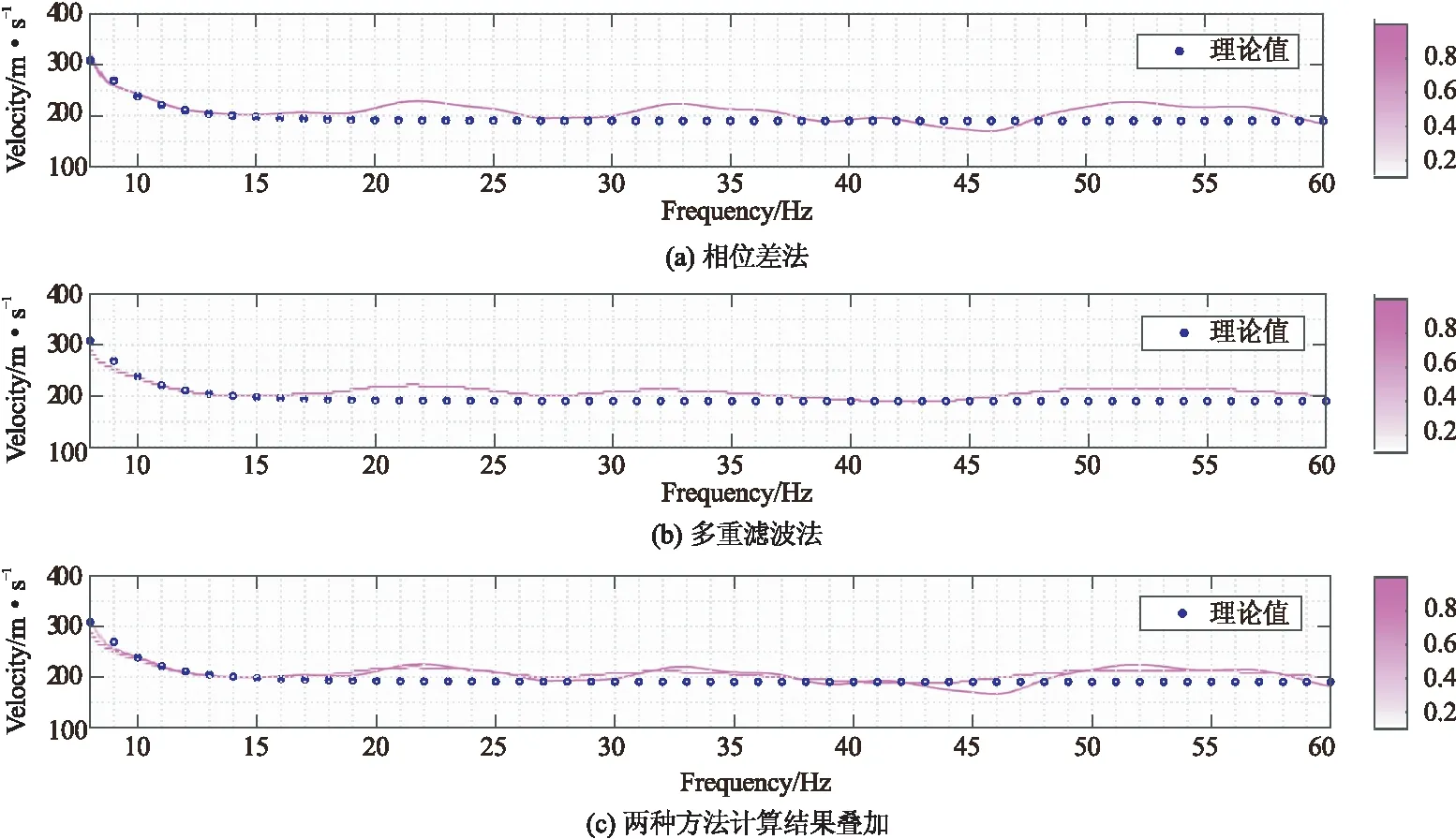
图2 两层模型模拟数据第44道和第46道不同方法计算频散曲线对比Fig.2 Comparison of the dispersion curves of the 44th and 46th channels of the two-layer model calculated by different methods

为避免反射波、直达波和折射波等干扰波以及瑞雷面波各模式间对计算结果的影响，因此在计算之前需要F-K进行模式分离。由于采集的数据为等间距线性排列，因此可以在频率-波数(F-K)域进行模式分离。图3(a)为将图1所示的地震记录转换到F-K的结果，从图中可看出不同模式的瑞雷波相互分离。在F-K域中将其他模式切除，仅保留基阶模态，如图3(b)所示。将F-K域中的基阶模态数据进行傅里叶反变换，便可得到如图4所示的时间-空间域基阶瑞雷波数据。

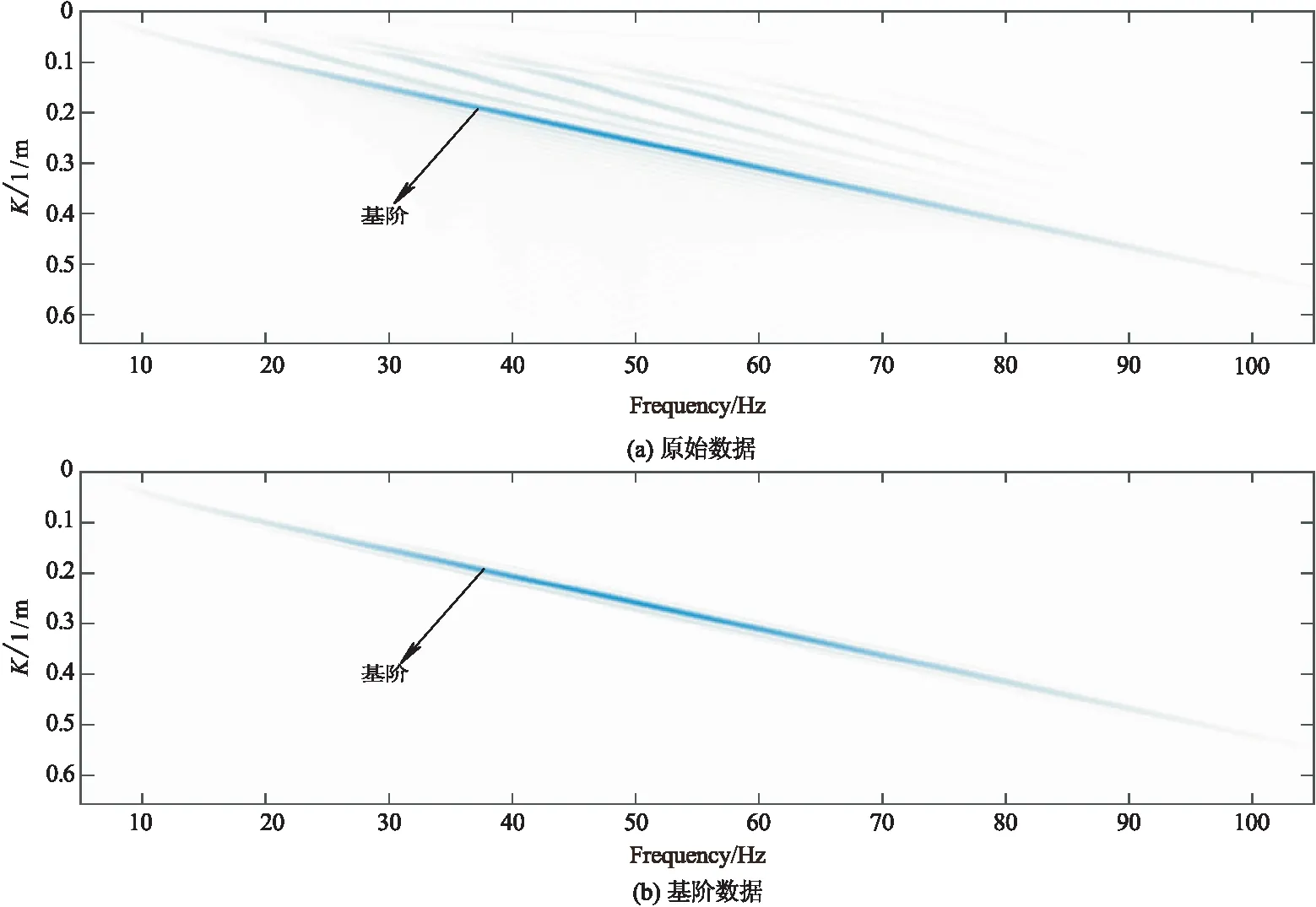
图3 两层介质模型频率波数谱Fig.3 Frequency wavenumber spectrum of two-layer model

图4 F-K模式分离后的两层模型基阶地震记录Fig.4 Fundamental model seismic records of two-layer model after F-K mode separation

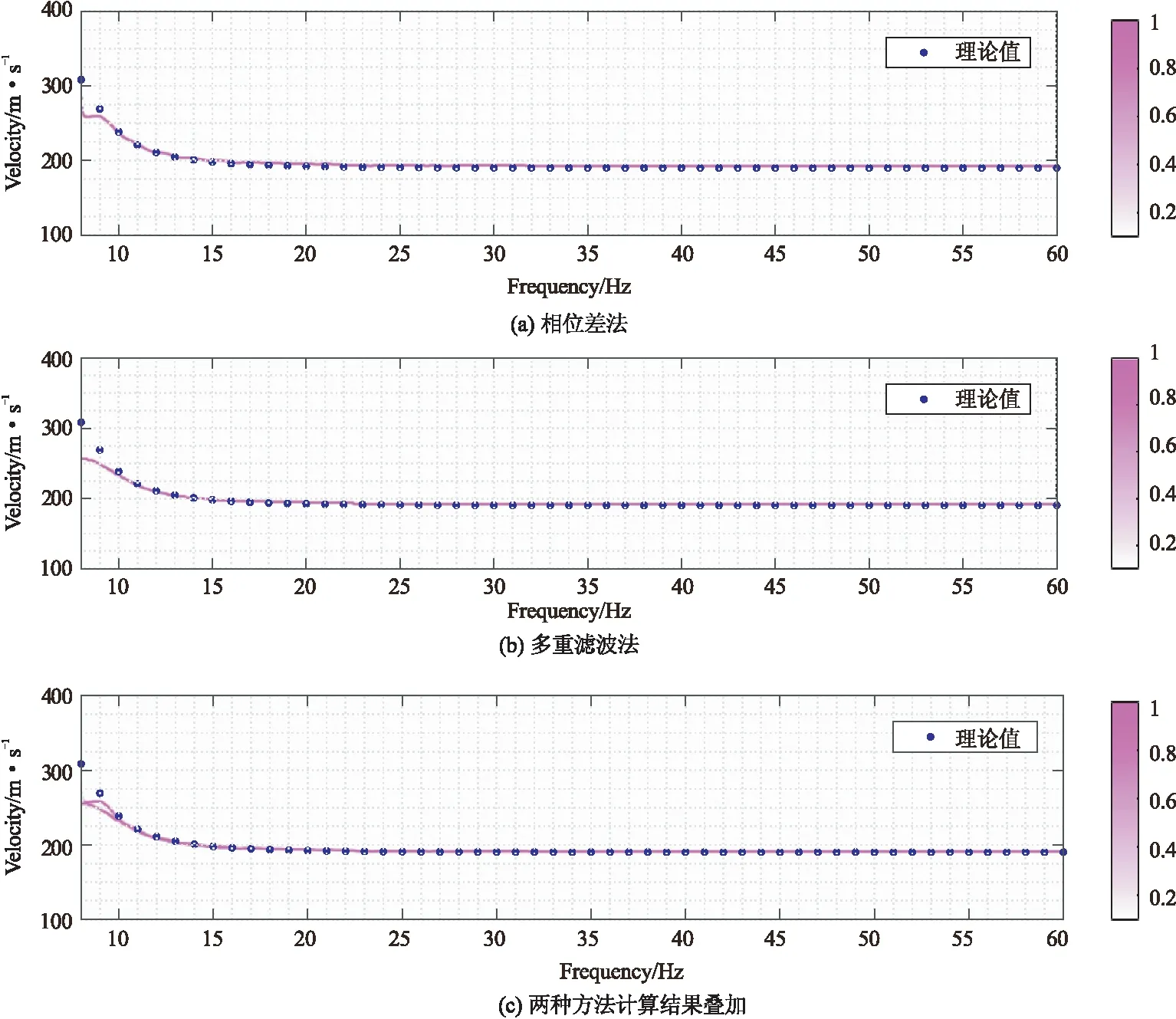
图5 不同方法计算两层模型F-K分离后的第44道和第46道的频散曲线对比Fig.5 Comparison of the dispersion curvesof channels 44 and 46 after the F-K separation of the two-layer model calculated by different methods

对于F-K模态分离后的基阶数据，选取第44道和第46道采用相位差法和多重滤波法计算频散谱，结果如图5所示，图5(a)～图5(c)分别依次代表相位差法、多重滤波法和两种方法计算结果叠加的频散谱与理论值的对比图。从图中可见，利用模式分离后的基阶地震波数据分别用两种方法计算得到的频散曲线与理论值吻合程度均较好。在8～20 Hz频率段，相位差法与理论值之间的误差最大值仅为3%，多重滤波法的误差最大值仅为2.4%，而两者叠加后的误差最大值仅为1.8%；频率在21～60 Hz时，三者的频散结果基本与理论值重合。通过将F-K分离后的数据采用两种方法计算的叠加谱与理论值对比可知，相对于单一方法，前者可以提供更多的信息。而通过提高面波频散曲线提取的准确度，也能说明将两种数据计算的频散信息叠加是可行的。

3.2 斜坡模型

为了进一步验证通过相位差法和多重滤波法相互结合计算频散曲线来提高瑞雷面波探测的横向分辨率的情况，特设计如图6所示的斜坡模型。模型大小为90 m×50 m，左端厚度5 m,右端厚度10 m。第一层纵波速度为VP=800 m/s，横波速度VS=200 m/s，密度ρ=2.0 g/cm3；第二层纵波速度VP=1 200 m/s，横波速度VS=400 m/s，密度ρ=2.0 g/cm3。数值模拟采用高精度交错网格有限差分法，震源为主频25 Hz的雷克子波，分别位于(4,0)、(9,0)、(14,0)、(76,0)、(81,0)和(86,0)处。检波器位于地表，从19 m到71 m处；道间距为1 m，共有53道。六个震源位置模拟得到的地震记录选取位于(4,0)处的地震记录如图7所示。

图6 斜坡模型和参数Fig.6 Slope model and parameters

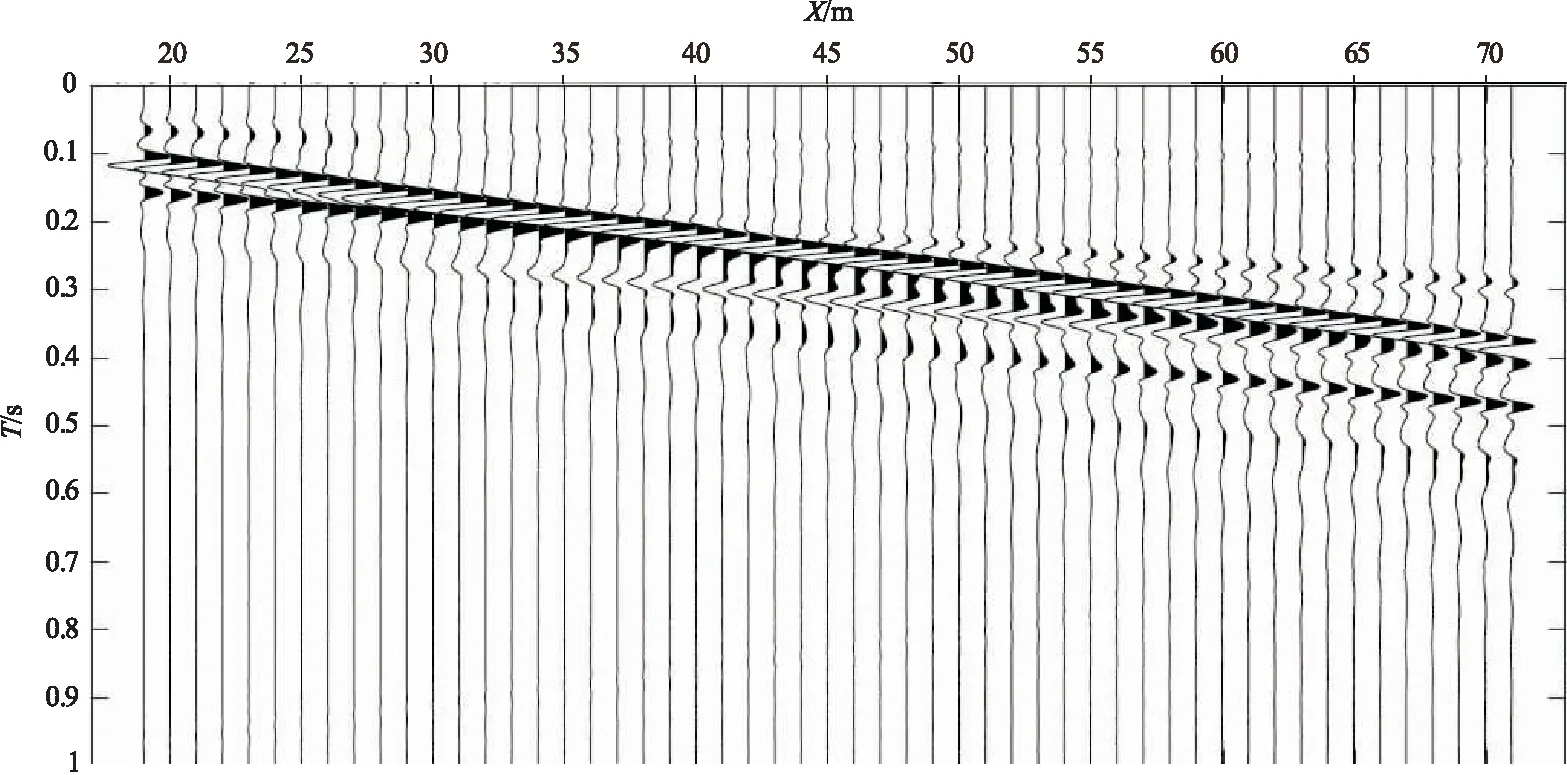
图7 斜坡模型原始地震记录(震源位于地表4 m处)Fig.7 Original seismic record of slope model(the seismic focus is located at 4 m on the ground)

对于上述六个不同震源位置获得的地震记录进行F-K模式分离得到基阶面波，然后利用多道面波分析方法(MASW)计算得到的频散曲线如图8所示，从图8中可见，尽管震源位置不同，但计算得到的频散曲线基本吻合，这也进一步说明了模拟结果的正确性。

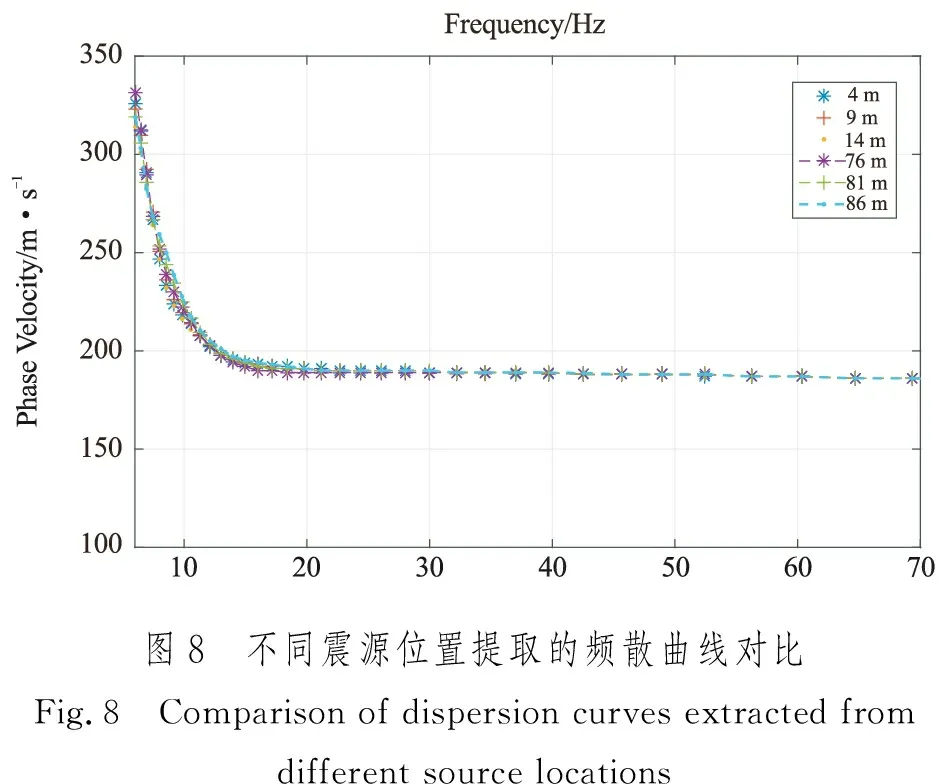
从另一方面来看，多道面波方法虽然提取的频散曲线的准确度较高，但横向分辨率较低。接下来采用相位差法和多重滤波法结合的方式，利用两道数据计算出频散曲线谱。为了使计算的频散谱更加稳定，在计算过程中采用三道数据两两计算后再平均，这样依次向后滑动每三道就可以提取到51条频散曲线。由于本文主要研究的是频散曲线的提取，因此没有对频散曲线进行反演，避免由于反演带来相关的误差而影响对结果的分析。最后将频散曲线按照半波长法进行转换得到如图9所示的相速度拟二维剖面图。为了进一步说明该方法的有效性，同样采用多道(滚动式)的方法对该模型数据进行处理，结果如图10所示。从图9和图10中均可以看出相速度在横向上的变化与倾斜界面的倾向是一致的，并能分辨出界面在横向上的变化。另外，从图10中还可以看出，采用多道滚动式处理的界面更加平滑，尤其在浅层内更为明显。但这种方法由于不断移动排列会大大延长工作时间，耗费更多的人力和物力。因此相对于采用常规MASW方法仅得一条频散曲线而言，利用相位差法和多重滤波法相结合计算两道的方式，不仅可以计算出高精度的频散曲线，而且只用一个排列便可以提取多条频散曲线，大大节省了人力和物力，具有良好的实用性。

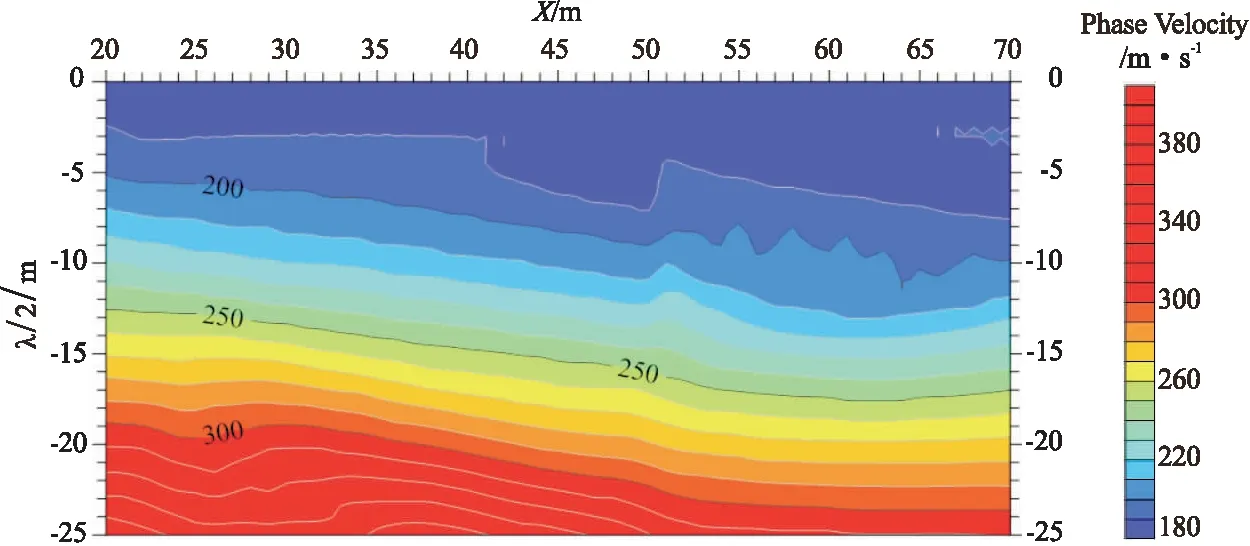
图9 叠加处理的斜坡模型面波速度剖面Fig.9 Surface wave velocity profile of slope model with superposition processing

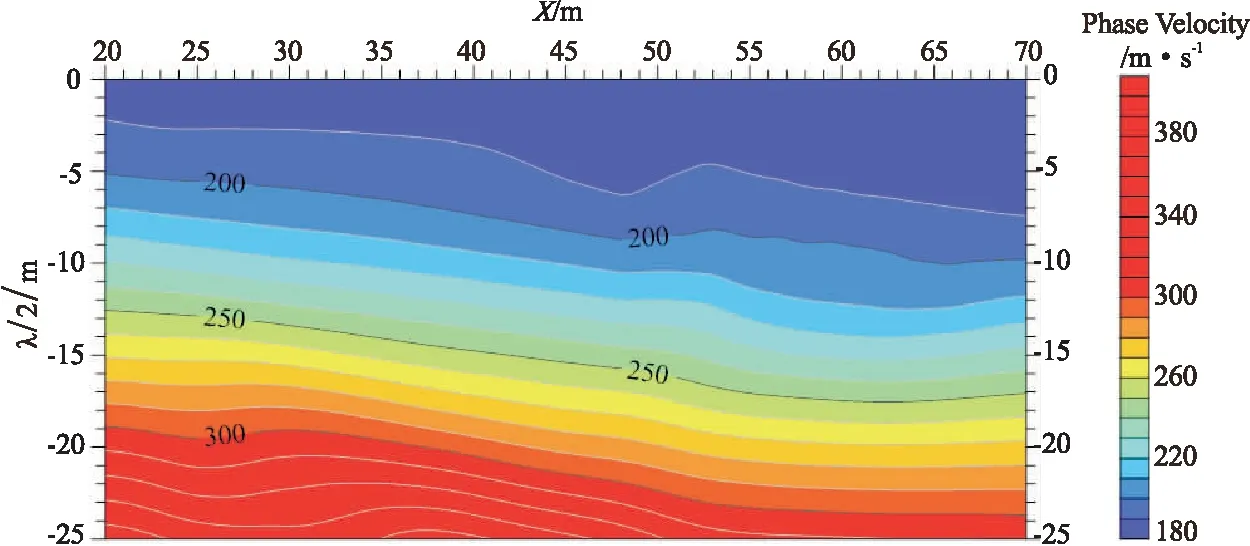
图10 多道滚动式分析方法斜坡模型面波速度剖面Fig.10 Surface wave velocity profile of slope modelunder multi-channel rolling analysis method

4 混凝土球模型测试

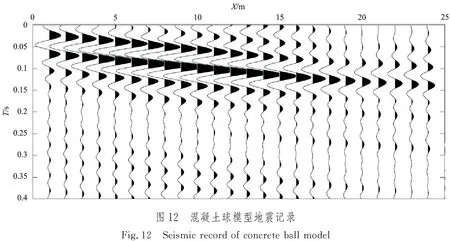
为测试本文所提出方法的实用性，对某实验场地埋设的混凝土球模型采集面波数据进行处理分析。该模型为直径1 m的混凝土球，埋深3.5 m，如图11所示。混凝土周围为密实的土层，面波数据采集现场布置的排列共有24道，道间距为0.5 m，混凝土球位于排列中间第12个检波器的下方。震源方式为锤击，分别在两端6 m和8 m偏移距处用18磅大锤激发，图12为在6 m偏移距下的实际地震记录，从图中可以看出面波能量较强。

对于采集得到的地震数据通过模式分离将干扰波去除，然后采用相位差法和多重滤波法计算其频散谱并进行叠加。为验证该方法在不同偏移距下也能够进行叠加处理，分别对同一排列两侧的6 m和8 m处的偏移距提取同一位置的频散曲线，并对其进行叠加，结果如图13所示。从图中可见，在同一位置处尽管偏移距不同，但是提取的频散曲线基本一致。相比于叠加处理结果，两处偏移距下的最大误差仅4.3 %，证明了叠加的可行性，并且发现进行叠加处理后的频散曲线更加稳定。

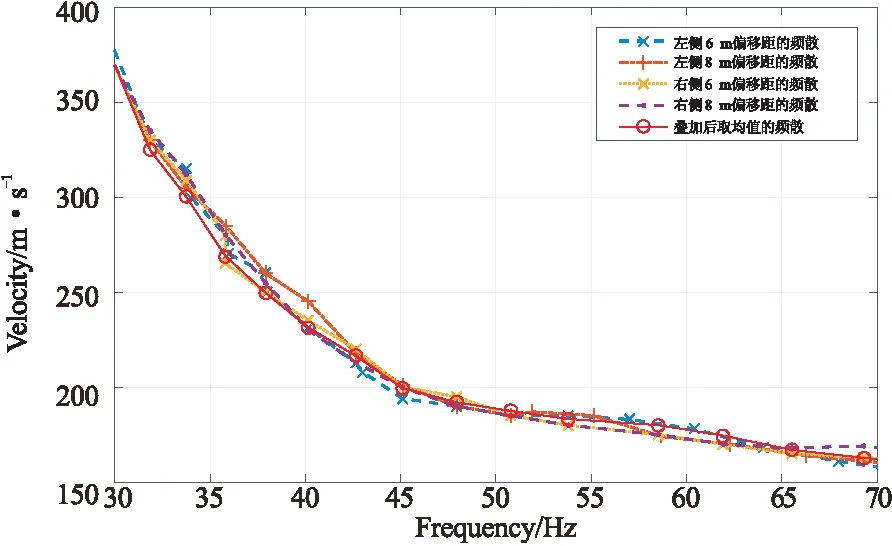
图13 不同偏移距的频散曲线Fig.13 Dispersion curves with different offset distances

图14为计算得到的该排列的23条频散曲线空间分布图，频散曲线间隔为0.5 m。对于计算得到的频散曲线同样利用半波长法转换得到如图15所示的拟二维相速度剖面，从图中可以清晰地看出在水平位置5.8 m、深度3.0 m处相速度值明显高于周围(图中用黑色虚线圈定位置)，这一异常与混凝土球在土层中表现为相对高速特征相吻合。异常在水平位置与埋设的混凝土球实际位置一致，仅在深度上略有差异，这主要是由于半波长法的近似性所导致。总之，该方法所提取的频散曲线较好，能够比较准确地反映地下地质异常体特征，在水平方向有较高的分辨率。另一方面，利用该方法进行探测，一条测线就可以得到一个二维断面，其探测效率大大提高。