计算机辅助设计凸轮轮廓线的方法研究

花 卉

信阳技师学院，河南 信阳 464000

凸轮从动件机构通常在绝大多数的机械系统中被采用，通过直接性表面接触将所需的运动传递给另一个机械元件。凸轮和从动件机构非常方便而且简单，它们之间很少有其他运动部件，所占据的空间非常小。一般来说，从运动学的观点来看，凸轮机构由3个不同的基本部分组成：驱动元件、从动件、从动件和固定框架。凸轮机构通常在大多数现代机械机构中被广泛应用，特别是在自动机械和仪器、内燃机和控制系统中应用最为广泛。虽然凸轮机构的自动化程度相对来说比较低，但由于其制造成本较低而且能够满足几乎任何从动件运动所需的一种最简单结构，因此应用范围较为广泛[1]。

1 凸轮机构设计概况

凸轮机构设计包括两个阶段：首先，选择满足规定运动学规范的适当传递函数；其次，机构几何优化，考虑构造约束。凸轮轮廓设计技术的发展通常基于样条曲线的使用。凸轮的运动特性通过标准运动函数、抛物线函数、简谐函数和摆线函数的组合来综合应用。在过去，凸轮轮廓的设计是一项烦琐的工作，需要应用图形或分析方法[2]；而在当今的大多数应用中，凸轮轮廓是由数控铣刀加工而产生的，数控铣刀可以依据数控编程来切削凸轮轮廓，可以在不需要首先明确凸轮轮廓的情况下生成所需要的从动件运动轨迹。凸轮机械设计的一个重要特征就是在不同半径的圆弧连接的切点处突然做加速度变化[3]。任何凸轮的轮廓取决于所需的从动件运动特性，通常以位移和速度属性来表达。在自动车床的情况下，形成平面凸轮形状的原始曲线（如螺旋形），通过车削具有所需尺寸和几何属性（如球形轮廓）的部件所运用的刀尖运动轨迹特性来控制。目前诸多文献中有各种各样的凸轮轮廓设计方法。

2 研究方法

文章通过凸轮轮廓线上3个连续点的矢量差的解析表达式，计算了从动件运动的凸轮廓线曲率。然后，采用类似的算法设计从动件的运动特性。根据凸轮轮廓上3个连续点的同一矢量模型的初等几何，通过迭代过程计算速度、加速度和冲击，呈现出了铣刀运动轨迹样条线实时位置的效果，将矢量差的解析表达式计算结果输出到数控编程运算程序中，开创了一种新的计算机算法。该方法适用于低速机械或低精度应用，或者机械设计尺寸减小到毫米（最小机构）甚至微米（微型机构）的情况。在这种情况下，多项式凸轮轮廓的制造变得困难，甚至更复杂也更难以验证。该研究实例证明了该方法的工程可行性，并与凸轮从动件机构的解析设计参数进行了对比。

3 凸轮从动件运动分析的数值方法

任何凸轮的轮廓取决于所需的从动件运动特性，通常以位移和速度属性表示。对于具有直线（平移）平面从动件的凸轮，如图1所示，凸轮围绕点OA旋转，平面从动件始终移动，因此其几何轴始终在OAB线上。Rb是基圆半径。凸轮上的基准线从一固定点开始转动到凸轮与从动件在A点接触时所运动的时长t时，基准线所运动的角度为θ。

图1 具有主动平面从动件和凸轮轮廓上3个连续点的凸轮

铣刀的半径为Rc，中心在Oc点。S（θ）是从动件的位移距离与旋转角度θ构成的一种函数关系。在铣刀运动过程中，凸轮轴在每个时间和每个角度上都可以按规定的角度旋转OA，铣刀的中心可以编程设置为这样一个位置，即从动件的位移将由功能S（θ）规定。因此，给定的数据是铣刀半径Rc，凸轮中心的位置旋转OA和每个角度所需的铣刀中心位置Oc（距离a等于半径R加Rc）。假设凸轮dθ围绕OA进行小的增量旋转，从动件的中心线逆时针旋转dθ。虚线表示从动轮的位置变化。向量R相对于中心线的位置是φ。

铣刀中心Oc的坐标计算如下：

点A的极坐标、凸轮和刀具的接触点如下：

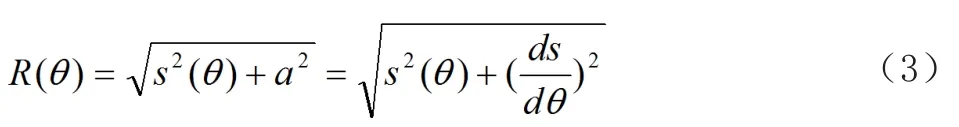
凸轮最小廓线曲率计算的解析式为

式中：Rb为基圆半径；s(θ)为从动件的位移。

s(θ) 和导数s＇(θ)、s＇＇(θ) 的计算是一个烦琐的过程，通常会导致很大的误差，这取决于相应的时间增量。速度、加速度和冲击的误差分别与1/Δt、1/Δt2和1/Δt3成正比。根据从动件位移确定铣刀和凸轮表面接触点近似图形，采用近似数值方法计算凸轮轮廓曲率ρ。然后根据凸轮廓线确定从动件的速度和加速度屈服，并用图形表示法帮助用户接受或拒绝凸轮-从动件运动副的特性。

由于曲率中心在凸轮表面上是静止的，凸轮轮廓曲率的大小和定义瞬时曲率中心的矢量不会因凸轮旋转的微小变化而改变[3]，凸轮轮廓上的3个连续点位于半径为ρ的圆的同一圆弧上，中心位于O（Xρ，Yρ），笛卡尔坐标为（Xi-l，Yi-l），（Xi，Yi），（Xi+l，Yi+1）。这些点属于等角 AO 的连续半径，每个弧的曲率根据毕达哥拉斯定理计算如下：

式中：xρ和yρ是弧中心的坐标。

式（5）屈服得到

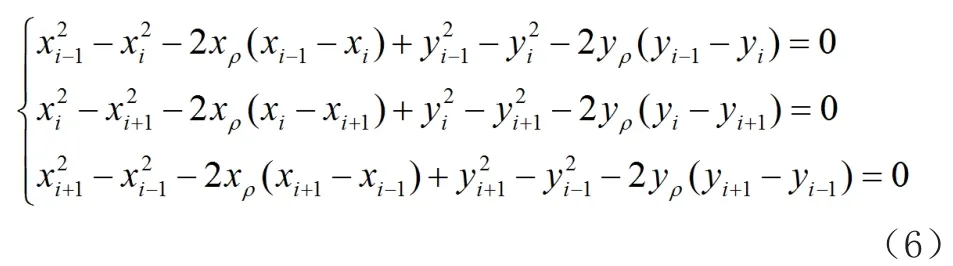
根据式（6）得出xρ和yρ的坐标。然后计算凸轮轮廓曲率ρ，公式如下：

式（7）根据凸轮-从动件配置和数据库[2]中可用的从动件位移的几何关系，得出从动件运动位移s（θ）的凸轮轮廓曲率。对于凸轮轮廓上的3个连续点，角度Δθ等于360/N，其中N是构成凸轮轮廓的离散点的数目。对于大量的点N，Δθ变得非常小，然后考虑到时间的无穷小增量，凸轮轮廓的速度、加速度和冲击度分别计算如下：

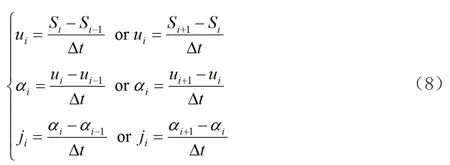
为了获得更高的精度，式（8）将被视为

式（7）～式（9）确定了从动件位移、速度、加速度和冲击以及凸轮轮廓曲率。利用上述公式，开发了凸轮从动件设计程序，用于计算凸轮从动件的设计参数。该算法综合了凸轮-从动件运动副的各种构型和任意凸轮转角下从动件位移的几何关系。必须首先限制时间步长增量，通常是360度的倍数。然后，用户从可用功能中选择从动件运动特性，或提供特定从动件运动所需的数据。式（3）的解和所选时间步长对应离散点的限制需要此方程[3]。算法是将这些点的坐标存储在一个特定的数组中。为了确定凸轮轮廓和速度、加速度和支撑配置，可通过式（7）和式（9）的解得出。由于该算法适用于低速运动副或低精度应用场合，与解析相比，1440点的离散化结果具有较高的精度。当然，离散化取决于所研究的特定凸轮-从动件副，并且该方法提供了压力角和曲率半径大小的适当检查。以上从动件盘形凸轮机构为例说明了该方法的应用。首先，从合并的数据库中选择凸轮从动件结构和相应的从动件位移关系。从式（8）中获得凸轮从动件位移、速度和加速度图。然后，通常采用位移和速度的特点来表示从动件运动的特性。凸轮从动件运动特性绘制在通过摆线式从动件运动的分析方法计算的相应点上[4]。

4 结论

文章提出的算法是通过对凸轮轮廓上的3个连续点采用矢量差分算法来描述期望从动件运动的凸轮轮廓曲率的数值过程。通过一个类似的迭代过程，定义了从动件的运动特性（速度加速度、冲击），并验证了凸轮廓线设计的可接受性。数值算例验证了分析设计方法的正确性，使计算误差最小化，并证明了其工程可行性。