基于VMD分解的MFCC+GFCC无人机噪音混合特征提取方法

邹瑛珂，李祖明，刘晓宏，贾云飞

（1.南京理工大学机械工程学院，江苏 南京 210094; 2.南京工程学院电力学院，江苏 南京 211167;3.盐城供电公司，江苏 盐城 224000）

0 引 言

近年来，由于传感器、芯片和控制理论的快速发展，大量的廉价小型四旋翼无人机被应用在农保、安防、摄影、娱乐、军事等领域。与此同时，四旋翼无人机所产生的各种社会问题（如偷拍、妨碍飞行器飞行、伤害路人等事件）频发。而在国防领域，利用无人机进行军事情报窃取或直接利用无人机进行恐怖袭击的可能性越来越高。因此如何在各种环境下对无人机进行探测预警成为了一个新的课题。由于无人机体积小、速度低、飞行高度较低，很难被常规电磁波雷达探测。若使用光学雷达，有被障碍遮挡的问题存在，且在复杂环境背景或无人机自身有隐蔽涂装的情况下识别率很低[1]。但四旋翼无人机的声音信号较大，且不易被改变，因此成为了比较有效的新颖探测方案。针对无人机声探测领域的研究开始于2010年，目前取得了一定成果。在国内，张一闻等[2]提出了利用FFT、EMD+MFCC等特征结合诸如SVM、VQ等机器学习算法分类器以实现对无人机的识别，丘恺彬等[3]也提出利用MFCC+EMD能量占比实现不同型号无人机的区分。在国外，Jeon等[4]也尝试使用深度学习算法研究UAV声音检测，最后发现循环神经网络效果最好，为将深度学习算法应用到该领域提供了先例。这些算法在高信噪比条件下识别率较高，但由于这些算法本身存在鲁棒性较低的固有缺陷，在面对诸如嘈杂街道等环境下识别率会有明显下降，或者需要较多的样本数量，然而目前网络上并没有相关公共数据集。本文主要针对无人机声信号在含噪环境中的特征提取进行深入研究，探求在该环境下比较好的特征提取方法，以解决无人机声信号在高/低信噪比情况下的识别问题。

1 无人机声学特性分析

通过采集四旋翼无人机在飞行时的飞行噪音信号进行分析。时域下无人机噪音信号如图1所示。与其他声学信号一样，时域信号幅值随着无人机与声传感器的相对距离而发生变化，距离越大强度越小。

图1 时域下无人机噪声信号

通过傅里叶变换可得其频域特征，如图2所示。可以看出其能量主要集中在200～2 000 Hz、7 600～9 900 Hz的范围之间，符合人耳20～20 kHz听觉范围。

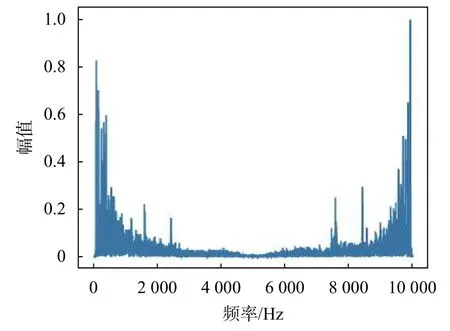
图2 无人机噪声频谱图

通过相关文献得知，无人机所产生的噪音主要来自3个方面：1）电机转动所产生的机械噪音；2）旋翼与空气发生高速相对运动所产生的气动噪音；3）机体与空气摩擦所产生的噪音。

但第一个和第三个方面相对气动噪音频率高幅度低，在远场环境下捕捉困难，信噪比过低。因此应针对气动噪音进行捕捉。由于风的影响和机体自身运动所产生的多普勒效应，使用传统的MFCC与FFT进行信号分析效果并不佳，不太适合运用于工程当中。因此需要采用其他特征提取算法能够解决风噪的问题。

2 特征提取

2.1 变分模态分解

针对该类非线性、非平稳信号，传统方法一般使用经验模态分解方法（empirical mode decomposition，EMD），但此方法由于理论自身缺陷存在波形混叠、端点效应等负面现象，严重影响对信号的分解。K·Dragomiretskiy等[5]提出了一种全新的自适应分解方法——变分模态分解（variational mode decomposition，VMD），该方法不但可以极大程度缓解EMD的固有缺陷，且对噪音的鲁棒性好，分解出的IMF分量数量固定，可以准确分解出不同频率段的信号。其核心是通过迭代搜索约束变分模型的最优解来自动获取固有模态函数的带宽以及核心频率，从而按照频率对信号进行分解。利用其约束变分模型引入二次乘法因子来降低干扰，同时使用拉格朗日乘子法将其转化为非约束变分问题。最后得到增广拉格朗日表达式[5]为：

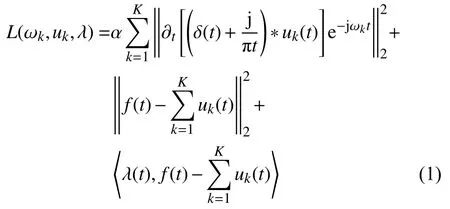
式中：f——原始信号；

uk——所得模态函数；

ωk——各个模态中心频率；

α——惩罚因子；

λ——拉格朗日因子。

最后利用ADMM算法迭代更新ωk,uk,λ，从而求得该模型的解。为求解方便将uk转化至频域，最后可得三者的更新公式[6]为：

2.2 VMD-IMF能量占比

跟EMD分解理论一样，一个信号可以由多个VMD分解所得的IMF叠加而成，可以根据重构算法反向重构至原信号。而该种分解得到的每个IMF是由信号中拥有相同中心频率的特定频率信号组合。在K=8的情况下无人机噪音、安静公园与嘈杂街道每个IMF信号能量与原信号的能量占比经过归一化后如图3～图5所示。

图3 无人机噪声信号IMF能量占比

图4 安静公园噪声信号IMF能量占比

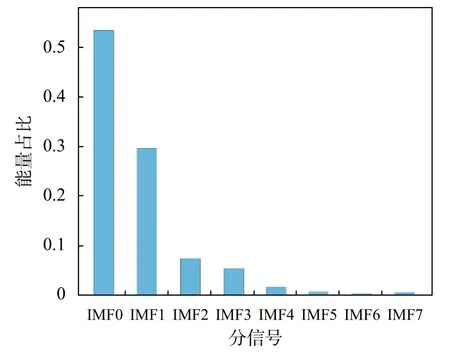
图5 嘈杂街道噪声信号IMF能量占比

可以看出二者有较大差别。说明每个分量的能量与原信号的能量占比可以作为识别无人机噪音的特征量之一。且还可利用所分解出的IMF信号进行进一步处理获取更多特征维度。

2.3 MFCC特征提取

人类听到声音的原理为机械震动在耳蜗的入口产生驻波，引起基底膜以与输入声波频率相称的频率协调在此频率上的最大幅度震动。其中基底膜的工作特点为：1）不同地方的细胞膜频率响应不同；2）基底膜被视为非均匀滤波器组；3）滤波器组中的单个滤波器中心频率和滤波器带宽的比值可视为常数。

因此在语音信号处理方面广泛采用按照人耳对不同声音频率敏感程度所设计的MEL滤波器组对语音信号进行滤波，获得其在不同频率范围内的能量分布。其响应函数为[7]：

其中f（m）为第m个滤波器中心频率。

通过MEL滤波器组后进行一系列变换后可得MFCC。其提取过程如下所示：1）信号预处理（包括分帧、预加重、加窗）；2）对信号进行VMD分解得到IMF信号；3）将2）中所得信号作FFT求取能量谱，并将其通过MEL滤波器组；4）取对数进行离散余弦变换。

无人机噪声信号VMD分解后IMF0信号某帧MFCC图像如图6所示。其中颜色越偏红，说明该m阶MFCC值越大，表示信号频谱的能量在第m个滤波器对应频率范围的能量分布大。相反，颜色越偏蓝，说明该m阶MFCC值越小，表示信号频谱的能量在第m个滤波器对应频率范围的能量分布小。

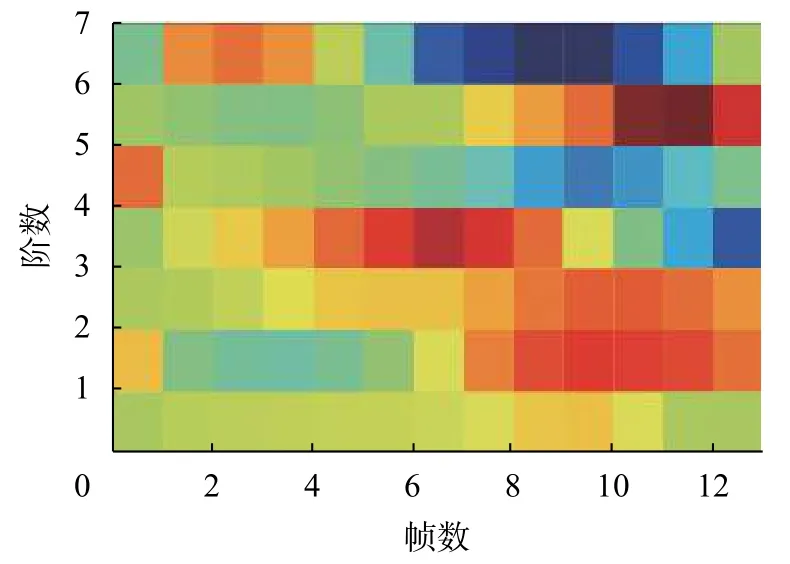
图6 无人机噪声信号IMF0某帧MFCC图

嘈杂街道、安静公园噪声信号VMD分解后IMF0信号某帧MFCC如图7～图8所示。

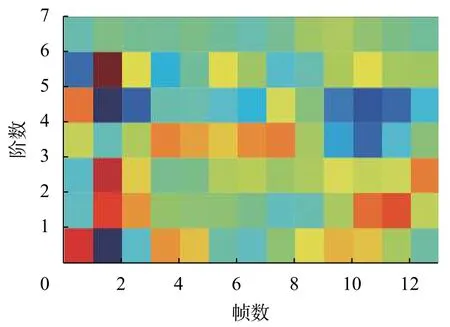
图7 嘈杂街道噪声信号IMF0某帧MFCC图

图8 安静公园噪声信号IMF0某帧MFCC图

为了体现连续信号每一帧的关联性，得到目标噪声的MFCC后，通过差分计算得到其一阶差分参数ΔMFCC，与之前的MFCCCt（n）一起作为特征量。ΔMFCC通过如下式求出：

由于之前对信号进行了VMD分解，因此本算法对VMD分解所得IMF信号进行变换得到更多的MFCC特征量。

2.4 GFCC特征提取

与MEL滤波器类似，GammaTone滤波器是一组用来模拟耳蜗频率分解特点的滤波器模型。但前者并没有考虑到耳蜗基底膜的主动反馈性和对频率变化响应的非线性，因此使用GammaTone滤波器组引入了非线性变化，鲁棒性更好、抗噪能力更强，可以用于音频信号的分解，便于后续进行特征提取。由于使用该滤波器时中心频率f0相对于衰减因子b足够大，因此可以简化滤波器频域响应表达式。组成其滤波器组的滤波器频域响应表达式[8]为

其中n为滤波器阶数。

经过研究取n=4，其中衰减因子b与中心频率关系为：

经过GammaTone滤波器后所提取的特征参数称为GFCC。无人机噪声信号VMD分解后IMF0信号某帧GFCC图像如图9所示。其中颜色越偏红，说明该m阶GFCC值越大，表示信号频谱的能量在第m个滤波器对应频率范围的能量分布大。相反，颜色越偏蓝，说明该m阶GFCC值越小，表示信号频谱的能量在第m个滤波器对应频率范围的能量分布小。

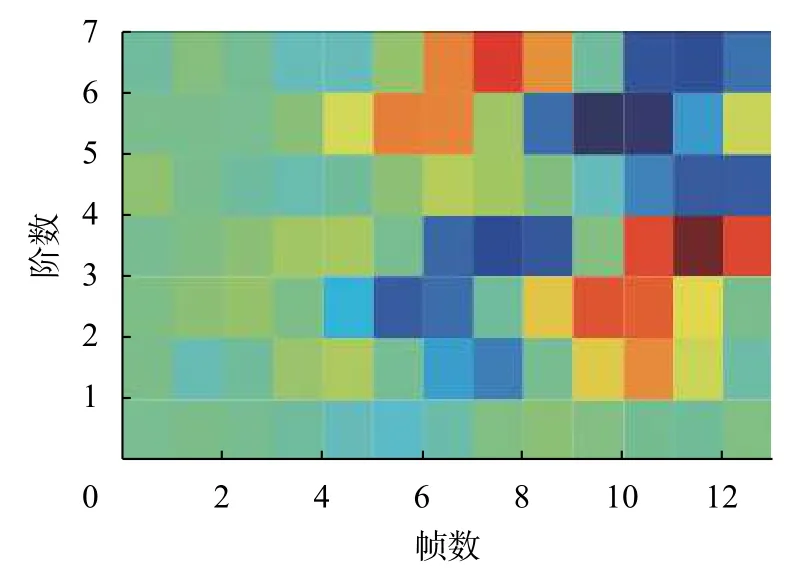
图9 无人机噪声信号IMF0某帧GFCC图

嘈杂街道、安静公园噪声信号VMD分解后IMF0信号某帧GFCC如图10～图11所示。

图10 嘈杂街道噪声信号IMF0某帧GFCC图

图11 安静公园噪声信号IMF0某帧GFCC图

该滤波器组相比于MEL滤波器组为非线性滤波，因此GFCC拥有更高的鲁棒性。与MFCC类似，其提取过程如下所示：1）信号预处理（包括分帧、预加重、加窗）；2）对信号进行VMD分解得到IMF信号；3）将2）中所得信号作FFT求取能量谱，并将其通过GammaTone滤波器组；4）取对数进行离散余弦变换。

同样，为了体现连续信号每一帧的关联性，得到目标噪声的GFCC后，通过差分计算得到其一阶差分参数，与之前的GFCC一起作为特征量。由于之前对信号进行了VMD分解，因此本算法对VMD分解所得IMF信号进行变换得到更多的GFCC特征量。

3 随机森林算法

随机森林算法是机器学习、计算机视觉等领域内应用较为广泛的一个分类器，也可以作为一种数据降维的手段[9]。近年来也被广泛应用到了基于各种特征的语音信号识别领域[10]。通过集成学习的思想，将原本作为弱分类器的多棵决策树最后集成到一起，从而形成一个强分类器，以实现比较复杂的分类。

随机森林运用Bagging的思想，在变量（列）和数据（行）的使用上进行随机化，对训练集进行有放回地随机抽样生成很多分类树，每个树都是一个独立的判断分支，互相之间彼此独立。随机森林的优点在运算量没有显著提高的前提下提高了预测精度，解决了决策树面对高维特征的对象容易过拟合的缺点，对缺失数据有良好的鲁棒性，可以很好地对拥有多个特征的信息进行分类。其中生成决策树的算法本文中采用基尼指数[11]：

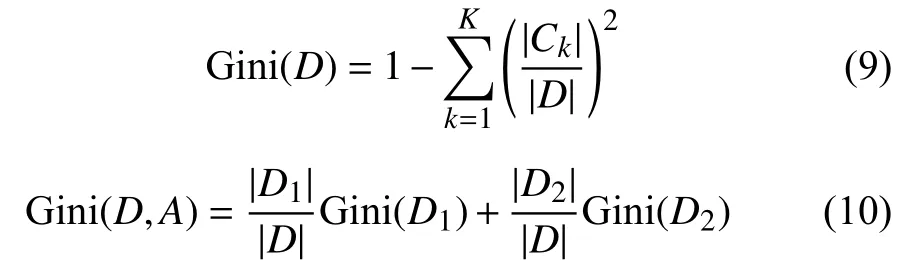
式中：D——整个训练集集合；

Ck——训练集中每种样本的数目；

D1与D2——每个按特征分类的两种类别集合。

基尼指数越小，集合不确定性越小，因此每棵决策树每个节点都选取基尼指数最小的特征分类点进行分类。

当在基于某此属性对一个新的对象进行分类判别时，随机森林中的每一棵树都会给出自己的分类选择，并由此进行加权输出。在本算法中相比其他机器算法，该算法不用进行相关参数的调整，且自带有降维和特征选择的功能，比较适合作为解决该类问题的分类器。

4 算法流程

结合上文所述特征和分类器，总结出本文提出的一种无人机噪音信号识别的算法流程如图12所示。

图12 算法流程图

该算法中，特征值MFCC与GFCC都是从由VMD分解所得的IMF信号中提取的，因此以下称为VMFCC与VGFCC。

5 仿真实验

仿真实验基于Python3.8，样本语音为利用NI数采和BM-K-5拾音器采集的的嘈杂街道环境音以及该环境下不同距离四旋翼无人机飞行噪音（10～20 m）、安静公园环境噪音以及该环境下的四旋翼无人机飞行噪音（10～20 m）。每种音频样本数为300，归一化后50%样本用于训练，采样频率为20 kHz，预加重系数为0.97，加窗类型为Hamming，帧长100 ms，帧移50 ms。VMD的K取8，GFCC/MFCC的倒谱系数数目取13，分别采用EMD能量占比+（Δ）EMFCC、EMD能量占比+（Δ）EGFCC、VMD能量占比+（Δ）VMFCC、VMD能量占比+（Δ）VGFCC、VMD能量占比+（Δ）VGFCC+（Δ）VMFCC特征，投入随机森林分类器中进行分类，所得结果如表1所示。

表1 本文特征与其他特征比较

从表中可以看出：

1）在使用VMD分解的特征提取算法中，其准确率比EMD分解后获取的同类特征提取算法最多高出11%。

2）其中在使用VMD能量占比特征的前提下使用（Δ）VGFCC在面对高信噪比样本时识别率低于（Δ）VMFCC，但在面对嘈杂环境下的无人机样本时识别率高于VMFCC。

3）VMD能量占比+（Δ）VGFCC+（Δ）VMFCC的识别率在面对不同距离高低信噪比的无人机噪音信号都高于二者单独使用时的识别率。

6 结束语

针对传统无人机声噪信号识别鲁棒性不高的问题，本文在前人提出的无人机声音特征提取方法上进行改进，将VMD能量占比和VMD所分解得到的GFCC作为在低信噪比环境下的识别特征，把可以自动挑选特征量的随机森林算法作为分类器进行试验，证明该混合特征对改善低信噪比下无人机声音识别正确率的有效性。但若距离较远（大于20 m）的情况下，信噪比进一步降低，其识别准确率有显著下降。因此下一步工作是寻找更好的分类器和特征提取算法，提高识别距离。