基于碳纤维复合材料的机器人臂杆优化设计*

□ 陆汉林 □ 胡利永 □ 孙宝寿 □ 詹建明 □ 王佳锋

1.宁波大学 机械工程与力学学院 浙江宁波 315211 2.浙大宁波理工学院 机电与能源工程学院 浙江宁波 315100

1 设计背景

随着机器人技术的不断发展,机器人在日常生活中的应用变得更加广泛,人们对机器人性能也有了更高的要求[1]。机械臂是机器人的主要组成部分,如何在满足机器人性能要求的同时减小机器人质量,提高机器人的负载自重比,是机器人轻量化研究的重要内容[2]。在传统设计过程中,机器人结构大多采用铸铁、铝合金等材料,虽然能够满足结构的基本强度和刚度要求,但是也存在负载自重比低、能耗高等问题。碳纤维复合材料具有强度高、质量小、可设计性强等优点,越来越多地被应用于结构的轻量化设计中[2-3]。

隋显航等[4]采用变壁厚碳纤维复合材料机械臂轻量化设计方案,在满足强度及刚度的要求下,使质量显著减小。陈丰[5]通过有限元分析方法,对碳纤维复合材料机械臂铺层方式进行研究,得到最优铺层数量和铺层顺序,满足设计要求。田龙飞[6]以铸铁工业机器人上臂刚度为指标,对碳纤维复合材料上臂铺层进行优化设计,并通过仿真分析验证其动态性能。杨峰[7]对由碳纤维复合材料和铝合金构成的混合结构机械臂进行优化分析,在满足设计要求的情况下,获得了更小的质量。Honarpardaz等[8]对厚度、质量变化的复合材料管和铝制管进行模拟测试,对比刚度指标。Caprino等[9]设计了一款应用于工业测量机器人的碳纤维复合材料机械臂,以固有频率为优化目标,采用能量优化方法进行优化设计。杨绍勇等[10]将NSGA-Ⅱ应用于碳纤维复合材料悬架控制臂结构,使刚度和一阶固有频率得到提高。

将碳纤维复合材料应用于机械臂的设计取得了一些成果,但现有研究并没有进行详细优化设计,仍然存在强度、刚度冗余。笔者采用等代设计法,在原有铝合金材料机器人臂杆的性能指标基础上,应用碳纤维复合材料对机器人臂杆进行优化设计,并以机器人臂杆刚度为指标,从铺层厚度设计、铺层角度优化、工艺可行性等方面进行研究,优化后碳纤维复合材料机器人臂杆不仅满足设计要求,而且轻量化效果明显。

2 三维与有限元建模

设计所参照的铝合金机器人臂杆如图1所示,其三维模型如图2所示。笔者主要以臂杆六为例进行机器人臂杆的轻量化设计。

▲图1 铝合金机器人臂杆

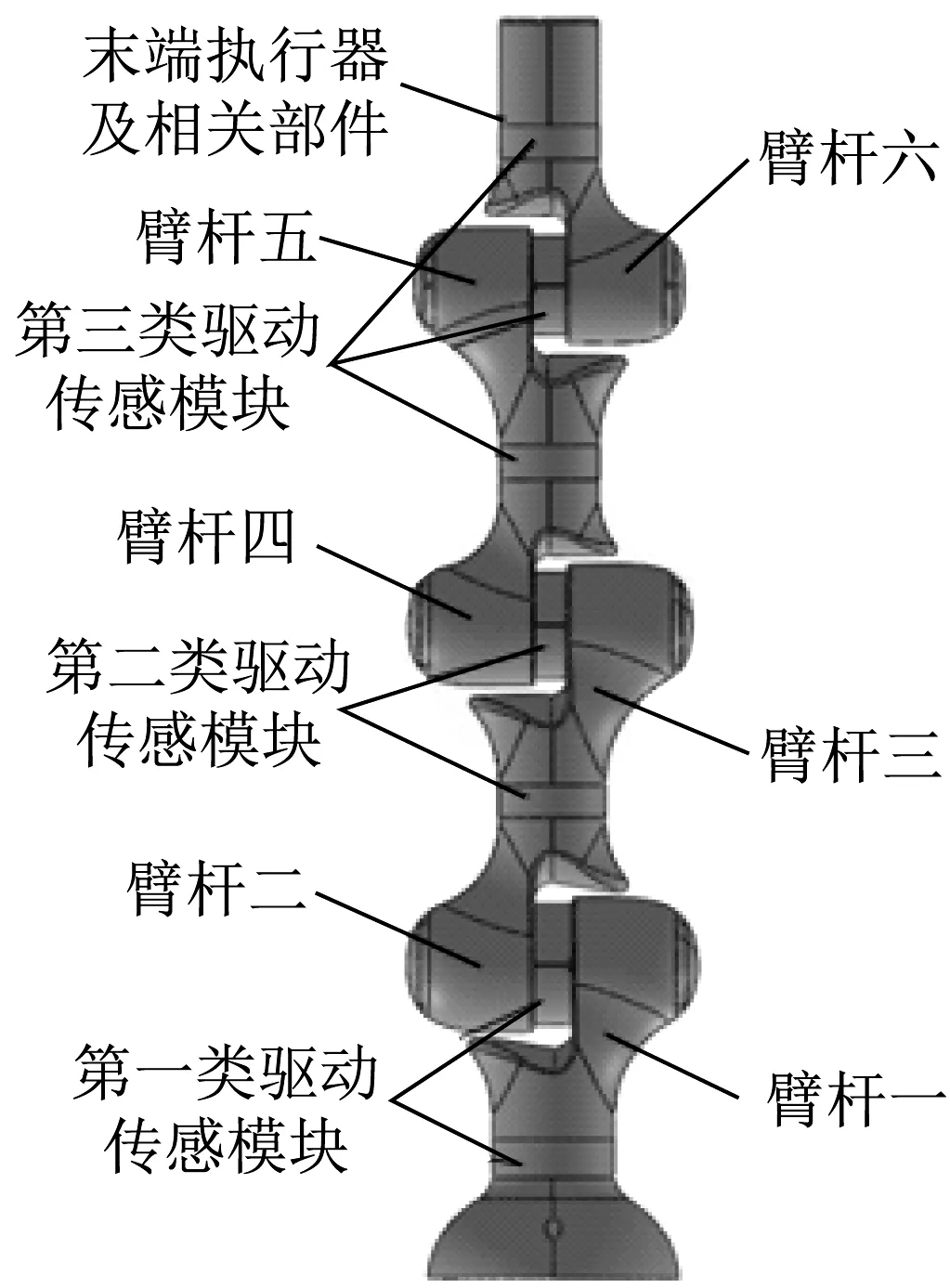
▲图2 机器人臂杆三维模型

简化上述机器人臂杆的三维模型,并在ABAQUS软件中构建机器人臂杆的有限元模型。三维网格采用C3D8R单元,网格划分后网格数量为235 346。机器人臂杆有限元模型如图3所示,大端直径为119 mm,小端直径为106 mm,所用T300/5208碳纤维预浸料的性能参数见表1。

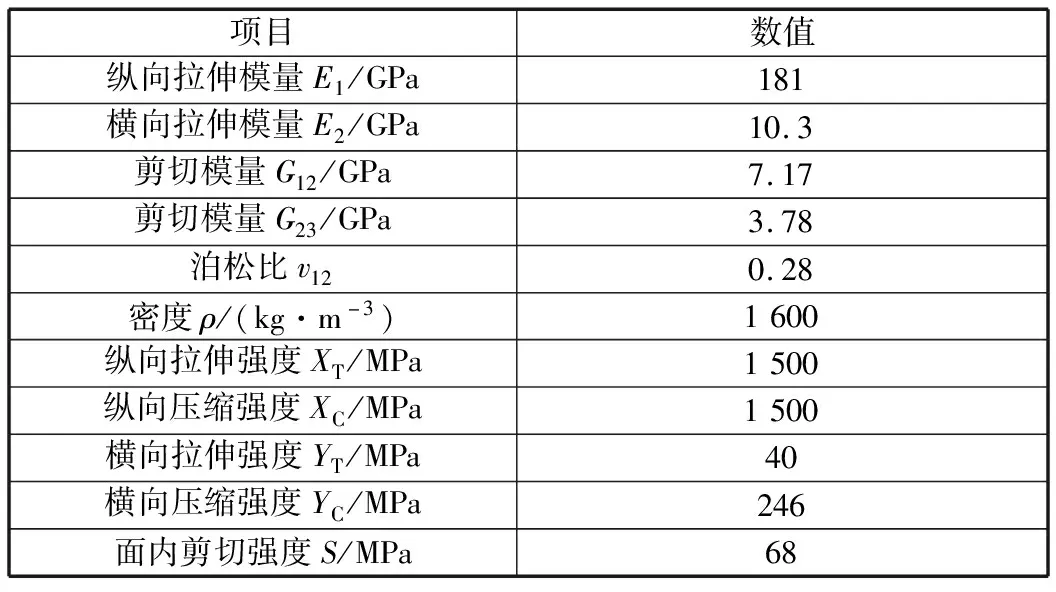
表1 T300/5208碳纤维预浸料+性能参数

3 设计工况

在不同的工况下,机器人臂杆的强度和刚度不同。为了保证机器人能够在各种情况下正常使用,一般需要考虑机器人的完全展开垂直、完全展开水平、部分展开倾斜等角度极限情况。笔者选择机器人臂杆实际工作过程中的五种工况进行有限元分析,各工况如图4所示。

▲图3 机器人臂杆有限元模型

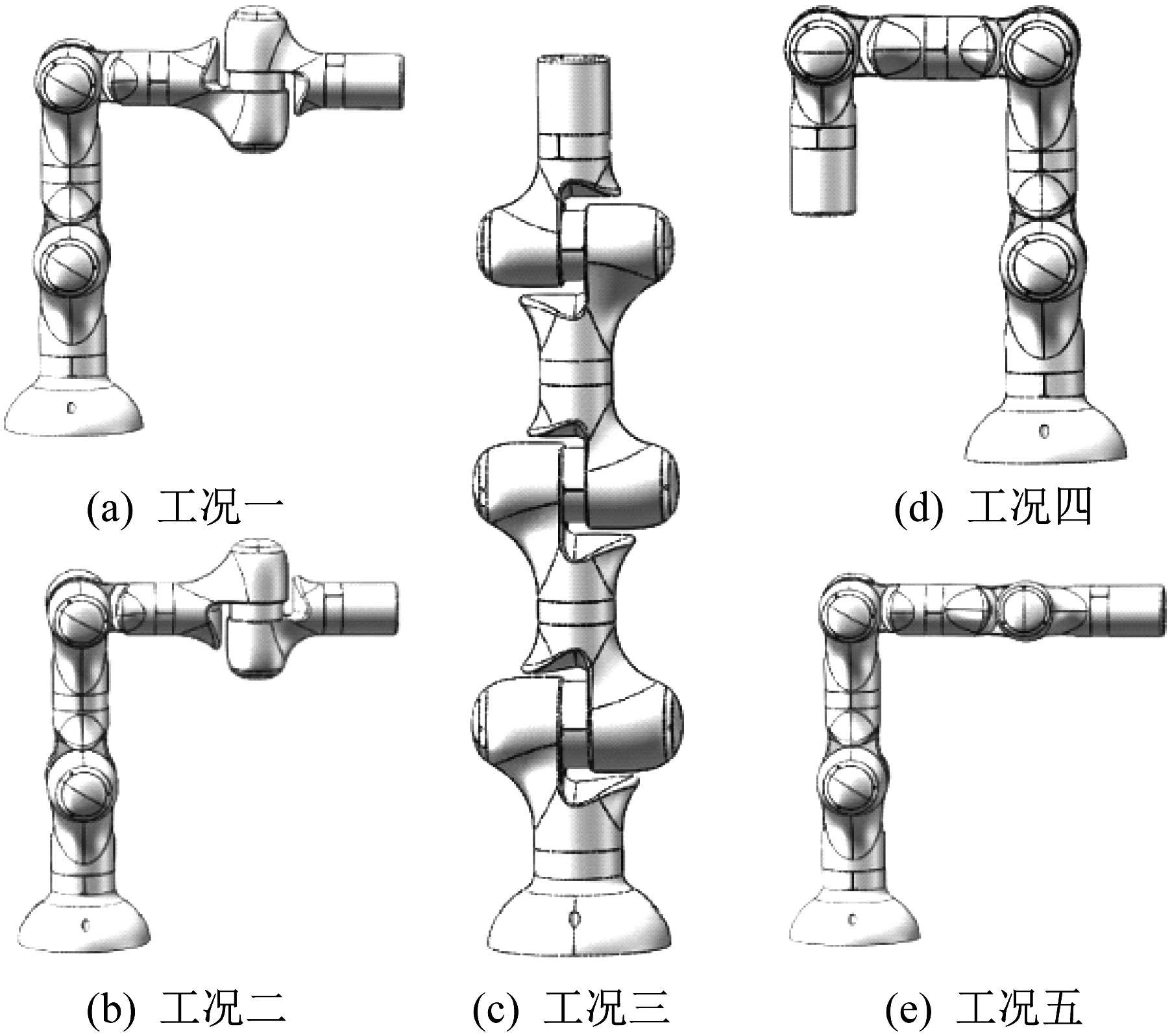
▲图4 机器人臂杆工况

臂杆六在实际工作中主要受到上端负载的集中载荷、螺栓力,以及自重作用。

4 铺层厚度设计

对碳纤维复合材料机器人臂杆进行铺层厚度设计,需要确定机器人臂杆的总体厚度及每一层碳纤维复合材料铺层的厚度。为保证内部布线和控制装置的使用空间,碳纤维复合材料机器人臂杆的总体厚度应该接近于铝合金机器人臂杆,即机器人臂杆总体厚度保持在3.5 mm左右。碳纤维复合材料单层铺层厚度为0.18 mm,铺层层数选择17～25层之间。根据上下对称的铺层要求,铺层层数应尽量选择偶数,以实现中面对称。由于碳纤维复合材料是各向异性材料,因此采用准各向同性铺层方式[11]和等代设计法,以原铝合金材料机器人臂杆的刚度为指标,测试各铺层厚度方案,最终确定铺层层数。

通过仿真分析,当碳纤维复合材料机器人臂杆铺层层数为22层时,碳纤维复合材料机器人臂杆在各工况下的最大变形位移基本都在铝合金机器人臂杆的最大变形位移范围内,满足刚度设计要求。碳纤维复合材料机器人臂杆与铝合金机器人臂杆的性能指标对比见表2。由表2可以看出,碳纤维复合材料机器人臂杆在工况二与工况五的情况下,刚度比铝合金机器人臂杆略差,其余工况下的刚度均满足要求。与铝合金机器人臂杆质量相比,碳纤维复合材料机器人臂杆减小39.6%,轻量化效果明显。

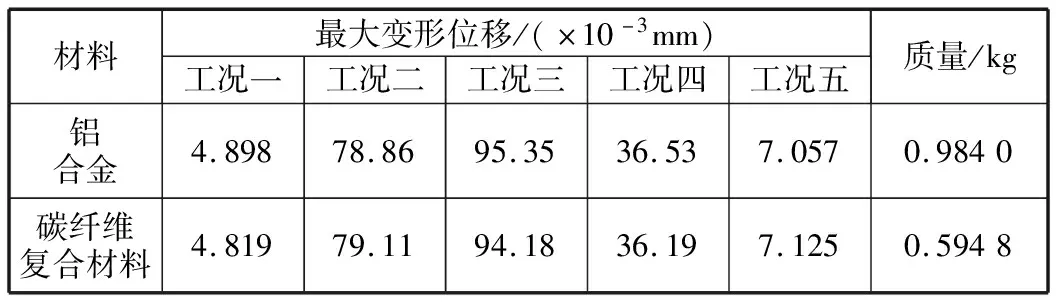
表2 机器人臂杆性能指标对比

5 试验分析

由于机器人臂杆的性能参数与碳纤维复合材料铺层之间不存在明显的函数关系,因此直接使用有限元软件对机器人臂杆进行铺层优化需要花费较长的时间,并且效率低下。笔者首先采用优化拉丁方试验方法进行试验设计,提取样本数据,然后采用近似建模方法建立函数关系,最后再进行优化。

碳纤维复合材料机器人臂杆铺层层数确定为22层,采用对称铺层方式。为了减少设计变量的数量,对11层铺层进行拆分处理。从上往下依次选择六个单层的铺层角度作为设计变量,设为θ1、θ2、θ3、θ4、θ5、θ6。最上面五个铺层与最下面五个铺层以θ6单层对称,即总体铺层顺序从上往下为θ1、θ2、θ3、θ4、θ5、θ6、θ5、θ4、θ3、θ2、θ1。

最上面11个铺层与最下面11个铺层根据均衡对称的原则进行对称设计,共有六个设计变量,如图5所示。

▲图5 铺层角度设计变量

碳纤维复合材料铺层角度通常从0°、45°、90°、-45°这四种角度中进行选择。如果按全因子试验设计,那么有4 096种设计,工作量太大,不符合实际情况。采用优化拉丁方试验方法提取样本点,以较少的试验次数实现多因子多水平采样,同时可以保证样本点的均匀性。本次试验共取60组样本点,前50组样本点用于构建近似模型,后10组样本点用于近似模型精度误差的检验分析。

6 近似建模

采用响应面法构建近似模型。在众多响应面法中,多项式响应面法最为常用,核心理念是利用试验设计结果建立设计空间范围内的目标函数和设计变量间的近似数学表达式。多项式响应面法是一种试验设计结合数学建模的优化方法[12]。

用多项式响应面法构建多项式近似模型,目标函数和设计变量之间的函数关系为:

(1)

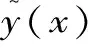
基函数阶数越高,响应面函数就越接近真实系统。

一般而言,三阶及以下多项式响应面法可解决实际应用中的大部分问题。三阶多项式响应面法构建的近似模型数学表达式为:

(2)

式中:βN+i为二阶偏移因数;β2N+i为三阶偏移因数;βij为交互作用因数;xi、xj为参数变量。

多项式响应面模型的最小样本数量仅取决于选择模型的阶数、输入变量的数量。在初始化时,三阶多项式所需要的最小样本数量为(N+1)(N+2)/2+N。

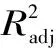
(3)

(4)

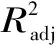
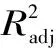
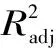
表3 近似模型精度指标

7 铺层角度优化设计

建立碳纤维复合材料机器人臂杆铺层优化数学模型,为:

findθi=[θ1,θ2,…,θ6]

minUj(θi),j=1,2,…,5

s.tθi[-45°,0°,45°,90°]

U1≤4.819×10-3

U2≤7.911×10-2

U3≤9.418×10-2

U4≤3.619×10-2

U5≤7.125×10-3

f>40

Hmax<1

(5)

式中:θi为机器人臂杆各层的铺层角度;Uj(θi)为机器人臂杆各工况下的最大变形位移函数;Uj为机器人臂杆各工况下的最大变形位移;f为碳纤维复合材料机器人臂杆的固有频率;Hmax为最大失效因子。

θi为离散性的设计变量,采用多目标遗传算法来对其进行求解,算法的目标空间内没有重复个体,更容易生成多种多样的解。另一方面,相邻繁殖的机制有助于解决存在多峰的多目标优化问题[13]。

在Isight软件中基于近似模型对铺层角度优化模型进行求解计算,在计算过程中,优化模型的目标函数始终保持数值相同的权重因子。确定遗传算法各参数数值,交叉概率、基因长度、遗传代数、变异概率、种群数量依次为0.6、24、20、0.08、400。通过优化设计,得到15组帕累托最优解。

通过对碳纤维复合材料机器人臂杆铺层角度进行优化设计,得到多种铺层设计方案。根据碳纤维复合材料铺层设计原则,对优化计算后得到的帕累托最优解进行筛选。铺层设计原则包括三方面[14]。

(1)一般性原则。中面两侧均衡对称铺设,铺层角度方向数在满足设计要求的情况下应尽量少。对于复杂受力情况下的结构,应使用0°、90°正交铺设或者-45°、45°成对铺设。

(2)铺层百分比。对于多方向铺层组成的结构,45°、0°、-45°、90°四个方向的铺层百分比均应不低于10%。

(3)铺层顺序。相同铺层角度在连续铺层时不应超过四层,用45°或-45°铺层隔开0°和90°铺层,结构主要受到弯曲时,外表面应选择±45°铺层,并且45°和-45°铺层应尽量靠近,以降低弯扭耦合。

根据上述原则,综合考虑性能指标,在15组帕累托最优解中进行筛选,最终选取的铺层角度为[-45°,0°,-45°,90°,45°,45°,45°,90°,-45°,0°,-45°]S。代入原模型,进行仿真,变形位移云图如图6所示。

对仿真得到的值与优化算法得到的值进行对比,结果见表4。由表4可以得出,仿真值与近似模型优化算法之间存在一定误差,其中工况二的误差最大,为0.61%,工况四的误差最小,为0.08%。综合来看,五种工况的误差都比较小。因此,多目标优化设计方法具有较好的准确性。

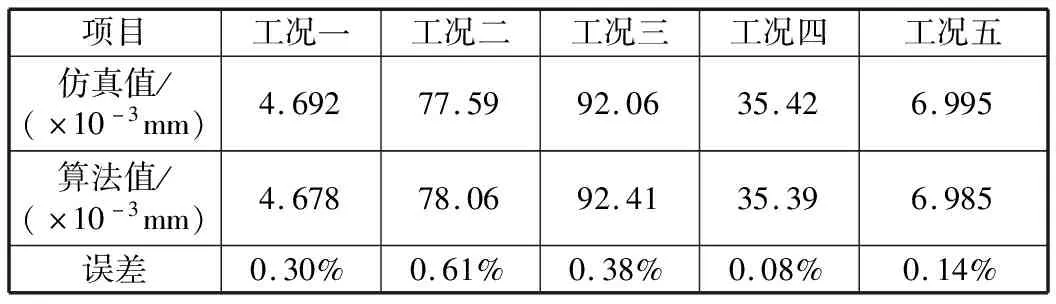
表4 最大变形位移结果对比

对优化前的准各向同性铺层方式与优化后得到的帕累托最优解铺层方式进行指标对比,结果见表5。由表5可以看出,优化后碳纤维复合材料机器人臂杆在各工况下的变形位移均有所减小。采用三维Hashin失效准则对优化后碳纤维复合材料机器人臂杆进行失效分析计算[15],结果表明,各工况下碳纤维复合材料机器人臂杆的最大失效因子均小于1,满足强度要求,质量与铝合金机器人臂杆相比减小了39.6%,提高了机器人臂杆的性能。

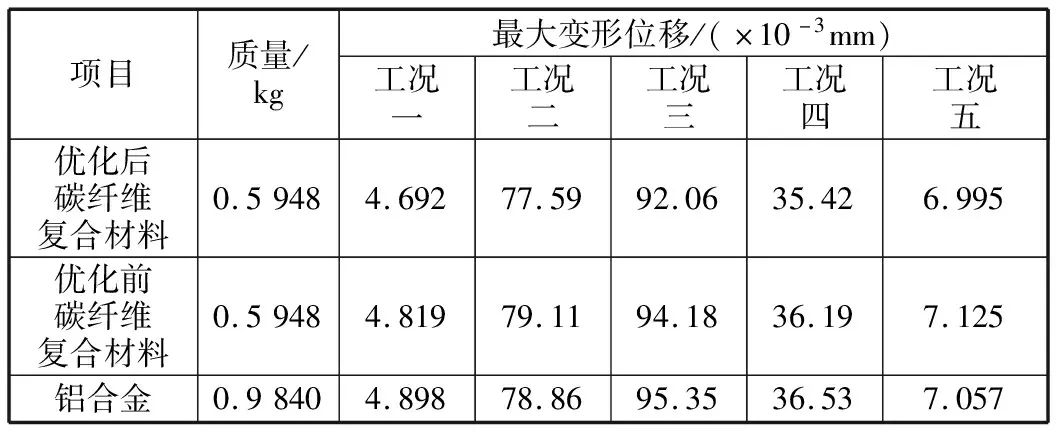
表5 机器人臂杆指标对比

8 结论

笔者对铝合金机器人臂杆和初始设计的采用准各向同性铺层方式的碳纤维复合材料机器人臂杆进行仿真分析,比较性能参数,确定碳纤维复合材料的铺层厚度。采用多目标遗传算法对铺层角度进行优化,在满足强度要求的前提下,使机器人臂杆的刚度得到较大提升,与铝合金机器人臂杆相比,质量减小39.6%,轻量化效果明显,为后续碳纤维复合材料在工业机器人中的应用提供了参考。