新型弯拉变形转换金属阻尼器抗震性能研究★
2021-12-13姜驭勋孟文盛
姜驭勋,孟文盛
(大连交通大学,辽宁 大连 116028)
1 概述
传统建筑结构主要靠结构自身变形吸收地震能量的输入,该行为将导致主体结构构件发生破坏,并造成重大的经济财产损失。阻尼器的设置可以有效耗散外部能量的输入,进而避免主体结构过早进入塑性变形状态,从而降低甚至避免主体结构的破坏。
典型的金属阻尼器装置往往通过其弯曲[1-2]、剪切[3-4]、拉伸压缩[5-7]变形进行屈服耗能。金属阻尼器通过其自身的塑性变形行为消耗外部能量,具有耗能能力强、力学性能稳定、数值计算方便、易于实现不同强度和刚度、制造成本低等优点,被广泛应用于实际工程结构的抗震设计中[8]。已有阻尼器的屈服变形行为往往均为单一的变形形式,其受载值达到屈服荷载后变形及承载能力则显著降低,无法再有效提升结构的整体抗震性能。本文提出一种新型弯-拉变形转换金属阻尼器,该阻尼器在低位移水平下发生弯曲变形进行屈服耗能,随着外部荷载的增加其变形机制由弯曲变形转换为拉伸变形,且承载力再次提高,进而使结构的二次抗震能力显著提升,研究该类金属阻尼器的抗震性能,具有极大的实际工程意义。
2 阻尼器设计及工作机理
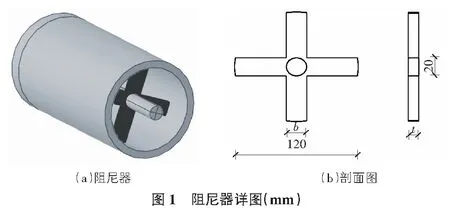
本文提出的弯-拉变形转换阻尼器主要包括外部高强钢管、十字形耗能钢板和中心处加载轴构成,见图1,其中b为耗能钢板宽度,取值分别为20.0 mm,22.5 mm和25.0 mm;t为耗能钢板厚度,取值分别为10.0 mm,12.5 mm和15.0 mm。鉴于耗能钢板的厚度和宽度对其抗震性能影响最为显著,因此本文共设置3种钢板厚度和3种钢板宽度加载工况,以便对阻尼器的力学性能进行参数化研究。
加载过程中,荷载作用于加载轴端部,施加往复位移荷载,低位移水平下十字形耗能钢板通过钢板的弯曲变形进行屈服耗能,当位移达到一定水平后,钢板变形机制则由弯曲变形转换为拉伸变形,并进行拉伸变形条件下的减震耗能。本文阻尼器加载轴和外部钢管采用Q345级钢,十字形耗能钢板采用Q235级钢,以此确保加载过程中仅阻尼器发生破坏,而非耗能构件免于破坏。
3 有限元模型建立
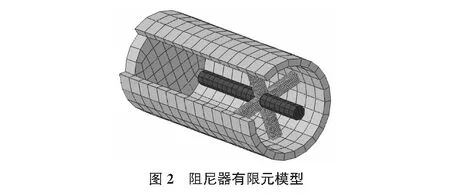
基于ABAQUS软件建立阻尼器的有限元模型,外部钢管、加载轴和十字形耗能钢板均采用八节点三维实体减缩积分单元C3D8R,钢管与耗能钢板焊接区域及加载轴与耗能钢板焊接区域均采用Tie命令进行绑定,以此保证两者间的变形协调,加载轴的受载端通过参考点进行刚体连接,其有限元模型如图2所示。阻尼器各组件材料均选用双线性随动强化本构模型。
4 力学性能分析
采用前述建立的有限元模型,加载轴端部施加低周往复荷载,本文采用位移控制的加载模式进行加载,计算得到各工况下阻尼器的荷载-位移滞回曲线如图3所示。
从滞回曲线可以看出,低位移水平下阻尼器展现出明显的弯曲变形屈服耗能,随着位移的增加,阻尼器的刚度和承载能力显著增强,其变形机制此时由弯曲变形向拉伸变形转换。针对阻尼器的耗能钢板厚度而言,随着钢板厚度的增加其承载能力不断提高,厚度为12.5 mm和15.0 mm的阻尼器相较于厚度为10.0 mm的阻尼器其最大承载力分别提高28.7%和47.6%。同时,随着钢板厚度的增加,阻尼器的屈服后刚度也有明显提升,滞回曲线更加饱满,所包围的面积更大,可见随着耗能钢板厚度的增加阻尼器的减震耗能能力逐渐增强。
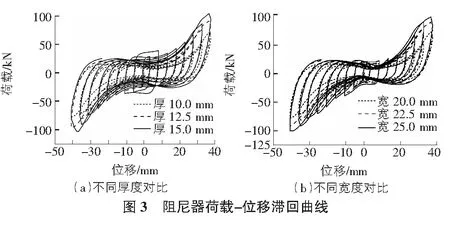
针对十字形钢板宽度的变化,从图3中可以看出,随着耗能钢板宽度的增加,阻尼器的承载力也有显著提高,宽度为25.0 mm和22.5 mm的阻尼器,其最大承载力相较于耗能钢板宽度为20.0 mm的阻尼器分别提高23.3%和36.2%。通过耗能钢板宽度和厚度对阻尼器承载能力的影响幅度可以看出,耗能钢板厚度对阻尼器承载能力的影响更加显著。同时,通过对比可以看出,随着耗能钢板宽度的增加,阻尼器的屈服后拉伸变形阶段的加载刚度提升幅度明显,卸载刚度受钢板宽度的影响变化不大。从耗能角度出发,可以看出随着钢板宽度的增加,滞回曲线更加饱满,其所包围的面积更大,耗能能力有所增强。
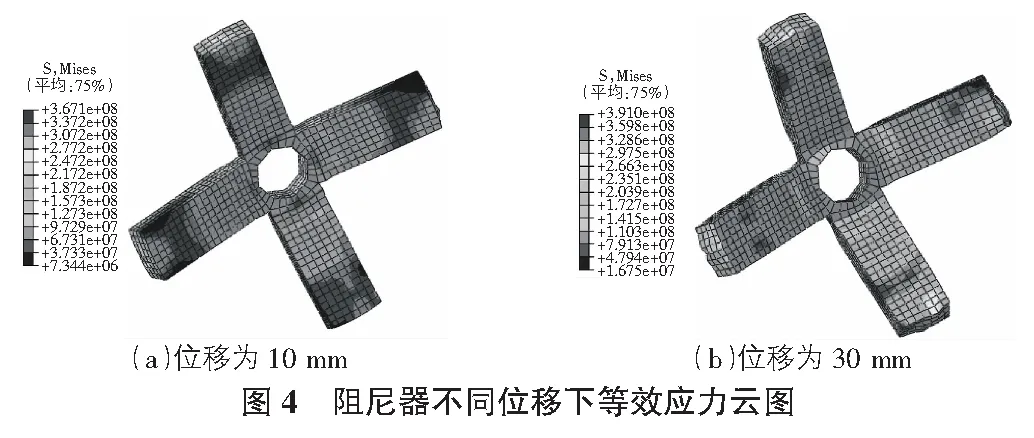
图4给出了宽度b=20 mm,厚度t=10 mm的阻尼器在位移为10 mm和位移为30 mm时的von-mises等效应力云。从阻尼器在不同位移加载阶段的等效应力云图可以看出,低位移水平线具有显著的弯曲变形特点,屈服区域更加集中,随着变形的进一步增加,达到拉伸变形阶段其耗能钢板的不同界面均发生塑性屈服,其屈服区域更加分散,耗能能力进一步增强。
5 结语
本文基于金属阻尼器的减震耗能特点提出了一种新型弯-拉变形转换金属阻尼器,通过数值模拟获得了以下结论:
1)该新型金属阻尼器在低位移水平下为弯曲变形,高位移水平下则转换为拉伸变形,其屈服后承载力、加载刚度在高位移水平下均显著提高。
2)随着耗能钢板厚度、宽度的增加,阻尼器的承载能力不断提高,其滞回性能显著提高,其耗能能力及屈服后刚度均有不同程度提高。
3)低位移水平下阻尼器耗能钢板的应力、应变分布更加集中,随着位移的增加其应力、应变分布更加均匀,体现出良好的拉伸变形性能特点。
