发展几何直观提升思维品质<br/>——《数图形的学问》教学

发展几何直观提升思维品质
——《数图形的学问》教学

2021-12-13文|周红

小学教学设计(数学) 2021年11期

关键词：向前走鼹鼠车票

文|周红

【教学内容】

北师大版四年级上册第93、94 页。

【教学过程】

一、激趣导入，引发探究

师：咱们的老朋友淘气在玩“鼹鼠钻洞”的游戏时，被一个问题难住了，我们一起去看看吧。

（课件出示主题图）

师：你发现了哪些数学信息？

生：有4 个洞口，任选一个洞口进入，向前走，再任选一个洞口钻出来。

师：你的观察力很强，一下子就能抓住问题的关键。如果按照这样的规则走，一共有多少条不同的路线呢？

师：直接说出答案似乎有些困难，那么请你认真思考：有什么好的策略来解决这个问题呢？

（学生独立思考、动手操作后与同伴交流）

生1：我是用画图的方法来解决这个问题的。我用4 个点A、B、C、D 分别表示4 个洞口，每两点之间的线段表示鼹鼠行走的路线。（如图）如果鼹鼠从A 洞口进入，向前走，任选一个洞口出来，分别可以从B、C、D 三个洞口出来，就有3 条路线，分别是AB、AC、AD 。

生2：我认为生1 说得不够全面，我想补充一下，他只说了从A洞口进入的情况，而题目中说任选一个洞口进入，所以鼹鼠还可以从B 洞口进入，向前走，路线有2 条，分别是BC、BD；从C 洞口进入的路线只有1 条CD，加上从A 洞口进入的3 条路线AB、AC、AD，合在一起应该是3+2+1=6（条）。

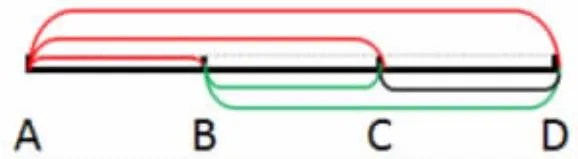
师：生1 同意生2 的说法吗？

生1：我同意，他的思考很全面，表达很清楚，既没有重复也没有遗漏。

师：能做到有序思考，清楚表达，很了不起，具备数学家的潜质，请同学们思考：从A 洞口进入，向前走的路线为什么是3 条呢？

生：因为一共有4 个洞口，从A 洞口进入向前走，只能从另外3个洞口出来，所以只有3 条路线。

师：这说明什么问题？

生：说明从第一个洞口引出的路线数是由洞口的总个数决定的，路线数比洞口总数少1，每往后一个洞口，依次减少一条路线。

师：这道题还有其他解法吗？

生：我也是用画图的方法解决的，但是我数路线的方法和他不一样。（如图）我先数最短的线段有3 条，是AB、BC、CD。接着数比较长的线段有2 条，是AC、BD。最后数最长的线段有1 条，是AD，所以一共也是6 条路线，列式为：3+2+1=6（条）。

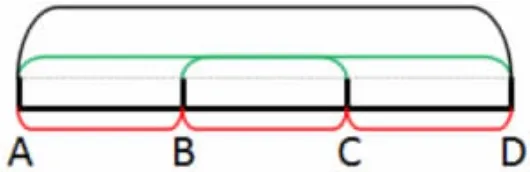
师：这个算式里的3、2、1 又分别表示什么呢？

生：因为题目中有4 个点，所以这里的3 表示最短的路线有3条，比较长的线段（2 条短线段组合的）有2 条；最长的线段（3 条短线段组合的）有1 条。

师：不论我们用哪种方法解决这个问题，都遵循了什么样的原则呢？

生：有序思考。

二、联系生活，发展应用

师：鼹鼠从洞里钻出来后，准备坐公交车去菜地旅行，现在已经到达了公交车站，它又遇到了什么问题呢？请看（出示主题图）——

师：你发现了什么？

生：一共有5 个车站，单程需要准备多少种不同的车票？

师：你是怎样理解单程票的？

生：单程票就是往一个方向的车票，本题中是从红薯站开往土豆站方向，只去不回就叫单程票。

师：理解得很深刻。有5 个车站，单程票一共有多少种呢？请同学们利用刚才的经验，画一画、数一数、算一算，并和同伴交流一下。

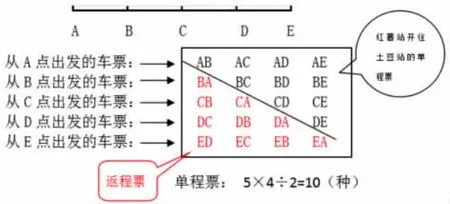
生1：我认为5 个车站，单程票共有10 种。我把5 个车站看成5 个点A、B、C、D、E，如图，先从A车站出发，开往E 车站的单程票共有4 种，分别是AB、AC、AD、AE；同理，从B 车站出发，开往E车站的单程票共有3 种，分别是BC、BD、BE；从C 车站出发，开往E 车站的单程票共有2 种，分别是CD、CE；从D 车站出发，开往E 车站的单程票只有1 种，是DE，再把它们加起来4+3+2+1=10（种），所以一共需要准备10 种不同的单程票。

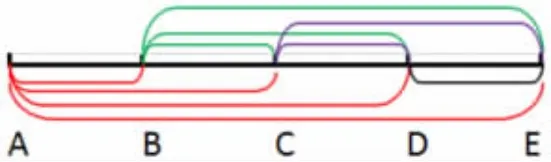
生2：老师，我和生1 的数法不一样，我先数只有一站路的单程票，共有4 种，分别是AB、BC、CD、DE；接着数含有两站路的单程票共有3 种，分别是AC、BD、CE；再数含有三站路的单程票共有2 种，分别是AD、BE；最后数四站路的单程票,有1 种，是AE。列式为：4+3+2+1=10（种）。

师：同学们在解决问题时，都做到了有序思考，已经具备了良好的思维品质。想一想，还有没有其他的方法来解决这道题呢？

生3：我的方法是5×4÷2=10（种）。

师：说来听听，你是怎么想的？

生3：一共有5 个车站，把这5 个车站看成5 个点A、B、C、D、E。如图所示：从每个点（车站）到其他4 个点（车站）都有4 种车票，5 个点（车站）共有4×5=20（种）不同的车票，其中有一半（左下部分）是返程票，所以要用20÷2=10（种），有10 种单程票。如果是求往返的车票共有多少种，直接用4×5=20（种）就可以了。