复合绝缘子泄漏电流仿真计算
2021-12-13王健宏刘程
王健宏 刘程
(广东电网有限责任公司汕头供电局,广东汕头 515000)
目前国内外对绝缘子伞裙破损的研究主要针对于强风导致伞裙根部撕裂、材料老化芯棒裸露后断裂掉串等情况,而对鸟类活动导致绝缘子破损的情况研究甚少。针对此现象本文主要研究鸟啄绝缘子致其破损情况下的电流在复合绝缘子内部的传导性状,本文通过建立复合绝缘子的ANSYS 三维有限元模型,首先以复合绝缘子不同破损程度和不同破损位置为变量,模拟了鸟啄绝缘子致其破损的不同程度、不同位置,然后对复合绝缘子泄漏电流的矢量值进行分析计算,得出在不同情况下泄漏电流密度分布图以及相应数据[1-4]。
1 建立复合绝缘子模型
复合绝缘子泄漏电流分析计算模型中包括复合绝缘子伞裙、护套、内部芯棒以及作为电极的绝缘子串端部连接金具。在保证计算可靠性的前提下,本文假定:在以破损为单一变量时,假设复合绝缘子处于干燥、清洁的自然环境中,且硅橡胶伞裙上没有污秽和水分;由于空气电阻率远远大于固体物质,在计算绝缘子内部泄漏电流时忽略空气对绝缘子的影响,因此不添加空气域。
2 泄漏电流仿真计算结果分析
由电流密度分布的仿真结果可以看出,绝缘子硅橡胶伞套部分电流密度平均值为1.02×10-8A/mm2,在伞套伞裙接触截面上及高压端局部会达到2.01~6.02×10-8A/mm2,而绝缘子内部芯棒的电流密度分布则不超过0.549×10-8A/mm2,同时复合绝缘子伞裙上的电流分布不超过0.669×10-8A/mm2,其分布规律为高压端伞裙上的电流密度略大于低压端伞裙,同时越接近伞裙边缘,电流密度越小。
通过图1 可以更直观的看出内部绝缘子电流密度的分布状况,在稳态电压下,区域电流密度最大矢量值为1.51×10-8A/mm2,出现在高压端连接金具附近。在伞裙与伞套圆柱体交界处,电流密度激增,且在伞裙上表面与伞套柱体交界处的泄漏电流值要高于伞裙下表面,而在远离伞套柱体的绝缘子伞裙上的大部分区域电流密度分布趋近于零。并求出电压加载面至零电位面之间的电流,即为复合绝缘子的泄漏电流值,其结果如表1 所示。

表1 FXBW4-10/70 绝缘子泄漏电流值
3 复合绝缘子伞裙破损状态下泄漏电流仿真计算
针对绝缘子伞裙不同破损程度的泄漏电流仿真计算,本文建立了四种模型:其中模型Ⅰ为伞裙完整复合绝缘子,伞裙及其他部位均不存在缺陷;绝缘子Ⅱ,Ⅲ,Ⅳ高压端第一片伞裙尖端处存在缺损,破损自尖端开始,表现形式为伞裙半径减小。
3.1 伞裙不同破损程度对绝缘子泄漏电流的影响
本文在计算绝缘子破损情况下泄漏电流时选取了沿伞套表面、芯棒表面、芯棒中心三个距离为干弧路径,路径长175mm,每条路径上取40 个样本点,以这些点上的电流密度值为样本,绘制出该路径上的电流密度分布曲线,并得出不同破损程度下的曲线对比图。(图2~4)
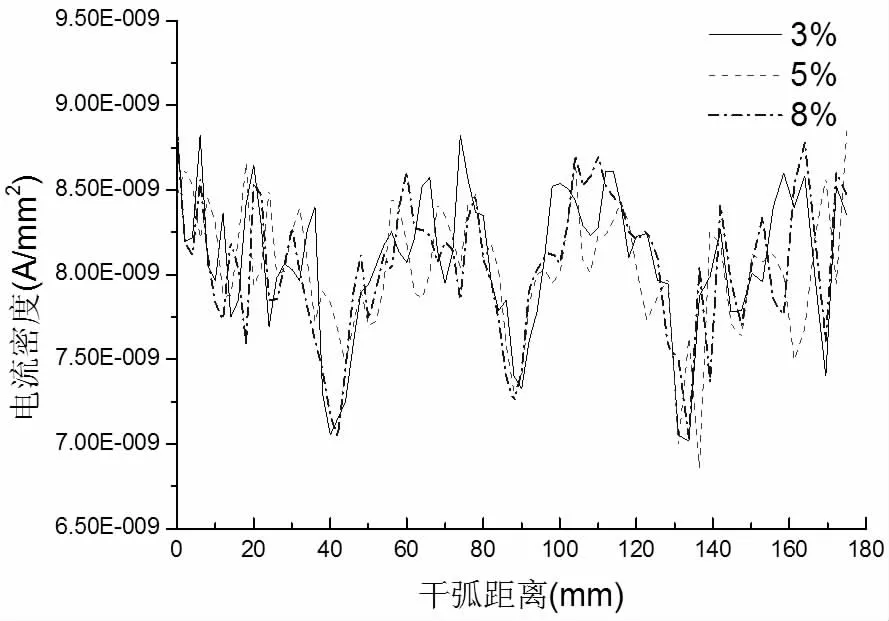
图2 不同破损程度伞套外表面干弧路径电流密度分布

图3 不同破损程度芯棒与伞套交界处干弧路径电流密度分布
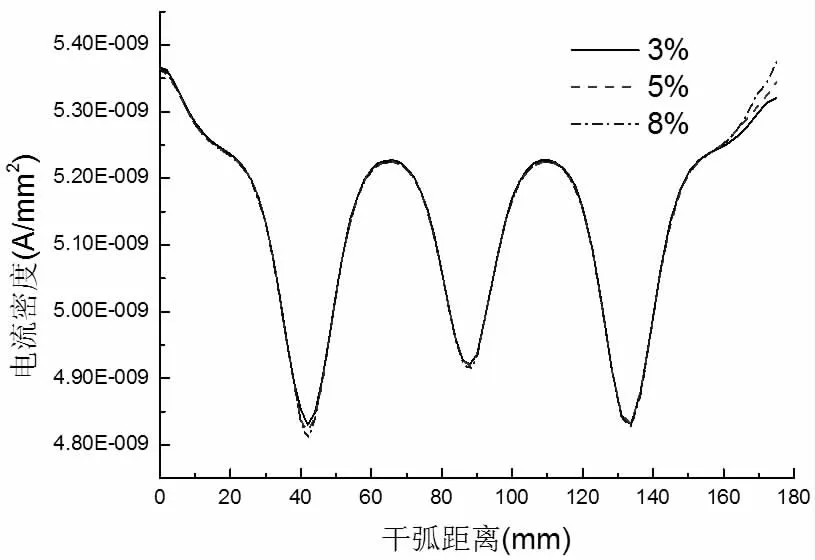
图4 不同破损程度芯棒中心干弧路径电流密度分布
从图2~4 可以看出,外柱体外表面的电流密度平均值1.05×10-8A/mm2,芯棒外表面与伞套交界处电流密度平均值约为8×10-9A/mm2,芯棒中心路径上的电流密度平均值约为5.2×10-9A/mm2,因此电流密度分布顺序为:伞套表面>芯棒表面>芯棒中心,即在不考虑伞裙的情况下,复合绝缘子电流密度分布外部高于内部。
表2 为不同破损程度时泄漏电流有限元积分命令计算所得结果,包括X、Y、Z 三个方向的电流密度积分以及积分矢量和。

表2 不同破损程度泄漏电流对比表
由表中数据可知,在破损程度为单一变量的情况下,复合绝缘子泄漏电流仿真值随破损程度增加略有上升趋势,变化幅度同理论计算的幅值相似,但略大于理论结果,幅值为2.01%左右,但相较于总量来说,泄漏电流增幅仍然很小,远远没有达到泄漏电流警戒值50mA,因此系统此时仍处于安全运行状态。在对不同方向上的泄漏电流积分仿真值记录可知,仅Y 方向(电流传输方向)与破损程度存在正关联度关系,其余方向由于受到网格划分,有限元计算误差等影响,与破损程度无直接比例关系,其正负号受到方向设定影响,并不代表实际大小。
3.2 伞裙不同破损位置对绝缘子泄漏电流的影响
图5、6 分别为中部破损和根部破损复合绝缘子表面泄漏电流分布云图。从图中可以看出,无论哪种破损对表面泄漏电流分布的影响都是比较微小的,其分布规律都是以芯棒和硅橡胶柱体为主,伞裙上分布较稀疏,且在伞裙与柱体交汇处,泄漏电流分布局部畸高,从矢量图中也可看出在交汇处将出现泄漏电流集中现象,这也说明电弧放电易产生于柱体与伞裙界面交汇处。对不同破损而言,由于根部破损导致交汇处形状突变,因此泄漏电流畸高点也发生变化,从根部破损云图中可以看出,高压端伞裙根部泄漏电流畸高点将随破损缺失部分而上移,最大密度0.2×10-7A/mm2出现在距高压端42mm 处,而高压端伞裙中部破损则不会出现这种现象,同无破损情况相同,泄漏电流最大密度出现在距离38mm 处,这说明根部破损对泄漏电流变化影响较其他两种破损大,且距低压端更近,因此需要额外注意伞裙根部破损情况,它可能造成泄漏电流畸高分布平面上移。

图5 中部破损模型泄漏电流分布云图

图6 伞裙下表面根部破损泄漏电流分布云图
在对不同破损程度进行分析时,芯棒外表面的路径上电流密度分布曲线振荡较剧烈且不规律,因此在对伞裙不同破损位置的泄漏电流仿真结果进行分析时,仅取伞套外表面路径和绝缘子芯棒中心路径绘制分析,结果见图7、8。
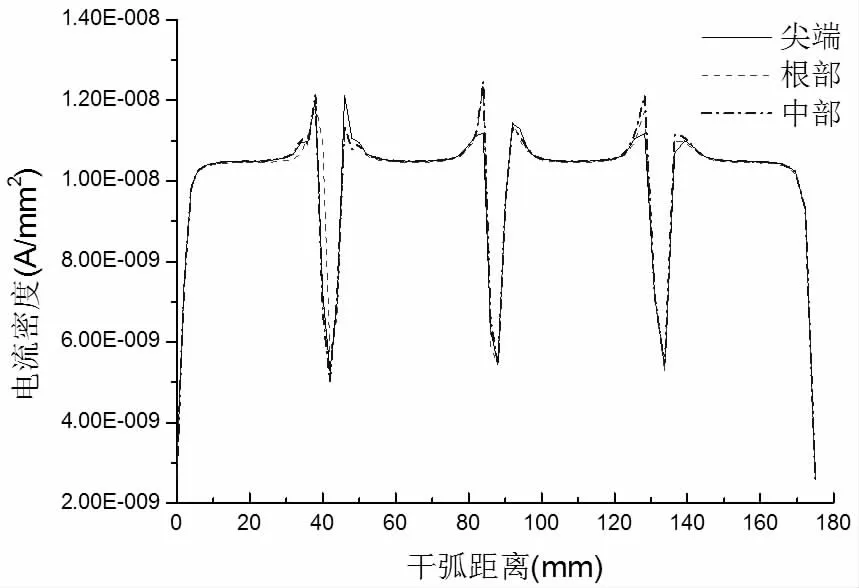
图7 不同破损位置伞套外表面干弧路径电流密度分布

图8 不同破损位置芯棒中心干弧路径电流密度分布
对下表面不同破损缺陷位置造成的绝缘子表现电流密度变化以及整体泄漏电流值进行积分运算(Integrate results),求出电压加载面至0 电位面之间的电流,即为泄漏电流值,与理论值进行比较,其结果见表3。

表3 不同破损位置泄漏电流对比表
由表中数据可以推得,与不同破损程度结果分析相似,在变量为不同破损位置时,泄漏电流仿真值增幅较理论值大,且理论计算得出的尖端破损时泄漏电流增幅最大,仿真结果表明根部破损时,泄漏电流最大,这是由于理论计算仅考虑伞裙半径尺寸的改变,而没有考虑到根部破损带来的泄漏电流畸变分布线上移的影响,导致伞裙半径减小后的整体电阻降低大于根部破损,且在理论计算中很难将电气性能的变化全部考虑到,因此还需要根据实际经验或试验结果,将调节值化作理论公式参数,使理论计算更加精确。
4 结论
通过建立完整洁净干燥情况下的复合绝缘子三维模型,进而建立不同破损程度和不同破损位置有限元模型,进行有限元分析,得出相应状态下的泄漏电流仿真结果,通过与理论值的对比,验证理论公式正确性,本章的主要结论如下:
4.1 仿真结果表明,复合绝缘子完整、干燥、洁净条件下,泄漏电流矢量积分和为4.39×10-5A,比理论值高11.7%,属合理误差范围内,说明理论计算公式具有一定参考价值。
4.2 高压端伞裙尖端不同破损程度仿真结果表明,复合绝缘子泄漏电流仿真值随破损程度增加略有上升趋势,随着破损程度从0%增加至8%,泄漏电流增幅为2.01%左右,远远没有达到泄漏电流警戒值50mA,系统此时仍处于安全运行状态。
4.3 通过对三条路径上的电流密度分布取值可得,外柱体外表面的电流密度平均值1.05×10-8A/mm2,芯棒外表面与伞套交界处电流密度平均值约为8×10-9A/mm2,芯棒中心路径上的电流密度平均值约为5.2×10-9A/mm2,因此电流密度分布顺序为:伞套表面>芯棒表面>芯棒中心,即在不考虑伞裙的情况下,复合绝缘子电流密度分布外部要高于内部。
