具有复杂围护结构光学窗口的传热特性分析

2021-12-13潘虹宇李佳奇夏新林

宇航学报 2021年10期

潘虹宇，李佳奇，陈学，夏新林

(哈尔滨工业大学能源科学与工程学院，哈尔滨 150001)

0 引言

探测系统作为飞行器的“眼睛”，包括卫星探测器、航空飞机探测器或弹载探测器等[1]。光学窗口是保护探测、成像仪器以及内部装置的关键部件，对于整个探测系统至关重要[2]。不仅可以将探测系统内部装置与外界环境隔离开，防止外部环境的杂质或气体进入。而且可以起到隔热的作用，减少外部高温环境对于探测装置探测精度的影响[3]。高速飞行器，如高速导弹、火箭等在其高速运动时会产生高温气动热流[4-6]，对光学窗口有显著的加热效果，使窗口温度上升至足以影响探测装置的水平。因此，对高速气动热流加热下的光学窗口高温瞬态传热特性的分析不容忽视。常见的窗口材料包括石英(SiO2)、蓝宝石(Al2O3)以及金刚石(C)等[7-8]。其中，石英和蓝宝石的应用最为广泛，两者因光谱的透过区间差异，常应用于可见光波段和红外波段探测系统。

许多学者的研究模型为系统整体，大多没有将光学窗口作为研究主体对象进行瞬态温度响应模拟计算[9-14]。针对光学窗口的瞬态温度场的辐射-导热耦合[15]计算仅仅开展了一部分的研究。许明明等[17]通过Workbench针对真空相机的光学窗口进行了热光学分析，研究了不同窗口厚度下的热形变。朱冉等[18]通过SolidWorks针对空间太阳望远镜光学窗口进行了稳态温度分布的模拟，并考虑了外部热流(太阳辐射)加载。张彪[19]基于Fluent混合编程针对光学窗口内的辐射-导热耦合换热进行了研究，采用有限体积法对辐射传输进行了计算。李一涵等[20]说明了高超声速飞行器光学探测窗口在高温下会发生辐射特性的变化，并且模拟了温度对于光学窗口透过率的影响。这是一种十分重要的现象，因此，本文针对具有光谱选择性的光学窗口的传热特性进行了研究。在以往关于光学探测系统的模拟计算中，对于包含复杂结构的系统模型，为了提高效率，节约计算资源，往往将其中的光学窗口近似作为不透明体或灰体进行处理。但是，采用如上方式处理时，忽略了其半透明特性以及光谱特性，对于光学窗口温度响应的计算不够精确，与真实工作情况相比会出现较大偏差。

本文将光学窗口按照具有光谱选择性的半透明体处理。首先，建立光学窗口以及复杂围护结构的数学物理模型；然后，整体采用辐射-导热耦合计算模型进行计算；最后，分别分析了半透明特征、光谱选择性、外部高温瞬态热流以及窗口尺寸对窗口瞬态传热特性的影响。

1 数学物理模型

光学窗口及复杂围护结构的几何模型如图1(a)所示。其中，光学窗口部分为圆台形状,如图1(b)中所示，窗口材料采用石英(SiO2)。采用有限体积法(FVM)对导热过程进行计算，离散坐标法(DOM)对辐射传热过程进行计算。针对模型中存在的辐射-导热耦合传热现象，假设光学窗口及围护结构材料均匀、各向同性，在模拟的过程中不考虑对流传热。模拟计算时使用的控制方程如下所示：

1)围护结构部分的瞬态导热方程[21]为：

(1)

2)光学窗口为半透明吸收性介质，其辐射-导热耦

图1 数值计算的物理模型Fig.1 Physical model of numerical calculation

合传热方程[22]为：

(2)

式中:T为温度；τ为时间；ρ为密度；c为比热；λ为导热系数；qr为辐射热流。其导热系数为1.7 W/(m·K)，比热容为1000 J/(kg·K)，密度为2200 kg/m3。

3)半透明吸收性介质内部辐射传输方程[22]为：

(3)

式中:Iλ(s)为在s位置的光谱辐射强度；kαλ为光谱吸收系数；Ibλ(s)为在s位置的黑体光谱辐射强度。所采用的光学窗口的光谱物性参数为本课题组利用实验测量的光谱物性参数[23]，并对其进行了谱带近似[24]。

2 模型验证

2.1 网格无关性验证

针对划分网格数为284039、94199、62792的三种情况，进行了模型温度响应的计算。如图2所示，网格数达到62792后，继续增加网格数，计算结果差异可以忽略。因此，验证了计算模型的网格无关性，并仅需要划分62792个网格即可得到精确的计算结果。

图2 不同划分网格数下的温度响应对比Fig.2 Comparison of temperature responses with different grid number

2.2 辐射-导热耦合传热模型验证

使用如图3所示模型对辐射-导热耦合传热模型进行验证。高度L与半径R的比例为2，即L=2R，将圆柱模型看作半透明参与性介质，衰减系数β=1 m-1，底面温度Tref为其他各面温度Tc的两倍，即Tref= 2Tc，且各壁面均为漫反射黑体壁面。模型的辐射-导热系数N由下式定义：

(4)

图3 圆柱体模型示意图Fig.3 Illustration of cylinder model

如图4所示，与文献[26]进行对比，结果吻合良好。可以证明本文所使用的辐射-导热耦合传热计算模型的准确性。

图4 不同辐射-导热系数中心轴线温度的对比Fig.4 Comparison of radiative-conductive coefficient N on centerline temperature

3 计算结果分析

为精确评估光学窗口的传热特性，对窗口的瞬态温度响应进行了计算。采用Fluent进行数值模拟，使用了DOM辐射传输计算方法。将该模型划分为62792个网格，时间步长选取为0.1 s。

在将半透明窗口当作黑体或灰体处理时，忽略了半透明介质所具有的光谱选择性。半透明介质的光学物性在不同波段下并不完全相同，有时甚至相差较大。因此，为计算考虑窗口的光谱选择性的瞬态温度响应，并进行相应的分析,本文将全光谱范围划分为4个谱带进行计算[24]，各个谱带的光学窗口物性参数见表1。为表征窗口的温度响应，选取光学窗口中心轴向位置A(z=6.5 mm)、B(z=10.5 mm)、C(z=14.5 mm)、D(z=18.5 mm)四点作为模型整体温度响应的特征点。

表1 窗口介质的光谱物性参数Table 1 Spectral optical properties of window

3.1 窗口光学物性影响

在精度要求不高的工程计算中，为简化计算常常将光学窗口作为具有固定发射率的不透明体进行处理。采用该方式处理时，选择D点温度作为特征点。由于石英窗口在低温时发射率较低，而在高温时发射率较高。因此，将光学窗口的发射率分别假设为0.05与0.95，计算模型的温度响应。与灰体处理和考虑光谱选择性时的计算结果进行对比。

图5 光学窗口按灰体处理与不透明体处理时，外表面中心点温度响应对比Fig.5 Comparison of temperature response at window outer surface center between grey-body treatment and opaque body treatment

对比结果如图5所示。在初始阶段，各个工况的温度差异不明显，随着时间增加，温度差异也逐渐增大。在温度最高时刻，按固定发射率0.05与0.95的不透明体处理时，忽略了其半透明特征，温度峰值分别增大了235.72 K和减小了114.78 K，此时误差为22.7%和11.1%。误差最大时，分别可达31.4%与12.4%。

按半透明灰体处理时，忽略了光谱选择性，相比考虑窗口介质的光谱选择特性， A、B与C、D四点的瞬态温度响应的对比情况如图6、图7所示。两种工况的温度变化趋势基本相似。在计算的初始阶段温度差异很小，随着时间增加逐渐增大。约200 s后，各点的温度差异就十分明显了。因此，需要对温度差异大小进行进一步的评估。

考虑窗口介质光谱特性与不考虑时相比，最高峰值温度下降了316.83 K，温度偏差约占此时刻温度的30.5%，但温度最高时刻没有变化，仍旧为τ=355.6 s时。温度差异ΔT最大为τ=390.0 s时，ΔT=327.84 K，温度偏差约占此时温度的40.4%。因此，若想对光学窗口的温度响应精确地计算，应该同时考虑到窗口的半透明特征以及光谱选择性。

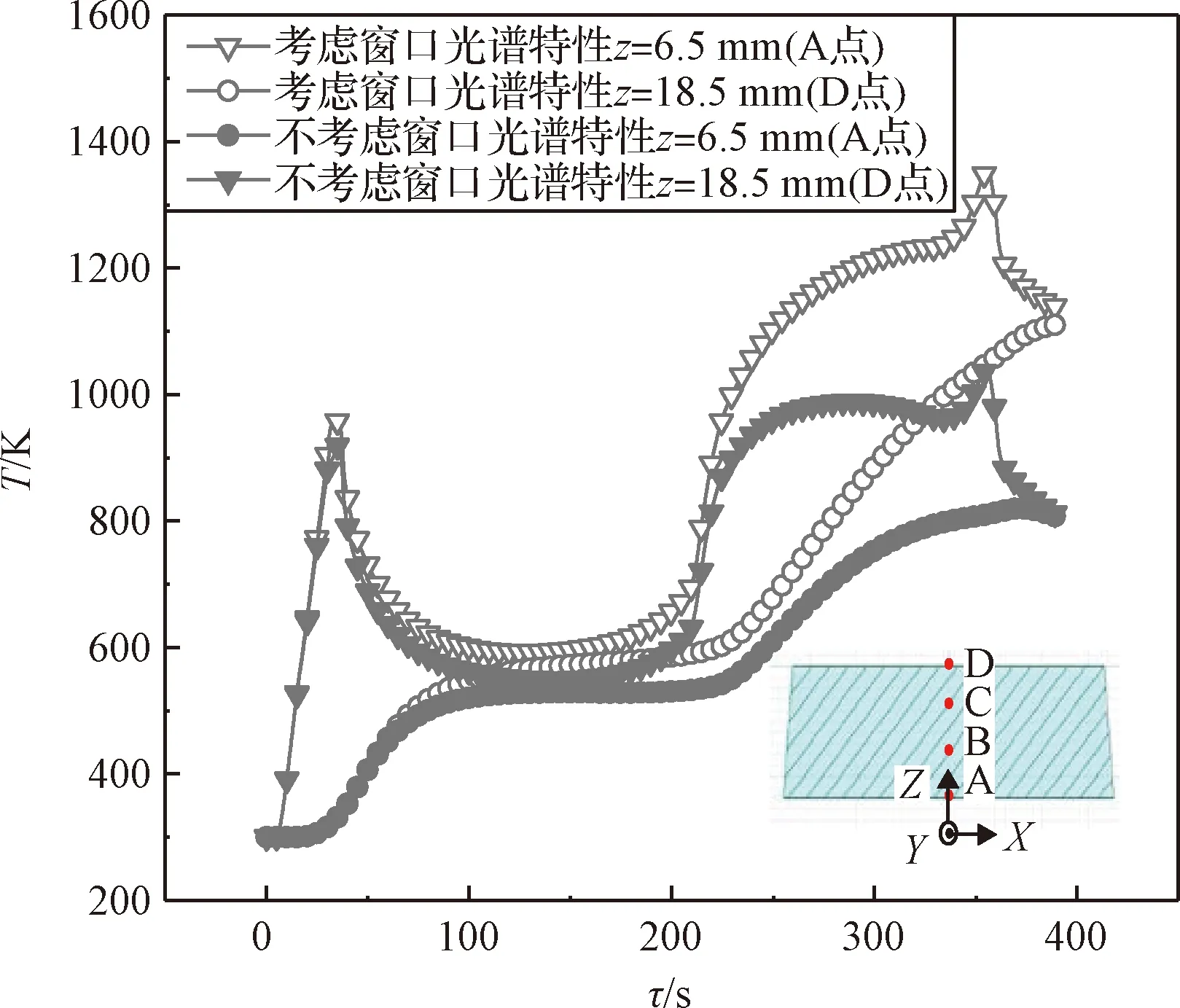
图6 窗口表面A、D两点的温度响应的对比Fig.6 Comparison of temperature response at window surface points A and D

图7 窗口内部B、C两点的温度场的对比Fig.7 Comparison of temperature responses at window inner points B and C

3.2 窗口及围护结构的瞬态温度场分析

根据以上对比，考虑窗口半透明特征与光谱选择性，进行了温度响应分析。不同位置处温度随时间的变化曲线如图8所示。D点温度随时间变化较为剧烈，主要原因是受到外部的高温热流直接加载影响，温度变化趋势与瞬态热流变化趋势接近。在计算过程中，共存在两个温度峰值，分别位于时间τ=32.9 s、τ=355.6 s时，温度峰值分别为925.25 K、1038.63 K。

根据图8中温度响应曲线，光学窗口的整体温度响应主要可以分为四个阶段。第一阶段，由于受到外部热流加热，窗口温度迅速升高，直至第一个峰值(τ=32.9 s)；随后由于窗口向围护结构导热以及加热热流的急剧减小，温度开始下降，逐渐达到一个较为平稳的阶段，在该阶段各个特征点温度也非常接近；温度在200.0 s左右时，由于加载热流的上升，温度也开始迅速上升至第二个峰值(τ=355.6 s)，也是温度的最大值；最后阶段，热流结束加载，窗口冷却后温度略微下降。C点处与D点处曲线变化趋势大致相同，也有两个峰值和一个温度值较低且平稳的阶段；A点、B点处温度总体呈现出上升趋势，仅中间出现一个温度平稳的阶段。

图8 光学窗口中心特征点处温度响应Fig.8 Temperature response of several characteristic points at optical window center

图9为三个不同时刻τ=32.9 s、149.5 s、355.6 s的温度场分布。如图9所示,以最外侧表面的特征点D为例，τ=32.9 s时，由于受突增热流加热影响温度较高，热量通过导热和辐射方式向窗口内部传输，达到第一个峰值925.25 K。在窗口厚度方向上温度递减,窗口内部温差最大600.60 K。随后，在τ=149.5 s时，由于热流的减小，热量逐渐扩散，温度处于较为平稳的低谷阶段。窗口内部温度较为均匀，均550 K左右。τ=355.6 s时，达到第二个峰值处，温度达到最大值1038.63 K，此时窗口内部最大温差为228.22 K。

3.3 外部加载热流影响

由于在实际应用中光学窗口常常面临着高速气动加热的问题，故而研究了不同大小的外部瞬态高温气动热流加载下，光学窗口产生的瞬态温度响应。选择0.5倍q、1倍q、2.5倍q三种气动加热热流进行数值计算。

结果如图10所示，以D点的温度响应作为参考，随着瞬态热流q增大，温度迅速上升。0.5倍q加载时，两个温度峰值分别位于τ=32.9 s及τ=356.1 s，大小为621.42 K及739.92 K，相比1倍q温度峰值下降了最多300 K左右，约为32.9%；2.5倍q加载时，两个温度峰值分别位于τ=32.2 s及τ=355.3 s，大小为1723.44 K及1594.71 K，相比1倍q温度峰值升高了最多700 K左右，约为86.3%。

当气动热流达到2.5倍q时，由于外部热流的剧烈加热，温度升高十分迅速。冷却后温度下降也同样迅速，再次加热达到的第二个峰值温度要略低于位于第一个峰值温度。因此，温度最大值变为了第一个温度峰值处。

图9 模型中心截面不同时刻的温度分布Fig.9 Temperature distributions of the section at the center of the model at various times

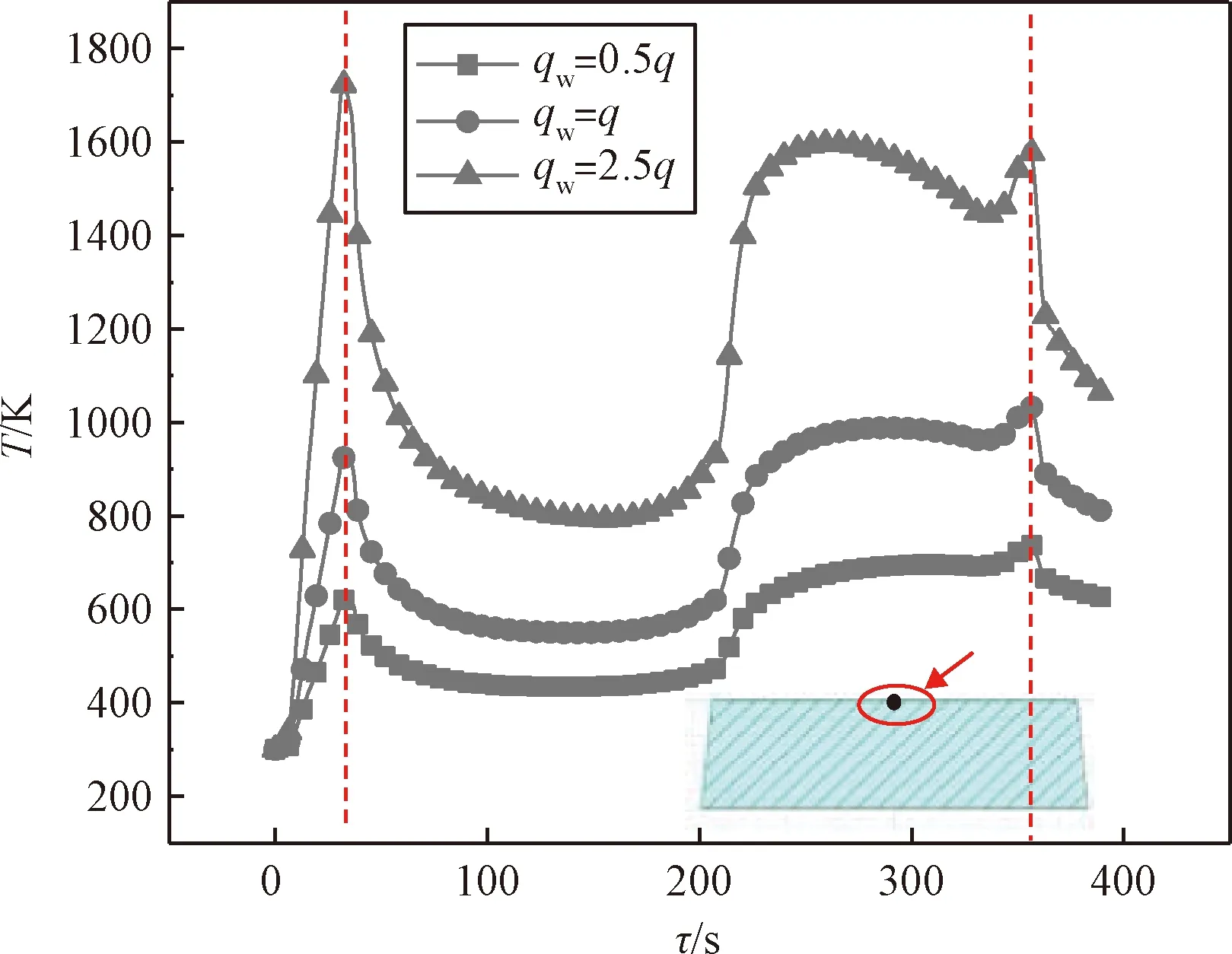
图10 光学窗口在不同高温气动热流加载下的温度响应Fig.10 Comparison of optical window’s temperature response with different high-temperature pneumatic heat flux loading

3.4 窗口尺寸影响

研究光学窗口的不同尺寸对其温度响应的影响，分别选取了半径r=35、25 mm,厚度d=15 mm；半径r=35 mm，厚度d=10 mm三组工况进行了温度响应的计算，并选取A、D两点的温度响应进行分析。

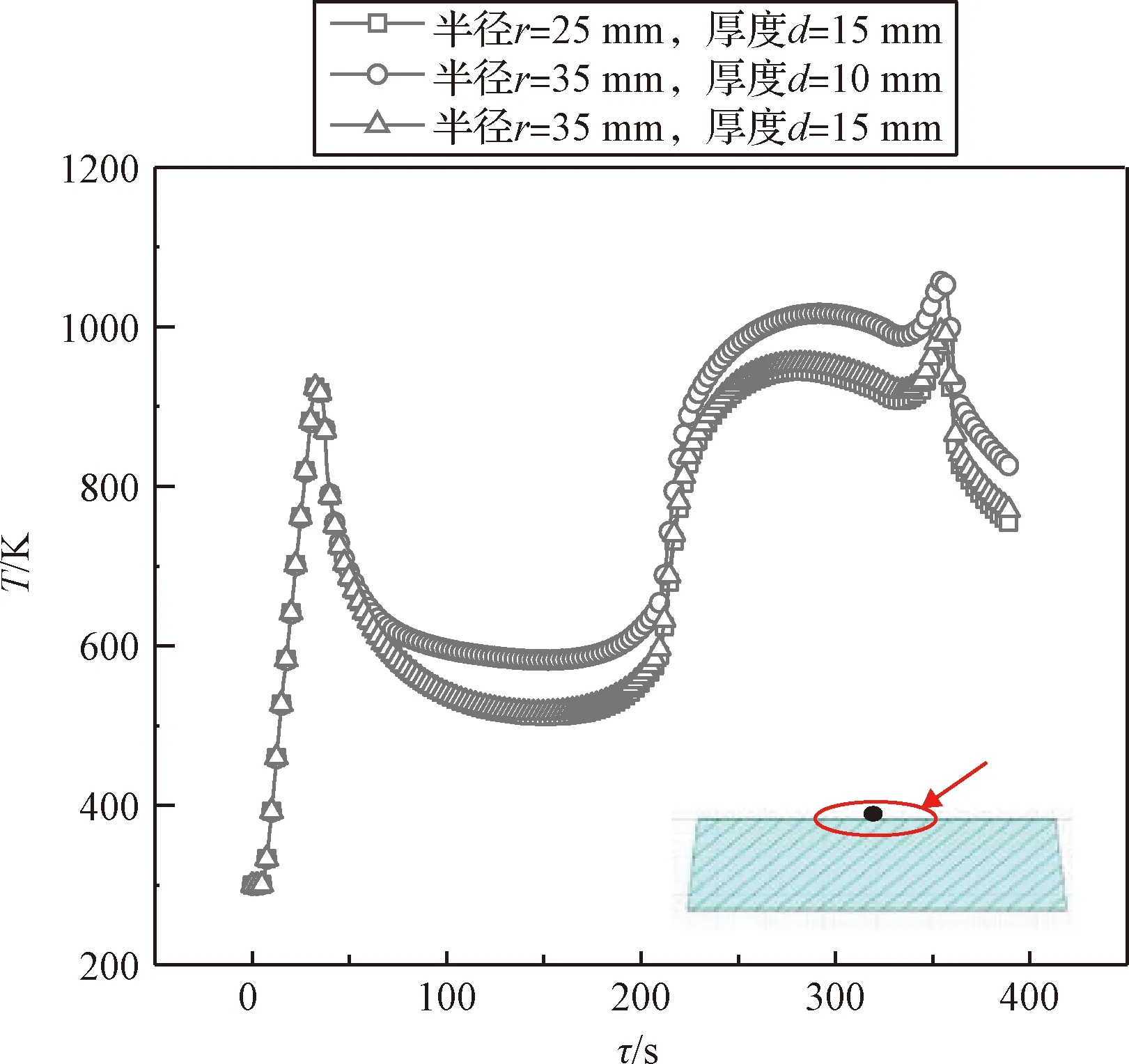
图11 不同几何尺寸的光学窗口外表面D点的温度响应Fig.11 Comparison of temperature response of point D at outside surface in different geometric dimensioning optical window

图12 不同几何尺寸的光学窗口内表面A点的温度响应Fig.12 Comparison of temperature response of point A at inside surface in different geometric dimensioning optical window

结果如图11、12所示，随着窗口半径的增大，两条曲线非常接近，温度响应差异非常小；但是，随着窗口厚度的增大，两条曲线出现明显差异，内外部温度响应会减小。随着半径增大，温度最大上升31.80 K，约占7.8%。其原因为窗口半径仅仅对径向的传热特性有影响，而对于窗口轴向的传热特性几乎没有影响。因此，温度响应变化很小。厚度增大时，温度最多下降183.64 K，约占30.2%。其原因为加热热流作用于整体模型的上表面，随着窗口厚度的增大，沿轴向的传热特性受到较大影响，尤其是其导热效果受到削弱，导致温度响应有所下降；同时，其光学厚度也随厚度增大了，使得窗口对辐射的吸收效果增强，故外部D点温度响应的降低程度相比于内部A点较小。