空间机器人抓捕碰撞分析与轨迹规划镇定控制

樊 茂，汤 亮,2

(1. 北京控制工程研究所，北京 100190；2. 空间智能控制技术重点实验室，北京 100190)

0 引 言

近些年来，空间机器人在空间操作方面得到了广泛的应用[1-3]，例如国际空间站的组装[4]、哈勃望远镜的维修[5]以及国际空间站货运仓的交会对接等空间操作都是空间机械臂的经典应用场景。但是随着空间操作任务需求与难度的不断提升，空间机械臂也面临着对废弃卫星、空间碎片与小型陨石等非合作目标的抓捕问题[6]。在抓捕非合作目标的过程中，机械臂末端与被捕获目标进行接触碰撞，为了增大抓捕过程的成功率，在抓捕过程中需要关闭基座的姿态控制系统，因此抓捕产生的碰撞冲击会对空间机器人系统造成冲击[7]，严重时甚至会造成抓捕目标后所形成组合体的翻滚、失稳；除此之外，抓捕过程对机械臂系统产生的冲击会带动机械臂一起运动，为了消除抓捕后机械臂受到的冲击效应，有必要设计相应的控制策略，在减小碰撞冲击的同时维持目标与平台之间的相对稳定，避免系统失稳。

针对抓捕目标后组合体受到的冲击问题，许多学者提出了不同的方法来实现对组合体系统的镇定控制[8-11]。为了减少机械臂控制过程中对平台姿态的扰动，文献[8]利用零反作用操作在日本空间机器人ETS-VII上进行了在轨实验，该方法有效减少了机械臂在运动时对卫星姿态的影响，同时还降低了由于约束反力带来的关节角速度限制。文献[9]对碰撞前的机械臂构型及轨迹进行优化，实现了机械臂碰撞脉冲力的最小化。文献[10]研究了航天器抓捕目标后，系统质量发生变化所引起的失稳问题，提出了关节阻尼控制策略和关节函数参数化协调控制方法，对碰撞后状态发生突变的系统进行了基于角动量守恒的协调控制。文献[11]用递推最小二乘算法在线估计目标角动量，利用角动量守恒定律提出了自适应零反作用空间算法，减少了机械臂运动对平台姿态的影响。

虽然以上学者都利用基于角动量守恒的零反作用空间算法进行机械臂关节的轨迹规划，但所提出的方法都只以减少对卫星平台的扰动为目标，忽略了初始角动量对系统的影响，因此许多学者转而利用优化算法求解机械臂运动轨迹[12-18]。文献[12]提出了基于混沌粒子群算法的关节空间点对点轨迹规划方法，该方法考虑了机械臂运动过程中对卫星平台的反作用轨迹规划问题。文献[13]将机械臂轨迹用七次多项式的正弦函数参数化，利用空间机器人的非完整特性提出了同时考虑机械臂末端与平台基座扰动的点对点轨迹规划方法。文献[14-15]对抓捕目标的消旋路径进行了设计，利用优化算法求解得到同时考虑末端接触力矩与阻尼时间的轨迹。文献[16]提出了基于角动量转移的优化方法，利用粒子群算法设计了机械臂轨迹，在保证组合体相对稳定且角速度较小的同时，有效抑制了组合体柔性部件的振动。文献[17]利用混沌粒子群算法，研究了基座姿态扰动最小时的机械臂轨迹规划问题，使机械臂轨迹平滑运动的同时减少了对卫星姿态的影响。为了尽快使抓捕后的非合作目标稳定，文献[18]研究了空间机器人最优消旋策略和协调控制方法，提出了一种同时使平台姿态和抓捕目标一起稳定的控制方法。以上学者在对机械臂轨迹规划的过程中，大都只考虑了对卫星平台的扰动，忽略了机械臂关节控制力矩的能量消耗问题。

针对上述方法的不足，本文分析了抓捕瞬态碰撞对机器人系统产生的影响，并提出了一种控制力矩能量消耗少、对卫星平台基座扰动小的镇定控制方法。首先，利用ADAMS软件建立并分析了空间机器人抓捕目标时的瞬态碰撞过程，为后续镇定控制策略的设计提供了相应的初始仿真参数；其次，采用四次多项式实现了机械臂关节空间轨迹的参数化，设定了基于控制力矩能量与基座扰动的加权目标函数，并利用差分进化算法(Differential evolution,DE)求解得到满足机械臂控制力矩能量消耗小、平台基座扰动少的机械臂关节空间轨迹；最后，基于空间七自由度漂浮机器人的数值仿真结果验证了所提出方法的有效性。

1 动力学建模

本文从两个方面研究了空间机器人的动力学建模问题。其一是利用ADAMS软件建立了七自由度空间机器人的瞬态碰撞模型，作为分析抓捕瞬态碰撞的仿真模型；其二是利用Kane方程建立了七自由度空间机器人抓捕目标后的组合体动力学模型，作为系统镇定控制器的设计基础。

1.1 空间机器人碰撞动力学建模

本文建立了七自由度刚体自由漂浮机器人动力学模型。机械臂各关节由球形铰链连接，机械臂末端附有抓手，充当抓捕工具。利用ADAMS软件的建模功能，并根据空间机器人参数，建立七自由度机械臂抓捕碰撞模型，如图1所示。该模型由机械臂、卫星平台和目标组成。在机械臂末端建立抓捕工具，并在目标上建立相应的抓手，如图2所示。

碰撞动力学的建模不仅涉及系统的动力学、弹性参数，还与碰撞物体的几何形状、相互嵌入量有关，很难有解析表达式。因此利用ADAMS软件中的等效弹簧阻尼函数对碰撞进行数值仿真[19]

(1)

式中：K表示模型的等效接触刚度，K的取值通常与接触体的材料刚度和几何形状选取有关；q表示两物体之间的穿透量；e表示非线性系数指数，当e≠1时表示非线性弹性，e=1表示线性弹性；Dmax表示碰撞物体的最大穿透量；Cmax表示接触时的最大阻尼；step为阶跃函数，其函数示意图如图3所示，利用三次多项式逼近阶梯函数，模拟等效弹簧阻尼函数的非线性阻尼模型，函数中q为自变量，其定义域为[0,Dmax]，函数值域为[0,Cmax]，当碰撞刚刚发生时，穿透量为0，阻尼为0，当穿透量为Dmax时阻尼为Cmax[20]。

图1 七自由度空间机器人抓捕碰撞模型Fig.1 Seven-DOF space robot impact model

图2 机械臂末端抓手模型Fig.2 End effector model of space robot

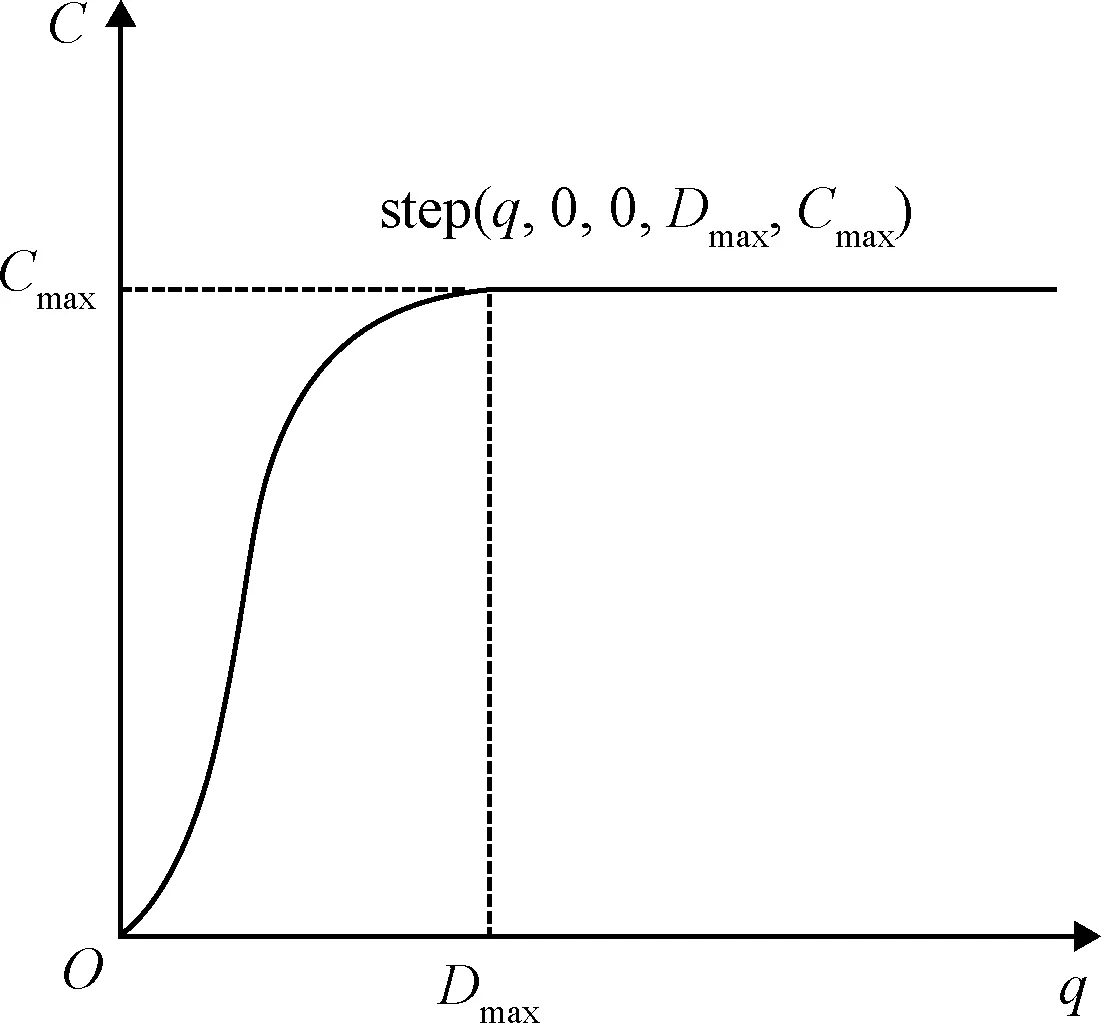
图3 非线性阻尼项特性曲线示意图Fig.3 Diagram of nonlinear damping characteristic curve

1.2 组合体动力学建模

为了描述抓捕目标后的组合体动力学特性，建立如图4所示的组合体动力学数学模型。其中B表示卫星平台，Li(i=1,…,7)表示机械臂的七个连杆，连杆之间由单自由度的旋转铰接关节ki(i=1,…,7)连接，b表示抓捕目标。

建立如图4所示的坐标系，在卫星平台质心处建立坐标系Ob表示卫星本体坐标系，Oi(i=1,…,7)表示连杆Li的本体坐标系，其坐标系原点位于旋转关节ki的铰接中心；Oiref表示关节ki的参考坐标系，其原点与Oi原点重合，且随铰接关节转动;r0表示平台质心在惯性系下的位置；ri(i=1,…,7)表示连杆质心在惯性系下的位置；pi(i=1,…,7)表示关节参考坐标系在惯性系下的位置。

图4 组合体系统模型Fig.4 Model of compound system

文献[21]中利用Kane方程[22]建立了具有几何约束的双臂空间机器人动力学模型，利用文献[21]中的动力学建模方法，本文建立了单臂七自由度抓捕目标后的空间机器人组合体刚体动力学模型

(2)

(3)

为了保证抓捕的成功，空间机器人系统在抓捕瞬态过程中对平台姿态不进行控制，最终组合体系统动力学可写为如下形式

(4)

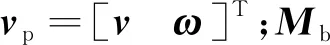
(5)

1.3 系统动量与角动量

当空间机器人系统稳定抓捕目标后，所形成的组合体系统不受外力作用，因此系统遵循动量守恒定律。文献[24]的方法建立系统动量、角动量守恒方程。文献[24]中描述的空间机器人系统具有l部机械臂，在l部机械臂中的第h个机械臂具有nk个自由度。系统动量和关于平台质心的角动量为

(6)

(7)

(8)

(9)

(10)

r0g=rg-r0

(11)

(12)

本文建立了单臂七自由度空间机器人模型，因此h=1。抓捕前目标与卫星平台之间存在相对运动，抓捕后目标将进一步带动机械臂各臂杆以及平台一起运动，因此抓捕后形成的卫星-机械臂-目标组合体系统具有初始动量与角动量。

由式(6)可以求解出平台速度表达式

(13)

将式(13)代入式(6)中得到

(14)

(15)

从以上的分析中可以得出：由于系统遵守动量守恒定律，因此由抓捕引起的系统初始动量、角动量大小无法改变，只能通过对关节角与关节角速度的优化来减少平台所受到的扰动。

2 抓捕瞬态仿真分析

碰撞初始时刻选取目标相对平台运动参数见表1，ADAMS碰撞参数见表2，机械臂D-H参数与空间机械臂各部分质量惯量见表3、4。其中仿真时间1s，仿真步长10-3s。采用GSTIFF积分器，SI2积分格式，积分误差为10-3。在碰撞仿真过程中，机械臂关节及平台不施加控制。碰撞前机械臂初始构型为[75,70,110,10,110,-96,94]T(°)，关节角速度与平台角速度均为零。

图5表示碰撞过程中机械臂关节角速度的变化情况。从图5可以看出第一次碰撞发生在0.007 s，末端抓手碰撞，造成关节角速度突变；碰撞发生后，由于没有采取镇定控制策略，所以在0.2 s时发生第二次碰撞且各关节开始随动，造成末端抓手受力、关节角速度以及平台状态的突变，因此需要在二次碰撞之前进行镇定控制。选取0.1 s时机械臂关节角速度[-0.19,0.54,0.01,0.02,-1.11,3.19,-2.05]T(°)/s作为后续镇定控制策略的初始仿真参数。

表1 碰撞初始时刻目标相对平台角速度、速度Table 1 Relative velocity and angular velocity between target and platform at initial time of impact

表2 碰撞参数Table 2 Parameters of collision

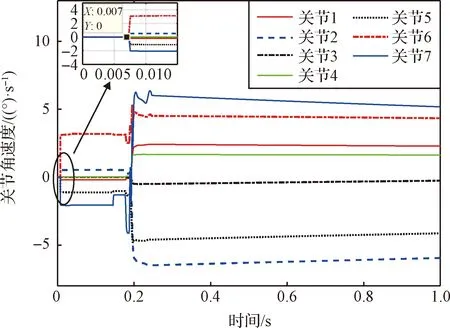
图5 碰撞过程关节角速度变化曲线Fig.5 The curve of joints angular velocity during impact

图6表示碰撞时平台角速度的变化曲线。从图中可以看出抓捕瞬态对卫星平台本体影响有限，在碰撞过程中平台总体保持稳定。第一次碰撞对平台造成的角速度突变小于10-4(°)/s量级；第二次碰撞对平台造成的角速度突变超过0.02(°)/s。

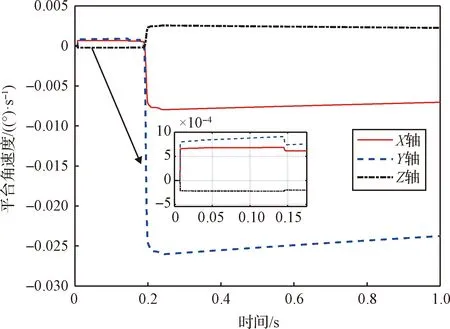
图6 碰撞过程平台角速度变化Fig.6 The curve of platform angular velocity during impact

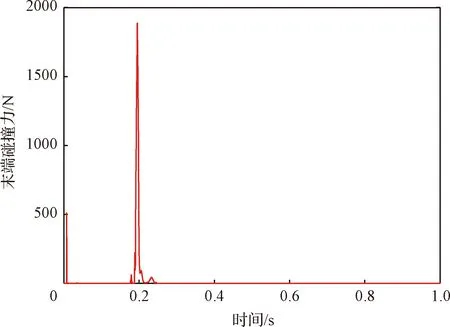
图7 末端碰撞力大小Fig.7 The magnitude force of end effector during impact

图8 末端碰撞力矩大小Fig.8 The magnitude torque of end effector during impact

图7、8分别表示碰撞时末端抓手所受碰撞力、力矩大小变化曲线。力矩的突变证明了碰撞的发生，碰撞力的两次突变对应系统状态的两次突变。

综合以上抓捕碰撞仿真结果，可以得出以下结论：

1) 末端抓手在抓捕过程中与目标发生碰撞，造成关节角速度的突变；在碰撞发生后，由于没有采取相应的镇定控制策略，机械臂各关节开始随动并发生第二次碰撞，造成抓手受力过大，关节与平台状态变化剧烈，因此需要在二次碰撞之前设计相应的随动控制策略进行镇定控制。

2) 抓捕冲击对卫星本体影响较小，卫星平台在抓捕瞬态保持稳定。

因此针对抓捕目标后的组合体系统，根据抓捕碰撞仿真分析结果，做出如下假设以辅助设计组合体镇定控制策略：

假设1.抓捕结束后，末端抓手与目标之间不产生晃动，抓手与目标之间为刚性连接，目标附着在末端抓手上随机械臂一起运动。

从碰撞仿真结果可以看出，碰撞过程时间很短，根据文献[25]中的分析，可用冲量定理描述抓捕碰撞对系统的冲击效应，假设碰撞在短时间Δt内完成，则末端抓手碰撞力在碰撞瞬间的冲量可等效为

(16)

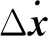
利用冲量原理对瞬态抓捕碰撞进行分析：系统受到的碰撞冲击与碰撞后系统速度变化的大小相关，碰撞冲击大则系统速度变化大，碰撞冲击小则速度变化小。由碰撞仿真分析结果可以得出，第一次瞬态碰撞对卫星本体基座影响较小，因此针对抓捕瞬态碰撞对系统产生的影响做出如下假设：

假设2.抓捕瞬态碰撞对空间机器人系统产生的冲击效应以机械臂关节角速度的形式体现。

3 基于差分进化算法的轨迹规划镇定控制

为了辅助设计机械臂镇定控制策略，基于假设1与假设2可以将镇定控制问题等效为：根据已知的初始状态和终止状态，求解一条机械臂运动轨迹，在满足一定约束条件的情况下，达到消除目标相对运动与镇定组合体系统的目的。本文将抓捕冲击产生的关节角速度看作轨迹设计的初始状态，将关节角速度、角加速度为零看作终止状态进行轨迹的优化设计。

3.1 关节空间轨迹参数化

在机械臂轨迹规划问题中，常采用多项式函数插值的方法对轨迹进行逼近。在本文中机械臂初始与终点状态的关节角、关节角速度已知，因此利用多项式设计关节轨迹如下

θi=a0i+a1it+a2it2+a3it3+a4it4

(17)

对式(17)求一阶导数与二阶导数，分别求得关节角速度和角加速度的表达式

(18)

(19)

式中：T,θTi分别表示轨迹规划时间与终点关节角构型。

从式(19)中可以看出，设计的四次插值多项式轨迹由阻尼时间T与终点关节角θTi决定。针对这一特点，本文通过对T,θTi的优化，求解得到满足相关约束条件的运动轨迹。

为了实现组合体镇定过程中控制力矩能量消耗小、对平台扰动少的目的，联合式(5)与式(15)，选取控制力矩能量消耗与卫星平台角速度累计变化作为评价指标：

(20)

除此之外，在设计机械臂轨迹的过程中，各关节还应满足如下约束条件

(21)

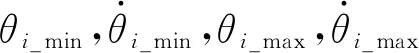
3.2 差分进化算法

差分进化算法由Storn等在文献[26]中提出，该方法利用群体进化理论通过种群内个体间的竞争与全局搜索来实现对问题的优化计算。针对式(22)所示的优化问题[27]，DE算法利用变异、交叉、选择操作实现问题的优化求解。

(22)

其中:z(x),h(x)表示与优化变量x有关的函数约束条件。

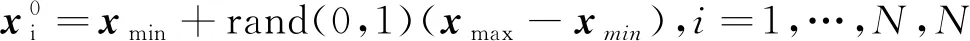
配电自动化的核心是馈线自动化(Feeder Automation,FA),即配电线路自动化,在线路开关上添加馈线自动化终端设备,以实现远程监控。馈线自动化终端可分为具有遥测、遥信、遥控功能的“三遥”配电终端;具有遥测、遥信功能的“二遥”配电终端;仅有遥测功能的“一遥”配电终端[3]。不同地区的终端配置可根据各自的可靠性要求进行优化选择。通过对线路中开关的控制可以优化网络结构和提高供电可靠性[4],而馈线自动化终端优化配置也必须要统筹考虑投资与可靠性的关系,从而达到配电网建设运行的经济性与可靠性的目的。

(23)

式中：i,r1,r2,r3=1,2,…,N，且r1,r2,r3为随机选中的互不相同的数；F为缩放比例因子，取值范围在[0,1]。

(24)

式中：j=1,…,D表示种群中元素的序列数；jrand表示[1,D]之间的随机整数；rand(j)表示[0,1]之间均匀分布的随机数；C为变异常数因子。

变异因子C越大则越有利于提高算法的局部搜索能力，且收敛速率快；C越小则越有利于保持种群的多样性，且全局搜索能力强。

为了让优化变量都处在规定的范围内，在标准差分进化算法中加入边界条件限制：

(25)

(26)

根据以上步骤，本文利用差分进化算法对式(20),(21)所示的问题进行优化计算。根据式(19)定义优化变量x

(27)

式中：Δθi(i=1,…,7)表示机械臂终止状态相对初始状态的关节角偏移量，θTi=θ0i+Δθi；T表示轨迹规划时间。

其中优化变量中的约束条件为：

(28)

综合任务需求考虑，本文定义适应度函数如下：

J=Jv+Jp

(29)

其中，Jv表示评价指标

(30)

评价指标中包括了机械臂关节控制力矩的能量消耗以及对平台的累计扰动。除此之外，根据约束条件，设置惩罚函数Jp如下所示

(31)

(32)

(33)

最终，利用差分进化算法对轨迹进行优化的流程如下：

1)设置种群维数D与种群数量N，并选取优化变量x。

5)设定种群的上限与下限，保证种群在设定的范围内进行搜索。

6)将以上五个步骤产生的种群代入适应度函数，并利用贪婪法则对种群进行筛选。

7)重复2)～6)步骤直到最大进化代数G，最终得到适应度函数值以及优化变量x。

阻尼轨迹优化流程如图9所示，差分进化算法计算流程如图10所示。

图9 阻尼轨迹优化流程框图Fig.9 Flow diagram of damping trajectory

图10 差分进化算法流程图Fig. 10 Flow chart of DE algorithm

3.3 机械臂控制器设计

为了跟踪优化后的轨迹，根据式(5)设计机械臂关节控制器：

(34)

(35)

选取合适的正定矩阵Kp,Kd，证明控制器的稳定性，构造李雅普诺夫方程如下

(36)

根据李雅普诺夫稳定性原理，对李雅普诺夫函数求导：

(37)

又因为V≥0，所以根据李雅普诺夫稳定性原理可证明系统全局渐近稳定，因此设计的控制器可以实现对期望轨迹的稳定跟踪。

4 仿真校验

本文利用图4所示的七自由度空间机器人组合体模型对所提出的控制策略进行仿真校验。组合体机械臂D-H参数见表3。

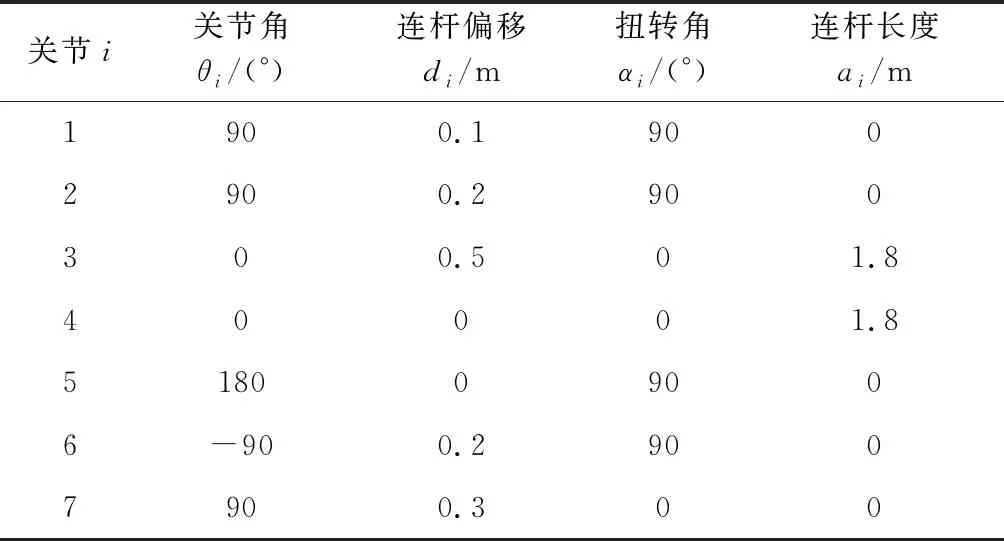
表3 机械臂D-H参数Table 3 D-H parameter of manipulator

4.1 轨迹优化结果

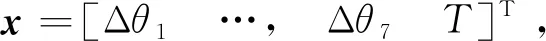
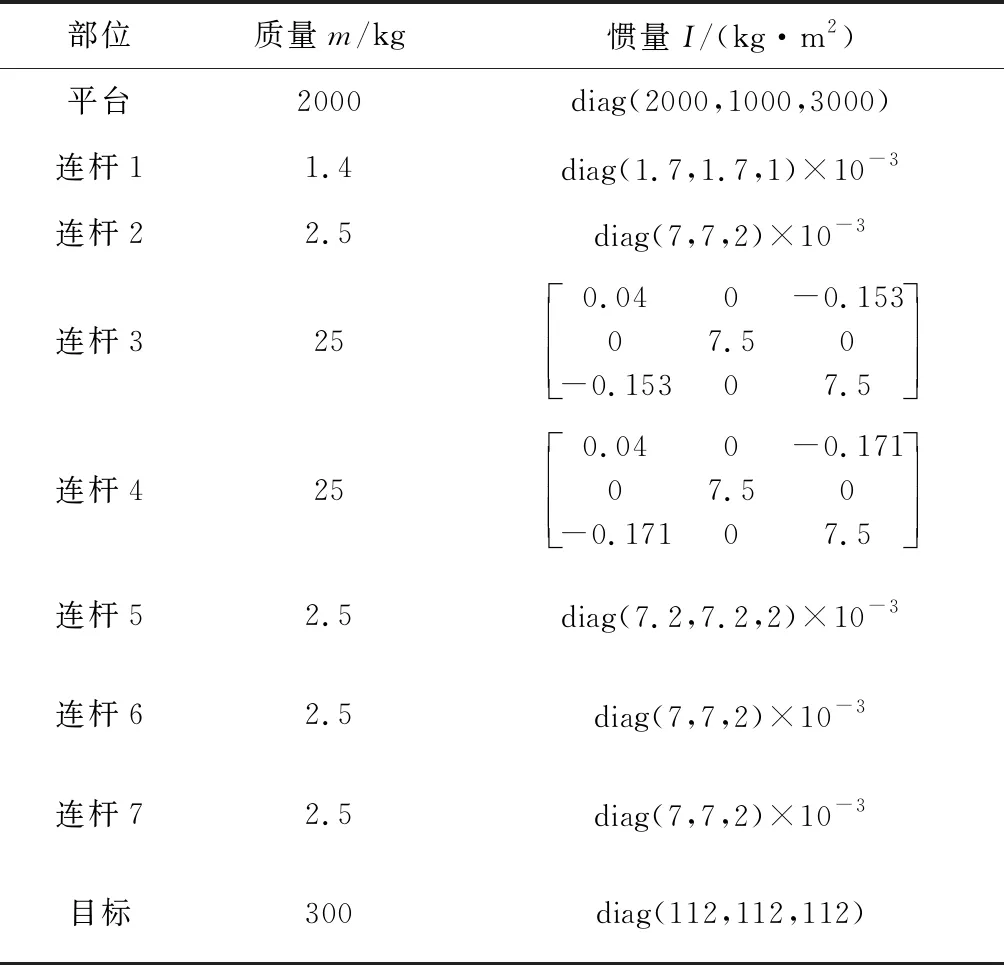
表4 系统质量惯量Table 4 Mass and inertia of system

(38)

将给定的关节角速度和机械臂构型作为初始仿真参数，并利用DE算法求解关节角偏移量和阻尼时间。

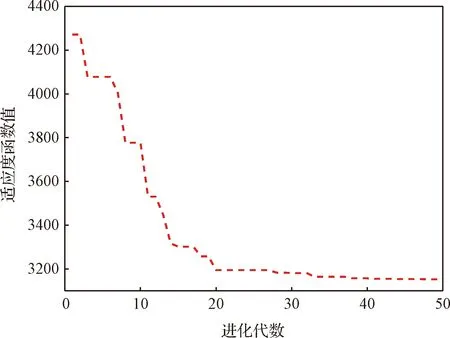
图11 适应度函数收敛曲线Fig.11 The convergence curve of fitness function

图11表示适应度函数值随进化代数的收敛曲线。最终得到适应度函数优化值J=3149.7，阻尼时间T=123.44 s，关节角相对初始构型偏移量Δθ=[31.96,31.54,21.64,-4.12,39.99,-15.05,-27.49]T(°)。

结合式(27)将Δθ、T代入式(19)得到轨迹曲线，最后利用式(34)的控制器对轨迹进行跟踪，得到关节角、关节角速度、平台角速度和关节控制力矩曲线如图12～15所示。从图12关节角速度曲线可以看到，利用文中提出的镇定控制方法使关节角速度最终收敛到零，消除了目标的相对运动，达到了维持被捕获目标与卫星本体之间相对稳定的目的。特别注意图14中机械臂控制力矩的变化，由于卫星平台为自由漂浮状态，当卫星平台运动时关节仍需保持对期望轨迹的跟踪，因此控制力矩始终不为零。

图12 关节角速度曲线Fig.12 The curve of joints angular velocity

图13 关节角轨迹Fig.13 The trajectory of joint angles

图14 关节控制力矩Fig.14 The control torques of joints

图15 平台角速度Fig.15 The angular velocity of platform

4.2 优化与未优化结果的对比

为了验证本文所提出算法的有效性与优越性，将其与未进行优化的轨迹结果进行对比分析。

另给定区别于本文优化结果的四次多项式轨迹作为期望轨迹进行跟踪。在相同仿真时间下利用相同控制器，即式(34)对轨迹进行跟踪，并设定如下指标进行对比：

机械臂运动对平台的累计扰动：

(39)

机械臂关节控制力矩能量消耗：

(40)

平台角速度扰动范数：

(41)

由图16和图18平台扰动对比曲线可以看到，优化后的轨迹在阻尼镇定过程中对平台的扰动更小，达到了对平台扰动少的目的；由图17关节控制力矩能量消耗对比曲线可以看出，优化后的控制能量消耗更少。

图16 平台累计扰动Fig.16 Accumulation disturbance of platform

图17 关节控制力矩能量消耗Fig.17 The energy cost of control torque

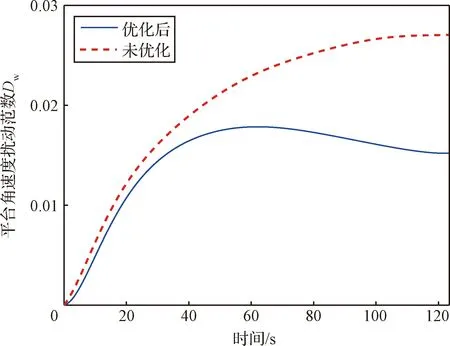
图18 平台角速度扰动范数Fig.18 The norm of platform angular velocity

根据以上仿真对比曲线可以得出，本文提出的镇定控制策略对抓捕目标后的空间机器人系统具有良好的阻尼镇定效果，达到了控制力矩能量消耗小、对平台基座扰动少的控制目标。

5 结 论

本文针对空间机器人抓捕目标后对系统产生的冲击问题，利用ADAMS软件建立并分析了抓捕瞬态冲击对空间机器人系统产生的影响，为镇定控制策略的设计提供了初始仿真参数。采用四次多项式插值的方法实现了机械臂关节空间轨迹的参数化,利用差分进化算法求解得到满足控制力矩能量消耗小、对平台基座扰动少的轨迹。与未优化的仿真结果相比，本文提出的镇定控制策略与轨迹规划方法在减少控制力矩能量消耗和对平台扰动的同时，实现了对抓捕目标后组合体系统的阻尼镇定，减小了碰撞冲击对系统产生的影响，维持了被捕获目标与卫星本体之间的相对稳定。