磁场中荷电粒子动量分量间不对易性和角动量的一个新关系

陈俊风，谢蔚鑫，王 鑫，刘全慧

（湖南大学 物理与微电子科学学院 理论物理研究所，湖南 长沙 410082）

磁性的一个本性是旋转性，但这一点并不容易理解.例如，麦克斯韦利用涡管构造了磁场的力学模型［1］，很多名家解读过麦克斯韦的涡管模型［1-3］.较为容易理解的事实是，旋转参考系中的很多物理现象，可以类比于磁场并借用磁场的理论进行处理［4，5］.关于旋转运动的力学，近十年来有一个独立的研究进展.对于约束在超球面上的运动粒子，粒子动量不同分量间的泊松括号或者对易关系不为零，而是正比于角动量的一个分量［参见下文中的式（9）］.本文把粒子动量不同分量间的泊松括号或对易关系都称为不对易性，而且磁场为稳恒场，但不要求空间分布均匀.

于是，一方面，粒子局限在球面上的自由运动，旋转是其本性；另一方面，“磁性本质上是旋转性”（英文原文:magnetism was essentially rotational in nature.这一观点的历史源头及其在认识磁性中的意义，参见文献［1］及其参考文献）.由于旋转性是它们二者的一个共性，应该有类似的描述［6，7］.注意到，磁场中荷电粒子动量不同分量间不对易，球面上运动粒子动量不同分量间也不对易［8，9］，不过这两个不对易性相差很大.本文的主要结果是，二者可以统一到一个表达式里.

其中 q 为粒子的电荷，pi和 Bi（i＝ 1，2，3）为粒子和磁场的三个空间分量.在量子力学中通过将对应关系转化为量子力学对易关系或者量子条件［9］.如果式等号的右边可以改写为依赖于角动量的形式，则可以从另外一个角度给出“磁性本质上是旋转性”的明显形式.

第1节中，将证明式等号的右边可以改写为依赖于角动量的形式，但是这个角动量是瞬时角动量.第2节中，将讨论这个角动量是否满足角动量的量子力学定义.第3节是结论.

1 磁场中荷电粒子动量分量间不对易性

考虑到荷电粒子在磁场中受到的洛伦兹力

洛伦兹力公式认为力学动量p的大小不会改变，仅仅改变方向.把洛伦兹力式（2）和拉莫尔旋进动公式比较，立即发现粒子的角速度为

角速度的大小也被称为拉莫尔频率.

注意到粒子角速度是一个和参考系无关的性质，但是速度是一个和参考系有关的量.这个参考系中，磁场不含时间.也就是说，粒子速度v必须相对于一个固定参考系，参考图1.由于磁场在空间的分布和时间无关，粒子的角速度ω也将是空间点的函数.粒子每时刻在空间的不同点，也就是每个瞬时的角速度互不相同.因此，每个时刻粒子都在一个独自的瞬时平面和瞬时圆周（实际轨迹可能只是圆周的一小段）上.设瞬时圆周的半径为 ρ＝r-R，则如下关

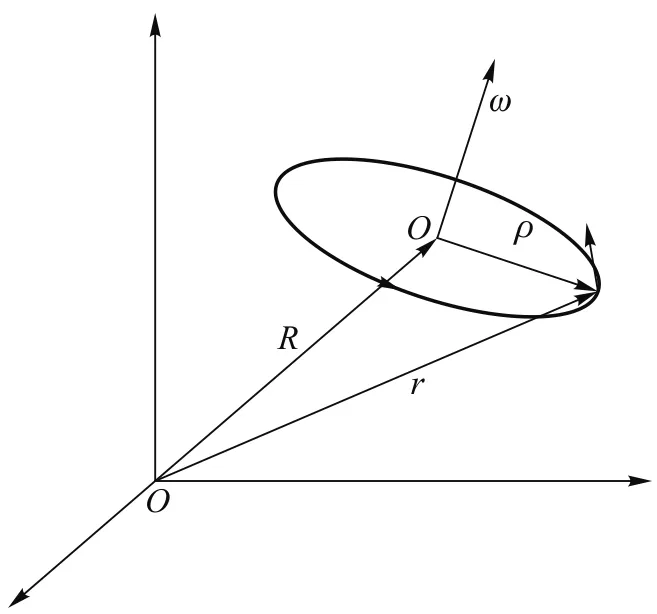
图1 固定参考系中的瞬时平面和瞬时圆周

从洛伦兹力公式也可以解出速度v（或者由初始条件决定），这样从式（6）就可以解出ρ.

把这个结果代入式（1），即得

其中Lk为粒子角动量的三个分量，ρ为粒子瞬时转动平面中的瞬时半径.这和二维球面上运动粒子动量不同分量间的经典括号的关系完全一样［6，7］，不过，在球面上，泊松括号必须换成狄拉克括号.

2 力学角动量的经典和量子力学

在经典力学中，粒子的力学角动量可以针对空间中的任意参考点来定义:

这个定义，不仅仅适用于力学角动量，也适用于正则角动量.

在量子力学中，角动量必须满足对易关系［Li，Lj］＝iℏϵijkLk，也就是在经典力学中必须满足经典对易关系［Li，Lj］＝ϵijkLk.在经典和量子力学中，这个关系和定义式（10）是否相容，需要细究.

首先，计算如下泊松括号［Li，Lj］，结果是

把 r＝ρ+R 代入，立即发现，当且仅当 r＝ρ，［Li，Lj］＝ϵijkLk.即经典力学中，仅仅对转动瞬心定义的力学角动量是合适的.

第二，经典力学关系中式（9）中暗含了经典力学运动方程的解式（5）或者式（8）.一般而言，这些关系在量子力学中，只在期待值意义上才成立.

一个细致的问题如下.在量子力学中，如果对瞬心力学角动量，首先必须定义瞬心.问题是，对于稳恒均匀的磁场中的荷电粒子，转动瞬心的坐标的不同分量不对易［9］.因此，量子力学中是否能定义力学角动量，不容易有个清晰的结论.同时很容易发现，量子力学中，定义角动量的一个恰当方式是定义正则角动量.因此，在量子力学中，正确的步骤是先定义正则角动量，然后再看其他角动量的存在性及其意义.

3 结论

磁场中荷电粒子动量分量间具有不对易性是一个熟知的事实，磁性本质上是旋转性也是一个熟知的事实.本文认为，把磁场中荷电粒子动量分量间具有不对易性和角动量联系起来，可以给磁性本质上是旋转性这个定性事实一个定量的表达式.这个结果，在经典力学中总能成立，但在量子力学中，仅仅在一些波包上求期待值的时候，才能成立.