考虑数据缺失的电力系统暂态稳定自适应集成评估方法

谭本东，杨 军，刘 源，刘雯静，周 挺，孙元章

（1. 武汉大学电气与自动化学院,湖北省武汉市 430072；2. 国网江西省电力有限公司建设分公司,江西省南昌市 330029）

0 引言

暂态稳定性指的是电力系统在遭受大干扰之后过渡到稳定状态的能力［1］。大电网之间的互联、多种大规模可再生能源的接入以及电力市场的推进使得电力系统调度运行以及安全稳定控制面临严峻挑战,容易引发大停电及连锁故障等电网事故［2-3］。因此,快速、准确地评估暂态稳定状态对于电网安全稳定运行具有重大意义。

随着同步测量技术的发展［4-5］和电力系统仿真技术的进步,实际电网数据和仿真数据为数据驱动型方法提供了足够的数据基础。此外,广域测量系统 中 同 步 相 量 测 量 单 元（synchrophasor measurement unit,PMU）实时高速采集数据的能力也为数据驱动的暂态稳定评估方法提供了发展契机。特别是近几年人工智能技术研究的持续突破,利用机器学习来研究暂态稳定的方式展现出了巨大的潜力。一般而言,通过历史量测数据离线训练机器学习方法即可建立量测数据与稳定状态之间的函数映射关系,一旦从PMU 中在线获得测量值,即可判断出电力系统的暂态稳定状态［6-8］。因此,利用机器学习进行暂态稳定评估可以做到实时判断并为后续可能的紧急控制动作留下足够的时间。由于本文重点不在紧急控制,因此不对如何将暂态稳定评估结果用于紧急控制做详细讨论,基于数据驱动的暂态稳定紧急控制相关内容可参见文献［9-10］。

目前机器学习方法在实时暂态稳定评估研究工作中取得了一定的成果,支持向量机［11-12］、决策树［13-14］、神经网络［15-16］等方法均在这个领域成功应用,它们根据故障切除后的关键特征和稳定状态之间的映射关系来实施暂态稳定评估,结果表明这些方法具有很高的准确性、快速性并适用于大规模电力系统。但是,电力系统可能发生通信延迟及PMU失效,造成基于机器学习的暂态稳定评估模型数据特征输入缺失,在这种情况下其评估性能会极度恶化。为了解决这个问题,主要有2 种研究思路。第1种是利用预测方法对缺失的数据进行修复［17］,但是这种策略计算量较大,无法满足实时评估的需求。第2 种是根据数据特征之间的相关关系来降低数据缺失的影响。文献［18］利用决策树的特征分裂特性求取替代缺失特征的分支,但是其受到数据缺失的影响依然严重；文献［19-21］基于满足电网可观性的最少数量特征子集构造集成模型来提高模型对数据缺失的鲁棒性,然而它们需要满足全网特征的可观性且没有考虑PMU 在重要性上的不同,最终在准确率、计算量和鲁棒性上均有不足；文献［22］利用对抗生成神经网络来对缺失的数据进行填充,但是这类方法易受到噪声的干扰且需要大量的算力来训练此类模型。

针对上述研究工作的不足,本文提出了一种考虑数据缺失的电力系统暂态稳定自适应集成评估方法。首先,分析了电网PMU 观测性的基本概念,基于此提出了考虑PMU 可观测特征重要性的PMU子集搜索算法,并通过保证全网节点可观性大大减少PMU 子集的数量,从而降低后续训练模型的计算量。然后,根据PMU 子集集合提出了一种应对PMU 失效的自适应集成评估方式。最后,在新英格兰10 机39 节点电力系统上对本文所提出的集成评估方法进行仿真验证。

1 满足电网节点可观性的PMU 子集集合

1.1 电网PMU 观测性

PMU 是一种能够同步测量电网相量的设备,假设某一母线安装了PMU,那么与其相连的母线及线路均可观测,PMU 可观性的具体规则可见文献［23］。为了获得对全网的可观性,需要确定最优的一组PMU 安装位置来实现这一目标。此外,当电力系统中存在零注入节点时,可以减少配置PMU的数量。为简化分析,本文只考虑存在零注入节点的情况,下面以3 机9 节点电力系统为例说明PMU可观性的概念,该电力系统结构如附录A 图A1所示。

附录A 图A1 中只需要在4 号和7 号母线上安装PMU 即可对全网观测。具体而言,安装在4 号母线上的PMU 可以实现对红色虚线框内的1、4、5、9 号母线直接观测；安装在7 号母线上的PMU 可以实现对紫色虚线内的6、7、8 号母线直接观测。2 号和3 号母线则可以通过基尔霍夫定律实现可观性。

因此,在保证全网节点可观性的PMU 配置下,基于机器学习的暂态稳定评估方法只要获得了全网的数据,就能快速、准确地对故障后电力系统的稳定状态进行判断。但是,当某些PMU 失效或者通信故障发生之后,这类方法评估结果的准确率会急剧下降而变得非常不可靠。所以如何根据PMU 配置的特性来降低数据缺失的影响是本文研究的主要内容。

1.2 特征重要性计算

在电力系统遭受干扰后的动态过程中,一般表现为某几台发电机失步造成暂态失稳的主导模式。而电力系统运行状态定义为一组状态变量,例如电压幅值、电压相角等,因此电力系统存在一些相对重要的特征（电压、电流、功率等）来展现出暂态特性。那么在电网中安装的每个PMU 由于其可观测范围不一样,其在重要性上也是有区别的。为了定量计算电网中每个变量的特征重要性,本节引入经典的Relief-F 算法［24］来进行求解。对于特定的PMU,其重要性计算公式为：

式中：I为特征重要性之和；Wai为特征ai的特征重要性；ψ为该PMU 可观测的特征集合。

1.3 基于重要性的PMU 子集搜索算法

一旦发生PMU 失效,基于机器学习的暂态稳定评估方法就有可能失去其有效性,因此本文采取分而治之的思路来降低数据缺失的影响。具体而言,根据不同PMU 的重要性及其观测范围来寻找一组保证全网节点可观性的PMU 子集集合,在这个集合之下分别对子集中所包含PMU 观测到的特征建立机器学习模型。最后利用加权集成的方式来实现模型融合,当若干个PMU 失效造成数据缺失后,剩下不被数据缺失影响的PMU 子集对应的模型依然能进行加权集成并能够给出可靠的评估结果。

按照上述思路,对于安装有N个PMU 的电力系统,可能的PMU 子集有2N−1 个,如果全部利用则需要训练2N−1 个模型,这会造成巨大的训练量。文献［20］通过找到满足全网特征（电压、电流）可观性的最简PMU 子集集合来实现降低数据缺失的影响。实际上只要保证节点（电压）可观性的最简PMU 子集集合,则全网电流可利用基尔霍夫定律获得（文中假设可以通过机器学习获得这一隐含关系）,那么可以在不影响模型性能的情况下大大降低计算量。值得注意的是,这里描述的全网可观性（特征可观性）是指所有PMU 子集可观测的特征范围的并集,文献［19-20］在搜索PMU 子集过程中并未利用基尔霍夫定律对PMU 子集之间的关系进行分析,因此在PMU 子集搜索目标为全网节点电压可观而非全网节点电压及全网电流同时可观时,需要构造的子集数量较少。

假设各机器学习模型对应的PMU 子集之间的交集为空集,那么将无法保证全网的节点可观性,这是因为PMU 在布局的时候利用了零注入节点和基尔霍夫定律的特点来减少PMU 数量,也就是说多个PMU 需要一同配合才能实现全网节点的可观性；又假设各个机器学习模型对应的PMU 子集相同,此时模型受到PMU 失效影响的可能性最大。因此,需要平衡全网可观性和PMU 失效影响的可能性。此外,PMU 的重要性在PMU 子集搜索过程中也是需要考虑的一个重要因素,因此本文提出了基于特征重要性的PMU 子集搜索算法,从数量最少的PMU 子集开始搜索,找到相同数量PMU 的子集中特征重要性最大的,直到达到全网节点可观性为止。其中,从数量最少的PMU 子集开始搜索是因为PMU 数量越少的子集其发生失效的概率越低,具体过程如附录A 图A2 所示,其中f(⋅)为根据1.1 节中PMU 观测性规则返回PMU 子集观测节点集合的函数。当确定电网拓扑参数及PMU 安装位置后,首先初始化PMU 子集集合Ω=∅,考虑1 个PMU 的可能子集情况,对所有PMU 子集按照PMU重要性从大到小进行排序分析；如果该PMU 子集能够增加新的可观测节点,那么其将被添加到集合Ω中。以此类推,逐渐增加包含PMU 数量的可能组合子集,直至全网的节点可观测。

2 暂态稳定自适应集成评估模型

2.1 支持向量机的基本原理

支持向量机是一种泛化性表现良好的二分类模型,目前在电力系统暂态稳定评估中取得了广泛应用［11-12,25］。其学习目标是在特征空间中找到一个分离超平面,能够将不同稳定状态的实例加以区分。假设给定一个特征空间的电力系统暂态稳定训练数据集T为：

式中：xi为第i个样本的特征向量；yi为第i个样本的标签,yi∈{−1,1},当yi=−1 时表示暂态稳定,当yi=1 时表示暂态失稳；i=1,2,…,L,其中L为数据集样本的数量。

为了获得最优分离超平面,支持向量机可以归结为下述优化模型。

式中：λ为惩罚参数；ξi为松弛变量；w为分离超平面法向量；φ(⋅)为核函数；b为超平面的截距。

为了对支持向量机进行自适应集成,需要对其输出进行概率化处理［25］,即

式中：ŷi为第i个样本的预测类别；P(ŷi)为预测类别为ŷi的概率；g(xi)=wTφ(xi)；sgn(⋅)为符号函数。

2.2 离线训练

基于机器学习的暂态稳定评估本质上是一种有监督学习,因此需要将数据集分为训练集、验证集以及测试集。综合前人的研究工作［7,26］,本文采用故障切除后第1 个周期的电压幅值、电压相角、线路有功功率、线路无功功率、发电机有功功率、发电机无功功率、负荷有功功率及负荷无功功率作为模型输入特征。暂态稳定状态η为模型的输出,可以定义为［27］：

式中：δmax为时域仿真结束后任意2 个发电机功角差的最大绝对值；η≥0 时样本被判定为暂态稳定,η＜0 时样本被判定为暂态失稳。

假设在1.3 节中搜索到M个PMU 子集,离线训练方式可以分为以下2 个步骤。

1）根据每个PMU 子集能够观测到的特征范围将训练集分割成M个训练子集,分别用来训练M个支持向量机。

2）若只采用单分类器对电网暂态稳定进行评估,任何一个PMU 失效都会造成整个模型的失效,因此本文采用多分类器集成的方法来进行暂态稳定评估,那么任何一个分类器失效都可以利用剩余分类器进行集成评估,而且理论上集成模型泛化能力优于单个分类器模型的泛化能力。为了实现对M个支持向量机进行加权集成,采用和分割训练集相同的方式来分割验证集,利用其来求取每个支持向量机的权重,可以定义优化模型进行求解,如式（7）所示。

式中：i=1,2,…,D,其中D为验证集的样本数目；ŷij为验证集中第i个样本根据第j个PMU 子集分割出数据的暂态稳定预测类别；ti为集成概率；αj为第j个支持向量机模型的权重；y͂i为验证集中第i个样本的集成评估结果。

式（7）中第1 个约束表示对M个支持向量机进行加权集成,由于支持向量机的概率输出区间为[0,1],当集成概率输出为0.5 时,表示该样本到最优分离超平面的距离为0,因此0.5 可以作为式（7）中第3 个约束的稳定状态概率阈值。

2.3 在线自适应集成评估

基于机器学习的暂态稳定评估方法严重依赖于测量数据的实时性及完整性,但是在实际应用中,由于通信延迟及PMU 失效均可能造成数据缺失。为了在任意可能发生数据缺失的情况下保证模型的准确性,本文提出了一种在线自适应融合集成暂态稳定评估方式,模型的整体框架如图1 所示,具体如下。

图1 所提模型整体框架Fig.1 Overall framework of proposed model

1）当某些PMU 子集受到数据缺失影响时,剩余不受数据缺失影响的PMU 子集集合定义为Φ,则对剩余可用模型进行自适应加权集成的输出为：

式中：i=1,2,…,T。

3 算例分析

3.1 数据集生成

本节采用如附录A 图A3 所示的新英格兰10 机39 节点电力系统来构造数据集并验证本文提出的模型的有效性。文献［28］给出的保证全网可观性的最少数量PMU 的4 种布局方案如表1 所示,图A3中红色圆点表示方案1 中PMU 的安装位置。

表1 不同PMU 布局方案Table 1 Layout schemes of different PMUs

利用电力系统分析软件PSS/E 编写暂态稳定批处理程序,生成大量暂态数据集来训练本文提出的模型。考虑不同的故障方式及运行水平,最终生成了5 775 个样本,具体时域仿真参数设置如下。

1）考虑11 种不同的负荷水平（基准负荷水平的75%、80%、85%、90%、95%、100%、105%、110%、115%、120%、125%）,同时,发电机的输出功率也按照相同的比例调节。

2）每种运行水平下,分别在每个母线及线路的4 个位置（与首端的距离为线路总长的20%、40%、60%及80%）施加三相短路接地故障。

3）对于每个特定的瞬时故障,故障持续时间设置为0.1 s、0.3 s 或者0.5 s。

4）每次时域仿真总时间为10 s,仿真步长为0.01 s。

5）为了防止模型学习过拟合,所有数据集样本按照3∶1∶1 的比例分割成训练集、验证集及测试集,其中训练集用来训练每个支持向量机,验证集用来对所有支持向量机加权融合集成,而测试集则是对本文提出的模型进行评估。

3.2 特征重要性分布

根据Relief-F 算法的特性可知,重要性越高的特征表明其区分不同类别样本的能力越强。通过计算可以得到所有特征的重要性,见附录A 图A4,所有特征重要性按照降序排列,可以看到极少数特征的重要性是负值,绝大部分特征对于暂态稳定评估都具有正面影响。在新英格兰10 机39 节点电力系统中,PMU 配置下所有28−1=255 种可能的PMU子集对应可观测的特征的重要性之和的分布见图A5,可以看出不同PMU 子集的重要性是不一致的,PMU 子集的重要性和包含的PMU 数量呈正相关。但是为了降低模型训练的复杂度,本文只考虑保证全网节点可观测情况下重要性最高的最简PMU 子集集合。

3.3 不同PMU 布局方案下的模型性能分析

通过在新英格兰10 机39 节点电力系统上应用基于重要性的PMU 子集搜索算法,得到不同PMU布局方案下的PMU 子集数量对比,如表2 所示。可以看出,和文献［20］相比,本文提出的方法在PMU子集数量上最多可以降低26.32%,这在实际应用中减少的计算量是非常可观的。这是因为文献［20］要保证的是全网特征量的可观性,而本文提出的PMU 子集搜索方法则只需要保证全网节点可观性,最后利用集成学习获取特征之间的相关性。

表2 不同方法的PMU 子集数量对比Table 2 Comparison of the number of PMU subsets with different methods

本文提出的自适应集成评估方法在不同布局方案下平均准确率随着PMU 失效数量的变化趋势如图2 所示。

图2 不同PMU 布局方案下平均准确率变化Fig.2 Variation of average accuracy with different layout schemes of PMU

由图2 可以看出PMU 失效数越多,平均准确率越低。由于应对数据缺失的自适应集成机制的作用,只要存在未失效的PMU,平均准确率就能够保持在98%以上,说明提出的方法对PMU 失效具有较强的鲁棒性。此外,不同PMU 布局方案下模型的暂态稳定评估表现,也可以为PMU 布局设计提供参考。

3.4 模型性能对比分析

进一步验证本文提出的基于PMU 子集集合搜索结果的暂态稳定自适应集成评估方法在应对数据缺失上的有效性,目前应用于处理电力系统暂态稳定评估数据缺失的方法有：数据平均修复（mean imputation,MI）［29］、基 于 替 代 分 支 的 决 策 树（decision tree with surrogate split,DTSS）［18］、基于替代分支的随机森林（random forest with surrogate split,RFSS）［30］、基于前馈神经网络的集成投票（用Ensemble RVFL 表示）［20］,在文献［20］中已经证明Ensemble RVFL 方法优于上述的其他方法,因此用Ensemble RVFL 方法与本文提出的方法进行对比。以PMU 布局方案1 来进行说明。以上所有模型参数均通过网格搜索确定,实现了自身评估结果的最优化。

本文提出的PMU 子集方法搜索得到的PMU安装母线编号子集的结果为：{3},{8},{10},{16},{20},{23},{25},{29},{3,16},{3,10},{16,20},{3,8,10},{3,8,25},其重要性如附录A 图A6 所示。图A6 中A 区表示包含1 个PMU 的子集重要性,B区表示包含2 个PMU 的子集重要性,C 区表示包含3 个PMU 的子集重要性。可以看到,在每个区中每个子集的特征重要性呈下降趋势,表明了本文提出的PMU 子集搜索算法优先选择特征重要性高的PMU 子集的特点。

定义总体准确率E为：

式中：a为PMU 的失效率。

图3 展示了在不同PMU 失效数量下不同方法的平均准确率。

图3 不同PMU 失效数量对平均准确率的影响Fig.3 Effect of different numbers of PMU failure on average accuracy

由图3 可以看出,本文所提出的方法在任何PMU 失效情况下的平均准确率都是最高的。结果表明,本文提出的方法虽然只考虑了全网节点可观性而使用更少的PMU 子集,但是因为采用的基分类器为支持向量机以及消除了PMU 子集的冗余性而在性能上优于Ensemble RVFL 方法。

图4 呈现了PMU 失效率与总体正确率之间的关系,表明PMU 失效率对本文提出的方法及Ensemble RVFL 方法影响甚微。一般而言,单个PMU 的失效率不会超过2%［18］,因此当PMU 失效率设置为2%时,可视为在实际中可能发生的最严重情况。本文仿真计算发现,当PMU 失效率设置为2%时,本文提出方法对暂态稳定评估的准确率为99.13%,优于文献［20］中Ensemble RVFL 方法的准确率（98.34%）。

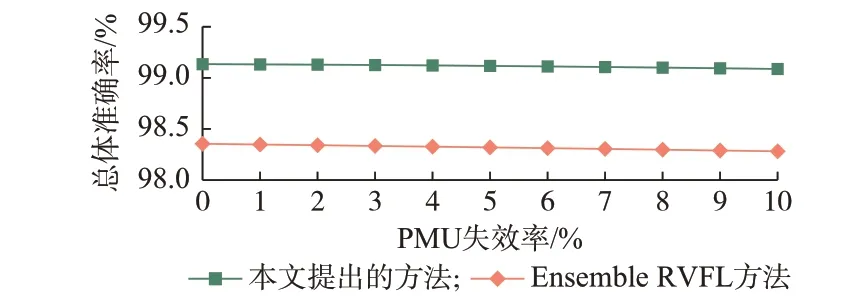
图4 不同PMU 失效率对总体准确率的影响Fig.4 Effect of different PMU failure rates onoverall accuracy

3.5 广域噪声对模型性能的影响分析

在之前的分析中,假设所有的系统量测都是精确的,但是实际广域测量系统不可避免地存在噪声。因此,本节将分析广域噪声对不同模型性能的影响。根据文献［18］中对PMU 所制定的标准,PMU 量测向量误差应小于1%,具体表达式为：

式中：X͂∠θ͂为从广域测量系统获取的量测数据相量；X∠θ为广域测量系统量测数据向量减去噪声之后的真实值。

图5 和图6 分别展示了在广域噪声影响下,不同方法平均准确率和PMU 失效数量、总体准确率和PMU 失效率的关系,其表现出的基本规律和没有噪声影响时一致。

图5 噪声影响下不同PMU 失效数量对平均准确率的影响Fig.5 Effect of different numbers of PMU failure with noise on average accuracy

图6 噪声影响下不同PMU 失效率对总体准确率的影响Fig.6 Effect of different PMU failure rates with noise on overall accuracy

从图7 可知,广域噪声越大,模型暂态稳定评估总体准确率越小,但本文提出的方法是一直优于Ensemble RVFL 方法。本文提出的方法在所有方法中所取得的性能是最好的,总体准确率在2%的PMU 失 效 率 下 为98.65%,优 于 文 献［20］中Ensemble RVFL 方法的97.70%。这是因为采取的基分类器支持向量机采用了松弛变量,对可能存在的异常点进行“容忍”,提高了对噪声的鲁棒性。

图7 广域噪声对模型总体准确率的影响Fig.7 Effect of model with wide-area noise on overall accuracy

4 结语

针对PMU 失效情况下造成的数据缺失问题,本文提出了一种电力系统暂态稳定自适应集成评估方法,能够有效降低数据缺失带来的影响。在新英格兰10 机39 节点电力系统上进行仿真可得到如下结论。

1）相比现有方法,本文提出的基于PMU 重要性的PMU 子集搜索方法只需要保证全网节点可观性,因此得到的关键PMU 子集数量更少,降低了PMU 子集的冗余性,大大减少了计算量。

2）自适应加权融合机制在任意可能发生的PMU 失效情况下均能有效集成未受影响的暂态评估子模型,实现对数据缺失的鲁棒性。

3）PMU 失效数量是影响模型性能的主要因素,由于考虑了特征的重要性,本文提出的暂态稳定自适应集成评估方法在准确性、鲁棒性上均优于现有评估模型。

本文考虑的PMU 子集搜索是针对全网节点可观性进行研究的,没有考虑到风险最小化的问题,关注主要PMU 失效场景并构建PMU 子集搜索优化模型是未来研究的重点。此外,随着深度强化学习的发展,将其应用于实时紧急控制并形成基于PMU实时量测的暂态稳定评估与控制框架是一个具有潜力的方向。而电网模型参数和实际存在一定偏差的问题,可以通过离线施加扰动的方式校核时域仿真模型响应数据和PMU 数据,使得两者动态响应过程接近。这种方式得到的数据和历史PMU 数据一起训练机器学习模型,可以解决实际应用偏差的问题,这也是后续需要探索的内容。

本文审理过程中审稿人与作者的讨论见附录B。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。