加强算法指导 提高学生口算能力

【摘 要】《义务教育数学课程标准》明确指出，口算是笔算、估算、简便计算的基础，也是计算能力的重要组成部分。口算作为学习数学的基础，具有方便、快速、灵活等优点，且在实际生活中也具有广泛的用途，因此提升学生的口算能力是低年级数学教学的重要任务之一。本文主要以一年级口算教学为例，浅谈提高学生口算能力的措施，以供广大教师参考。

【关键词】小学数学;算法指导;口算能力;策略

【中图分类号】G623.5  【文献标识码】A  【文章编号】1671-8437（2021）28-0179-02

运算能力作为重要的核心素养之一，是指根据法则和运算律正确地进行运算的能力。培养学生的运算能力有助于学生理解算理，寻求合理简洁的解决运算问题的途径。而在低年级的数学教学中，运算以口算的形式为主，因此教师在低年级教学中应注重培养学生的口算能力。另外，学生在口算时需要经历比较复杂的心理活动，所以提高学生的口算能力对提高学生的注意力、记忆力、灵活性以及逻辑思维能力都是有益处的。笔者认为培养学生的口算能力需要从多方面入手，接下来从以下几个方面谈谈个人的看法[1]。

1   引入图例，理解算法

低年级学生虽然有了一定的生活经验，并且能在掌握的概念基础上进行初步判断和推理，具有一定的抽象概括能力，但是其思维仍旧是以形象思维为主，无法直接理解较为抽象的知识。而且他们大多活泼好动，注意力保持的时间较短。所以在教学中，引入图例既能吸引学生的注意力，又能让学生在具体事物的辅助下，更好地掌握新知识[2]。

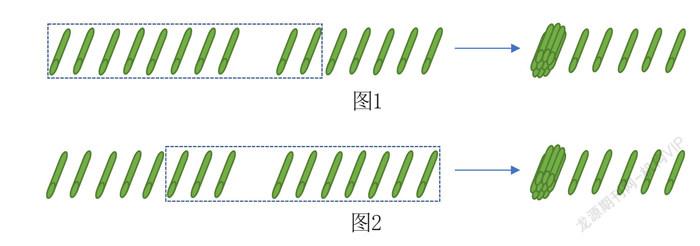
如在教学“8、7、6加几”时，书中例题为口算“8+7”。教师可要求学生用小棒摆一摆，来表现自己的想法。

（1）从右边的7根小棒中拿出2根，放入8根小棒中合成10根（如图1所示）。

（2）从左边的8根小棒中拿出3根，放入7根小棒中合成10根（如图2所示）。

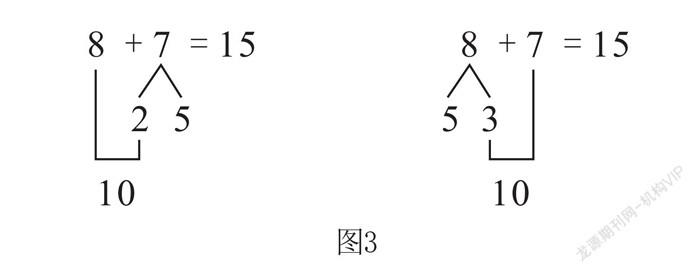
学生自己会动手操作，但不能马上抽象出实践过程背后蕴含的算理。而结合这两个图例，学生能很快写出以下两种算法（如图3）。

在学生动手操作的基础上引入图例，能直观形象地引导学生掌握“凑十法”，掌握口算的不同算法。

2   理解算理，掌握算法

口算教学并不是只要学生能算出正确的结果就行，还需要引导学生理解算理。那么算理是什么呢？算理是客观存在的规律，是计算过程中的道理，它解释了为什么这样算。算理是算法的基础，所以在帮助学生掌握算法之前，教师需要引导学生理解算理[3]。

如在教学“十几减9”时，书中例题为口算“13?9”。先让学生用小棒摆一摆，再表述自己的想法，可能会出现以下几种情况：①从13根小棒中，一根一根地取，取出9根，还剩下4根：13?1?1?1?1?1?1?1?1?1=4。②将13根小棒摆成10根和3根，先取走3根，再从10根中取出6根，还剩4根：13?3=10，10?6=4。③将13根小棒摆成10根和3根，先从10根中取出9根，剩下1根与原来的3根合起来就是4根：10?9=1，1+3=4。然后教师可追问这几种算法的共同点，引导学生发现并理解无论是哪种算法，都从10里减去了一些，也就是当个位的3不够减时，要从十位借1来进行计算。紧接着出示14?9、15?9、16?9让学生口算，在之前的活动基础上，学生能很快口算出答案，再追问这几道口算题在口算时有什么共同点，引导学生自己归纳出计算过程：十几减9，当个位不够减时，都要从十位借1当作10来进行口算。学生通过自主归纳算理，对十几减9的算法有了更深层次的理解，能提高计算的正确率，提高口算能力[4]。

3   知识迁移，运用算法

“迁移”是学生在学习过程中经常出现的一种心理现象，数学知识的连贯度高、系统性强，口算部分的新旧知识之间联系紧密。所以在教学中，教师可以根据教材内容前后的联系以及学生的思维特点，运用迁移的特性，适时为学生提供相适应的材料，使学生主动思考、自主探索并掌握算法。

如在学习“100以内的退位减法口算”时，口算例题为“34?8”。在探究新知前，笔者先安排了复习环节：口算28?2、47?3、56?6、89?5、16?7、12?8。在学生回答之后，追问：“前面四道口算题都是什么类型的口算？你是怎么算的？”随后引导学生归纳：两位数减一位数，先算个位上几减几，再加上剩下的几十。揭示课题后出示34?8，学生通过复习环节的铺垫，独立思考、自主计算后可以得出算法：先算14?8=6，再算20+6=26。

口算知识之间的联系比较紧密，虽然进位、退位等会使口算过程变得更加复杂，但它们的算理基本相同，算法可以迁移。这样通过复习不退位减法的口算过程，能唤起学生的相关知识基础和学习经验，再设置20以内的退位减法的口算，引导学生将已经掌握的算法迁移到退位减法中，真正发挥学生的主体作用，在提高其口算能力的同时，也提高了他们的学习能力。

4   建构模型，反思算法

什么是数学模型？徐利治先生在《数学方法论选讲》一书中谈到，“数学模型”（Mathematic Model）是一个含义较广的概念，粗略地讲，它是指参照某种事物系统的特征或数量相依关系，采用形式化数学语言，概括地或近似地表达出来的一个数学结构。从广义上说，一切数学概念、数学理论体系、数学公式、数学方程以及由之构成的算法系统都可以称为数学模型[5]。在教学中，教师也可以适当引导学生对学过的口算知识进行系统化地比较、归纳，尝试建构简单的算法模型，来帮助学生提高口算速度和正确率。

如在教学“20以内的进位加法”时，在引导学生理解算理掌握算法的基础上，出示口算题：9+5、9+6、9+7、9+8。学生口算后，教师追问：“这几题都是关于数字几的口算？结果有什么共同点？仔细观察另一个加数以及和的个位上的数字，你有什么发现？”通过三个连续的问题，引导学生讨论发现9加几的口算规律：和的十位是1，个位比另一个加数小1。再出示8加几的口算题，引导学生讨论发现8加几的口算规律：和的十位是1，个位比另一个加数少2。在此基础上，学生能很快推理出其余加数的口算规律。再引导学生归纳建模：几加九进十减一、几加八进十减二、几加七进十减三、几加六进十减四。根据加法交换律，其余数字便能巧妙记忆。之后在学习“100以内进位加法”时，可以进一步引导学生掌握不管多大的两个数相加，它们都是将20以内进位加法的法则作为基础，所以只需要先观察两个加数的个位，按照构建的算法模型进行口算即可。

引导学生通过分析比较、讨论概括、回顾归纳等方式，体会知識间的内在联系，形成程序性知识，既能帮助学生建立完整的知识体系，又能让口算方法变得合理简洁，在提升学生口算能力的同时，还能培养学生的推理能力和模型思想。

教师在进行教学时需要注意，任何一个学科的学习都是一个漫长的、一点一滴积累的过程，口算亦是如此。在教学时教师不能盲目地进行“题海”战术，而需要针对学生的年龄特点和学习需求，开展相应的教学活动，加强算法指导，才能让低年级的学生学得更轻松、更自主，进而提升学生的口算能力，增强学生的数学素养。

【参考文献】

[1]杜翠兰.加强算法指导，提高口算教学实效[J].文理导航，2020（11）.

[2]蔡薇.小学低年级学生口算能力的培养分析[J].中国校外教育，2020（2）.

[3]张润莲.小学低年级学生数学口算能力的培养策略[J].西部素质教育，2019（20）.

[4]陶玲.小学数学教学中培养学生口算能力的措施研究[J].数学学习与研究，2019（18）.

[5]徐利治.数学方法论选讲[M].武汉：华中科技大学出版社，2020.

【作者简介】

顾梦婷（1990～），女，汉族，江苏常熟人，本科，中小学二级教师。研究方向：数学教育。