自航式诱饵捷联惯性系统构建与导航控制参数解算

孙权

（海装广州局驻昆明第一军代室，云南 昆明650107）

自航式诱饵（下简称诱饵）欺骗来袭鱼雷和敌方声呐，可掩护我潜艇机动规避，对于潜艇生存具有重要意义。目前诱饵朝着大航程、尺度模拟、诱杀型方向发展，这要求诱饵航行中能精确进行导航和控制，而诱饵目前控制导引精度不高。

主要原因是传统航向陀螺漂移误差较大；不能完全补偿地球自转影响；摆式加速度计、垂直陀螺给出的姿态角不精确；受浪涌影响，陀螺启动瞬间受各种干扰，随机漂移较大，加剧降低航向角和姿态角精度；诱饵速度一般由螺旋桨或电机转速折算，精度低，积累误差大[1]。

而捷联惯性技术具有许多优点：导航控制参数解算时考虑了地球自转和载体相对地球运动，其航向角、姿态角、速度精度较高；大幅度地降低了陀螺启动时间，可缩短系统准备时间；能提供更多且为数字化的导航控制参数，有利于应用数字滤波技术进一步提高参数精度；克服了传统敏感元件大角度测量限制，有利于解决敏感元件输出不正常引起的非控段问题；较大程度上减少了敏感元件复杂性，便于维护[2-3]。

1 诱饵捷联惯性系统构建

诱饵捷联惯性系统由惯性测量组件和导航计算机组成，惯性测量组件包括陀螺和加速度计。陀螺测量载体相对惯性坐标系（i系）在载体坐标系（b系）三个轴上的角速度上角标b表示角速度在载体坐标系上的投影。陀螺信号经采样送至导航计算机，误差补偿后进行姿态矩阵（也称捷联矩阵）计算，再利用即时值计算首向角H、俯仰角θ和横滚角γ，由首向角可进一步计算航向角。与此同时，加速度计组件测量沿载体坐标系三个轴的加速度信号，输入导航计算机，经误差补偿后，通过姿态矩阵转换成沿平台坐标系各轴的加速度信号（本文平台坐标系取为地理坐标系），然后进一步计算即可得到诱饵速度及其位置。

2 诱饵捷联惯性系统控制参数解算

2.1 姿态矩阵计算

诱饵载体坐标系OXbYbZ（bb系）可由地理坐标系OXtYtZt（t系）绕坐标轴依次旋转H、θ、γ三个角度得到，H、θ、γ为诱饵首向角、俯仰角、横滚角，t系到b系的变换矩阵为：

根据刚体定点转动理论，载体坐标系相对地理坐标系的转动还可通过四元数法来表示[4]。设四元数q表示b系相对t系之间的转动，q=q0+q1ib+q2jb+q2kb，其中ib、jb、kb为四元数向量部分的基，其方向与载体坐标系三个轴一致。

四元数q与捷联矩阵的转置矩阵Tbt的关系为[2]：

q的即时值可由下式计算：

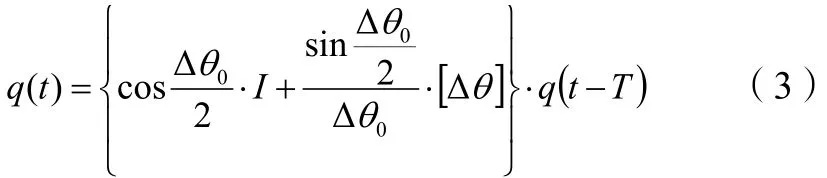
式（3）中，q（t）、q（t－T）分别为时间t和t－T时刻的四元数，T为导航控制参数解算周期，［Δθ］和Δθ0分别为：

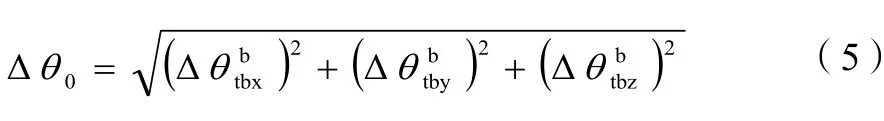
式（7）中，ωie为地球自转角速率，L为诱饵纬度，计算公式如下：

式（8）中：Vx、Vy即为诱饵运动速度在地理坐标系中分量；R为地球半径。

2.2 诱饵航向角及姿态角计算

诱饵首向角H取值范围为［0.2π］，俯仰角θ为［-π/2，π/2］，横滚角γ为［-π，π］，设诱饵发射瞬间航向基准坐标系的OXS轴与北向夹角为H0，考虑到诱饵航向取值为［-π，π］，则诱饵航向为：

2.3 诱饵速度计算

在指北方位系统中，惯性导航系统基本方程为[5]：

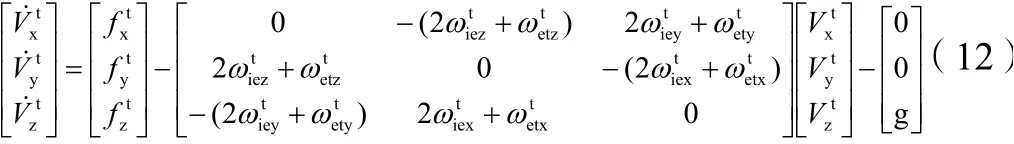
2.4 诱饵深度计算

诱饵深度可由诱饵垂直方向速度分量积分而得：

2.5 诱饵位置计算

诱饵经度λ、纬度L可采用如下公式计算：

注意，采用公式（13）计算的深度是发散的，实际工程中可以采用深、浅水压力组合传感器对诱饵深度进行测量的。

3 结语

在诱饵中通过惯性测量组件和导航计算机构建起捷联惯性系统，进行诱饵航向角、姿态角、速度、深度、位置等导航控制参数解算，可以提高航向角、姿态角等控制参数精度，降低陀螺启动时间，降低成本，提高可靠性和维修性，有利于提高诱饵机动性和精确制导，有利于诱饵实现大倾角下潜和大角度旋回，迅速达到航行深度开展对抗，有效欺骗敌方声呐和来袭鱼雷，提高作战效能。