地物三维结构的像元混合辐射响应

崔文煜,汪兰霞,2,易维宁∗

(1中国科学院合肥物质科学研究院安徽光学精密机械研究所,中国科学院通用光学定标与表征技术重点实验室,安徽 合肥 230031;2中国科学技术大学,安徽 合肥 230026)

0 引 言

目标特性是目标成像探测识别的重要基础[1]。以往的目标特性研究多聚焦于目标表面材质反射率、光谱特征、方向反射特性等本征属性。而在光学成像探测系统中,目标三维结构导致的多几何面材质差异、反射极性差异以及相互遮蔽等作用[2,3],使其在像元尺度上表现出的综合辐射响应与其表面近距离实测反射特性存在较大差异,是目前基于光学成像探测进行目标特征提取和识别的难点之一[4]。因此,建立辐射仿真模型并准确计算三维目标在像元尺度上的综合辐射响应对于目标图像特征的预测十分必要[5],而该建模研究理论上可归结为异质异构地表的混合像元模型问题。

混合像元模型主要分为线性模型和非线性模型。线性混合模型是将像元混合光谱看成是像元内各组分光谱的面积加权线性组合,认为光线在像元组分间不发生相互作用,混合光谱是在各个端元光谱进入传感器后形成[6,7]。但受到大气散射、地形起伏、目标表面粗糙度等因素影响,像元内部组分间多次散射效应加剧,理论上来说,非线性光谱混合模型更加符合实际情况[7]。然而,在实际应用中非线性混合模型在一些应用场景下并未显现良好的适用性,而线性混合模型由于更加简单,虽然存在误差,但在混合像元分解研究中仍得到广泛应用[8−10]。非线性模型基本原理是将像元内多个端元之间的复杂作用归结为多次散射。在实验和建模中,多将像元中各端元视为朗伯特性平面,主要统计各平面端元的面积比例和拓扑结构等对整体反射率的非线性作用因子[11,12]。

在高分辨率遥感普遍应用的情况下,地物细节和三维结构凸显,像元内各端元不再符合平面假设,应考虑其异构异质引起的方向辐射、阴影遮蔽、结构分布等综合作用。针对三维异质混合像元模型进行了初步研究,分析了三维结构在混合像元形成过程中的影响因素。鉴于线性混合模型较贴近遥感传输理论且方便实用,根据外场实验测量数据,在线性模型的基础上进行了改进,引入方向、阴影、分布修正因子,通过模型计算结果与实测反射率值的比较,证明模型具有一定的准确性。

1 混合像元建模原理

1.1 混合像元形成

成像型遥感器的各像元光电响应值表征其对应地面瞬时视场范围内所有地物辐射信息的综合响应,其中每一种具有特定光谱辐射特性的单纯地物,都是混合像元的基本组成部分—端元[13]。图1为混合像元形成原理示意图,图中IFOV是瞬时视场(Instantaneous field of view),即成像系统中单个像元对应的视场。由图可知,像元内不同端元在遥感过程中的混合作用包括三个部分:1)不同端元反射辐射的零视距混合效应;2)不同端元的反射辐射经大气交叉辐射作用在遥感器入瞳处的混合效应;3)遥感器成像调制的混合像元效应。因此混合像元的总表观辐射量并非不同端元辐射按面积比例的线性组合。

图1 混合像元示意图Fig.1 Schematic diagram of mixed pixel

鉴于混合像元形成过程的复杂性,先对第一部分混合效应即不同端元反射辐射的零视距混合效应进行分析论述。对于高分辨率成像而言,小尺度下地物细节凸显,像元视场内的地物几何构造、异质构成、阴影组成、背景辐射等因素是混合像元建模考虑的重点内容。

1.2 传统线性混合模型

线性混合模型对遥感辐射过程进行了简化,其将混合像元内各端元地物视为朗伯平面,各端元反射光线在近地表的相互辐射以及在大气传输过程中的交叉散射作用也予以忽略,或用误差项经验修正;并且将遥感器也视为理想成像系统,像元各端元辐射能量在焦平面上单个像元内线性累加。在这种假设下,像元混合反射率的计算即将瞬时视场内各端元地物的反射率根据其面积占比进行线性累加。

线性混合模型计算像元混合光谱反射率的基本公式为

式中R(λ)表示像元在波长λ处的混合光谱反射率,n是端元总数,αi表示像元内第i个端元在像元瞬时视场范围内所占的面积比,ρπ(i,λ)表示像元内第i个端元在波长λ处半球空间光谱反射率,e是综合误差项[14]。

在遥感信息处理的实际应用中,对于平整均匀的地表,在大气能见度高、成像遥感器性能良好的情况下,端元间的交互辐射作用较弱,线性混合模型与实际辐射传输过程较为一致。但是式中给出的单一误差项还是难以准确表征和修正多端元间交互辐射、地-气耦合、邻近交叉散射等影响。

2 三维结构异质混合像元模型

高分辨率遥感影像对地表细节具有更强的刻画能力,因此其混合像元效应需考虑地物三维异构和异质情况。在线性模型的基础上,考虑像元内地物的辐射方向性、阴影面积、背景辐射等因素,建立三维异质混合像元模型。

2.1 基于方向性因素的改进模型

自然地物对入射光线的反射强度在半球空间内也并非均匀分布,具有一定的方向特性。这种方向反射特性一般由双向反射分布函数(BRDF,Bidirectional reflectance distribution function)来确定地物在某方向的反射率与光线入射角的数学关系。为分析三维目标的方向反射特性对混合反射率的影响,利用美国ASD公司(Analytical Spectral Devices.,Inc)生产的便携式地物波谱仪FieldSpec 4,垂直向下观测一个8 cm×8 cm×16 cm四棱锥的混合反射率,三维目标方向反射特性对混合反射率影响效果的测量实验系统示意图如图2所示。

图2 三维目标方向反射特性对混合反射率影响效果的测量实验系统示意图Fig.2 Schematic diagram of experiment system for measuring the mixed reflectivity influenced by surface BRDF of 3D object

四棱锥各个斜面的法线方向与光谱仪观测方向、光源入射方向的相对几何关系有差别。保持四棱锥中心点位置和光谱仪观测角度不变的情况下(短时间的太阳光源位置可视为固定),按三种水平方位放置,如图3所示。

图3 测量对象摆放方位示意图和实物图。(a)摆放角度1;(b)摆放角度2;(c)摆放角度3;(d)实物照片Fig.3 Schematic diagram and photograph of the placement of measuring object.(a)Placed by angle 1,(b)placed by angle 2,(c)placed by angle 3,(d)the photograph

利用非成像型地物波谱仪FieldSpec 4测量四棱锥不同摆放方位下的混合光谱。地物波谱仪的光谱测量范围为350～2500 nm,光谱分辨率为3 nm(可见近红外波段)、8 nm(短波红外波段)。其光线探头视场角β有8°和25°可选。测量高度h=90 cm,根据视场面积计算公式R=htan(β/2)可知,采用25°的光纤探头,则对应地面观测面积为半径R=20 cm的圆。因此FieldSpec在本实验的探测区域可看做单像元瞬时视场,采集得到的反射率值可视为像元混合光谱反射率。测量结果如图4所示。

图4 三维结构像元的多角度综合反射率光谱曲线Fig.4 Reflectance spectrum curve of 3D structure pixel on multiple angles

三维物体的各个面虽然材质相同,但法线角度不同,因其方向反射特性,在探测器入瞳处的表观反射率也不一样。模拟含有三维地物的混合像元形成过程中,除了按材质种类划分端元,三维地物各个面向探测器的投影平面也视为端元成分进行计算,各端元反射率应根据对应材质的方向反射函数得出,即

式中ρ(θi,φi,λ)表示第i个端元面向探测端投影方向(θi,φi)的光谱反射率值。

2.2 基于光照阴影因素的改进模型

多数情况下,像元瞬时视场内含有三维地物的阴影区域,在分辨率较高时,阴影面积比例相对较高,如图5所示。阴影区域可能与周围物体是同种材质,但其反射辐射计算方法不能按光源直接照射条件下反射辐射计算。根据上述分析,可将像元瞬时视场内阴影区域也视为相应的端元,混合像元模型为

图5 混合像元中光照阴影作用示意图Fig.5 Schematic diagram of light and shadow effects in mixed pixel

式中ri表示端元i的阴影系数。若端元i不是阴影区域,则ri=1;若是阴影区域,ri等于同时刻的漫总比q乘以一个立体角修正系数η,即ri=qη。添加立体角修正系数η的原因是阴影区域接收的漫射光并非完全来自半球空间,其中有被物体遮挡的部分,如图6所示。

以阴影区域边缘的点为例,阴影区域中各个点(可视为微分面元ds)接收到的漫射辐射立体角为

式中Ωds是图6中微分面元ds接收天空漫射辐射的立体角,θ、φ分别是漫射辐射受到遮挡立体角的俯仰和方位张角。面积为As的阴影区域总反射辐射功率为

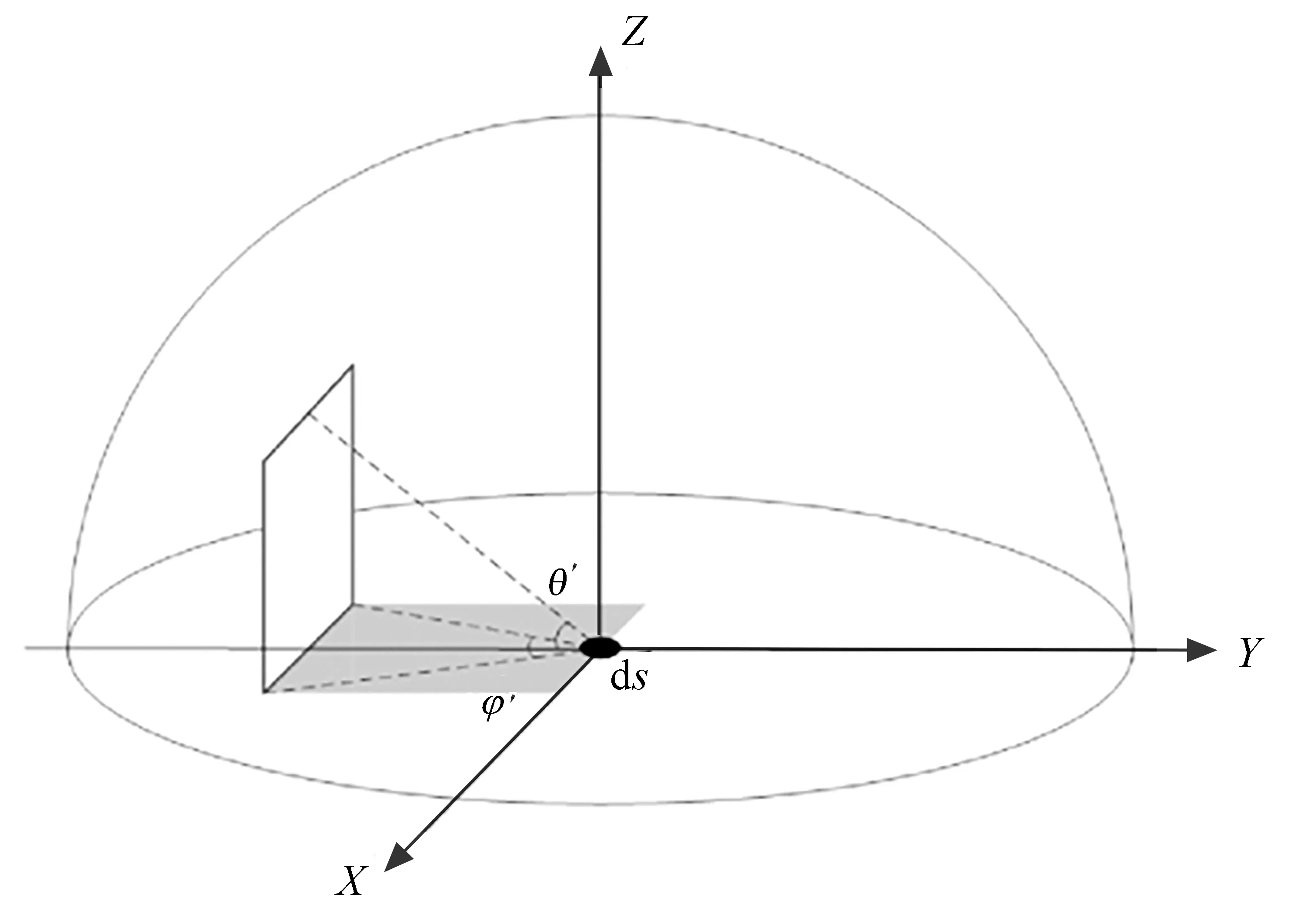
图6 混合像元中阴影区域天空漫辐射立体角空间示意图Fig.6 Schematic diagram of the solid angle of sky scatter radiation received by shadow area in mixed pixel

式中ρ是阴影区域材质的反射率,Esky是天空漫射辐照度,Esum是总辐照度,漫总比q=Esky/Esum。

像元中阴影区域端元面积较小,将其等效为方格形状,且取微分面源点(u,v)为阴影区的中心点,根据二重积分中值定理去除式(5)的积分符号,得到立体角修正系数为

2.3 基于端元分布因素的改进模型

为了分析像元中端元分布对混合反射率造成的影响,设计了如图7所示的实验系统。与图2所示的实验系统类似,同样是利用地物波谱仪垂直向下进行测量。测量目标是白色靶标,其上覆盖黑色绒布。黑布中间裁剪出圆洞,圆洞中心对准光谱仪视场中心。光谱仪在进行一次测量后,扩大圆洞半径再次裁剪后测量。这样,光谱仪探测到的是不同面积白色靶标与黑色背景的混合反射率光谱。

图7 三维结构光照阴影对混合反射率影响作用的实验系统示意图Fig.7 Schematic diagram of experiment system for measuring the mixed reflectivity of 3D object influenced by sunlight and shadow

传统线性模型中,各端元在混合像元辐射贡献权重均按瞬时视场内所占的面积计算。但是各端元对混合像元反射率的贡献与其空间分布也有关系,端元组分与视场中心的单位距离不同,对混合像元反射率的贡献不同。通过分析混合像元反射率随端元组分与视场中心距离的变化规律,建立相应的混合模型,即

式中ki为端元i对应的到像元中心距离权重系数。该模型将瞬时视场按照与视场中心的距离划分为若干部分,并根据各部分所占得权重系数进行混合计算。权重系数的设定通过实验分析获得。ASD光纤探头探测视场角β为25°,探测高度固定在90 cm,光纤视场可看成单像元瞬时视场。为找出空间位置对混合反射率的影响,距探测视场中心等间隔划分探测区域:L1、L2、L3、L4、L5、L6,如图8所示。定义以L1为半径的圆形区域为A1,L1+L2的圆形区域为A2,依此类推,从L1到L6的圆形区域即整个探测视场记作A6。按照距离视场中心的单位距离划分探测区域后,依次采集木板放置在不同探测区域时的反射辐射,对组数据连续测量5次,并进行平均处理以降低随机误差及提高测量精度。测量结果反射辐射光谱曲线对比图如图9所示。由图可见,A1到A6区域混合反射辐射所占总混合辐射比例并不是按其半径倍数关系平方递增的,各端元对混合光谱的影响与其离视场中心的位置相关。

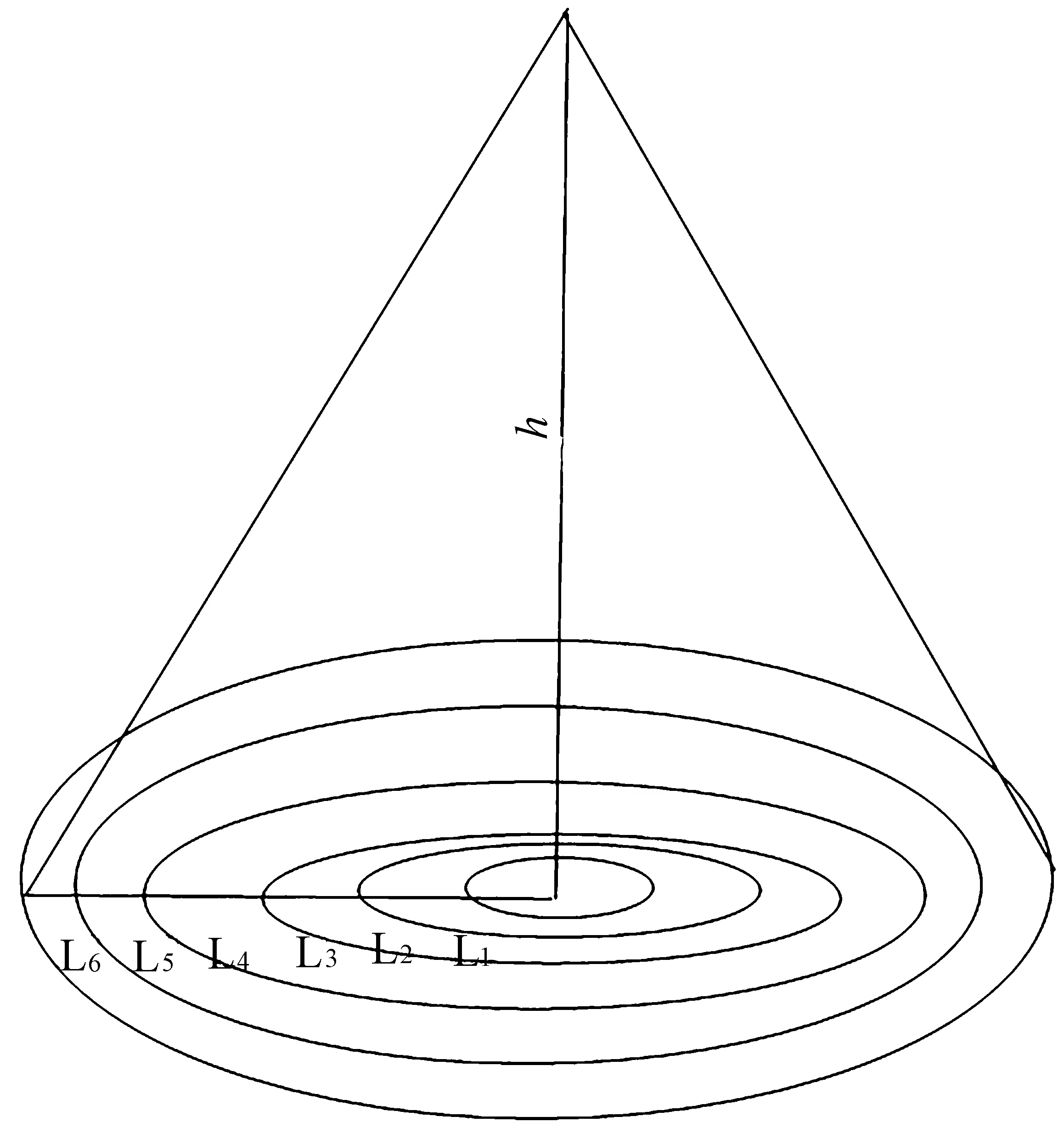
图8 探测区域划分示意图Fig.8 Schematic diagram of the detection area division

图9 覆盖不同区域的像元综合反射率光谱对比Fig.9 Comparison of pixel composite reflectance spectrum curves of different coverage areas

对不同区域混合反射辐射利用最小二乘法拟合,分析目标覆盖不同区域反射辐射与距离视场中心单位距离的关系,求出模型中各部分权重参数。通过分析光谱反射率随端元组分与视场中心距离占视场半径的比例的变化规律,得出反射率特征变化规律,即探测单位距离与探测中心距离不同,则对混合像元反射率贡献权重也不同。区域A1、A2、A3、A4、A5、A6对混合像元反射率贡献权重分别为0.09、0.30、0.56、0.81、0.96、0.97。

需要说明的是,上述权重系数仅适用于本实验系统,因为该权重系数是由成像响应机理决定,即像元的整体响应输出是地物辐射分布与传感器空间响应函数的卷积运算结果,其离散化描述为

式中D(i,j)是成像系统第i行、第 j列像元输出的电计数值,I(x,y)是瞬时视场内(x,y)处地物的辐射量,F(u,v)是传感器空间响应函数,n是将像元视场内进行离散网格划分的网格数量,(u−i,v−j)即为地物点坐标(x,y)在像面投影(u,v)到像元中心(i,j)的距离。传感器空间响应函数一般可由点扩散函数(PSF)表示,但实际应用中,通常认为单个像元面上空间响应一致(像元内空间响应的不一致性不可测,且没有实际意义),如图10所示。

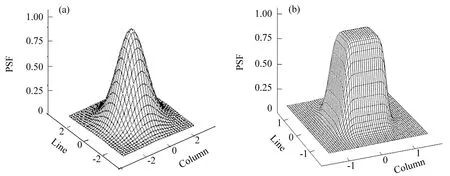
图10 成像点扩散函数示意图。(a)理论函数;(b)实际函数Fig.10 Schematic diagram of imagery point spread function.(a)Theoretical function,(b)practical function

像元的空间响应函数F(u,v)可简化为窗函数,其表达式为

式中Ad是像元尺寸。

考虑端元分布因素,混合像元辐射模型可描述为

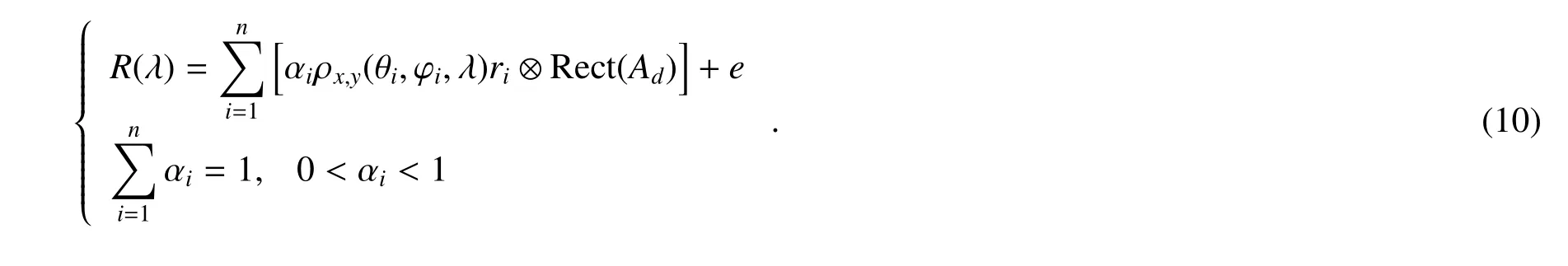
3 实验验证

利用非成像光谱仪对三维结构体进行光谱反射率测量,对结果分析可知,单像元中三维结构体的表面方向反射特性、光照阴影、端元分布等因素对像元混合反射率具有影响。在线性混合模型的基础上,通过引入方向反射因素修正系数、光照阴影因素修正系数、端元分布因素修正系数,提出了改进型混合反射率计算方法。分别利用改进型算法和线性混合模型对三维结构体的混合反射率进行计算,并将计算结果分别与实测结果对比进行精度验证,比较两种算法对于三维地物混合反射率计算的适用性。实验验证及分析流程如图11所示。

图11 实验验证及分析流程示意图Fig.11 Schematic diagram of experimental verification and analysis

3.1 方向性因素验证

在方向性影响因素验证方面,混合光谱实验对象分别为8 cm×8 cm×8 cm 和16 cm×16 cm×8 cm的两个四棱锥和黑色背景布。四棱锥表面材质的方向性反射特性已预先测得,由此分别用传统模型和改进模型计算三维物体在单元视场内的混合反射率,并与光谱仪实际测量的混合光谱反射率进行比较,以此验证改进模型的准确度及其相较于传统模型的优势。

实验过程中采用ASD光谱仪来获取混合光谱。分别利用ASD的8°和25°视场的光纤探头模拟像元瞬时视场,对四棱锥由上向下正射测量,测量高度为90 cm,得到的反射率值可视为像元混合反射率,每组数据测量5次求平均。

将四棱锥各个斜面作为混合像元的各个端元,计算各端元在光谱仪视场中的面积及其向光谱仪入瞳投影的方向反射率,并计算各端元所占权重,由此代入改进模型计算混合反射率,与实测结果进行比较,结果如图12所示。图12(a)是利用光谱仪8°光纤视场模拟和测量8 cm×8 cm×8 cm四棱锥混合光谱发射率的结果,图12(b)是利用光谱仪25°光纤视场模拟和测量16 cm×16 cm×8 cm四棱锥混合光谱发射率的结果。图中可以看出,两种模型计算的反射率光谱曲线与实测结果趋势一致,但加入方向反射特性修正的线性模型,计算结果与测量结果在量值上差别更小。

图12 含有三维几何体混合像元综合反射率光谱计算结果和实测对比。(a)8 cm×8 cm×8 cm四棱锥;(b)16 cm×16 cm×8 cm四棱锥Fig.12 Comparison between calculating and measuring results of composite reflectance spectrum of pixel containing 3D geometric solids.(a)8 cm×8 cm×8 cm pyramid,(b)16 cm×16 cm×8 cm pyramid

利用相对误差ΔR及其标准差S来定量评价模型准确度,其计算公式分别为

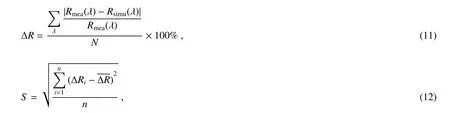
式中Rmea(λ)为在中心波长λ波段的实测混合反射率值,Rsimu(λ)为中心波长λ波段的模型计算混合反射率值,N为波段数,ΔRi为第i次模拟与测量的相对误差,为多次模拟与实测对比相对误差的均值,n是试验次数。

考虑方向反射特性影响因素的改进模型与传统线性混合模型计算像元综合反射率的误差如表1所示。从表中可以看出,改进模型比传统线性模型对三维物体的混合反射率模拟准确度有所提高。

表1 改进模型(含方向反射因素)与线性模型计算像元综合反射率误差比较Table 1 Comparison of calculating error of pixel composite reflectance between improved model(containing directional reflection factor)and linear model

3.2 光照阴影因素验证

为验证在地物光照阴影因素影响下,模型计算像元混合光谱反射率的准确性,设计实验。在暗室条件下,对两种几何体进行混合光谱反射率测量实验。实验过程中采用ASD光谱仪来获取混合反射率值,实验对象选用大小分别为16 cm×16 cm×8 cm的四棱锥、16 cm×16 cm×8 cm的长方体和黄色木质背景板。分别测量两个三维模型放置在黄色木板上的混合光谱反射率。每组数据测量5次求平均。

根据ASD光纤探测方式,瞬时视场内各端元组分如图13所示,图13(a)为长方体与黄色背景板混合示意图,图13(b)为四棱锥与黄色背景板示意图,其中S1为长方体/四棱锥在视场内所占面积,S2为木板所占区域,S3为三维目标体的阴影区域。分别计算图13(a)和图13(b)中的目标体、背景板和阴影区域在地物波谱仪视场内所占面积比例,结果如表2所示。将三维目标体向探测端的投影面以及背景木板和光照下的阴影区域作为地物波谱仪单元视场内的各个端元,分别利用改进模型和传统模型计算混合反射率,并与实测结果进行比较。

图13 像元中三维几何体在光照作用下形成阴影端元示意图。(a)长方体;(b)四棱锥Fig.13 Schematic diagram of the shadow end-members formed by light effect on 3D geometric solids in the pixel.(a)Cuboid,(b)pyramid

表2 像元中各端元组分所占面积比例Table 2 Area proportion of each end-member in pixel

根据式(11)和式(12)定量评价混合光谱模拟的精度,结果如表3所示。由表可知,考虑阴影部分影响的计算结果更符合实际情况。

表3 改进模型(含光照阴影因素)与线性模型计算像元综合反射率误差比较Table 3 Comparison of calculating error of pixel composite reflectance between improved model(containing light and shadow factor)and linear model

根据对比误差发现,参照几何光照模型考虑阴影部分的影响进行建模,虽然模拟结果误差只降低约2%左右,但这主要是因为阴影部分所占的面积比例较小,从结果可知,计算精度与阴影面积比例呈较高的正相关关系,因此对于光照倾角较大的情况,遥感成像仿真中考虑像元视场内光照阴影因素能提高仿真精度。

3.3 端元分布因素验证

为验证端元分布与探测视场中心的距离因素对混合光谱的影响及改进模型的准确性,设计实验锥体与不同颜色背景板混合实验,用线性模型和改进模型对混合像元进行建模分析,模拟结果对比如图14所示。两种方法求解的平均误差及相对误差标准差如表4所示。

由图14及表4可见,与仅按面积比例加权的线性模型模拟相比,兼顾端元面积以及与探测视场中心距离的权重系数使模型具有更高的混合反射率模拟精度。

表4 改进模型(含端元分布因素)与线性模型计算像元综合反射率误差比较Table 4 Comparison of calculating error of pixel composite reflectance between improved model(containing end-members distribution factor)and linear model

图14 三维几何体在不同底板上像元综合反射率光谱计算与实测结果对比。(a)红色底板;(b)蓝色底板;(c)黄色底板;(d)银色底板)Fig.14 Comparison between calculating and measuring results of pixel composite reflectance spectrum of 3D geometric solids on different board.(a)Red board,(b)blue board,(c)yellow board,(d)silver board

4 结 论

基于混合像元原理对地物三维结构特征的像元综合辐射特征进行了建模分析和计算。结合对三维几何体及其不同背景的测量实验,分析了方向辐射特性、光照阴影和端元分布因素对混合反射率的影响作用,并尝试基于线性混合模型加入修正因子进行改进。结果表明,较之于广泛使用的线性混合模型,改进后模型计算精度有所提高。

三维结构的实际辐射作用不止文中提出的三种因素。改进模型限于零视距成像条件,未考虑大气和传感器效应,且模型改进方法及修正因子依赖实测数据,样本数量限于实验条件有待增加,因此混合像元模型的合理性和普适性有待进一步研究和验证。

另外需要说明的是,非线性混合模型相对复杂[15],其中包含经验参数,是对全链路遥感过程的混合像元效应描述,与本研究零视距条件下的模型计算和实验测量结果无可比性,因此,文中未提及与非线性混合模型的参照对比情况。