凤凰之舟大剧院钢结构稳定设计

王再峰，孙绍东，于东晖，刘于晨

(1 青岛腾远设计事务所有限公司， 青岛 266100；2 北京市建筑设计研究院有限公司， 北京 100045)

1 工程概况

凤凰之舟大剧院的层高、层数、使用功能等基本信息见文献[1]。钢结构平面布置图和建筑剖面图分别如图1，2所示。

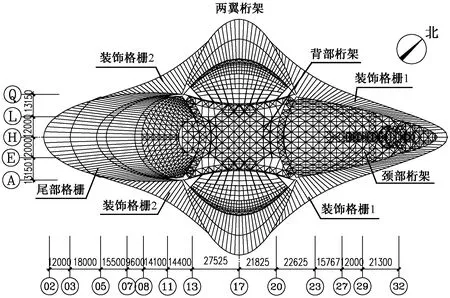
图1 钢结构平面图

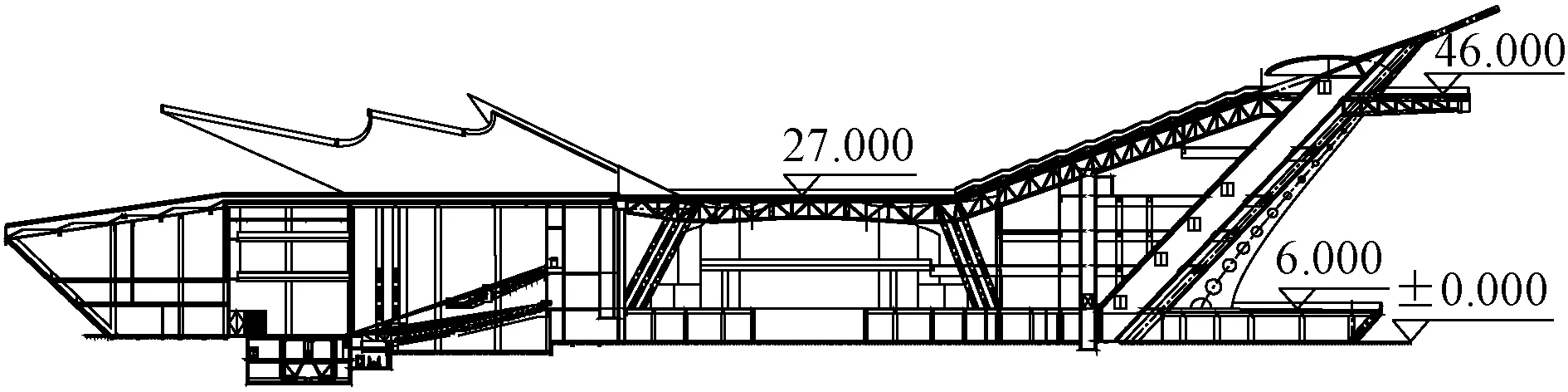
图2 建筑剖面图

结构计算模型见文献[1]，整个钢结构部分的主体可以分为：头部、嘴部、颈部、背部、两翼、尾部结构以及内部的各楼层框架几部分。颈部、尾部和两翼四个部分结构受力体系不同，但是又通过四个倾斜的拱架与背部结构连为一个整体，既保证了结构的整体刚度，也抵消了一部分因为倾斜和悬挑产生的不平衡力，使得整个结构的传力更加合理和经济。钢结构大致的传力路径如图3所示。

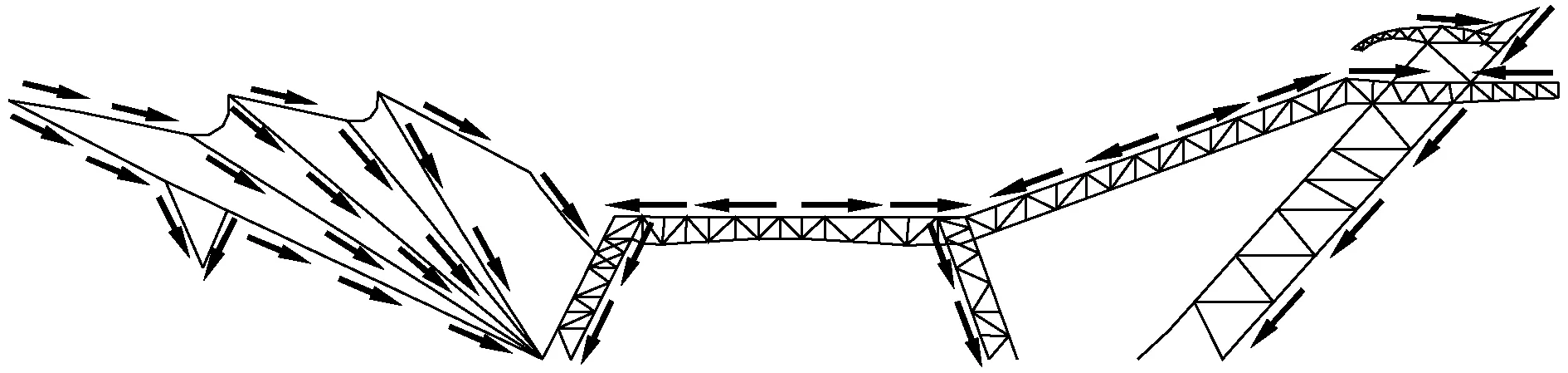
图3 传力路径图

从图3可得，结构受力比较复杂，尤其钢结构的稳定计算是结构计算的关键所在[2]。首先，作为颈部、背部和尾部结构的曲面壳体，其结构的整体稳定分析将是一个首要的关注点。其次关于颈部斜柱、尾部的拱架、颈部和两翼的装饰拱架等局部构件的稳定计算，也都是非常重要的问题。钢结构稳定设计分别采取了多种不同的方法和软件进行计算分析，并根据分析结果采取各个情况下的包络设计。钢结构整体稳定设计主要采用了软件MIDAS/Gen和ABAQUS分别进行对比分析，并且考虑到结构计算的效率和可靠性兼顾问题，本文采用了两种结构模型：纯钢结构模型和包括混凝土结构在内的整体模型。具体分析包括：1)使用MIDAS/Gen对包括混凝土结构在内的整体模型进行线性屈曲分析；2)使用MIDAS/Gen对纯钢结构模型进行几何非线性屈曲分析；3)使用MIDAS/Gen对整体模型进行几何非线性屈曲分析；4)使用ABAQUS对纯钢结构模型进行双重非线性屈曲分析。

2 整体稳定分析

2.1 线性屈曲分析

线性屈曲分析时采用的是带有底部混凝土结构的整体模型，材料均为弹性材料，将1.0恒载(包括自重)+1.0活载作为可变荷载工况，对整体模型进行线性屈曲分析。取屈曲分析前50阶屈曲模态和特征值，从而得到表1的计算结果。第1阶屈曲模态表现为尾部单层网壳部分的屈曲，屈曲特征值为7.19。其他各部分的屈曲模态见表1和图4。

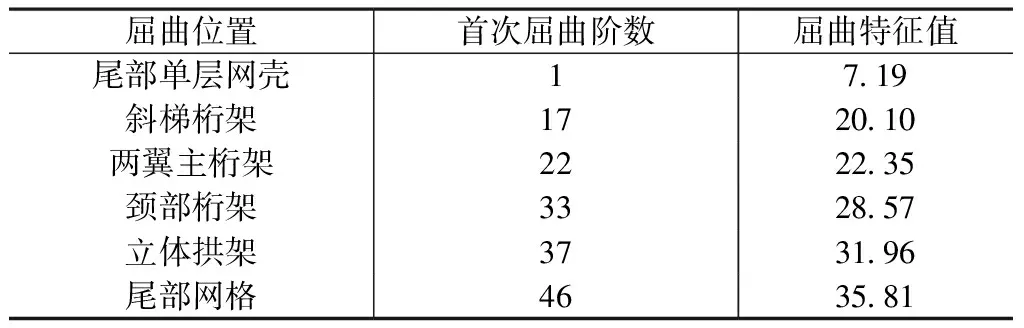
整体模型线性屈曲分析计算结果 表1

从线性屈曲分析的结果可以得到以下结论:

(1)颈部、背部和尾部结构都是有曲面的壳体结构，但是由于颈部和背部都是双层壳体，刚度较好，并且内力的传递在背部和颈部形成了较大的平衡拉力，因此颈部和背部的稳定问题并不突出。而尾部单层网壳部分，由于自身刚度低加上内力传递中并未形成过多的拉力，因此尾部的单层网壳出现屈曲分析中第1阶屈曲模态就显得比较合理了。

(2)线性屈曲分析虽然无法作为结构整体稳定设计的评判标准，但是却能够反映结构稳定问题的趋势[3]。以线性屈曲分析结果为依据，接下来需要对于包括尾部网壳部分在内的壳体结构进行进一步的深入分析，同时也应该关注颈部斜柱部分杆件的稳定问题。

2.2 几何非线性屈曲分析

考虑到线性屈曲分析中，尾部单层网壳部分率先屈曲，有必要进一步对此部分进行非线性的屈曲分析，以确定整体稳定是否满足规范要求。同时为了考察底部混凝土结构对于钢结构整体稳定的影响，分别对纯钢结构模型和包括混凝土结构在内的整体模型进行非线性屈曲分析。采用的分析软件为MIDAS/Gen，荷载工况为1.0恒载+1.0活载，并且按照最低阶屈曲模态考虑1/300的初始缺陷。分析考虑几何非线性，不考虑材料非线性。选取的控制点均为线性屈曲分析最大振动点P2，具体模型及控制点位置如图5所示。

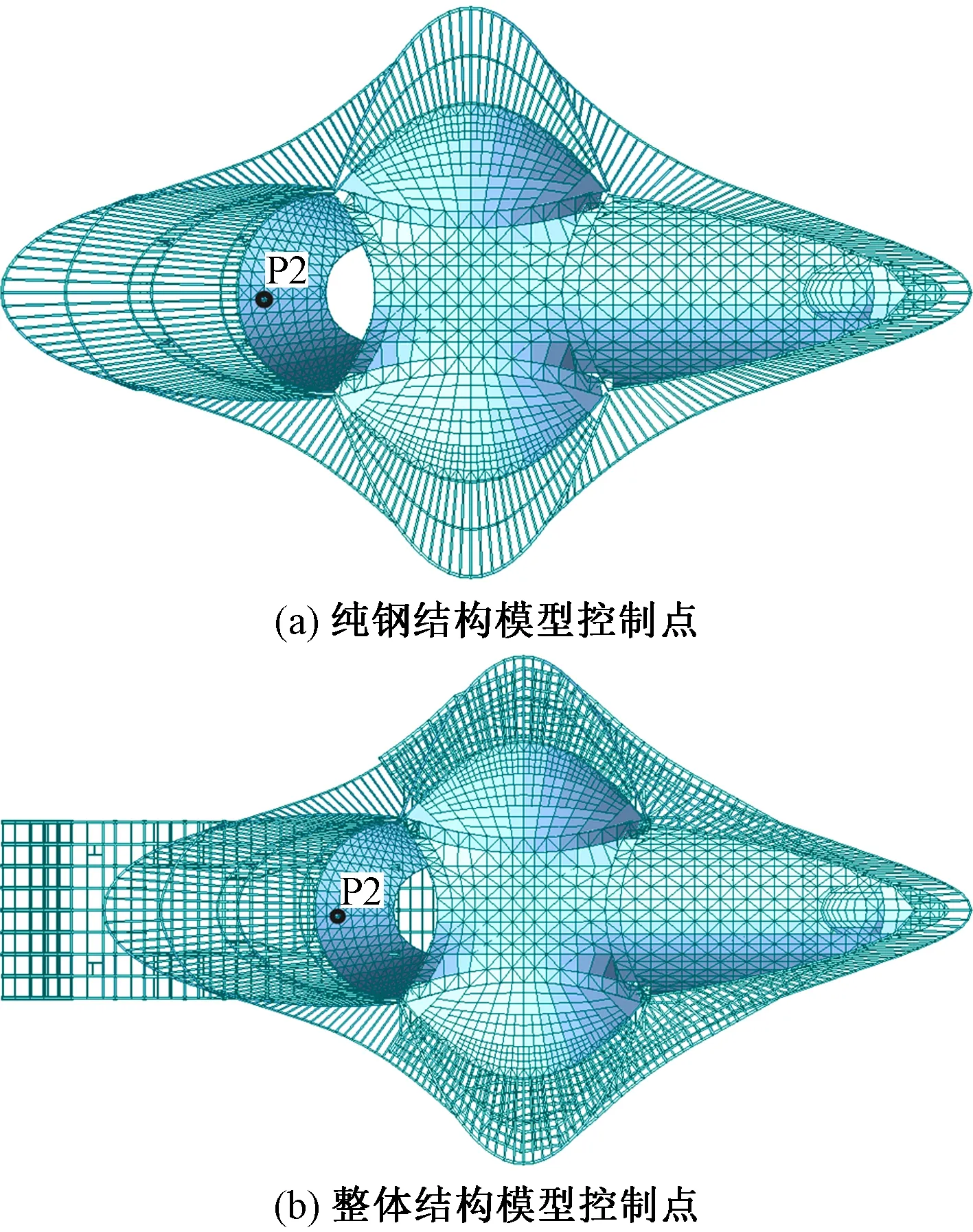
图5 结构模型及控制点位置

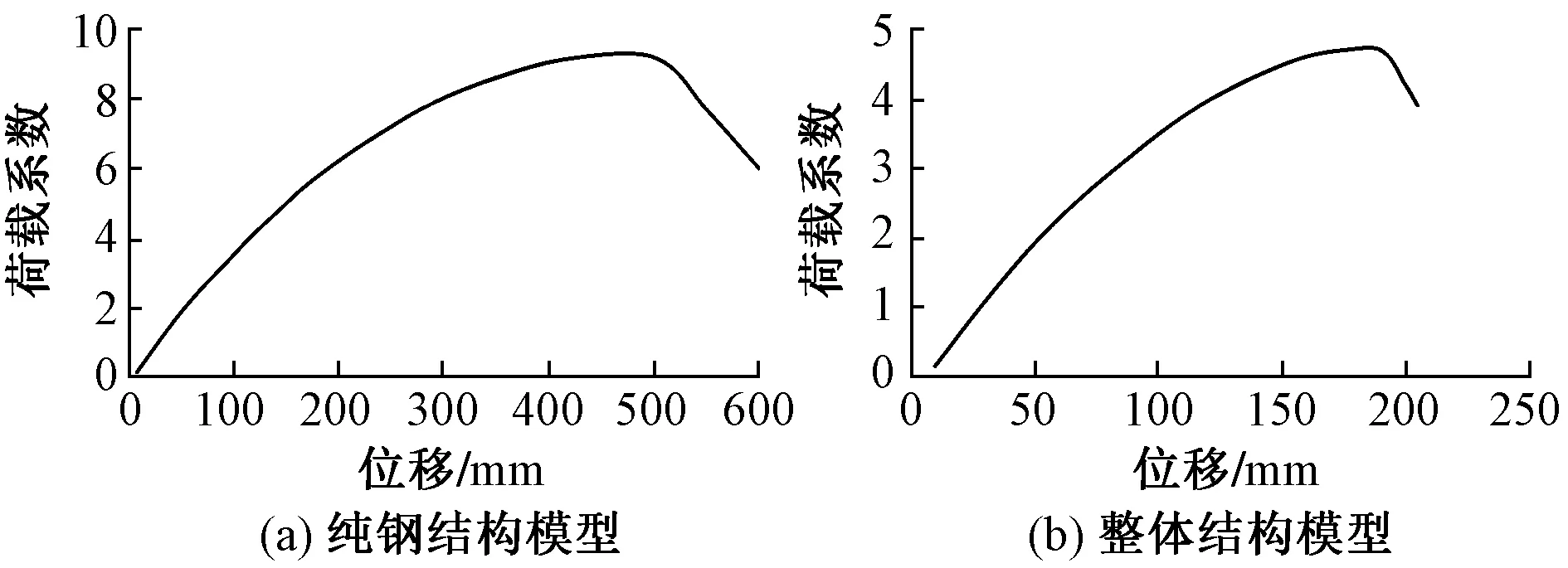
图6 荷载系数-位移曲线

通过设置合理的分析步长和收敛条件，分别计算得出如图6所示的两条非线性分析荷载系数-位移曲线。

非线性屈曲分析的荷载系数-位移曲线显示，纯钢结构模型和整体结构模型的非线性屈曲的荷载系数分别为和9.2和4.7，相差较大，此结果说明底部混凝土结构对于钢结构的整体稳定的影响还是比较明显的，按照最不利结果4.7作为最终的整体稳定安全系数，满足《空间网格结构技术规程》(JGJ 7—2010)[4]对于单层网壳几何非线性屈曲分析安全系数大于4.2的要求。

2.3 双重非线性屈曲分析

几何非线性屈曲分析的安全系数虽然满足规范要求，但是还是比较接近规范限值。为了保证结构的整体稳定性的安全可靠，设计过程中又采用软件ABAQUS进行了双重非线性屈曲分析。综合考虑计算过程的可靠性和效率性，计算模型采用的是纯钢结构模型。

考虑几何、材料非线性进行全过程分析的初始几何缺陷分布采用结构最低阶线性屈曲模态，缺陷最大值按照《空间网格结构技术规程》(JGJ 7—2010)要求取结构跨度的1/300。分析中采用的单元：梁、柱、斜撑等杆件采用纤维梁单元；板单元采用四边形缩减积分或三角形完全积分壳单元；钢材本构采用双线性随动硬化模型；选取1.0恒载+1.0活载组合作为分析用荷载标准组合。对于控制点的选取，需要综合考虑结构弹性分析和线性屈曲分析的结果，分别选取装饰格栅(控制点P1，P3)、尾部单层网壳(控制点P2)及背部拱架(控制点P4)在1.0恒载+1.0活载组合工况下位移最大的点作为考察点，得到各点荷载系数-位移曲线。双重非线性屈曲分析控制点位置见图7。

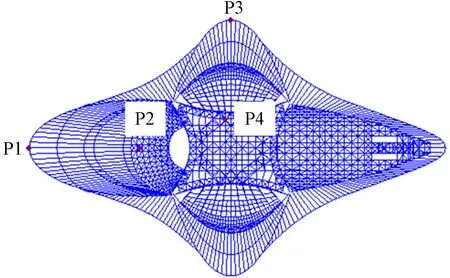
图7 双重非线性屈曲分析控制点

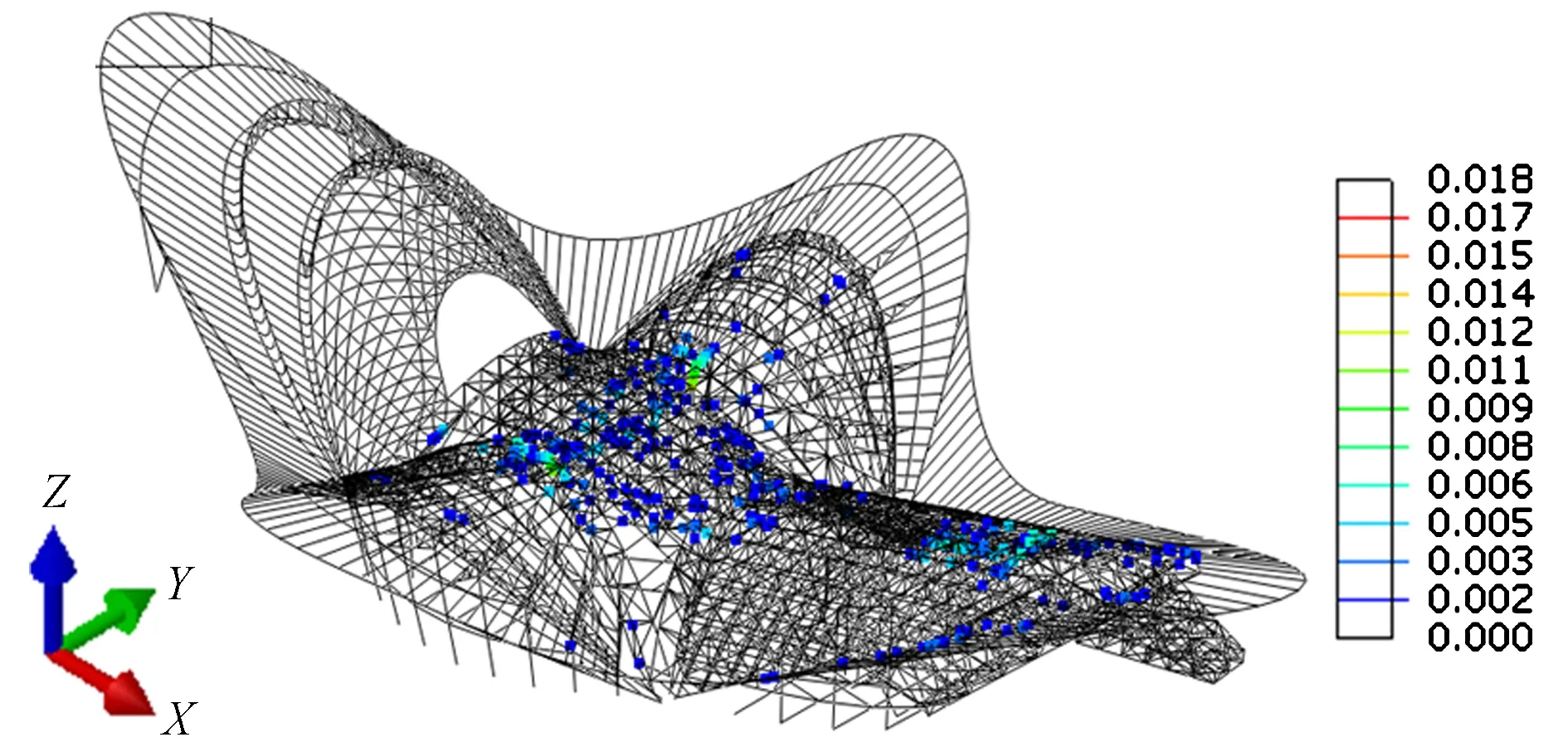
图8 4倍标准荷载组合的塑性应变

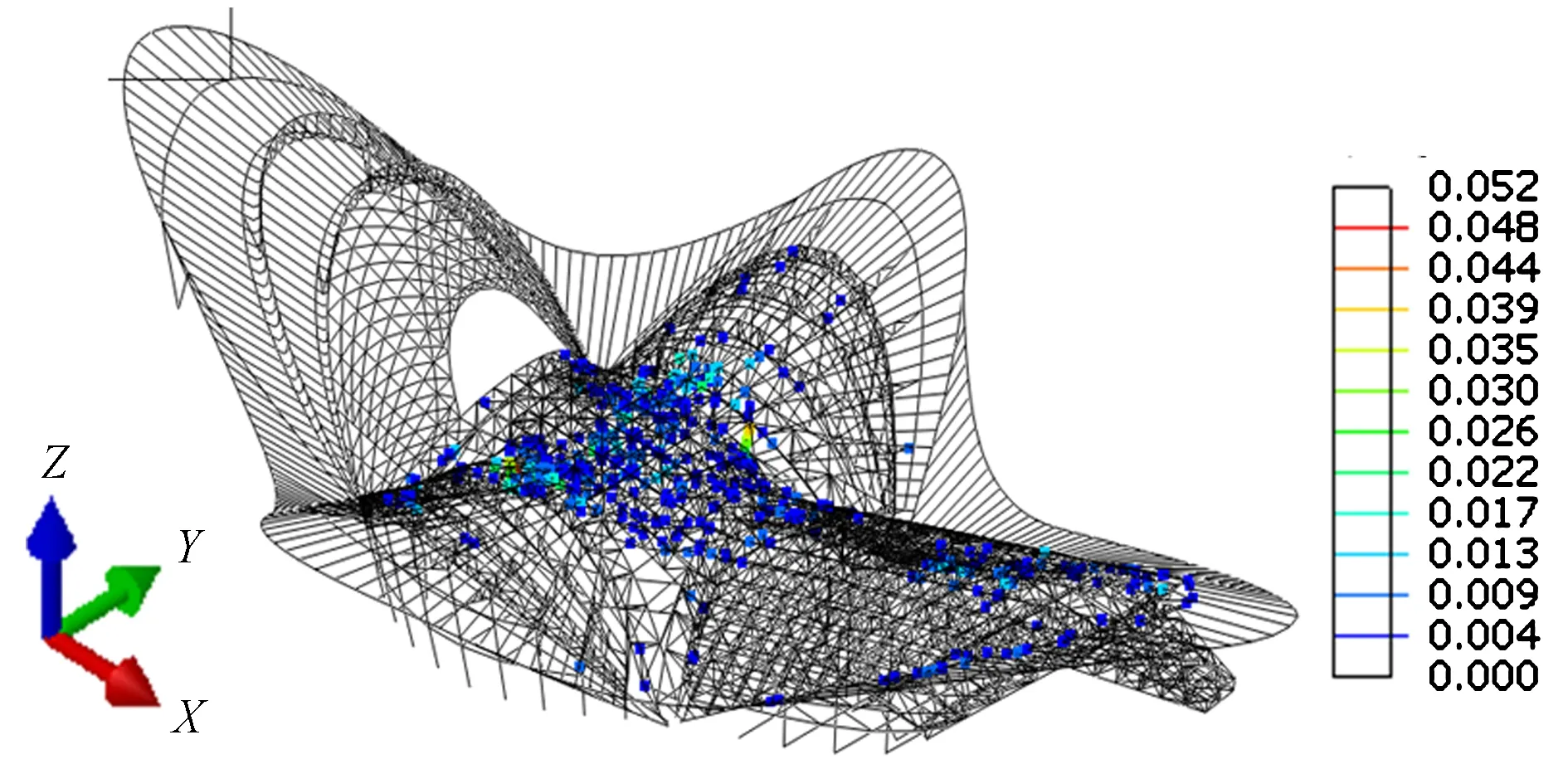
图9 5倍标准荷载组合的塑性应变图

荷载达到4倍标准荷载组合值时，结构的塑性应变见图8。从图中可得：背部及颈部结构的部分杆件进入塑性状态，最大塑性应变为0.018 。

荷载达到5倍标准荷载组合值时，结构的塑性应变图见图9。从图中可得：背部、颈部结构及两翼桁架的部分杆件进入塑性状态，最大塑性应变为0.052。

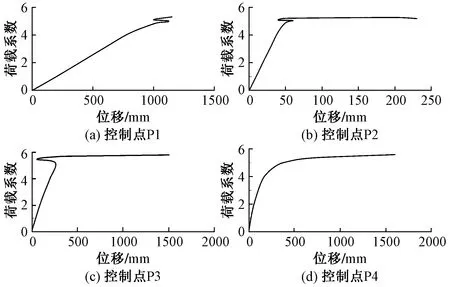
图10 控制点荷载系数-位移曲线

从图10的控制点荷载系数-位移曲线可以看到，荷载加至4倍标准荷载组合值时，背部拱架控制点P4最先出现刚度退化；在荷载加至5倍标准荷载组合值时，各控制点的刚度均出现明显的退化。由此判断结构安全系数为5，满足《空间网格结构技术规程》(JGJ 7—2010)[4]中安全系数大于2的要求。

几何非线性屈曲分析的整体结构模型屈曲系数为4.7，而双重非线性屈曲分析的纯钢结构模型屈曲系数为5.0。出现这种反差的结果是因为材料非线性和底部混凝土刚度两方面影响的结果。

3 颈部斜柱稳定计算

如图11所示，颈部结构有9根倾斜角度为48°的斜柱，这些斜柱的轴力和弯矩都比较大，受力也比较复杂，其稳定分析比较重要，需要单独考虑。为了安全起见，设计时采用屈曲分析法确定计算长度系数，并与《钢结构设计标准》(GB 50017—2017)[5]中梁柱线刚度法计算结果进行对比复核。

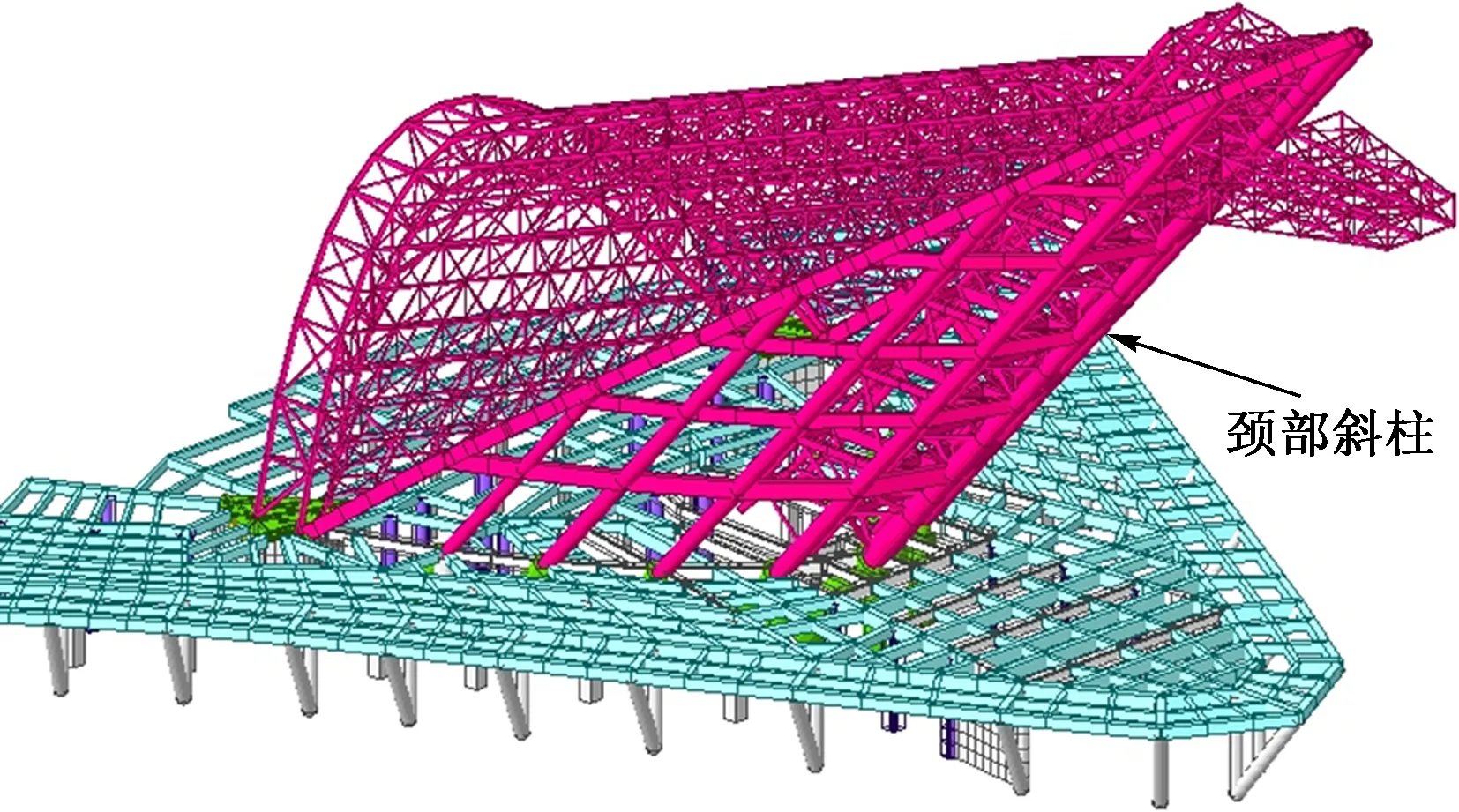
图11 颈部斜柱示意图

采用屈曲分析法确定计算长度系数的方法是钢结构设计常用的一种构件稳定设计方法[2]。斜柱在进行屈曲分析时采用的是整体模型法，从而得到斜柱的临界承载力，然后通过欧拉公式Pcr=π2EI/li2(Pcr为屈曲临界力；li为杆件计算长度；E为材料弹性模量；I为截面惯性矩)，反算斜柱的计算长度[6]，再将计算长度指定给计算模型中的对应斜柱，从而完成斜柱的稳定分析。斜柱具体的编号如图12所示，通过屈曲分析反算的斜柱计算长度系数μ1如表2所示。

图12 斜柱编号布置图

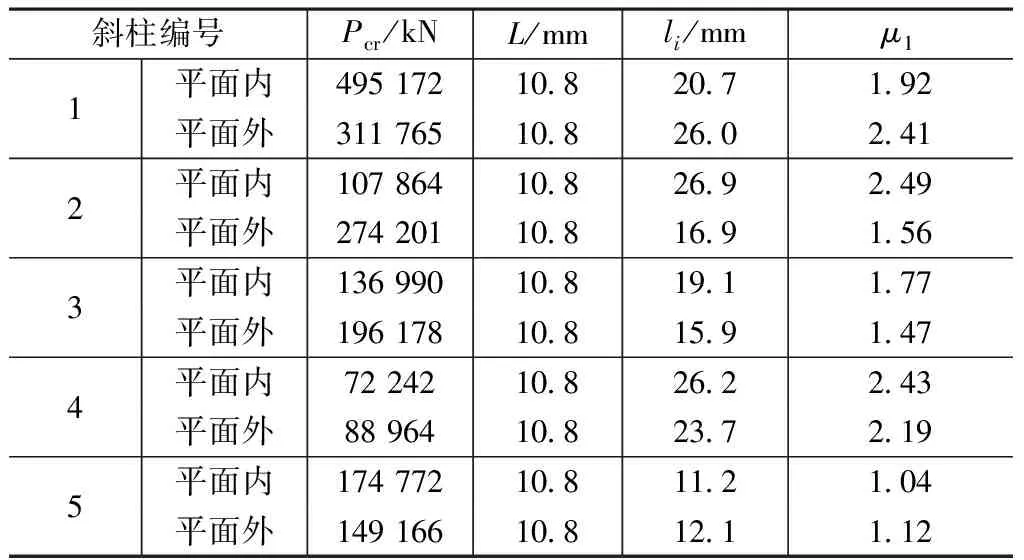
平面内计算长度系数 表2

屈曲分析法确定计算长度系数对于个别受力复杂的重要杆件的稳定计算是可行的，但是由于屈曲模态的选取具有一定的主观因素，因此在此方法基础上又采用了《钢结构设计标准》(GB 50017—2017)中的梁柱线刚度法进行计算，以此来进行对比分析。其中梁柱线刚度法计算中忽略柱子倾斜和弧形梁的影响，采用梁柱线刚度比近似计算斜柱的计算长度系数。两种方法对应的计算长度系数如表3所示。

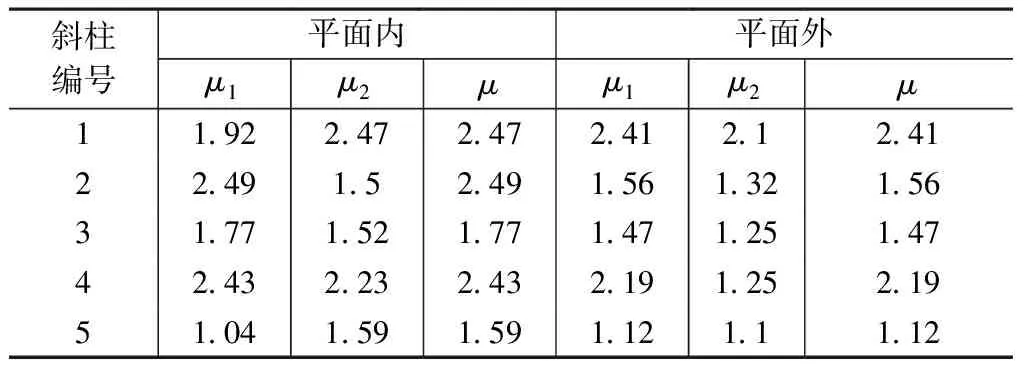
两种方法的计算长度系数对比 表3

从表3的对比结果来看，除了个别斜柱偏差较大外，大多数斜柱采用两种方法得到的计算长度系数差距不大。考虑到此部分斜柱的重要性，设计偏于安全地采用了两种方法的结果进行了包络设计。

4 结论

(1)大跨复杂钢结构的稳定分析是钢结构设计的一个难点，首先要在满足建筑方案的前提下采用合理的结构体系，从概念设计上保证结构的整体稳定和局部构件的稳定。

(2)对于曲面的壳体结构，整体稳定常常起到控制作用，尤其是单层网壳结构，至少需要考虑几何非线性进行稳定分析，确保结构安全。

(3)对于凤凰之舟大剧院的整体稳定分析，是否采用整体模型计算，对于其稳定安全系数的影响是比较大的，必须要采用合理的计算模型和软件进行更多的补充分析。

(4)对于个别受力复杂的钢柱采用屈曲分析确定计算长度系数法是可行的，但是需要进行必要的验证，减少在模态确定上的人为差别 。