高强钢筋轻骨料混凝土梁短期受弯刚度计算方法研究*
2021-12-10朱爱萍余少乐白生翔
王 涵,朱爱萍,余少乐,白生翔,赵 勇
(1 同济大学土木工程学院, 上海 200092; 2 中国建筑科学研究院有限公司, 北京 100013;3 中国建筑第八工程局有限公司, 上海 200135)
0 引言
轻骨料混凝土结构具有自重轻、保温及耐久性能好等许多优点,可在土木结构工程中推广应用。目前,我国正在推广400MPa及500MPa级高强钢筋的应用,若高强钢筋与轻骨料混凝土相结合,则能得到轻质高强的构件及结构。但由于轻骨料混凝土弹性模量较低,导致轻骨料混凝土梁的受弯刚度会低于普通混凝土梁,而配置高强钢筋的构件,其在正常使用极限状态下的钢筋应力较大,又会进一步降低构件的受弯刚度。因此,配置高强钢筋的轻骨料混凝土梁的受弯刚度问题受到了国内外研究者的关注。例如,Ahmad等[1]对6根配置Grade 60钢筋的轻骨料混凝土梁进行了受弯性能试验,并评析了美国规范ACI 318-83的相关受弯刚度计算公式,结果表明受弯刚度计算值与试验值之比的平均值为0.917;李鸥[2]对6根配置HRB400钢筋的高强陶粒混凝土梁进行了受弯性能试验,根据《轻骨料混凝土结构技术规程》(JGJ 12—1999)(简称轻骨料混凝土规范JGJ 12—1999)的公式所得短期刚度计算值与试验值相比偏小,两者之比的平均值为0.746;归强[3]、银俊[4]分别进行了3根和8根配置HRB400钢筋的高强陶粒混凝土梁受弯性能试验,认为按《轻骨料混凝土结构技术规程》(JGJ 12—2006)(简称轻骨料混凝土规范JGJ 12—2006)公式计算的短期刚度与试验值吻合较好,3根和8根配置HRB400钢筋的高强陶粒混凝土梁的短期刚度计算值与试验值之比的平均值分别为0.946和0.952。
由于缺少配置HRB500高强钢筋轻骨料混凝土梁受弯性能试验研究,轻骨料混凝土规范JGJ 12—2006的短期刚度公式能否适用于配置HRB500高强钢筋的轻骨料混凝土受弯构件值得商榷[5]。为此,本文进行了配置HRB500高强钢筋轻骨料混凝土梁的短期刚度试验,结合搜集的国内外配置高强钢筋轻骨料混凝土梁的短期刚度试验结果,评析了轻骨料混凝土规范JGJ 12—2006中轻骨料混凝土梁短期刚度的计算方法。另一方面,对非预应力混凝土梁与预应力混凝土梁,美国ACI 318-19[6]、欧洲EN 1992-1-1: 2004[7]及我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[8]等规范均采用了统一的短期刚度计算公式。而我国的轻骨料混凝土规范JGJ 12—2006与《混凝土结构设计规范》(GB 50010—2010)(2016年版)[9](简称混凝土规范GB 50010—2010)均采用刚度解析法构建非预应力混凝土梁短期刚度计算公式,采用双折线法构建预应力混凝土梁短期刚度计算公式,该做法形成了规范在理论上的缺陷[10]。非预应力混凝土梁与预应力混凝土梁在变形性能及机理上是相近的,故其刚度计算模式也应是统一的[11]。由于非预应力梁可视为预应力梁的特例,构建预应力混凝土梁短期刚度公式的双折线法同样应适用于非预应力混凝土梁。本文结合轻骨料混凝土试件开裂后弯矩-曲率曲线形状呈微凹的特点,给出了修正后的双折线计算模式,基于该计算模式构建了与预应力混凝土梁刚度公式统一的计算公式,并利用本文及收集到的试验数据对该计算公式进行了评析。
1 试验概况
1.1 试件设计
试验中设计了14根简支梁,包括10根轻骨料混凝土梁和4根普通混凝土梁。试件的主要参数见表1,试件的构造见图1。
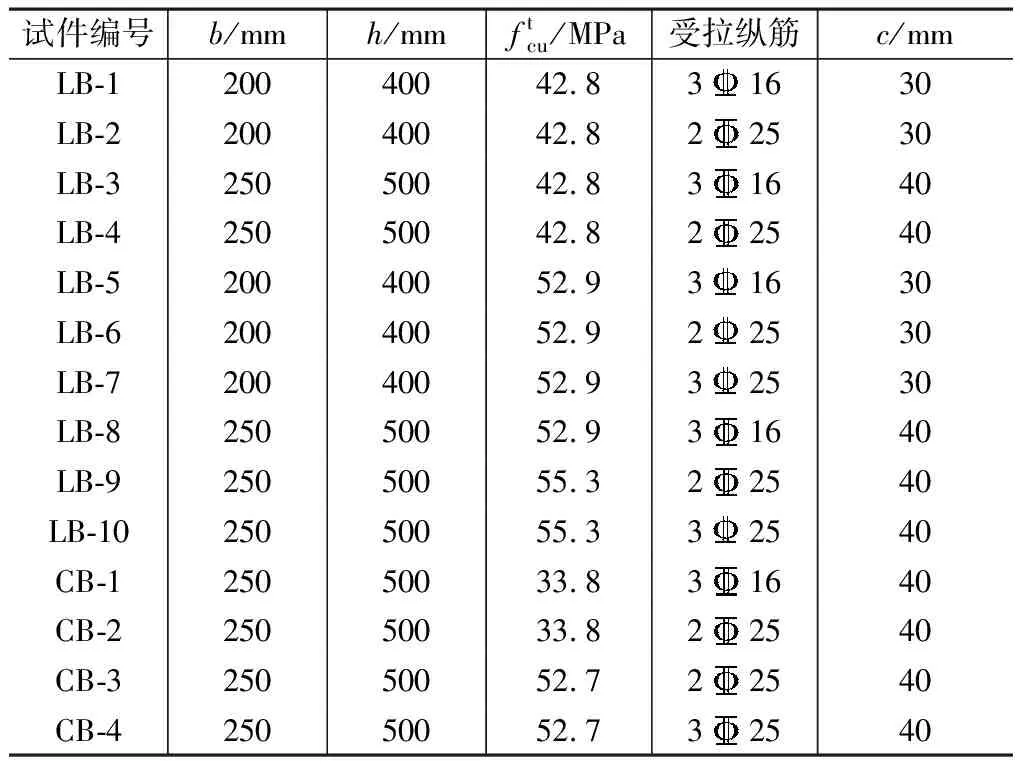
试件的主要参数 表1
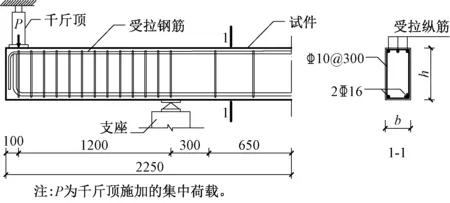
图1 试件构造图
1.2 材料及其性能
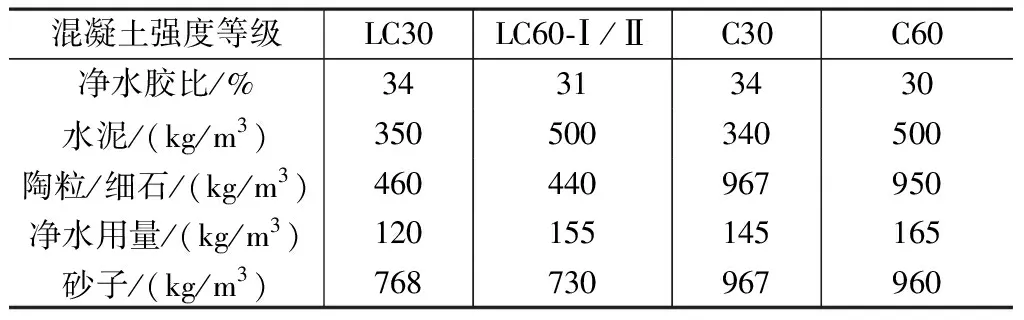
混凝土配合比 表2
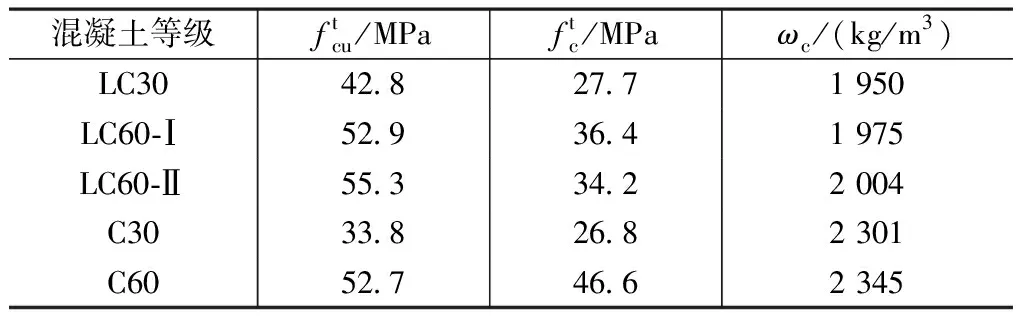
混凝土材性参数实测结果 表3
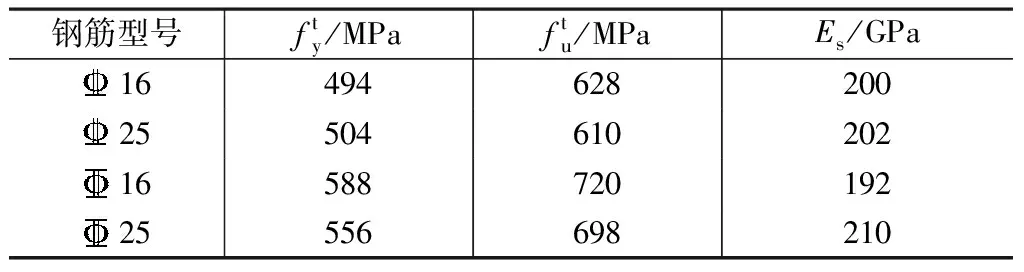
钢筋材性参数实测结果 表4
1.3 加载方式和测量方案
试验时为了方便观察试件跨中裂缝开展情况,采用反向加载方式加载,如图2所示,其中试件的悬臂段长度为1 200mm,纯弯段长度为1 900mm[12]。
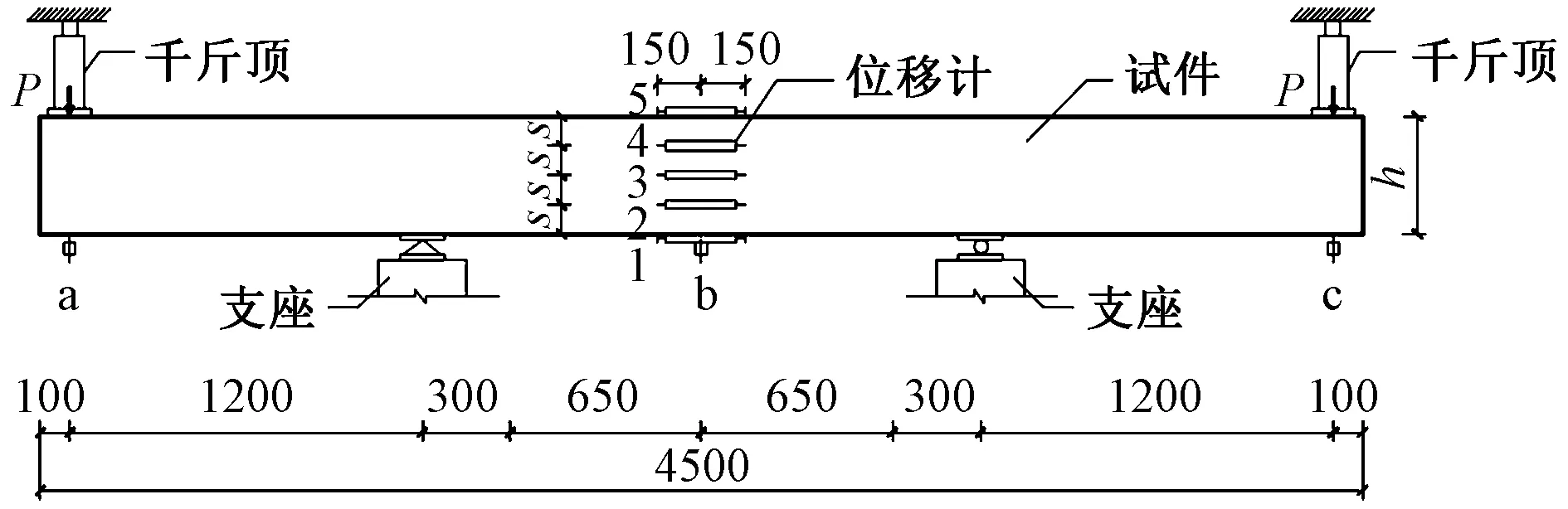
图2 试验加载位置及位移测点布置示意图
试验根据《混凝土结构试验方法标准》(GB/T 50152—2012)的规定进行加载,两端千斤顶同步加载。在荷载达到0.8Puc(Puc为根据跨中正截面受弯承载力确定的极限荷载值)前,采用力控制加载,每级加载增量为0.1Puc;之后,采用跨中挠度控制加载直至试件破坏,每级挠度加载增量为5mm。
如图2所示,在支座和跨中位置处布置位移计,可得试件的实测跨中挠度ft=fb-(fa+fc)/2。其中,fa,fb,fc分别为试件a,b,c位置处对应的实测竖向位移值(图2)。在试件跨中位置,均匀布置了5个水平标距为300mm的水平位移计,用以量测梁侧面混凝土平均应变,其中相邻两个位移计的竖向间距均为s,s取为h/4。
2 试验结果
2.1 试件跨中挠度
当荷载增加到约0.2Puc时,在试件纯弯段的底面、侧面出现宽度较小的裂缝。当荷载增加到约0.5Puc时,主裂缝基本出齐。进一步加载后,在主裂缝间距之间出现次生裂缝,但其发展高度和宽度均较小。当荷载增加到0.8Puc左右时,纵向钢筋进入屈服阶段,跨中挠度迅速增加。当荷载接近Puc时,裂缝不断向受压区延伸并变宽,此时受拉钢筋已进入屈服状态。当荷载达到Pu时,纯弯段部分裂缝迅速变宽,受压区混凝土被严重压碎。
各试件荷载-跨中挠度全过程曲线如图3所示。由图3可知,试件的荷载-跨中挠度曲线均呈典型的适筋受弯梁破坏的三阶段模式:1)试件未开裂前,梁可视为线弹性变化,其跨中挠度呈线性增加;2)当荷载达到开裂弯矩Mcr,裂缝的出现使得试件刚度降低,随着荷载进一步增加,挠度变化较为稳定,仍呈近似线性增加趋势;3)随着荷载进一步增加,梁中纵向受力钢筋屈服,试件跨中挠度突增,曲线斜率变化较大,试件刚度降低明显。此外,通过对比试件LB-5和LB-6、试件LB-8和试件LB-9可见,随着配筋率的提高,相同荷载作用下轻骨料混凝土梁的挠度明显减小。
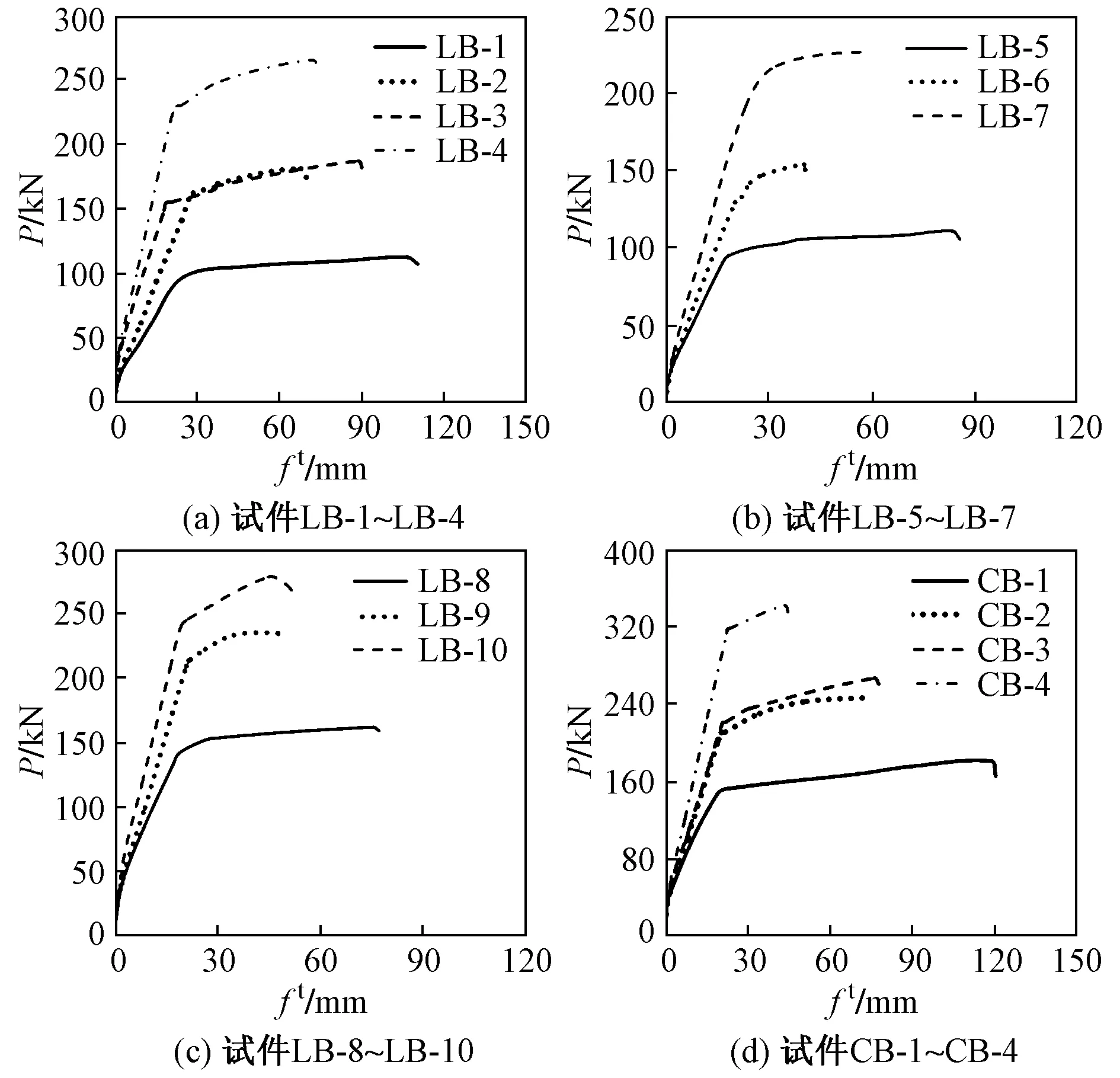
图3 荷载-跨中挠度全过程曲线
2.2 试件侧面平均应变
部分试件在不同弯矩下的纯弯段侧面沿截面高度的平均应变分布如图4所示。由图4可知,试件纯弯段侧面的混凝土平均应变沿截面高度大致呈线性分布。
不失一般性,假设最后一个资源余额的分配部门仅在{1,2}中选择且ni-≤n≤ni+,i=1,2.则应该将余额分给部门i=1,如果
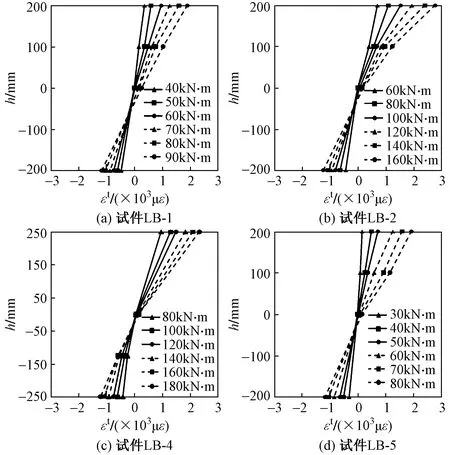
图4 纯弯段侧面沿截面高度的平均应变分布
2.3 试件边缘平均应变
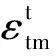
图5 纵筋屈服前试件纯弯段混凝土边缘平均应变
2.4 试件纯弯段平均曲率
试件跨中截面平均曲率φt可按式(1)计算:
(1)
由式(1)可得到纵筋屈服前试件的跨中弯矩-平均曲率曲线,如图6所示。
由图6可知:1)试件的跨中弯矩-平均曲率曲线在纵筋屈服前先近似呈直线,试件开裂后呈微凹曲线;2)对比试件CB-2和试件LB-4可见,由于轻骨料混凝土的弹性模量要比普通混凝土低,轻骨料混凝土梁刚度与普通混凝土梁相比较小;3)对比试件LB-5和试件LB-6可见,随着配筋率的提高,轻骨料混凝土梁的开裂弯矩变化不大,刚度明显增加;4)对比试件LB-3和试件LB-8、试件LB-4和试件LB-9可见,随着混凝土强度的降低,轻骨料混凝土梁的开裂弯矩和刚度均变化不大,但开裂后跨中弯矩-平均曲率曲线下凹更加明显。
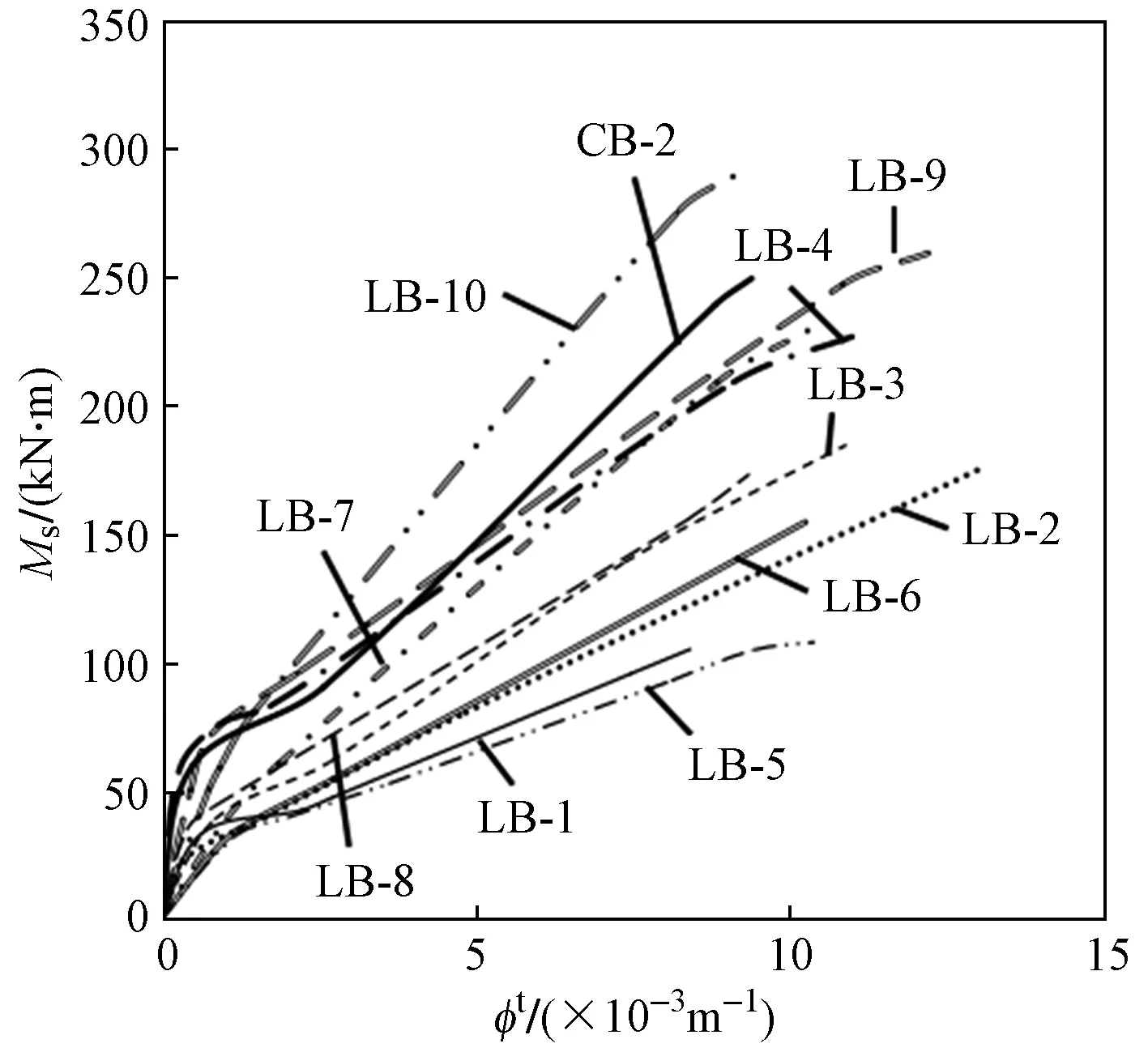
图6 纵筋屈服前试件的跨中弯矩-平均曲率曲线
2.5 试件刚度
(2)
根据式(2),可求得本次轻骨料混凝土试件的刚度试验值。根据混凝土规范GB 50010—2010,对非预应力混凝土构件的受弯短期刚度采用荷载效应准永久组合确定。但荷载效应准永久组合值和荷载效应基本组合值之比并不是一个定值,令按恒载标准值计算的弯矩为MGk,按活载标准值计算的弯矩为MQk,则弯矩准永久组合值为Mq=MGk+ψQMQk,弯矩的基本组合值为Md=γGMGk+γQMQk。其中,ψQ,γG,γQ分别为可变荷载的准永久值系数、永久荷载的基本组合分项系数、可变荷载的基本组合分项系数。可根据试件配筋、混凝土强度和截面尺寸等计算得到其极限受弯承载力Mu。令α=MQk/MGk,β=Mq/Md,Md=Mu,ψQ=0.4,γG=1.3,γQ=1.5,则有:
(3)
式中:α为按活载标准值计算的弯矩与按恒载标准值计算的弯矩之比;β为弯矩准永久组合值与弯矩基本组合值之比。
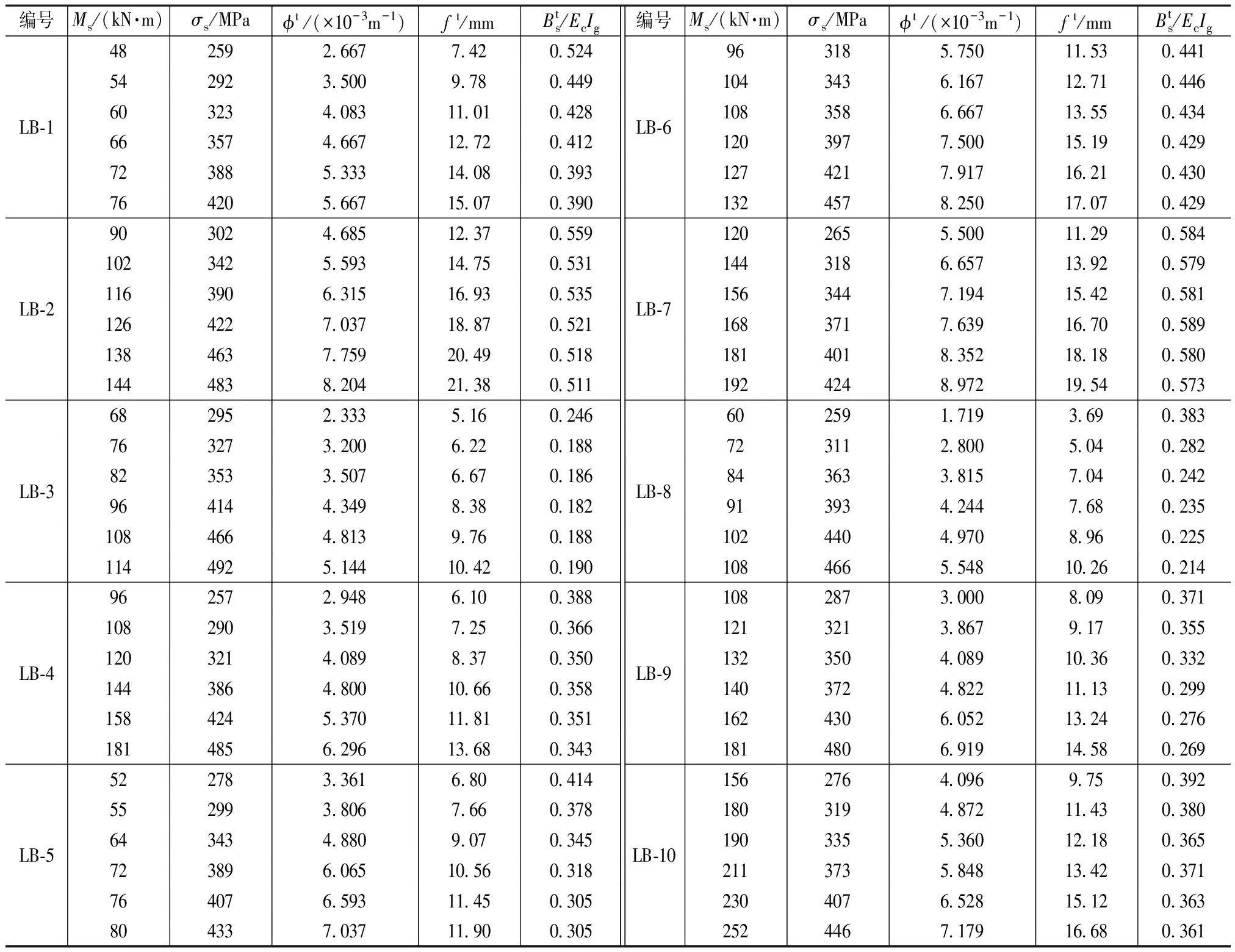
本文试件刚度试验结果 表5
2.6 相关文献中的试件刚度试验结果对比
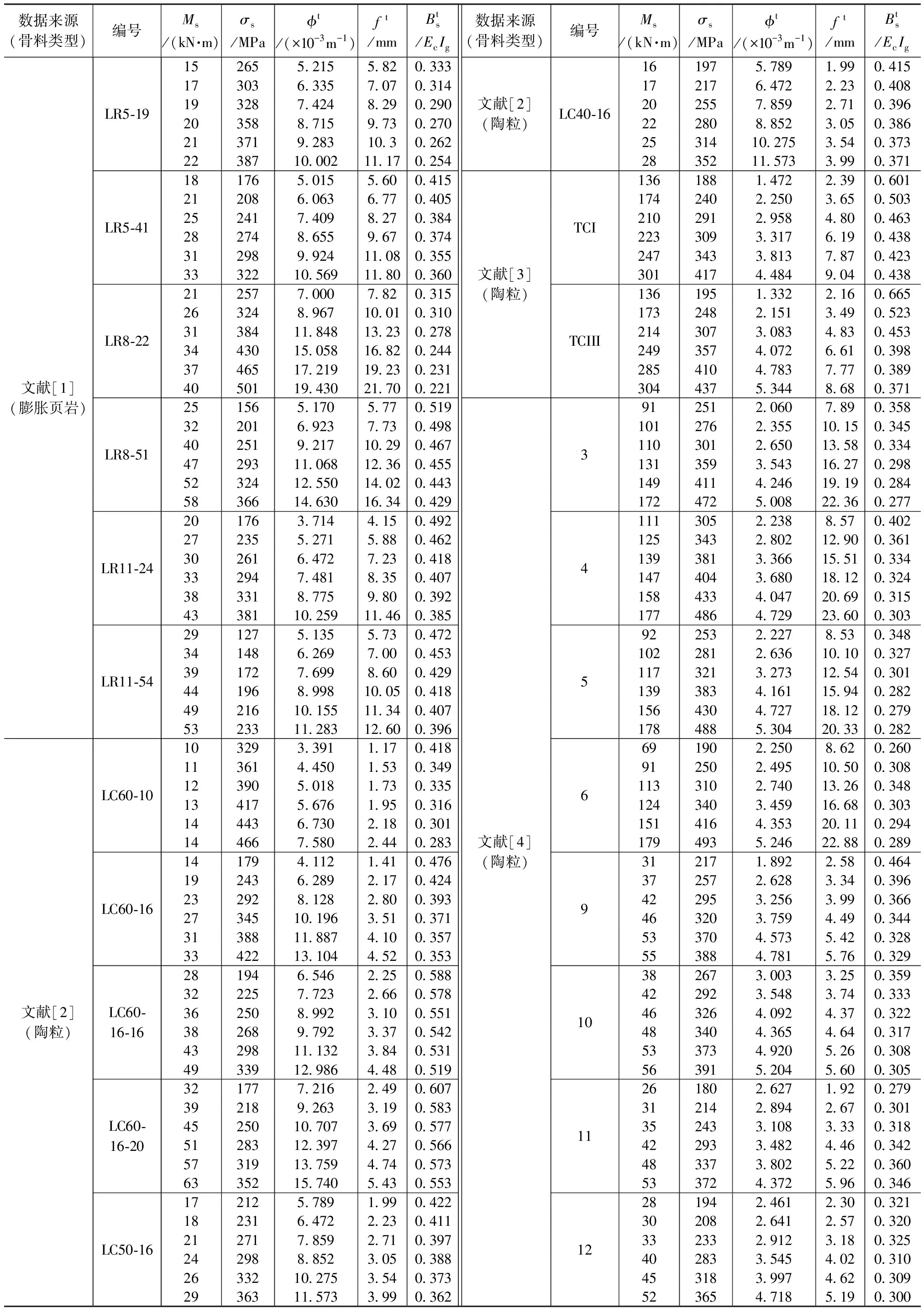
相关文献中的试件刚度试验结果 表6
此外,收集了相关文献中的22根高强钢筋轻骨料混凝土梁的短期刚度试验结果,试件的主要参数见文献[1-4]。对收集的试验结果进行处理后,每个试件取在荷载为0.3Mu~0.8Mu范围内6个受力工况,获得了钢筋应力σs为127~493MPa范围内的132组短期刚度数据,如表6所示。
其中,所有试件的钢筋弹性模量Es均取为200GPa;除文献[1]中试件的粗骨料为膨胀页岩,其他试件的粗骨料均为陶粒。结合本文的试验结果,共获得192组数据,可对高强轻骨料混凝土梁的短期刚度计算方法进行研究。
3 短期受弯刚度计算方法
3.1 基于刚度解析法的计算公式
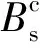
(4)
式中:As为受拉纵筋截面面积;h0为截面有效高度;ψ为裂缝间受拉纵筋应变不均匀系数;αE为钢筋和混凝土弹性模量的比值;ρ为纵向钢筋配筋率;γ′f为受压翼缘截面面积与腹板有效截面面积的比值;k1,k2,k3,k4均为根据试验确定的参数[13]。
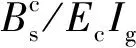

规范公式参数取值及计算结果 表7
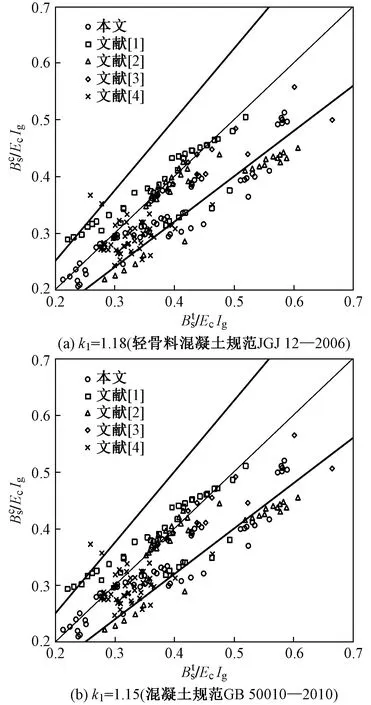
图7 短期受弯刚度试验值与计算值的比较
可根据最小刚度原则,按结构力学方法计算钢筋混凝土受弯构件的挠度[14]。分别按k1=1.18和k1=1.15计算的跨中挠度计算值f与试验值ft对比如图8所示。由图8可知,跨中挠度计算值和试验值均吻合较好,k1=1.18时跨中挠度计算值与试验值之比平均值为1.21,变异系数为0.220;k1=1.15时跨中挠度计算值与试验值之比平均值为1.20,变异系数为0.219。
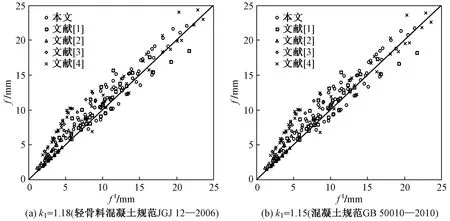
图8 跨中挠度计算值与试验值比较
3.2 基于弯矩-曲率曲线的计算公式修正
由图6可知,配置高强钢筋轻骨料混凝土梁在纵筋屈服前的跨中弯矩-平均曲率曲线分为两个阶段:1)构件开裂前,属弹性工作状态,关系曲线基本呈线性关系;2)构件开裂后,关系曲线呈微凹曲线或近似线性关系,其倾斜度小于第1阶段,且其倾斜度主要取决于纵向受拉钢筋配筋率的大小[13]。此外,试件开裂时,开裂截面处钢筋拉应力骤增,导致开裂截面附近一段长度钢筋粘结破坏,所以在第2段的开始点(即开裂弯矩处)出现了类似“屈服”的平台状态。由此,可以建立试件在纵筋屈服前的跨中弯矩-平均曲率关系模型,见图9。如图9所示,在平台状态后、纵筋屈服前的弯矩-平均曲率曲线在任意弯矩Ms作用下,梁正截面的曲率φs与开裂弯矩处曲率φcr、曲率增量Δφ存在以下关系:
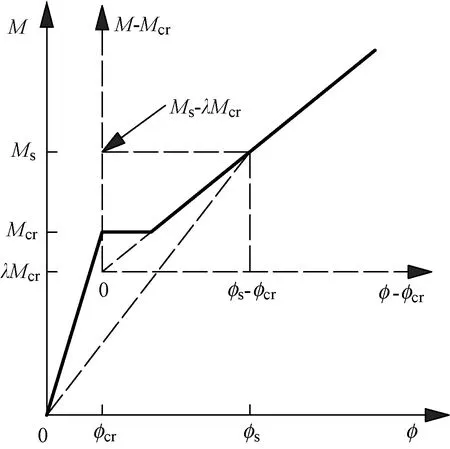
图9 跨中弯矩-平均曲率关系模型
φs=φcr+Δφ
(5)
令参数λ=M′cr/Mcr,则φs=Ms/Bs,φcr=Mcr/Bcr,Δφ=(Ms-λMcr)/ΔB。其中,Bcr为出现裂缝前正截面的弯曲刚度;令弯矩变化量ΔM=Ms-λMcr,则ΔB为ΔM对应的刚度变化量。代入式(5)中,并经处理后可得基于跨中弯矩-平均曲率曲线的配置高强钢筋轻骨料混凝土梁短期刚度公式:
(6)
其中,参数λ与曲线下凹程度有关。由前述建模关系可知,式(6)也应能适用于非预应力混凝土梁,且可克服规范刚度公式在开裂弯矩时的不连续性和计算偏差[15]。考虑到试验中第2段曲线下凹并不明显,仍可近似处理为线性关系。即将式(6)中λ取为1,则跨中弯矩-平均曲率关系曲线转变为双折线,如图10所示。此时,式(6)与轻骨料混凝土规范JGJ 12—2006和混凝土规范GB 50010—2010的预应力混凝土构件短期受弯刚度计算公式
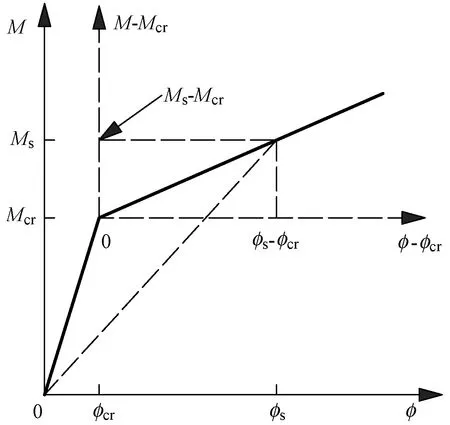
图10 跨中弯矩-平均曲率关系双折线模型
是一致的。
其中,根据轻骨料混凝土规范JGJ 12—2006 有:
Bcr=0.85EcI0
(7)
Mcr=γftkW0
(8)
式中:I0为换算截面惯性矩;γ为混凝土构件的截面抵抗矩塑性影响系数。
引入正截面抗裂系数Kcr和刚度比值系数ω,可得:
Kcr=Mcr/Ms
(9)
ω=Bcr/ΔB
(10)
则有:
(11)
根据试验结果,经参数回归分析,可得修正后的ω为:
(12)
式中γf为受拉翼缘截面面积与腹板有效截面面积的比值,相关部分系数按混凝土规范GB 50010—2010 确定。
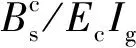
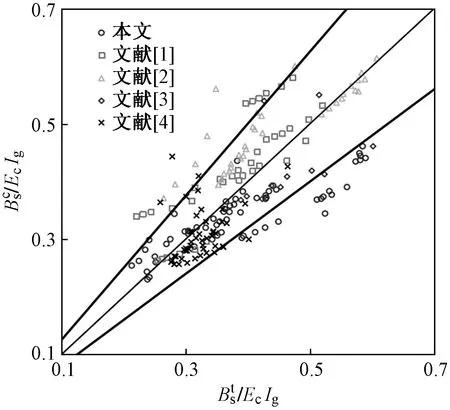
图11 短期受弯刚度试验值与计算值的比较
根据式(11)计算的短期刚度,基于最小刚度原则得到的跨中挠度计算值f与试验值ft对比如图12所示。由图12可知,跨中挠度计算值f和试验值ft吻合较好,二者之比的平均值为1.06,变异系数为0.250。
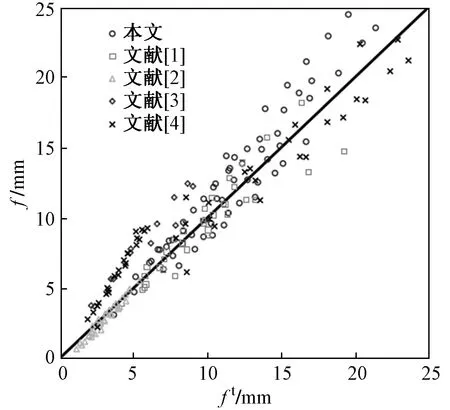
图12 跨中挠度试验值与计算值比较
4 结论
(1)对于配置高强钢筋的轻骨料混凝土梁,纵筋屈服前的跨中弯矩-平均曲率曲线在开裂后呈微凹曲线,且随着混凝土强度的降低下凹更加明显,部分试件在开裂弯矩处出现类似“屈服”的平台状态。
(2)与普通混凝土梁相比,轻骨料混凝土梁的短期受弯刚度较小;随着配筋率的提高,轻骨料混凝土梁的开裂弯矩变化不大,刚度明显增加。
(3)对于配置高强钢筋的轻骨料混凝土梁,受弯正截面符合平截面假定,按轻骨料混凝土规范JGJ 12—2006和混凝土规范GB 50010—2010计算的短期刚度计算值与试验值相比均略小,Kf分别为0.918和0.932。
(4)基于跨中弯矩-平均曲率曲线构建了考虑平台段的一般计算模式,并对于其特例(双折线法)拟合了与预应力混凝土构件刚度公式统一的计算公式,所得短期刚度计算值与试验值吻合较好,Kf为1.011。
