基于邻域最优概率的GRAPES快速更新循环同化预报系统逐时降水订正方法

罗聪，时洋，吴乃庚，张华龙，黄晓莹，苏冉

（1.广东省气象台，广东广州510641；2. 广东省生态气象中心，广东广州510641；3.中国气象局广州热带海洋气象研究所/区域数值天气预报重点实验室，广东广州510641；4.广州市气象台，广东广州511430)

1 引 言

数字网格预报是现代天气预报的核心业务，为精细的气象服务提供了高时空分辨率的预报产品支撑。随着人们对灾害性天气预报服务需求不断增加，逐小时、对流尺度天气预报的重要性日益凸显，为了进一步提升时空无缝隙的网格降水预报能力，高分辨率数值模式的解释应用是关键。童文雪等[1]针对对流降水预报发展了1 h更新循环的分步同化方案，有效提升了模式在12 h 时效内的降水预报能力；陈子通等[2-3]持续优化热带区域数值天气预报模式，进一步提升了强天气过程预报能力和气象要素预报精度。然而，由于中小尺度对流天气系统的时空尺度小，其动力和物理过程也尚未被完全认识清楚，模式对降水预报的时空不确定性可能导致高空报率和低命中率[4]。

气象学者发展了一系列基于数值预报的客观释用方法。这些方法总体上可分两类，一类是直接针对定量降水进行统计订正，例如，李俊等[5]应用频率匹配法对集合降水预报进行订正，改善了强降水预报效果；代刊等[6]总结了最优百分位、概率匹配平均等系列集合定量降水释用方法在业务中的应用；智协飞等[7-8]开展基于频率匹配的降水多模式预报订正，在减小降水量预报误差的同时，也提升了降雨雨区面积预报与实况的吻合度。另一类则是将定量降水预报转换为概率预报，以应对模式降水预报的时空不确定性，例如，Theis 等[9]采用邻域概率法的思路，利用邻域格点的定量预报计算得到中心格点的概率预报；潘柳杰等[10]利用邻域法评估了ECMWF、JMA 和T639 三家模式在不同空间尺度上的预报能力；马申佳等[11]同样利用邻域法检验了对流尺度集合预报在降水预报上的时空不确定性，并得到与其时空尺度相匹配的降水概率预报结果，提高了对流降水预报的技巧；刘雪晴等[12]开展了降水邻域集合概率的尺度敏感性试验，指出恰当的邻域概率半径可以得到更合理的降水概率预报；牛若芸[13]则提出了基于最优概率的降水量分级订正预报方法，实现概率预报和降水量级预报的融合。

总体而言，以往研究大多围绕集合预报开展日累积降水释用和评估，对快速更新的高分辨率模式的降水订正研究和业务应用并不多见。本文在前人研究工作的基础上，针对华南区域GRAPES 快速更新循环同化预报系统（GRAPES_GZ_R 3 km）降水预报的时空不确定性，采用邻域降水概率的思路，通过引入空间邻域、时间滞后因子进行了GRAPES_GZ_R 3 km 预报产品订正参数的确定，提出基于邻域最优概率阈值的逐时降雨分级订正方法，并进行检验评估，旨在提高区域快速同化更新模式对降水的预报可参考性。

2 资料和方法

2.1 资料介绍

（1）华南区域GRAPES 快速更新循环同化预报模式资料。逐小时循环同化更新的24小时逐时降水预报（其中2019 年8 月起预报时效延长至30小时），空间分辨率为3 km，资料时长为2019—2020年，每年的4月1日—9月30日。

（2）实况资料。2019—2020 年，每年的4 月1日—9月30日，包括广东省86个国家级自动气象站和约3 000个区域自动气象站的逐小时降水数据。

强降水是预报业务中的关注重点，因此本文选取2019年汛期（4—9月）广东区域性暴雨过程[14]的资料用于建模训练。利用空间邻域概率和时间滞后集合的方法，将邻域格点的确定性预报转变为中心格点的概率预报，并基于历史训练期的分级降水最优概率实现定量降水订正预报，选取2020年4—9月的资料用于检验。

2.2 邻域法

由于中小尺度对流性降水具有明显的空间分布非均匀性，高分辨率数值模式的降水预报通常也会出现较大的预报偏差，以往研究表明，邻域法在订正预报空间误差上是一种较为有效的方法，因此，引入该方法对GRAPES_GZ_R 模式预报结果进行后处理，综合格点邻域范围内的降水值，进而得到更优化的降水预报结果。

首先，将小时雨量分为4 个等级，其取值记为Gk(k=1，2，3，4)，依次对应0.1 mm、2 mm、10 mm、20 mm。

其次，对模式的降水场进行“0/1”二分类处理，即超过降水阈值Gk的格点记为1，反之为0，从而得到降水阈值Gk对应的二进制降水概率场BP(i，j)，选择适当的邻域范围对概率场BP(i，j)进行平均，即可得到中心格点的邻域概率：

式中，i为经向格点，j为纬向格点，n为邻域范围内格点数，P(i，j)为Gk对应的邻域概率场。

2.3 邻域窗选取

不难看出，邻域窗大小的选择将直接影响邻域法得到的邻域概率场的分布，即在多大空间尺度上模式预报性能最优，这是模式应用的关键问题。以往学者对邻域窗的选择通常采用圆形或正方形两种类型，但Ebert[15]的研究表明，邻域窗的形状对邻域概率的结果没有明显影响。考虑到方形的邻域窗可以和数值模式的经纬格点相匹配，且计算相对简便，因此，本文选择正方形邻域窗来计算降水的邻域概率。

为了确定最优的邻域窗大小，需对不同邻域半径的邻域概率进行检验。对于二分类事件的概率预报检验，存在很多标量准确性的量度标准，Brier 评分（BS）就是其中一种。BS 评分本质上是概率预报的均方误差，且是一个负向评分，结果越接近0越好。BS及其斜率的计算公式如下:

式中，Pk为预报概率；Ok为实况概率，当实况事件发生则观测为1，不发生则为0；rd为不同的领域半径，SLP为BS随邻域半径变化的斜率。

图1为不同等级降水的BS评分随邻域半径的变化。以小时雨量超过20 mm、6 h 预报时效为例（图1a），邻域半径为3 km 的BS评分为0.021 3，而邻域半径为60 km 的BS 评分快速下降至0.009 3，但随着邻域半径继续增加，BS 评分下降幅度已经十分微弱，邻域半径为150 km 的BS 评分为0.007 9，仅仅比邻域半径为60 km 时下降了0.001 4，BS 斜率接近于0。对于10 mm、2 mm 和0.1 mm 以上的小时雨量，邻域半径分别在90 km、120 km、150 km 处，BS 斜率接近于 0，但当邻域半径达到60 km 时，各个等级降水的BS 下降均已成明显变缓的趋势，其余时效也表现出类似的变化趋势。因此，综合考虑BS 评分和计算效率，在实际业务中把60 km 作为邻域窗半径是较优的选择。

图1 降水超过0.1（a）、2（b）、10（c）、20（d）mm/h的邻域概率BS评分随邻域半径的演变

为了进一步考虑模式不同时间起报的不确定性，引入时间滞后因子，以t0为当前起报时刻，选取t0-H～t0时刻内所有时次起报的模式预报场数据，分析不同时间滞后参数H对应的邻域概率变化，以确定合理的时间滞后窗。

由于2019 年的GRAPES_GZ_R 模式预报时效仅为24 h，因此，图2 仅给出了6 h、12 h、18 h 对应的邻域概率BS 评分随时间滞后的演变。以小时雨量超过20 mm、6 h 预报时效为例（图2a），对比未考虑时间滞后（0 h）与时间滞后4 h 的邻域概率场，BS 评分从 0.009 3 下降至 0.008 0，下降幅度为14.4%，但当滞后窗从4 h增加到5 h时，BS评分仅下降1.3%；随着预报时效增加，BS 随时间滞后窗扩展而下降的趋势更加缓慢，在实际业务中将时间滞后窗定为4 h是较合理的选择。

图2 降水超过0.1（a）、2（b）、10（c）、20（d）mm/h的邻域概率BS评分随时间滞后的演变

2.4 邻域最优概率法

邻域法提供的是降水概率预报场，为了得到确定性降水订正场，采用基于邻域最优概率阈值的降雨分级订正方法，将降水量概率预报转换为定量降水预报，具体步骤如下。

（1）利用2019 年4—9 月的资料用于建模，训练所有气象站点在不同降水等级Gk对应的邻域概率Pk。

（2）从0～1每隔0.01设定一个概率阈值Pj，计算降水等级Gk在每个概率阈值下的TS评分TSkj。

（3）提取TSkj中最大值对应的概率阈值Pj（Max），作为降水等级Gk的最优概率阈值OPk。

（4）对于任意格点，计算实时预报的邻域概率场，由高到低逐级比较该点各预报等级的Pk和OPk，若Pk≥OPk，则停止判别，并赋值Gk为该点的逐时降水预报等级值，记为PGk；然后选取其邻域范围内的格点降雨预报结果fk，以及降水等级同为PGk的格点概率Pk，利用式（6）计算基于最优概率的定量降水F(i，j)，订正流程见图3。

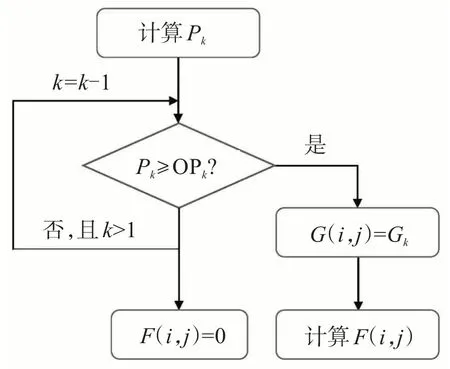
图3 逐时降水订正流程图

利用2019年的区域性暴雨过程资料统计分析（图4，见下页），以12 h预报时效为例，对于20 mm以上的小时雨量，最优邻域概率为10%，TS评分达到0.034，随着概率阈值的增加，TS 评分迅速降低（图4a），10 mm、2 mm 以上降水以及晴雨预报的最优邻域概率阈值分别为15%、25%和65%，相应的 TS 评分为 0.058、0.170 和 0.747。总体而言，降雨越强，对应的最优邻域概率阈值越小。

图4 12 h时效的不同邻域概率下逐时降水TS评分

3 检验与分析

为了评估基于邻域最优概率的逐时降水订正效果，本研究对2020年4月1日—9月30日的所有逐时起报时次的模型订正结果进行检验，主要检验对象为晴雨准确率、强降水准确率和偏差（BIAS）。特别注意的是，2020 年 3 月 1 日起，GRAPES_GZ_R 的预报时效从24 h 延长至30 h，但由于无法利用2019 年的历史数据对30 h 预报时效进行建模，因此只能将24 h 预报时效的参数应用于2020年的30 h预报时效。结果分析如下。

3.1 晴雨预报检验

本方法采用的晴雨预报TS（TS_s）计算公式如下：

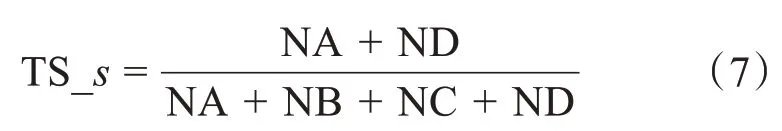
式中，NA 为有降水预报正确站（次）数，NB 为空报站（次）数、NC为漏报站（次）数，ND 为无降水预报正确的站（次）数。

图5给出的是2020年汛期（4—9月）晴雨预报检验。GRAPES_GZ_R 的晴雨预报TS 并非简单地随预报时效增加而下降，而是呈现先降后升的变化：1 h 的TS 评分最高，达到0.900，1~6 h 内 TS呈下降趋势，6 h的TS为0.823，在6~12 h内TS逐渐上升，12 h的TS达到0.853，随后TS维持相对稳定，介于0.85～0.86之间。

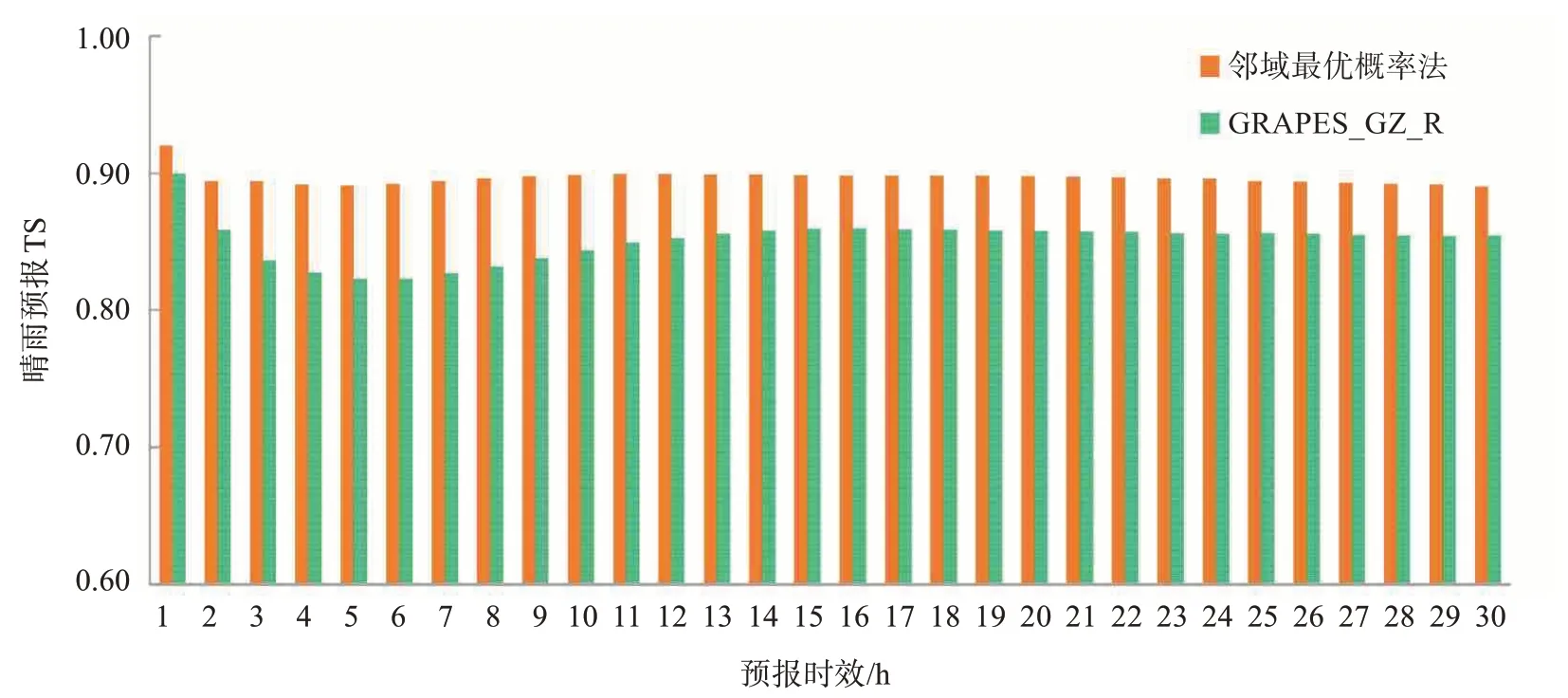
图5 2020年汛期的晴雨预报检验

经过邻域最优概率订正的晴雨TS 在1 h 预报时效达到 0.920，2~30 h 的 TS 维持在 0.89～0.90 之间，基本不随预报时效增加而降低。与原始的GRAPES_GZ_R 模式预报相比，邻域最优概率订正后的晴雨预报全部为正技巧，其中1 h 提升了2.2%，6 h 提升了8.4%，总体提升了约5.3%。上述结果表明，邻域最优概率法可以提升逐时降水的晴雨预报准确率，且订正后的预报效果更为稳定。

3.2 强降水预报检验

本研究定义的强降水标准为小时雨量超过20 mm，采用的检验标准包括强降水预报TS（TS_r，式（8））和预报偏差BIAS（式（9）），计算公式如下：

其中，NA 为强降水预报正确站（次）数，NB 为空报站（次）数，NC为漏报站（次）数。

图6给出的是2020年汛期4—9月强降水预报检验。GRAPES_GZ_R 的强降水预报TS 随时效有较明显的变化：最高出现在2 h 时效，达到0.016，而3~6 h 的强降水TS 同样处于较低水平，约0.007～0.009，与晴雨预报类似，其余时次强降水预报TS 介于0.008～0.012 之间，所有时效的强降水预报TS 平均约为0.01。经过邻域最优概率订正后，强降水预报TS 均表现为正技巧，TS 较低的时次出现在 3~6 h 时效，从 6 h 时效起，TS 逐渐升高，12 h 时效的TS 最高达到0.022，随后又逐渐降低，所有时效的TS 平均约0.014，高于原始模式预报。

图6 2020年汛期的强降水预报检验

预报偏差BIAS 是天气事件的预报次数与实际发生次数的比率，理想状况为1，而BIAS＞1表示预报高于实况频率，BIAS＜1则相反。然而在实际业务中，尤其是在面对可能致灾的天气时，由于存在空报和漏报的情况，TS 和BIAS 通常不能同时达到最优，BIAS=1 也未必是最优选择。GRAPES_GZ_R 模式在 1 h 时效的 BIAS 为 0.758，也反映开始阶段模式的强降水预报偏弱，2~5 h 时效 BIAS 突增至4 左右，空报明显增多，6 h 开始逐渐降低，12 h 后维持在1 左右，空报和漏报基本相当。订正后，1~4 h 时效的BIAS 普遍高于模式预报，5 h 起 BIAS 逐渐降低，12 h 后同样维持在 1 左右，与模式大致持平。

综合强降水TS 和BIAS 表现可知，模式对强降水的预报能力并非单纯随预报时效增加而下降，而是在3~6 h 通常表现有所下降，6 h 后逐渐上升，在12 h前后表现较优，随后又逐渐下降。订正后的预报也表现出类似的变化特征，12 h 前后的订正效果最为明显。从BIAS 分析表明，对于模式前期预报能力较弱的时次，本方法主要是以更多的空报为代价来提升预报评分，后续可以考虑结合其他算法进行消空订正以进一步提高TS 评分；而本方法对于模式12 h预报时效后的订正，在空报和漏报上达到较好的平衡，BIAS接近1。

3.3 个例应用分析

锋面降水个例：2020 年 5 月 20 日下午到 22 日中午（北京时间，下同），广东出现年内第一场“龙舟水”（每年5 月21 日—6 月20 日）强降水，其中21日夜间至22日早晨，受强雷雨云团影响，珠江三角洲出现大范围的强降水，广州黄埔区录得最大1 h雨量167.8 mm，东莞东城区录得最大3 h 雨量351 mm，均突破广东“龙舟水”期间历史极值。

5 月21 日20 时起，粤北的韶关和河源的南部有雷雨云团逐渐发展，并缓慢向西南方向移动，23时前后，云团移动至珠江三角洲的广州和惠州一带，强度不断增强，同时移速变慢，在当地形成持续性强降水。以降水最为强烈的22 日03 时为例：21 日 14 时（ 北 京 时 间 ，下 同 ）起 报 的GRAPES_GZ_R模式第13 h时效（图7b）尽管预报了22 日03 时广州有强降水，但是范围明显偏小，位置偏西；进一步分析更早的模式预报（图7c~7f）发现，10~13时起报的GRAPES_GZ_R模式普遍预测22 日03 时珠江三角洲地区将有强降水，但不同时次起报的位置和强度、范围均有不同的偏差，表明模式预报的时空不确定性较大。采用空间邻域和时间滞后订正后的概率产品较准确地预报了广州、东莞一带为高概率的强降水中心（图7g），并超过历史统计的强降水最优概率阈值（10%），表明该地区出现强降水可能性很大。订正后的定量降水预报中心的时雨量超过50 mm（图7h），尽管极值中心与实况仍有一定偏差。然而，由于模式多个时次均在粤东沿海预报有强降水，订正后的结果也在该地区出现了空报，这也是本方法仅对降水采取时滞集成订正存在的不足，后续或可加入风场等要素进行协同判断以提升订正效果。总体而言，订正后的强降水落区和范围与实况较为吻合，强降水TS 达到0.271，明显高于同时次模式的强降水TS（0.155），也体现了本订正方法对于具备一定范围的锋面降水订正能力较好。

图7 2020年5月22日03时降水实况(a)，GRAPES_GZ_R模式不同时次起报的降水(b~f)，领域概率法2020年5月21日14时起报的强降水概率（g）和小时降水量（h）

暖区降水个例：2020年6月5—9日，广东出现了一次典型的暖区降水过程，其中6 月7 日凌晨起，受西南季风影响，珠江口东侧沿海地区出现强降水云团并不断发展，缓慢向东北方向移动，造成持续性强降水。

以7 日06 时为例：强降水主要位于广东南部的汕尾和惠州、肇庆北部（图8a），6 日20 时起报的GRAPES_GZ_R 模式10 h 时效（图8b）对汕尾、惠州中部的强降水预报明显偏弱，同时在广州、韶关和河源交界地区出现了明显的强降水空报，分析更早的16—19时起报的模式预报（图8c~8f）发现，GRAPES_GZ_R 模式大部分预报了汕尾地区的强降水，但普遍没有预报广州、韶关和河源交界地区的强降水，同样也漏报了惠州中部的强降水。经过空间邻域和时间滞后订正后的概率产品保留了汕尾的强降水中心预报（图8g），并扩大了20 mm以上的降水预报范围（图8h），同时也对广东中东部的强降水空报有一定的抑制作用。订正后的强降水TS 达到0.164，高于同时次的模式强降水TS（0.058）。因此，对于一些模式能较稳定预测的暖区降水个例，基于时滞集成的概率和定量订正预报也能提供一定的分析参考，可作为快速循环同化模式业务应用的支撑技术。

图8 2020年6月7日06时降水实况(a)，GRAPES_GZ_R模式不同时次起报的降水(b~f)，领域概率法6日20时起报的强降水概率（g）和小时降水量（h）

4 小结与讨论

高分辨率数值预报的时空不确定性问题已经得到广泛的关注，本文利用邻域最优概率方法对华南区域GRAPES 快速更新循环同化预报模式进行逐时降水订正，提升了模式的晴雨和强降水客观预报能力。

（1）采用邻域法对GRAPES_GZ_R 模式降水概率计算时，其最优邻域半径随降水等级增加而减小，晴雨预报的最优邻域半径可达150 km，而强降水的最优邻域半径为60 km。

（2）通过引入时间滞后因子能进一步改善模式不同时间起报的不确定性。BS 评分随着时间滞后窗的增加而进一步改善，但是预报时效越长，改善效果越不明显，结合BS 评分确定了时间滞后窗为4 h。

（3）利用邻域最优概率法对2020 年的GRAPES_GZ_R 模式预报进行订正，检验表明：晴雨预报和强降水预报均为正技巧。晴雨TS 评分达到0.89以上，与模式预报相比提升约5.3%，且预报效果更为稳定，基本不随预报时效增加而降低。强降水TS 评分呈先降后升趋势，在12 h 时效前后预报效果最优，TS 评分达到0.022，随后又逐渐降低，所有时效的TS 平均约0.014，高于原始模式预报。

综上可见，采用邻域最优概率法对提高GRAPES_GZ_R 模式预报性能具有较为明显的效果。不过，由于数据样本的限制，本文重点讨论了该方法对GRAPES_GZ_R 模式24 h 的改善效果，对于更长预报时效、以及该方法对其它业务数值模式的可适性还未进行分析。另外，尽管该方法能提高降水预报的TS 评分，但如何更好地消除空报和漏报仍然需要更多的后续研究。