异构融合网络下超采样图像细节增强仿真
2021-12-10邹小花
邹小花,夏 容
(南昌航空大学科技学院,江西 南昌 332020)
1 引言
图像在异构融合网络信息交互的情况下容易丢失一些细节,导致图像变得不完整、纹理不自然、边缘模糊,不能满足用户的需求。如何使图像细节在异构融合网络下得到增强,进而提高图像质量是在医学诊断、军事卫星以及高清晰视频领域等研究的重要课题,并具有极高的科学价值。
针对上述问题,相关人员对图像细节增强进行了研究,但是仍有许多不足。例如文献[1]提出基于非下采样轮廓小波变换的图像细节增强方法,使用频域分析算法对图像进行分解,得到图像的轮廓,从而获得图像的高频和低频信息,为了改善低频图像亮度不均匀等问题,再对低频图像做视网膜增强处理,同时对高频图像做非线性增强,通过去噪处理后得到高频特征图;在粗糙的低频图像范围内分析高频图像的显著性特征,最后将高频图像与低频图像进行融合得到精细的细节增强图。此方法能够最大化的利用高频与低频图像信息,并且可以控制光照对实验的影响。文献[2]为加强遥感图像的细节处理,将传统的非下采样法与模糊理论相结合,研究出一种遥感图像增强算法。首先将原始图像做NSCT变换处理,得到不同子带上的高频系数与低频系数,利用模糊理论对高频系数进行处理,并将这些系数设立成隶属度函数;再按照从高层到底层的顺序,将高频系数线性逐层加入到低频中,全部加入后,实现遥感图像细节的增强。该方法无论在主观还是客观方面都能增强遥感图像的细节。文献[3]提出一种基于图像跨尺度相似性和特征组合的图像超分辨率重建方法。首先利用图像的跨尺度相似性,采用KNN算法分别建立高、低分辨率图像之间的像素特征和梯度特征的映射关系,然后利用像素特征映射关系对输入图像重建包含高频信息的高分辨图像,利用奇异值阈值化获取输入图像的有效高频信息,并利用梯度特征映射关系将高频信息放大后分块叠加到高分辨率图像上,得到最终的图像重建结果。
上述方法虽然使图像的细节得到增强,但是在设计过程中未能考虑到图像的纹理方向,导致图像边缘不清晰,存在锯齿现象,并且需要改变的计算参数很多,实验操作起来比较复杂。针对以上问题在异构网络融合基础上,提出超采样图像细节增强研究。超采样图像技术可以有效的提升图像的细节质量,与其它增强图像细节的方法相比,该方法可以快速提高图像的分辨率、降低画面噪点,从而增强图片细节。
2 异构融合网络下超采样图像细节增强
2.1 异构融合网络下奇异值算法模型建立
异构融合网络[4]是指网关将各种类型的网络连接到核心网络中,最终融合成为一个整体,是时代发展与科技进步的必然趋势。网络融合有很多的优势,使网络的覆盖范围扩大,让网络资源得到高效利用,从而降低运营的成本;融合可以满足用户多样化的需求,为用户提供更好的服务。图1为网络异构融合示意图。
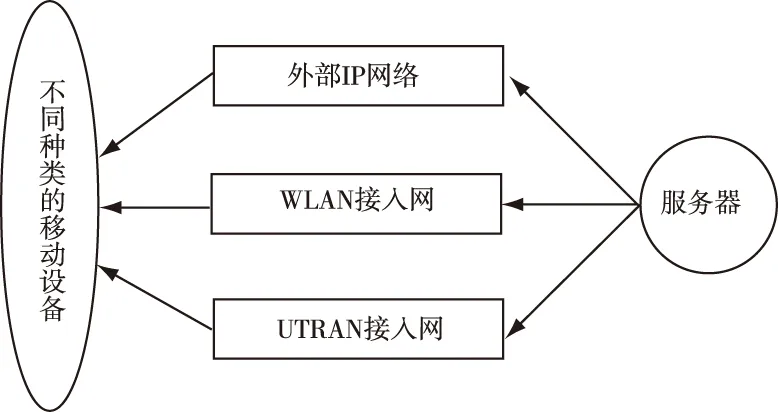
图1 异构融合网络示意图
要想在异构融合网络环境下增强超采样图像的细节,需设定一个低分辨率图像为L,再通过双三次差值方法[5]把该图像的边缘部分变得模糊,使它成为缺少细节且分辨率较高的低频图像,将H设定为目标图像,从而获得目标高频细节图像

(1)


标准的奇异值算法模型的建立是对M*N矩阵里的A进行分解,其步骤为:
步骤一:利用正交变换方式,对A矩阵进行消减,变换成双对角矩阵B
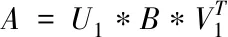
(2)

U1为M*M的正交阵;
B如果它满足M*N的上双对角矩阵,则M≥n;如果满足M*N的下双对角矩阵,则M 对矩阵B做奇异值分解,得出 (3) S为对角矩阵,其中每个元素分别对应一个奇异值。 将式(2)与式(3)相结合,就可以得到奇异值分解的公式为 (4) 在矩阵S中,任何一个元素σ都与矩阵A中的一个特征值相对应。根据降序储存的顺序σ≥σi+1(i≥0)假设U=U1*U2,这样矩阵A中的右奇异值全部储存在U中。相同道理可以得出矩阵A的左奇异值都储存在V中。因此在异构融合网络下矩阵A的奇异值算法模型为 (5) 此奇异值算法模型有两个重要的目标: 2)无论是低频图像块还是高频图像块所得到的稀疏表示系数均相同。 在异构融合网络环境下根据局部自适应性特点,搜索原始低分辨率图像,获取最准确的匹配块,利用奇异值算法模型对图像进行矩阵重构[7],获取有价值的高频细节信息。细节增强算法由4部分组成分别为: 1)初始差值:采用哪种方式的差值算法会影响最后的分辨率效果,差值算法较好得到的结果就越准确,本文在获得原始分辨率图像时使用的是轮廓模板差值法,该方法能够较好的保持原始图像的基本轮廓。 2)块匹配搜索[8]:找出两个图像块的对应点,并且计算出对应的像素之差,所得的值作为图像匹配的准则。Y0作为原始的高频图像,对此进行逐点分块处理,图像里全部像素点b∈Y0,得到的坐标是(bx,by),将b看作右下角的一个控制点,构建一个分辨率为i×i的图像参考块,示意图如图2所示。 图2 超采样图像参考块示意图 上图展示了其中一个块划分的图像,一个小方格对应一个像素点,图中粗线框架表示划分为4×4的块。 对初始低分辨率图像中控制点b上的对应像素ρ进行计算,坐标为(ρx,ρy),公式如下 ρx=bx/scale,ρy=by/scale (6) scale代表图像的缩放因子,将ρ设为搜索中心,构建5×5的搜素范围窗,并且在此范围窗内做完整的匹配搜素。将每个匹配块与目标参考块进行匹配值计算,匹配值最小的匹配块是参考块的最佳匹配。 奇异值分解算法分别为原始超分辨率图像与低分辨率图像提供目标块和学习块,在匹配过程中会用到很多的初始图像信息,这样会降低计算的复杂程度,计算起来较为简便。 3)奇异值阈值:将最佳匹配块R变为高频图像Rh的计算公式如下所示 Rh=R-R*Gσ (7) 高频图像Rh奇异值分解后得到Rh=U∑VT,获得如下所示的奇异值矩阵 ∑=diag(λ1,λ2…,λr),λ1≥λ2…λr≥0 (8) (9) 经过奇异值分解获得初始超采样图像目标块Bi(Bi⊂Y0)所对应的高频图像 (10) (11) (12) 将以上操作步骤反复进行,直到所有的图像块都完成上述操作,最终得到完整的超采样图像细节增强图。 异构融合网络下对超采样图像做细节增强时,图像的边缘或者细节较多的地方,由于叠加图像的高频图像中会有伪高频成份存在,此种伪高频可以看做是一种噪声,但并不是普通的高斯噪声、脉冲噪声等。可以利用奇异值分解算法对其进行去噪处理,不需要对噪声类型做假设,处理过程极其简单。 图3为所提方法操作流程。 图3 细节增强流程图 为了验证本文图像细节增强算法的有效性,将主观视觉与客观的峰值信噪比、结构相似度作为评价标准完成对比实验。将所提算法与文献[1]、文献[2]算法做对比分析。为了实验的公平性,在进行对比时,采用的参数需要一致,原子数量为800,稀疏度设为5,块的大小为5×5,重叠大小是5。 设置第一组为对物品图像细节的增强实验,图4为三种不同算法对图像细节增强的效果。 图4 实验一图像细节增强的效果图 峰值信噪比:常用作图像压缩等领域信号重建质量的测量,本文通过对比该值分析细节增强图像清晰度 (13) 式中,MAXI表示图像点颜色的最大数值,MSE表示图像均方差。两个m×n单色图像I和K的均方根误差为 (14) 下表为实验一得出的三种算法的峰值信噪比与结构相似度对比表: 结构相似度是对图像质量进行打分评价的一个很经典的指数,取值范围[0,1],值越大,表示图像失真越小。从第一组的对比实验中可以看出,本文使用方法得到的细节增强图像清晰度高,帽子的纹理较清晰,达到了有效增强效果,而文献方法得到图像存在非常明显的面块现象,细节信息丢失。 第二组实验设置为对动物皮毛图像细节的增强实验,以下三幅图为第二组实验得到的超采样图像细节增强图: 图5 皮毛图像细节增强的效果图 下表为实验二得出的图像对比结果: 经过对比可以看出采用本文算法进行细节增强的图像中,动物的皮毛纹理会比初始图像更加的清晰,文献[1]、文献[2]算法对图像中大面积的震荡纹理处理效果较差。 表1与表2在客观上对三种算法做出比较,从数据显示的信息可以看出,本文方法与文献[1]、文献[2]方法相比,会产生更高的峰值信噪比并且结构相似度接近于1。因此在异构融合网络下,使用本文算法对超采样图像细节的增强有较好效果。 表1 帽子图峰值信噪比与结构相似度对比表 表2 皮毛图像峰值信噪比与结构相似度对比表 本文提出了异构融合网络下超采样图像的细节增强。通过采集训练样本,建立奇异值算法模型,利用奇异值分解与阈值算法,获取最佳匹配图像,对该图像做加窗处理后使图像的细节部分得到增强。通过实验对比,无论是图片的直观感受,还是客观的峰值信噪比与结构相似度的数据,都表明本文方法不仅提高了奇异值算法的性能,而且实现图像细节增强的过程简单、快速,与其它方法相比能很好的实现图像的细节增强。




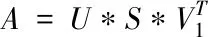
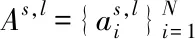
2.2 超采样图像细节的增强








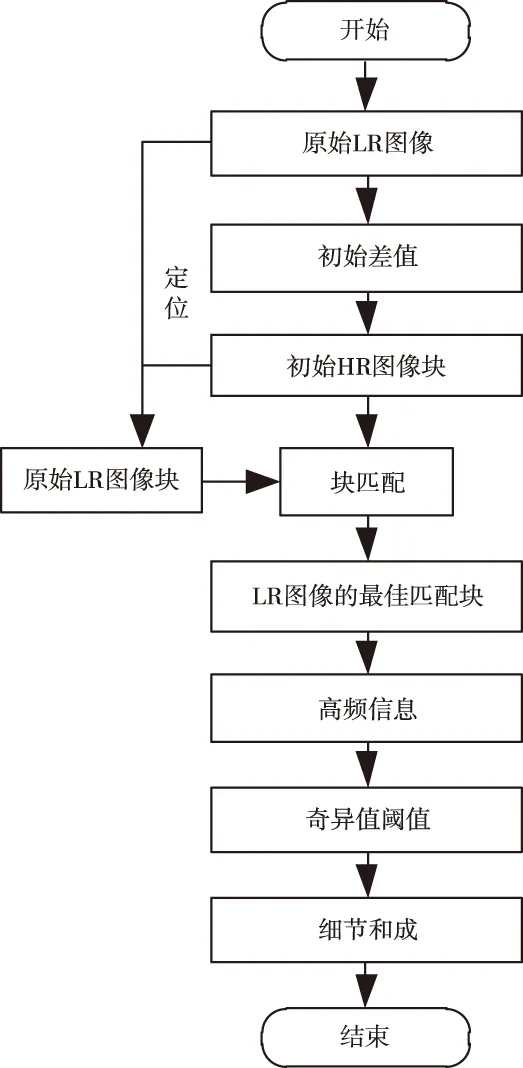
3 实验分析
3.1 实验参数
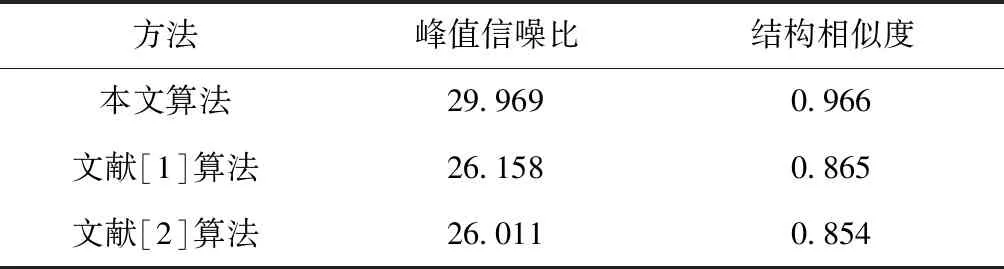
3.2 实验结果分析

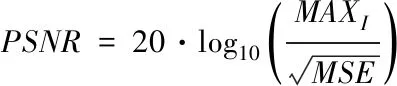



4 结论
