水电站引水系统流量-压力仿真

杨 军，赵小明，邬育仁，刘 名

(国能大渡河大岗山发电有限公司，四川雅安 625000)

1 引言

1.1 系统仿真简介

仿真的定义有不同的说法，而比较经典的定义即“所有支持模型建立与模型分析的活动即为仿真活动”。从定义可知“系统、模型、仿真”三者之间有着密切的关系。其中物理实际系统与仿真系统基本关系可表示成图1。

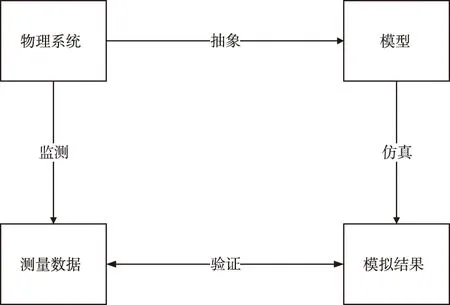
图1 实际系统与仿真系统关系简图

如上图所示通过对物理系统的抽象得到物理系统的映射模型(此文中为数学模型)；再建立计算程序算法仿真，得到仿真的模拟结果；最后，比较仿真模型模拟结果与实际物理系统的过程和状态参数(仿真对象)数据，此步骤是验证仿真的可用性和精度。

上述的仿真关系是基于模型的活动，其一般步骤如图2所示：

图2 仿真的一般步骤

第一步，要针对实际系统建立其形式化。此步骤一方面根据研究和分析的目的，确定模型的边界，因为任何一个模型都只能反映实际系统的某一部份或某一方面，也就是说，一个模型只是实际系统的有限映射。另一方面，为了使模型具有可行性，必须具备对系统的先验知识及必要的试验数据(本文中是包括了设备，工质等特性参数以及操作参数)。特别是，必须对模型进行形式化处理，以得到计算机仿真所要求的数学描述；

第二步，根据系统的特点和仿真的要求选择合适的算法，当采用该算法建立仿真模型时，其计算的稳定性、计算精度、计算速度应满足仿真的需要(此文中的仿真系统采用的是与实际系统1：1的仿真速度)；

第三步，将仿真模型用计算能执行的程序(本文所述的程序采用FORTRAN语言进行编程)来描述；

第四步，进行程序调试，检验所选仿真算法的合理性；

第五步，根据仿真的目的对模型进行多方面的试验，相应的得到模型的输出；

第六步，要对仿真输出进行分析。

在实际仿真时，上述每一步都需要多次反复和迭代。

1.2 数学模型简介

此文中的数学模型是基于实际系统状态和平衡态建立的动态模型，主要是基于能量守恒，质量守恒，动量守恒等三大守恒定理建立的非线性的连续性的动力系统模型。

本文介绍的流体力学中的伯努利定理，就是由机械能守恒推导而来的，在流体为不可压缩的条件下(γ为常数)，可以积分式(1)得单位重量能量：

(1)

这个著名得方程，称为伯努利定理，用以纪念这位瑞士物理学家丹尼尔·伯努利(1700-1782)，是他在1738年首先提出这条定理的。如将上式通乘以g，再通乘以ρ，即得到伯努利定理的另外的形式，即单位质量的能量：

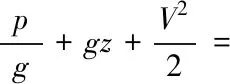
(2)

在实际应用上述方程时，需要基本假设，具体如下：

1)假设粘性(摩擦)效应可以略去不计。

2)假设流动是恒定的。

3)此流体是沿流线的。

4)假设流体是不可压缩的。

5)假设沿流线没有能量加进或移出流体。

此文中的仿真对象是水电站的引水系统，此系统是连接水轮机和上游水库的通道，由电站进水口、压力管道、地下厂房、尾水调压室、尾水隧洞和尾水出口等建筑物组成。

此次建立的仿真系统的对象主要仿真参数为进水口工作闸门流量特性仿真，压力管道压力和流量的关系仿真，蜗壳进口压力等仿真。

对上述仿真对象进行系统抽象后得到，包括上游水库，闸门，引水钢管，水轮机，尾水库等仿真建模对象模块(此文所述的仿真系统就是以这些模块为基础，结合实际系统的情况融合而成)，其简单图示如图3。

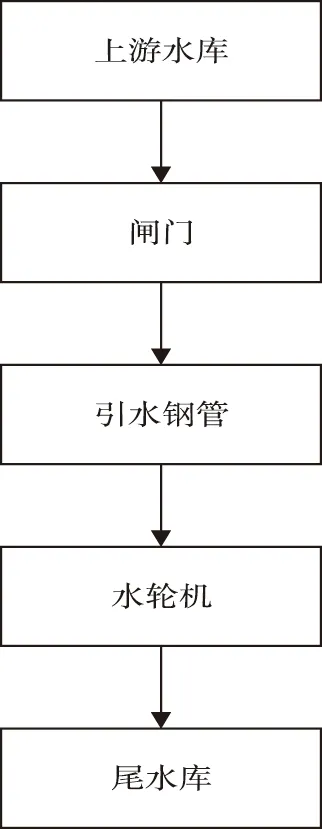
图3 引水系统仿真模块简图

2 基本原理模型

2.1 流体流量、压力模型

2.1.1 基本方程

流体流量和压力之间的关系可以在伯努利方程看出，假设工质为定常不可压缩流体，忽略黏滞性效应，流体元素沿着流线而流动。伯努利方程也可以用(3)式表示

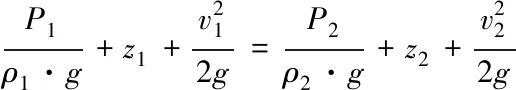
(3)

但在实际工程应用中，流体粘性总是不可忽略的，因此，粘性流体的伯努利方程可表示为

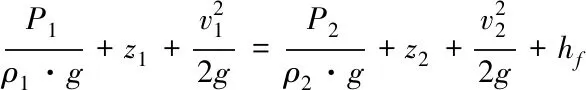
(4)

式(4)中，P1，P2为上、下游压力，单位为Pa，z1，z2为上、下游高度单位为米，m;ρ1，ρ2为上、下游流体密度，单位为kg/m3;υ1，υ2为上、下游流体流动速度，单位为m/s;g为重力加速度，单位为m/s2;hf为总压降，单位为米水柱。

粘性流体的压降，包括摩阻压降和形阻压降，其值皆与速度压头成正比

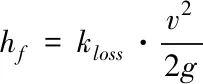
(5)

式(5)中，kloss为阻力系数；v为流体流速，m/s。

式(4)中，速度压头v2/2g，通常并不显著，在大多数实际情况下可忽略，不可压缩流体且密度为常数：ρ=ρ1=ρ2。(2)式可变为：

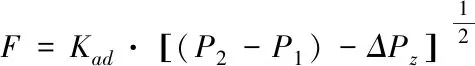
(6)

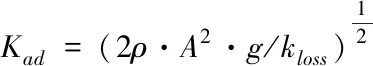
(7)

ΔPz=ρ·(z1-z2)

(8)

式中，A为流通面积，m2;F为流量，kg/s。

式(6)即为仿真模型中用到的流量—压力关系式。

2.1.2 仿真处理

将(6)式进行线性化处理。(6)式可改写为：

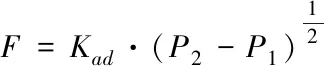
(9)

并可线性化为

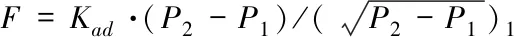
(10)

此文中的仿真模型采用FORTRAN语言进行编程，它是为科学、工程问题或企事业管理中的那些能够用数学公式表达的问题而设计的，其数值仿真计算的功能较强。源程序不再此文中累序。

下面通过第3节简述仿真的界面和模拟结果，以及与实际系统的参数数据。

3 举例

以本厂水电站引水系统为例，包括进水口拦污栅、机组进水口闸门、压力管道、调压室、尾水闸门等，系统仿真界面如图4：

图4 引水系统界面

从图3中看出，引水系统的水流程。从P2为闸后水位(1124m)，P1为尾水水位(955.9m)，因此，通过(10)式可以计算出进入水轮机的流量(其中尾水水位为常值)。保持水位差基本不变的情况下，关闭进水闸门，其仿真与实际流量的数据如下表：

表1中的开度操作是通过建立闸门控制仿真模型进行操作的(控制模型是根据实际系统的控制逻辑进行仿真建模，实现对实际系统的1：1的仿真模型)，操作仿真界面如图5。

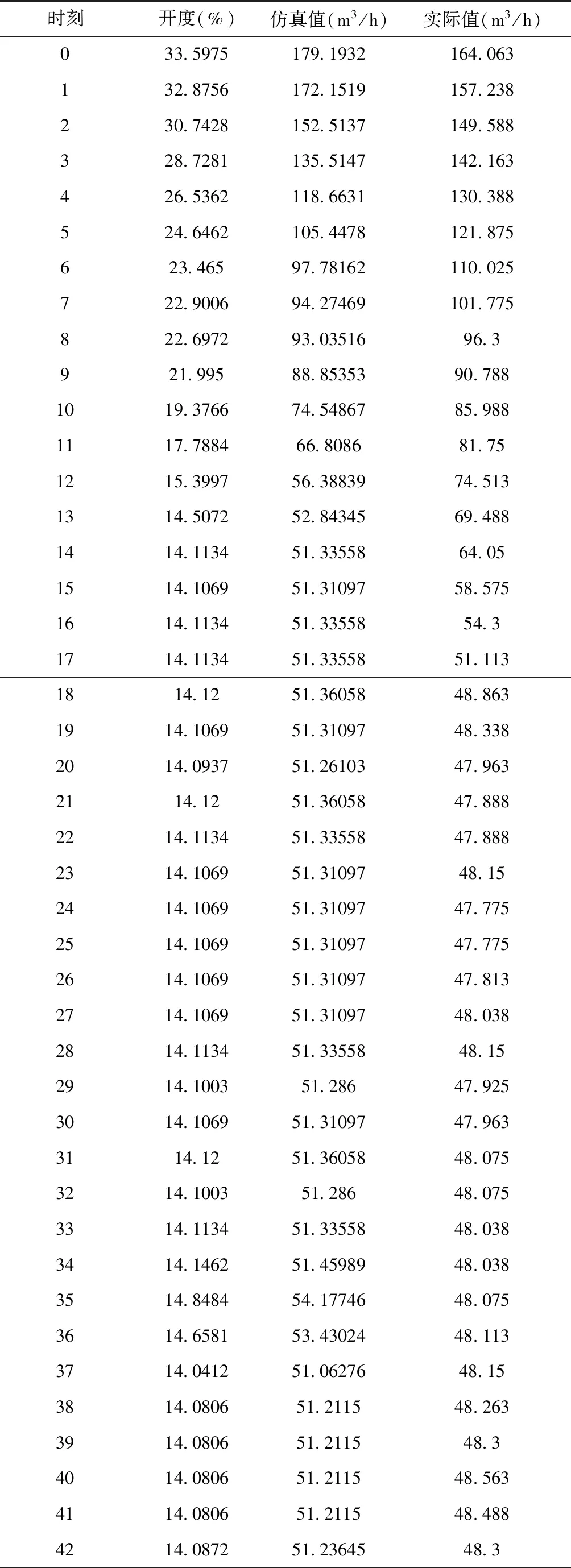
表1 开度-流量数据表

时刻开度(%)仿真值(m3/h)实际值(m3/h)4314.100351.28648.154414.034751.0382547.8134510.609139.2720647.55464.683122.4531444.55470.61447.81921638.7480.60787.77698832.85490.60787.77698823.4500.60787.77698817.363510.61447.81921610.875520.62757.9023746.788530.61447.8192164.088540.61447.8192163.975550.60787.7769884.05560.61447.8192164.163570.32565.6893214.163580.31915.6322023.075590.31915.6322022.363600.31915.6322021.05

图5 闸门操作控制仿真界面

通过操作闸门控制界面的关闸按钮，仿真系统会进行实时的仿真，得到如表1的数据，而开度与流量静态关系图(横坐标为归一化后的开度，纵坐标为归一化后的流量数值)，如图6。

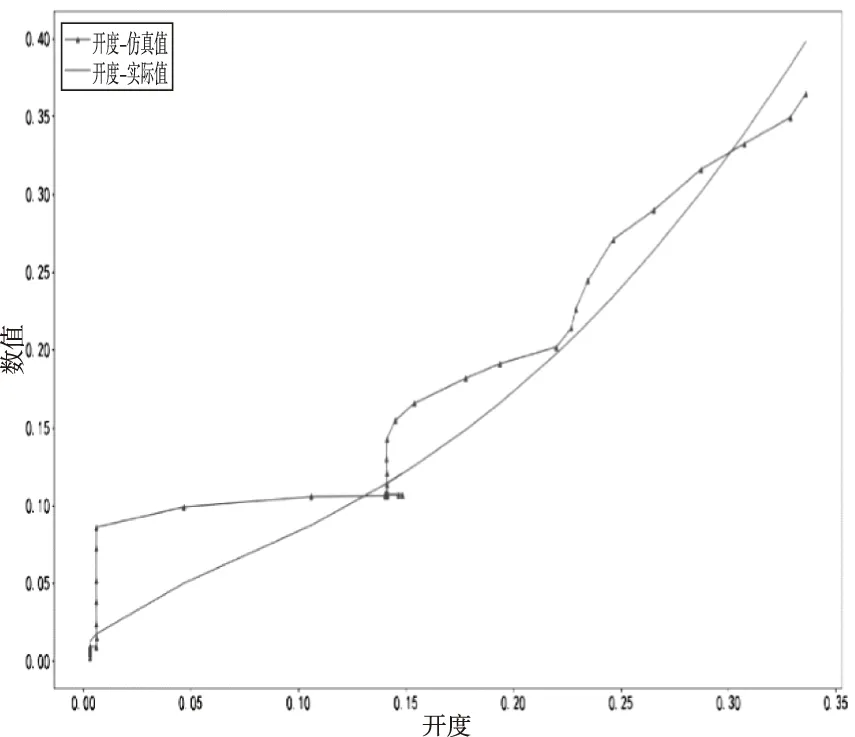
图6 开度与流量静态关系曲线

从图6可以看出，不管是实际流量，还是仿真流量都与闸门开度有比较明显的线性关系，说明仿真的流量静态特性是符合实际的。

仿真值与实际值的趋势曲线(横坐标为仿真时间，纵坐标为归一化后的数值)如图7。

图7 流量仿真-实际动态趋势曲线

从图7看出，在闸门开度关闭的过程中，仿真值与实际值的动态趋势是一致的，这说明流量仿真的动态特性是比较符合实际过程的。

以上介绍了闸门关闭过程的仿真结果数据和实际数据，并通过图示的方式呈现两者的数据趋势。闸门开启过程的仿真结果数据和实际数据是关闭过程的逆过程数据，在此文中就不再累叙。

下面简单介绍水轮机蜗壳压力与闸门开度的仿真结果，通过(8)计算得到下表仿真结果(数据为归一化)。

表2 开度-压力-水位仿真结果

当关闭进水闸门时，其仿真的趋势曲线(横坐标为仿真时间，纵坐标为归一化后的数值)如图8。

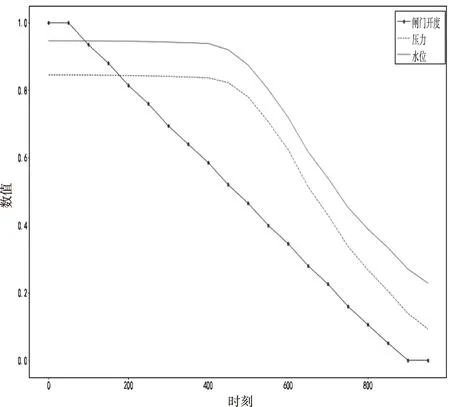
图8 水轮机蜗壳进口压力仿真曲线

从图8中看出，蜗壳进口压力主要是受闸后水位影响，这表明蜗壳压力主要表现在静压上，既测点所处的水深压力。

4 结论

此文介绍了利用伯努利原理建立流量-压力的数学模型，对数学模型采用FORTRAN编程，并通过仿真平台模拟引水系统的流量压力的静态和动态特性。

在与实际测量值比较时可以看出，不管静态特征，还是动态趋势，都能够满足系统仿真的精度要求，满足水电站培训的需要，为水电站操作员提供了很好的技能实训平台。