基于非等间隔GM模型的船舶柴油机性能参数预测研究

肖润 祖象欢 李业鹏 杨传雷

摘要： 针对采样间隔不等时传统GM模型失效问题，以TBD234V12相继增压柴油机为研究对象，分别采用加权处理和等时距变换对原模型进行改进，对两种模型应用于柴油机不同运行参数的预测效果进行了对比研究。试验及仿真验证结果表明：加权处理和等时距变换均能有效改善原模型精度，但是前者效果明显优于后者，不同参数GM模型的预测相对误差最高为4.4%，最低为0.24%。

Abstract： Aiming at the invalidation of traditional GM model when sampling interval is unequal， the TBD234V12 sequential turbocharged diesel engine is taken as the research object. The original model is improved by equal time-distance transformation and weighting method respectively. The prediction effects of the two models applied to different operating parameters of diesel engines are compared. The experimental and simulation results show that both the two methods can effectively improve the accuracy of the original model， but the effect of the former is obviously better than that of the latter， the maximum relative error of GM model with different parameters was 4.4% and the minimum was 0.24%.

关键词： 柴油机;性能参数;GM预测;非等间隔

Key words： diesel engine;performance parameters;GM prediction;non-equal interval

中图分类号：TK427                                      文献标识码：A                                  文章编号：1674-957X（2021）23-0014-04

0  引言

增压柴油机长期工作在高温、高压及高转速的环境下，如何有效保证柴油机的安全运行至关重要[1-2]。目前普遍采用的方法是基于多传感器信息融合技术，实时在线监测柴油机主要运行参数的状态趋势[3]。但是，在实际数据采集过程中，往往出现一定滞后性，而且某些故障一旦发生，将对柴油机带来不可恢复的损害。因此，在现有的参数监测的基础上，融入在线预测功能，实现未来时刻的关键参数运行状态和趋势的预测，从而达到故障信息监测的目的，防患于未然。

目前，有关性能参数预测的方法比较多，以人工智能预测算法应用最为广泛。比如神经网络[4-5]、支持向量机[6-7]及贝叶斯网络[8-9]等。此类方法均属于大数据发掘技术，通过大量数据反复训练来获取理想精度的预测模型，具有很强的非线性映射能力[10]。但是，此类方法的缺点也比较明显，那就是对数据样本的要求较高、硬件要求高等，特别是针对小样本预测问题，此类方法便难以奏效。而灰色预测方法的诞生则为小样本预测问题开辟了一种新的研究道路。

灰色预测方法是由1982年中国学者邓聚龙教授提出的灰色系统理论中的重要理论分支，代表模型即GM预测模型，旨在解决小样本、贫数据预测问题。自该方法创立以来，已经成功应用于金融、管理、运输等多个领域[11]。由于理论仍处于不断完善阶段，GM预测在柴油机领域的应用还比较薄弱[12]。因此，本文以TBD234V12相继增压柴油机为研究对象，对采样间隔不等时传统模型建模失效问题进行了优化应用研究，为GM预测在柴油机领域的拓展应用以及模型的优化提供一定理论参考。

1  传统GM模型

GM（1，1）模型是灰色预测理论中的基本模型，也是应用最为广泛的模型，简称GM模型，通常所提的GM模型均代指该模型，具体的建模过程如下：

已知原始序列：

则GM（1，1）的原始形式为：

其中，x（0）（k）称为x（1）（k）的灰导数，a称作发展系数，b称作灰作用量。

已知GM（1，1）模型均值形式的白化微分方程：

其通解为：

同理，结合初始条件及待辨识参数α=[a，b]T可求得最终的时间响应式：

在传统GM模型中，原始序列均是由相同采用时间间隔的数据点构成，即原始序列必须滿足时序性。

2  非等间隔GM改进模型

当数据采样间隔不等时，原始序列不满足时序性这一建模基本条件，因此需要对原模型进行改进。本文采用等时距变换和加权处理两种改进方法，重点讨论两种不同方法应用于柴油机主要运行参数GM预测建模中的区别。

2.1 基于等时距变换的改进模型

假设非等间隔原始序列为：

各采样时刻平均间隔：

则各实际采样时刻与平均时段单位时差异系数可以定义为：

各实际时段总的差值：

则可以得到等间隔点的灰数值：

对进行等间隔GM建模。本节选取EGM建模并求得最终的预测模型：

2.2 基于加权处理的改进模型

假设非等间隔原始序列为：

定义相邻两次采样时刻之间的时间间隔为累加权值系数，生成新的累加序列，并得到新的紧邻均值生成序列：

其中，当k=1时Δtk=1。同理，对X（1）进行EGM建模，求解白化微分方程的相应函数：

根据公式还原可得到模型解：

3  结果验证

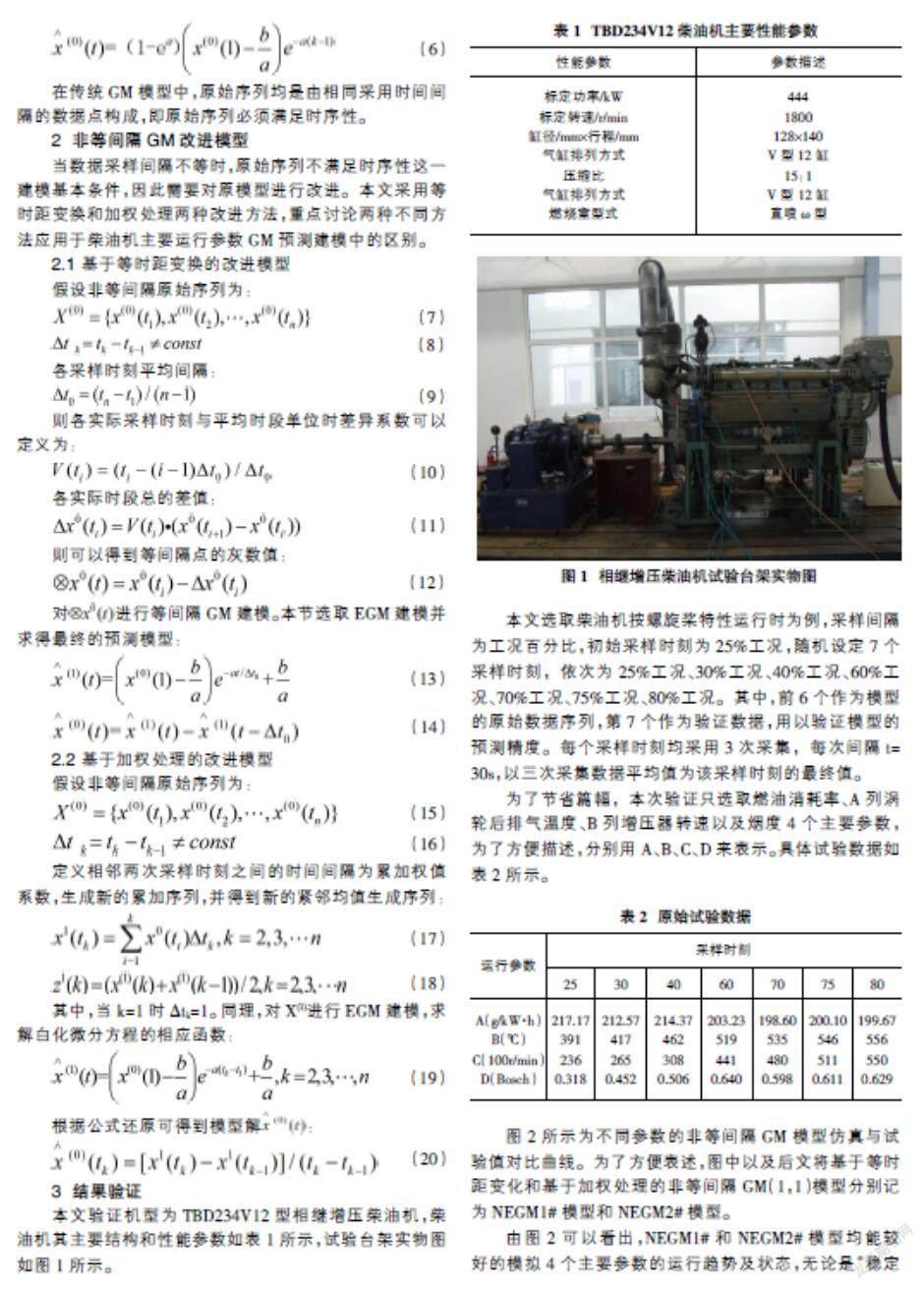
本文验证机型为TBD234V12型相继增压柴油机，柴油机其主要结构和性能参数如表1所示，试验台架实物图如图1所示。

本文选取柴油机按螺旋桨特性运行时为例，采样间隔为工况百分比，初始采样时刻为25%工况，随机设定7个采样时刻，依次为25%工况、30%工况、40%工况、60%工况、70%工况、75%工况、80%工况。其中，前6个作为模型的原始数据序列，第7个作为验证数据，用以验证模型的预测精度。每个采样时刻均采用3次采集，每次间隔t=30s，以三次采集数据平均值为该采样时刻的最终值。

为了节省篇幅，本次验证只选取燃油消耗率、A列涡轮后排气温度、B列增压器转速以及烟度4个主要参数，为了方便描述，分别用A、B、C、D来表示。具体试验数据如表2所示。

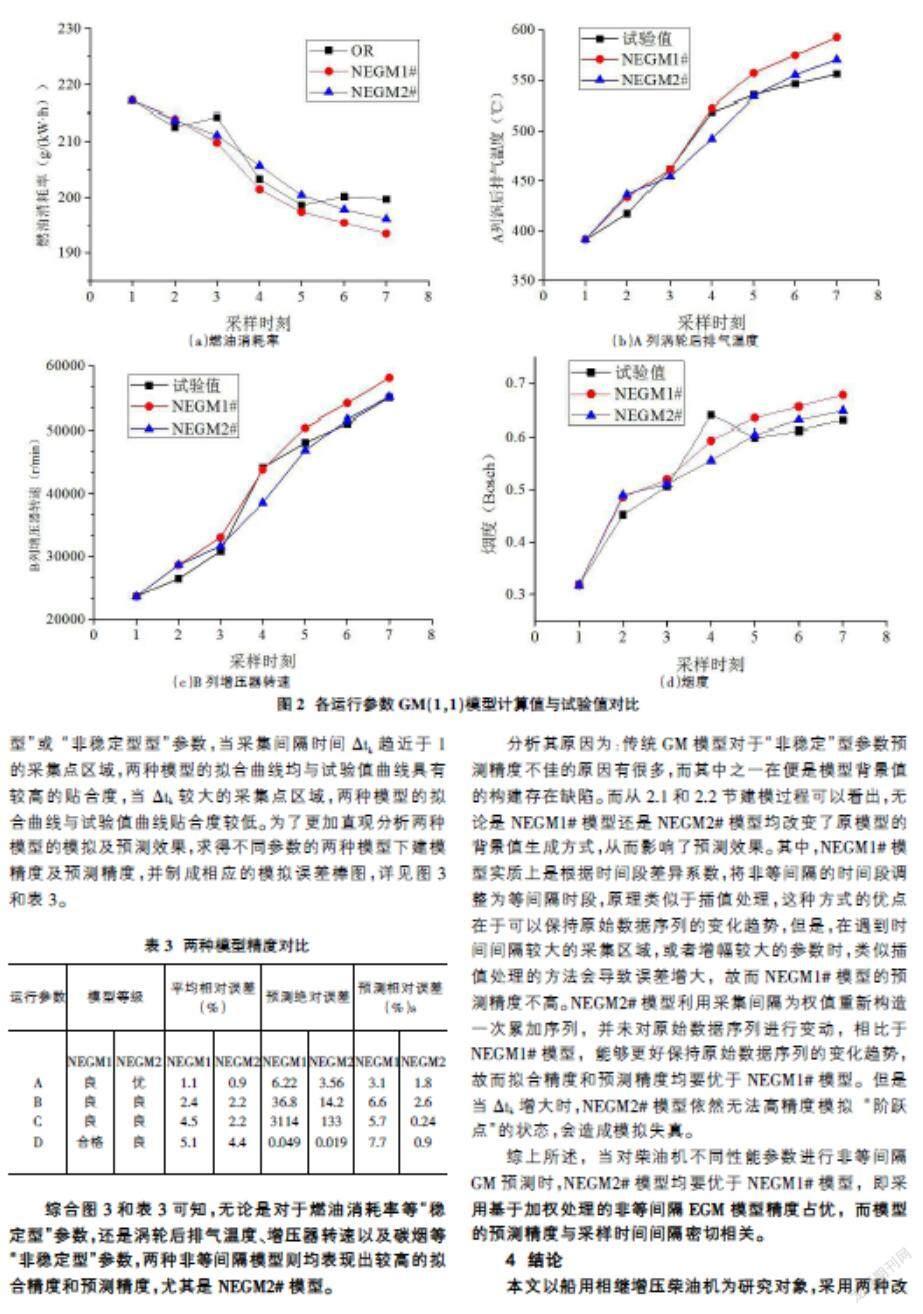
图2所示为不同参数的非等间隔GM模型仿真与试验值对比曲线。为了方便表述，图中以及后文将基于等时距变化和基于加权处理的非等间隔GM（1，1）模型分别记为NEGM1#模型和NEGM2#模型。

由图2可以看出，NEGM1#和NEGM2#模型均能较好的模拟4个主要参数的运行趋势及状态，无论是“稳定型”或 “非稳定型型”参数，当采集间隔时间Δtk趋近于1的采集点区域，两种模型的拟合曲线均与试验值曲线具有较高的贴合度，当Δtk较大的采集点区域，两种模型的拟合曲线与试验值曲线贴合度较低。为了更加直观分析两种模型的模拟及预测效果，求得不同参数的两种模型下建模精度及预测精度，并制成相应的模拟误差棒图，详见图3和表3。

综合图3和表3可知，无论是对于燃油消耗率等“稳定型”参数，还是涡轮后排氣温度、增压器转速以及碳烟等“非稳定型”参数，两种非等间隔模型则均表现出较高的拟合精度和预测精度，尤其是NEGM2#模型。

分析其原因为：传统GM模型对于“非稳定”型参数预测精度不佳的原因有很多，而其中之一在便是模型背景值的构建存在缺陷。而从2.1和2.2节建模过程可以看出，无论是NEGM1#模型还是NEGM2#模型均改变了原模型的背景值生成方式，从而影响了预测效果。其中，NEGM1#模型实质上是根据时间段差异系数，将非等间隔的时间段调整为等间隔时段，原理类似于插值处理，这种方式的优点在于可以保持原始数据序列的变化趋势，但是，在遇到时间间隔较大的采集区域，或者增幅较大的参数时，类似插值处理的方法会导致误差增大，故而NEGM1#模型的预测精度不高。NEGM2#模型利用采集间隔为权值重新构造一次累加序列，并未对原始数据序列进行变动，相比于NEGM1#模型，能够更好保持原始数据序列的变化趋势，故而拟合精度和预测精度均要优于NEGM1#模型。但是当Δtk增大时，NEGM2#模型依然无法高精度模拟“阶跃点”的状态，会造成模拟失真。

综上所述，当对柴油机不同性能参数进行非等间隔GM预测时，NEGM2#模型均要优于NEGM1#模型，即采用基于加权处理的非等间隔EGM模型精度占优，而模型的预测精度与采样时间间隔密切相关。

4  结论

本文以船用相继增压柴油机为研究对象，采用两种改进GM建模方法对柴油机性能参数进行了非等间隔GM预测，有效解决了小样本灰色预测过程中，采样间隔不等时传统GM模型失效的问题。通过对比研究发现，基于加权处理的改进模型的优化效果明显优于基于等时距变换的改进模型，而采样时间间隔对两种改进模型的精度具有决定性作用。由于试验条件限制，验证参数比较有限，但是并不影响本文技术思路的有效性，下一步工作将对更多参数进行补充验证，从而获得具有高度普适性的预测模型，为船舶柴油机的性能参数预测提供新的技术工具。

参考文献：

[1]杨传雷，王银燕，王贺春，崔欣洁，杜剑维.基于dSPACE的柴油机相继增压系统试验研究[J].内燃机工程，2012，33（03）：88-92.

[2]ZU Xianghuan， YANG Chuanlei， WANG Yinyan. Performance prediction of a sequential turbocharging diesel enginebased on GM （1，1） model and MATLAB GUI[J].Journal of Harbin Engineering University.2015，36（11）：1-5.

[3]刘罡.基于信息融合的柴油机故障诊断方法研究[D].大连海事大学，2015.

[4]Rezaei J， Shahbakhti M， Bahri B， et al. Performance prediction of HCCI engines with oxygenated fuels using artificial neural networks[J]. Applied Energy，2015，138：460-473.

[5]Roy S， Banerjee R， Bose P K. Performance and exhaust emissions prediction of a CRDI assisted single cylinder diesel engine coupled with EGR using artificial neural network[J]. Applied Energy，2014，119：330-340.

[6]Huang C L， Tsai C Y .A hybrid SOFM-SVR with a filter-based feature selection for stock market forecasting[J].Expert Systems with Applications，2009，36（2）：1529-1539.

[7]Liu B， Hu J， Yan F， et al. A novel optimal support vector machine ensemble model for NOX emissions prediction of a diesel engine[J]. Measurement， 2016， 92：183-192.

[8]Zaidan M A， Harrison R F， Mills A R， et al. Bayesian Hierarchical Models for aerospace gas turbine engine prognostics[J].Expert Systems with Applications，2015，42（1）：539-553.

[9]Ziani R， Ouali M S， Artiba A. Sensibility of Bayesian inference methods for reliability prediction of ageing systems， case of Diesel locomotives[J]. International Journal of Production Research，2014，52（14）：4142-4155.

[10]邹蕾，张先锋.人工智能及其发展应用[J].信息网络安全，2012（02）：11-13.

[11]刘思峰.灰色系统理论的产生与发展[J].南京航空航天大学学报，2004（02）：267-272.

[12]李华兵，黄进明，荣礼.灰色预测理论在船舶机械故障诊断中的应用[J].上海海事大学学报，2017，38（03）：85-89.