面向高精度城市测绘的激光紧耦合SLAM方法
2021-12-09孙喜亮关宏灿苏艳军徐光彩郭庆华
孙喜亮,关宏灿,苏艳军,徐光彩,郭庆华
1. 中国科学院植物研究所植被与环境变化国家重点实验室,北京 100093; 2. 中国科学院大学,北京 100049; 3. 北京大学城市与环境学院,北京 100871
近年来,集成了激光雷达(light detection and ranging,LiDAR)、惯性测量单元(inertial measurement unit,IMU)和全球导航卫星系统(Global Navigation Satellite System,GNSS)的移动激光雷达平台被广泛用于获取城市三维地理信息数据[1-2]。GNSS/IMU组合导航是目前移动测量平台最常用的定位方法,然而由于高楼、桥梁、隧道、行道树等城市地物对GNSS信号的遮挡,城市中易存在大量弱、无GNSS信号区域,仅凭这种定位方法难以有效实现大范围城市场景的高精度制图[3]。激光同时定位与地图构建(simultaneous localization and mapping,SLAM)技术可利用激光雷达增量式构建地图的同时,实现移动测量平台自身的相对定位,为解决弱、无GNSS信号环境下的制图问题提供了有效的解决方案[4],从而被广泛应用于高精度制图中[5-6]。
目前,激光SLAM方法按照激光和IMU的融合方式可分为松耦合和紧耦合[7-9]。松耦合方法独立计算激光和IMU各自的运动量,然后,对它们的位姿估计结果进行融合。文献[10]提出的LOAM方法是目前较为经典的松耦合方法,该方法通过结合高频里程计粗定位和低频建图精定位的方式,实现了基于旋转2D LiDAR的同步定位和制图。文献[11]在LOAM的基础上,引入视觉里程计作为激光里程计的前端,形成了V-LOAM方法,进一步提高了SLAM的精度。文献[12]在LOAM基础上,利用点云分割降低特征数量,结合两步配准和闭环约束削弱累积误差,形成了适合地面无人车的LeGO-LOAM方法。然而,松耦合方法未能联合优化各传感器的观测量,在特征缺乏区域易存在累积误差大、稳健性差等问题[4]。
与松耦合方法相比,紧耦合方法直接融合了激光原始特征信息和惯性单元测量值等输出运动状态量,具有稳健性强且制图精度高的优点[8]。近年来,多种紧耦合方法被相继提出。例如文献[13]将IMU预积分值应用到点云的运动畸变补偿中,实现了LiDAR和IMU的外参校正;文献[14]基于视觉惯性紧耦合SLAM方法引入了一种紧耦合的激光惯导SLAM框架,联合优化激光雷达特征点和IMU的观测量,与LOAM相比获得了更准确的结果,但是其效率较低,惯导初始化条件复杂,场景特征缺乏区域稳健性较差。文献[15]提出了一种以机器人为中心的激光雷达惯性状态估计器R-LINS,该方法利用迭代误差状态卡尔曼滤波器修正了机器人的状态估计,但存在长期运行会产生漂移的问题。文献[16]提出一种面向移动机器人的激光惯导紧耦合实时定位方法,该方法具有较好的实时性,但在开阔的室外环境下定位精度达分米级。文献[17]构建了基于因子图的紧耦合激光惯导里程计框架(LIO-SAM),将不同来源的IMU预积分因子、激光里程计因子、GNSS因子和闭环环因子进行联合优化,取得了较高的测图精度,但该方法只是简单地将GNSS因子加入联合优化中,未考虑复杂环境下GNSS异常对SLAM结果的影响。总体而言,目前已有方法主要针对小范围的室外街道或室内建筑场景,应用的地理覆盖范围有限,在场景复杂、GNSS信号不稳定、制图范围广且精度要求高的城市测绘应用中仍存在着累积误差大、稳健性差的问题[18-19]。
为了解决城市移动测量制图的难点,本文在LOAM和LeGO-LOAM的基础上,融合了差分GNSS轨迹、惯性测量单元位姿、激光序列帧数据开展高精度SLAM制图。本文的主要贡献可归纳为:①针对城市地物形状特性,联合杆状和面状特征点,采用先高程方向后水平方向的两步优化策略实现激光序列帧的相对位姿估计,提高了局部地图配准精度,降低了城市环境下SLAM的累积误差。②针对GNSS信号不稳定的特点,在全局地图构建及优化过程中增量式的加入GNSS角点构成的位置因子约束,实现了复杂城市场景下厘米级的高精度制图。
1 总体框架设计
本文提出的紧耦合激光SLAM算法在LOAM和LeGO-LOAM的基础上,融合了IMU预积分因子和GNSS因子,并在激光序列帧数据的初始相对位姿估计和全局地图构建及优化中分别引入了杆状和面状特征点和多因子联合优化的策略。如图1所示,本文提出的紧耦合激光SLAM系统可分为7个模块。
(1) IMU预积分。根据IMU运动方程对采样间隔的观测量进行积分,获取激光点云序列帧时刻对应位姿。
(2) 激光运动补偿和特征提取。利用IMU积分得到的相对运动位姿修正点云的运动畸变,随后提取杆状和面状特征点。
(3) 特征匹配和相对位姿估计。匹配序列帧同名特征,利用Levenberg-Marquardt(L-M)方法求解获取相邻帧的相对运动位姿。
(4) 局部地图构建及优化。联合序列帧同名特征点、初始相对位姿、IMU预积分因子优化构建局部地图。
(5) 闭环检测。新的局部地图构建完成后与历史局部地图进行特征匹配检测闭环。
(6) GNSS位置因子构建。依据GNSS轨迹方位变化提取出GNSS角点构成GNSS位置因子。
(7) 全局地图构建及优化。当前局部地图与历史地图存在闭环,则联合局部地图相对位姿、GNSS位置因子、IMU预积分因子、闭环因子等优化构建全局地图,不存在闭环则直接更新全局地图。
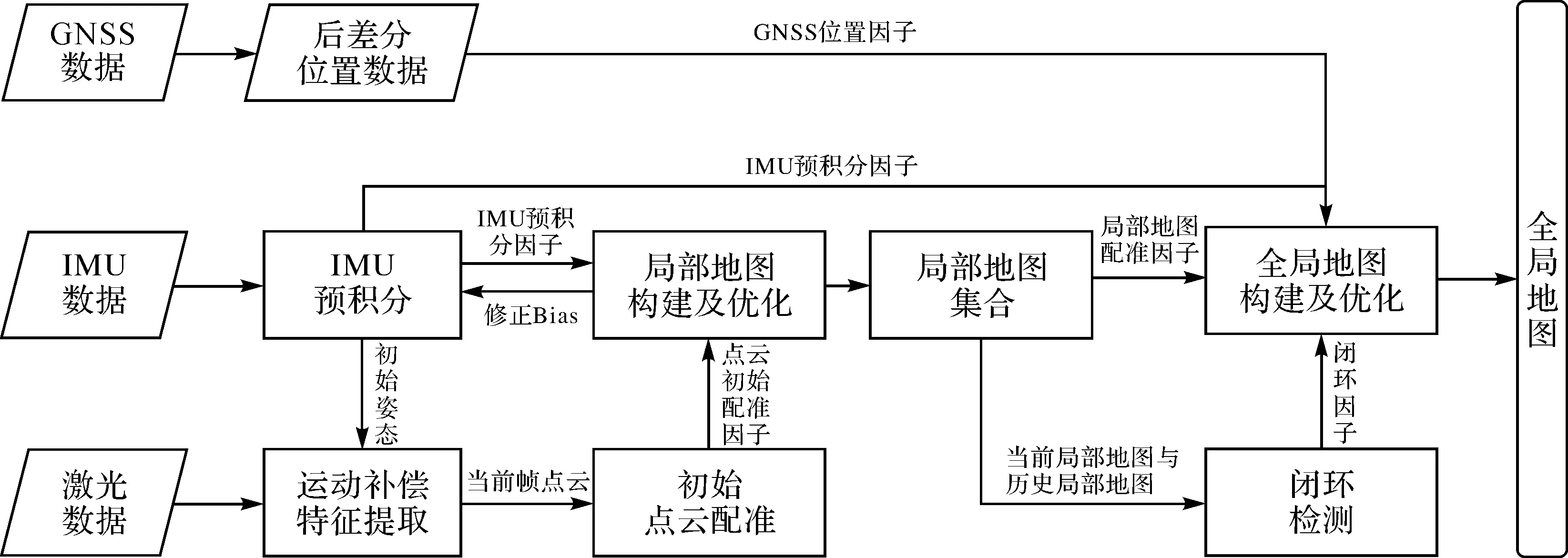
图1 系统框架Fig.1 Framework of the proposed method
2 基于特征点匹配的相对位姿估计
准确估计激光序列帧的相对位姿是构建局部地图的必要前提。本文采用IMU预积分的方式获得激光序列帧对应时刻的相对运动[13-14],基于此消除移动平台位姿变换所引起的运动畸变。在实现各单帧点云的畸变纠正后,通过配准得到激光序列帧数据的初始相对位姿估计。在点云配准中,迭代最近点(iterative closest point,ICP)算法是目前最常用的配准方法,然而由于城市场景移动测量数据采集中易存在大量的移动目标,且往返区域遮挡现象严重,直接基于原始激光点数据的ICP配准失败率高,因此本文采用基于特征点的配准方法,通过特征匹配得到同名特征点后,利用L-M法迭代求解激光序列帧间的相对位姿。
2.1 特征点提取
考虑到相对位姿估计中地面点对于垂直方向的约束较好,而杆状点和面状点则对水平方向的平移和旋转的约束较好,本文先进行地面点和非地面点的区分,随后进一步在非地面点中提取杆状和面状特征点[20-21],具体处理流程如下:
(1) 首先将单帧扫描获取激光点集ρt={ρ1,ρ2,…,ρn}生成深度图像(c,r),其中每个点ρi对应深度图像的一个像素,c和r分别为图像的列数和行数,图像深度值为ρi到传感器中心的距离。

(3) 获取角度图像后进一步利用Savitsky-Golay滤波算法进行平滑处理以削弱噪声的影响。最后将最低行中角度小于45°的所有像素标记为初始地面,并利用广度优先算法(breadth-first search,BFS)在角度图像上搜索与地面像素间角度差值小于5°的像素,将其标记为地面像素[22]。
(4) 根据地面像素,将其对应的点云标记为地面特征点fg,其余为非地面点,并对各地面点计算其法向nfg。
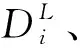
(1)
(2)
2.2 特征匹配和相对位姿估计
本文通过不同帧间特征点的匹配得到同名特征点[25],对于每一个特征点,本文在其相邻帧的特征点集中利用KDtree搜索其最邻近的同属性特征点,并将法向和主方向夹角均小于5°,且距离小于1 m的特征点对视为同名特征点[26-27]。同名特征提取后,联合点到线距离和点到面距离最小构建残差方程,利用L-M方法求解获取相邻帧的相对运动位姿[28]。考虑地面点对于垂直方向的约束较好,而杆状点和面状点则对水平方向的平移和旋转的约束较好,与直接求解6自由度位姿不同,本文采用了两步优化求解的策略,先利用地面点估算Z方向、横滚角、俯仰角的变化量,再利用杆状点和面状点估算X方向、Y方向、方位角的变化量,最终联合两步优化获取序列帧的相对位姿[12]。由于单帧点云稀疏且场景多样,无法保证配准的稳健性,且序列帧配准及IMU测量信息存在累积误差,因此本文选取1 s的点云数据建立局部地图,在获取激光序列帧相对位姿的基础上,融合IMU预积分测量信息,完成局部地图的构建,并将其与历史局部地图集合进行闭环检测,实现累积误差的削弱。
3 多因子联合的全局地图构建及优化
3.1 GNSS角点提取
全局地图构建及优化是生成高精度的全局一致性地图的关键步骤。GNSS位置因子可有效约束长距离轨迹(无闭环情况下)的漂移误差,但在城市复杂环境中,GNSS存在着位置精度不稳定的现象。此外,由于GNSS位置信息和激光惯导SLAM轨迹间没有初始的转换关系,其仅能约束XYZ位置而不能约束姿态,且在直线分布的轨迹中易存在歧义解。
为了提高GNSS位置因子的稳定性,本文在基于GNSS定位标准差剔除误差较大的GNSS点的基础上,进一步结合相同时间段内SLAM的轨迹距离和GNSS点位移动距离的差值约束剔除了GNSS中的虚假高精度点。此外,针对GNSS位置因子仅能约束XYZ,特别是在直线分布的轨迹中易存在歧义解的问题,本文提出了基于GNSS角点的位置因子约束方法,与直接使用GNSS位置因子不同的是,本文将GNSS位置段方位变化超过30°的GNSS点视为角点,在随后的全局优化中,增量式的加入GNSS角点,构成GNSS位置因子约束。
3.2 全局地图构建及优化
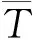
(3)
(4)
(5)
Eglobal=arcmin(rloop+rM+rimu+rgnss)
(6)
4 试验与分析
4.1 试验设备及数据介绍
为验证本文方法的有效性,采用了集成Velodyne VLP-16 LiDAR、Xsens MTI-100 IMU和Novatel 718D GNSS系统的背包式激光扫描平台对4种典型城市场景(开放园区、地下车库、城市公园、街区道路)进行了数据获取(图3)。
试验区中,开放公园整体为大型回环,场景中包含大量的建筑立面和少量移动车辆,轨迹总长度约为2.7 km,数据采集过程中存在少量往返采集。地下车库场景面积较小,轨迹总长度约为800 m,数据采集过程中场景内无移动目标干扰,但该场景GNSS信号较弱,存在GNSS信号丢失现象。城市公园场景内地物以树木为主,由于树木枝叶对激光扫描的遮挡,该场景内存在大量往返扫描。街区道路场景为笔直的城市主干道,扫描过程中存在大量移动车辆和行人的干扰,行走轨迹不存在闭环。各场景复杂情况和数据采集信息见表1。

表1 数据集概况
在上述4个场景中,研究将本文所提方法与目前主流的LOAM、LeGO-LOAM、LIO-SAM方法进行了对比,通过计算SLAM轨迹的绝对位置误差(absolute position error,APE)评定各方法的定位精度。同时,本文研究还对仅利用激光惯导进行SLAM制图(our-odom)和增加GNSS角点位置约束后的SLAM制图(our-method)结果进行了对比,以表明GNSS位置因子约束的有效性。
除定位精度的评定外,本文还在开放园区场景中,利用RTK(real-time kinematic)采集了20个控制点,用于评定点云制图的绝对坐标精度。
4.2 仅利用激光惯导的本文方法与不同SLAM方法的精度对比
不同场景下各SLAM方法的轨迹平面位置对比结果如图4所示。在开放园区场景中,局部放大图显示LeGO-LOAM方法的轨迹存在明显断裂(图4(a))。地下车库场景的局部放大图分别展示了车库入口和出口处轨迹结果,同样显示出LeGO-LOAM方法存在明显的轨迹跳变(图4(b))。城市公园场景中,由于LOAM和LeGO-LOAM方法精度较差,图中仅展示了LIO-SAM和本文方法的对比结果(图4(c))。街区道路场景中,结合表2的APE统计结果和图4(d)所示,可发现LIO-SAM方法APE误差主要出现在了Z方向上。
各场景下4种SLAM方法的轨迹APE随时间的变化情况如图5所示。在开放园区场景地下车库场景中,LeGO-LOAM方法出现点云配准失败情况后,误差直线上升(图5(a)和5(b))。城市公园场景中,LeGO-LOAM、LIO-SAM和本文方法的轨迹APE均随时间变化存在起伏(图5(c)),说明3种方法的闭环约束均削弱了累积误差的影响,且本文方法的累积误差最小。街区道路场景中,LIO-SAM存在较为严重的退化现象,APE随时间的增加显著上升。
精度评定结果表明(表2),LOAM方法在唯一成功的城市公园场景中,轨迹APE的RMSE高达32.406 m。LeGO-LOAM方法虽较LOAM方法有所提升,但其RMSE均在数十米量级。LIO-SAM方法在4个场景下均成功实现了制图,但最优精度出现在地下车库场景中,RMSEAPE为0.505 m。在开放园区、地下车库、城市公园、街区道路场景中,本文仅利用激光惯导的方法较LIO-SAM方法分别提升0.772 m、0.014 m、0.126 m和71.117 m。本文仅利用激光惯导的方法与LIO-SAM在街区道路和开放园区场景下的差异较大,其主要原因是两个场景中均存在较多的移动车辆,致使LIO-SAM方法点云配准发生退化现象,结果均表现为Z方向出现大的偏差。而本文方法提取了更趋近于静态目标的杆状和面状特征,并结合两步优化,有效地提高了点云配准的精度,削弱了累积误差。
4.3 GNSS角点位置约束的影响分析
如图5所示,加入GNSS角点位置约束有效降低了本文方法在4个场景下的累积误差。精度评价结果表明,4个场景的平均RMSEAPE由13.449 m提升至0.062 m(表3),其中在街区道路场景中的提升最为显著,主要原因在于该场景存在大量移动目标且移动轨迹不存在闭环,致使SLAM累积误差较大,此外,近似直线分布的GNSS点无法有效约束相应时刻的姿态,本文方法利用提出的GNSS角点约束有效提高了城市场景制图的稳健性和精度。

图2 全局地图构建及优化Fig.2 Global map construction and optimization
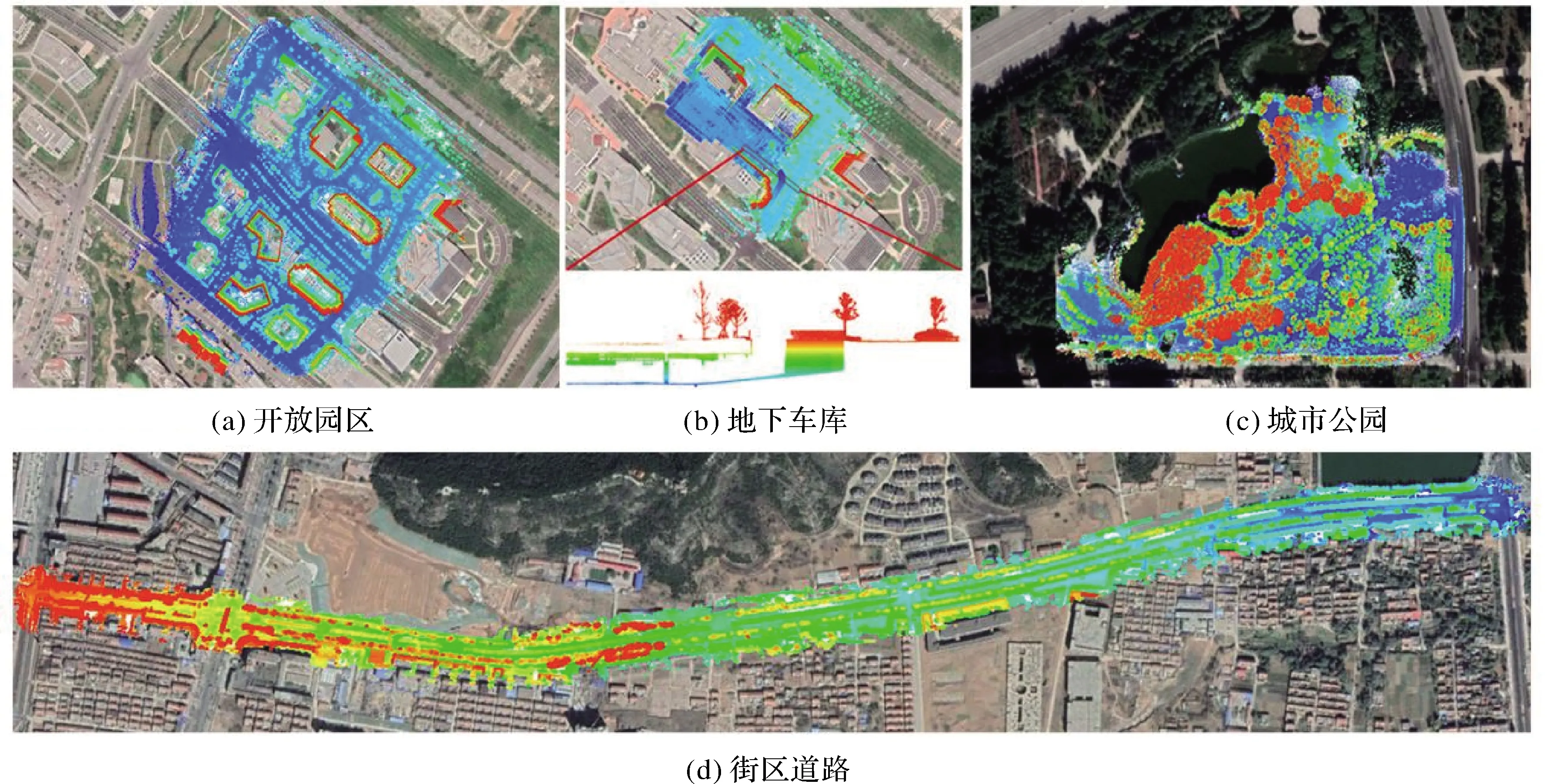
图3 试验区概况Fig.3 Overview of the study area
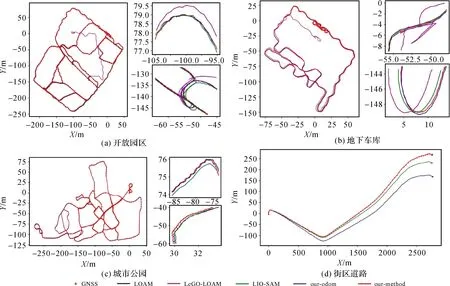
图4 SLAM轨迹平面位置对比Fig.4 Comparison between plane positions of SLAM trajectories

图5 SLAM轨迹APE对比Fig.5 Comparison between APE of SLAM trajectories
4.4 本文方法的点云制图精度分析
本文以开放园区为例,进一步展开本文方法点云制图结果的精度验证工作。试验采集了均匀分布于开放园区场景测区的20个有效的检查点(图6(a)),用于点云制图结果的绝对坐标精度验证。验证结果表明,本文所提方法制图结果的平面中误差为0.041 m,高程中误差为0.024 m,整体中误差为0.047 m(表4),检查点的平面和高程误差分布均为残留的随机误差(图6(b)),误差分布相对较大的点基本位于移动轨迹出现急剧方位变化之处,原因在于该处相对于平滑运动的轨迹而言仍有部分姿态误差残留,本文方法可有效提升SLAM制图的绝对坐标精度,满足复杂城市场景下的高精度制图要求。
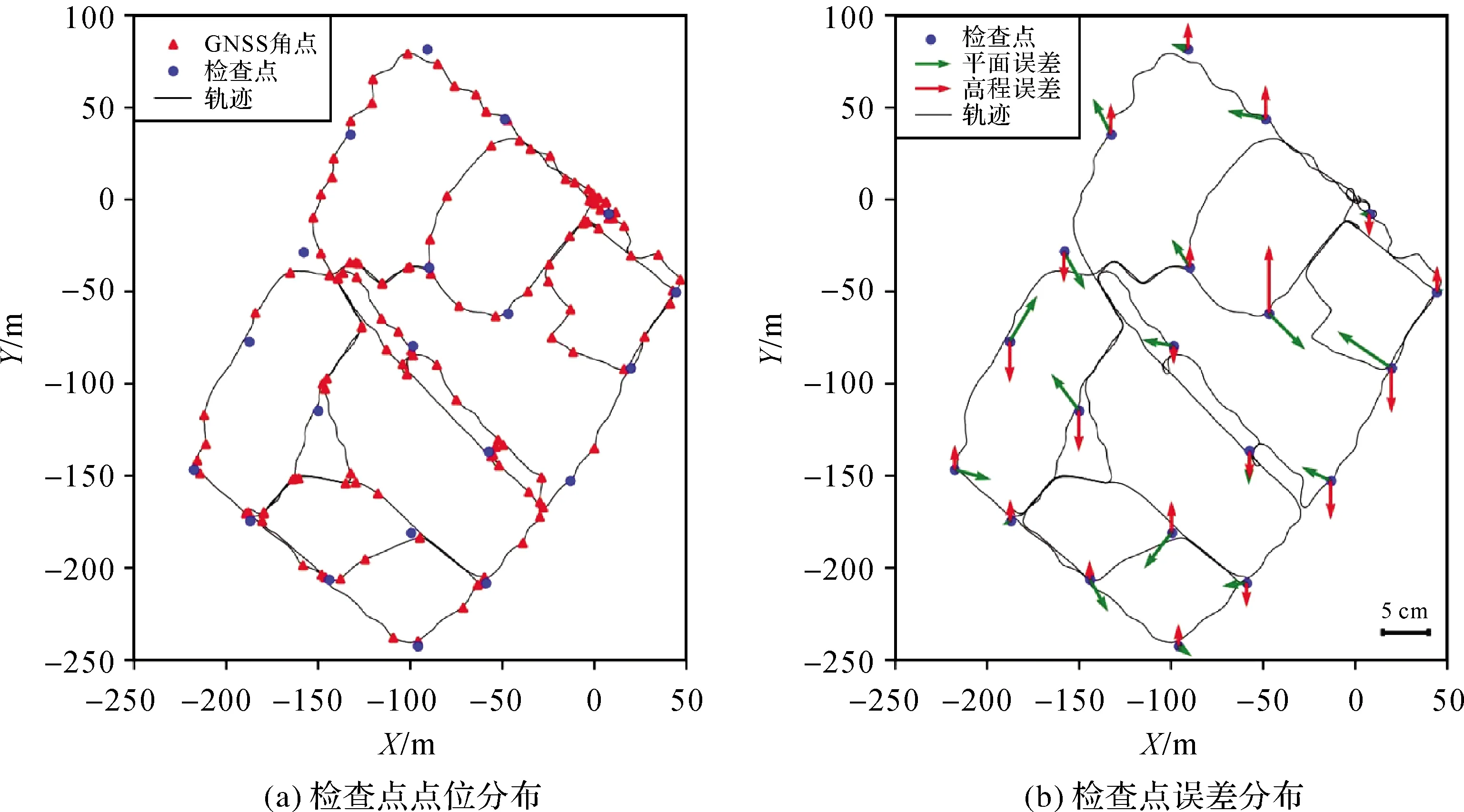
图6 检查点及误差分布Fig.6 Distribution of check points in the accuracy analysis
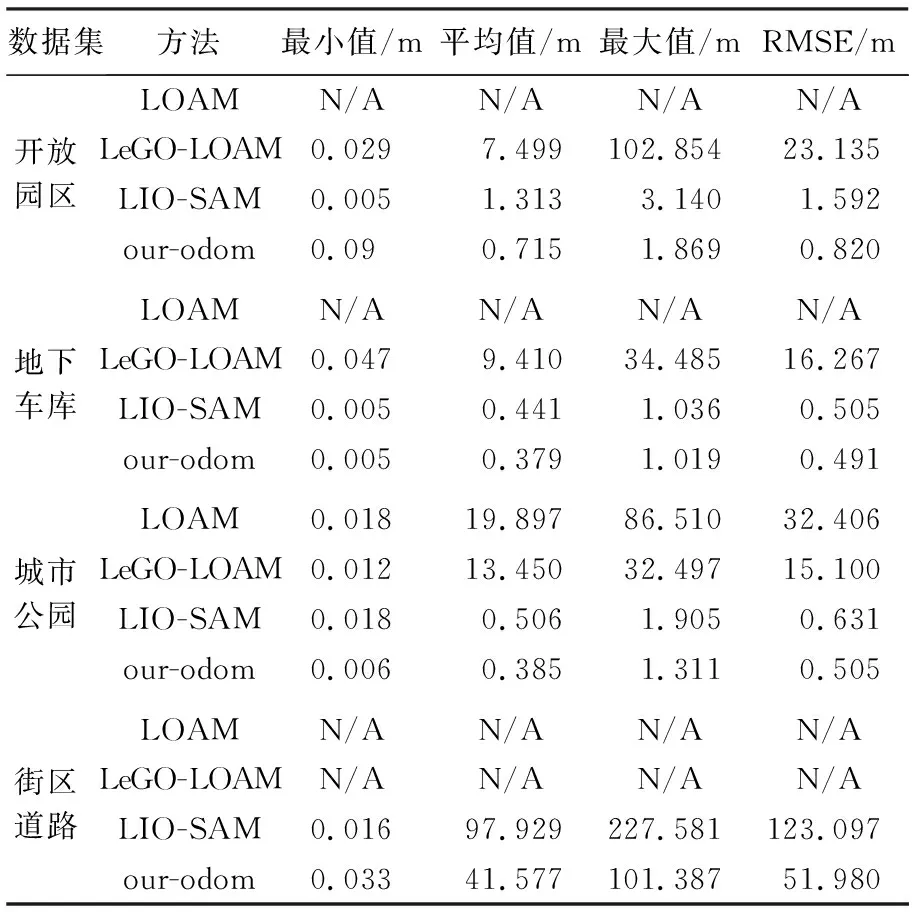
表2 SLAM轨迹APE统计结果
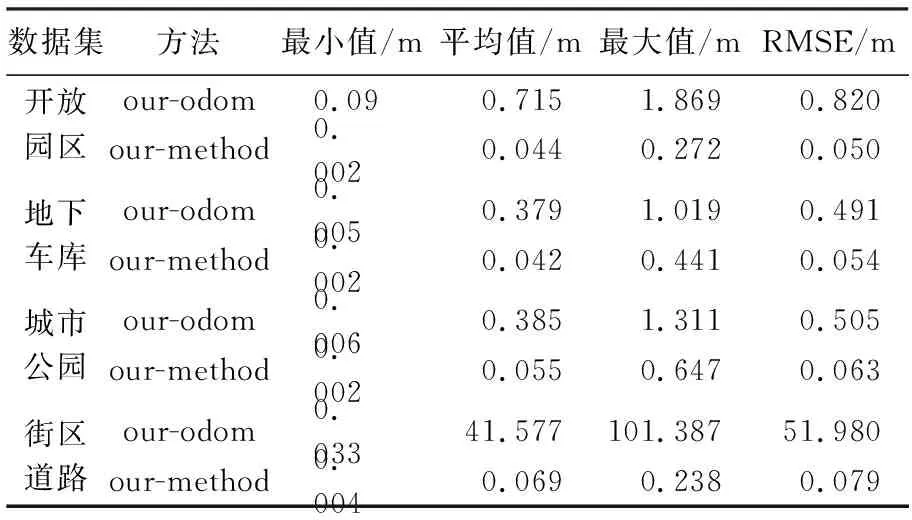
表3 有无GNSS角点位置因子约束的轨迹APE统计结果对比
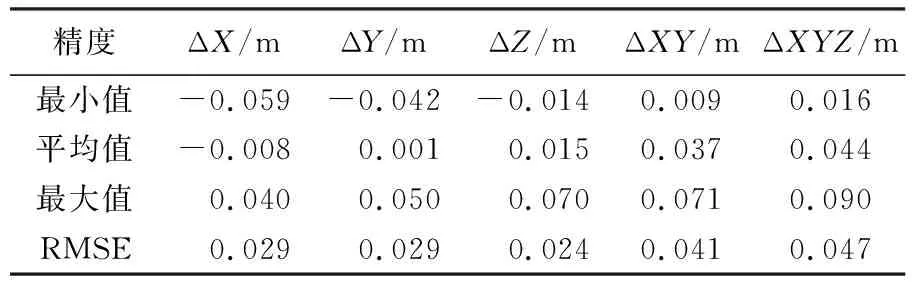
表4 检查点精度统计结果
5 结 论
本文面向复杂城市场景的高精度制图要求,提出了一种LiDAR、IMU、GNSS紧耦合SLAM方法,该方法利用杆状和面状特征进行序列帧间、激光扫描帧和局部地图间及局部地图间的点云配准,并采用GNSS角点位置约束SLAM,有效降低了城市环境下SLAM的累积误差,提高了全局地图构建的准确性。试验结果表明,LOAM和LeGO-LOAM方法稳健性及精度均较差,本文方法仅利用激光惯导进行SLAM制图时,在开放园区、地下车库、城市公园和街区道路场景中的精度(RMSEAPE=13.449 m)显著高于目前主流的紧耦合LIO-SAM(RMSEAPE=31.456 m)方法,结合GNSS位置因子约束后,精度提升至厘米级(RMSEAPE=0.062 m),其中开放园区中基于控制点的点云绝对坐标精度评价结果表明,本文方法(RMSE=0.047 m)可有效支持厘米级高精度城市制图。
