面向智能车的地下停车场环视特征地图构建与定位

周 哲，胡钊政，李 娜，肖汉彪，伍锦祥

1. 武汉理工大学智能交通系统研究中心，湖北 武汉 430063; 2. 武汉理工大学重庆研究院，重庆 401120; 3. 武汉理工大学自动化学院，湖北 武汉 430070

获取高精度室内定位信息是实现智能车全域自主行驶最关键的技术之一，也是实现车路协同的基础，受到工业界和学术界的广泛关注。目前，基于导航卫星的定位技术是室外环境中获取智能车位置信息的主流方法(如GPS、北斗)，但在室内环境中存在信号盲区等影响，难以满足智能车对定位精度的需求[1]。2020年，中国科协公布的十大工程技术难题，其中就包含“无人车如何实现在卫星不可用条件下的高精度智能导航”问题[2]。

为了实现在室内环境中的高精度定位，研究者提出多种定位方案，包括惯性导航系统(inertial navigation system, INS)[3]、无线传感网络[4]、激光雷达传感器[5]和视觉传感器[6]等。然而，随着运行时间的增加，INS产生严重的累积误差，不宜用于较大场景的定位。无线传感网络的定位原理与GPS较为相似，能够实现无累积误差定位，但存在不稳定性和使用成本等矛盾。激光传感器因使用成本高昂，使其难以大规模推广应用。相比之下，视觉传感器能够提供丰富的场景信息，而且价格低廉，因而，基于视觉的定位技术成为近几年的研究热点[7]。

近年来，研究者提出多种基于视觉的定位方法。其中，VSLAM(vision simultaneous localization and mapping)能够在未知的环境中实现精确的车辆定位[8]。然而，随着定位场景的增大，后端优化复杂度增加，且系统受累积误差的影响增大[9]。为了提高定位精度，降低计算负担，满足高级辅助驾驶的需求，高精度地图被认为是L3级及以上高级辅助驾驶的关键基础设施[10]。从而将定位过程分为视觉地图构建与基于地图的定位两个阶段[6,11]。定位阶段首先是要找到视觉地图中与当前图像最相似的地图节点，而后利用匹配的特征点计算当前车辆与地图之间的位姿关系完成定位。其中，基于稀疏特征(SIFT[12]、ORB[13])的匹配是最常用的地图匹配方法。文献[14]利用SIFT特征点匹配，获取最佳匹配，并利用PnP(perspective-n-point)解算在坐标系中的位置。文献[15]提出多视角的智能车定位方案，前视图像用来获取最佳的地图匹配节点，俯视图像计算当前车辆与地图之间的位姿关系，获取车辆在全局坐标系下的位置信息。文献[16]利用词袋模型(bag-of-word，BoW)通过层次化的匹配方案快速实现车辆的定位。文献[17]运用ICP算法计算路面标志与地图子图之间的位置关系，获取车辆在全局坐标系下的位置。文献[18]提出一种多视角、多尺度的智能车定位方法，将视觉地图的定位结果与视觉里程计的定位结果相融合，实现在地下停车场环境中0.45 m的平均定位误差。文献[19]利用环视图像获取地下停车场的语义信息并构建语义地图，采用图优化方法获得稳定的定位结果。文献[20]在seqSLAM序列匹配的基础上，采用“由粗到精”的匹配策略，并利用粒子滤波算法提出多分辨率的定位方法。但该序列匹配方法对车辆的行驶速度限制苛刻，且计算复杂度高，难以在移动平台上布设。

针对上述文献中的不足之处，本文在环视特征地图构建的基础上，提出基于二阶马尔可夫模型(Markov model，MM)的粒子滤波(particle filter，PF)算法(MM-PF)，实现稳定、准确的地图匹配，并利用局部特征点匹配计算当前车辆的全局位置，完成智能车在地下停车场的高精度定位，其新颖之处在于：①利用粒子(地图节点)之间的拓扑关系，构建基于二阶MM的粒子状态转移概率模型，将车辆运动约束与视觉信息相融合，提高地图匹配的准确性和稳定性。②为了提高算法的收敛效率，根据粒子的拓扑关系选取关键粒子，以降低计算复杂度。③提取场景的ORB全局特征，利用汉明距离构建当前图像与各粒子之间的观测概率模型，以降低计算负担。

1 本文方法

本文首先利用环视图像构建待定位场景的环视特征地图。在定位阶段，利用本文提出的二阶MM-PF算法获取与当前图像最相近的地图节点，完成节点级定位。而后在节点级定位的基础上，利用环视图像局部特征点匹配，求解当前车辆与环视特征地图之间的相对位姿，进而求解当前车辆在全局坐标系中的位置，完成度量级定位。具体包括环视特征地图构建和基于二阶MM-PF的智能车定位方法。

1.1 环视特征地图构建模型

特征地图是利用离散的节点对待定位场景进行表征，通过预先获取道路场景的视觉特征、结构等信息完成对场景的表征。本文利用文献[6,11]中的地图制作方法，并采用环视图像构建待定位场景的视觉地图，并称之为环视特征地图。通过获取环视图像特征、路面结构信息与位姿等组成地图节点，遍历待定位场景完成环视特征地图构建，地图结构如图1所示。在定位阶段，利用本文提出的二阶MM-PF算法实现车辆在地下停车场环境中的高精度定位。于是，可将环视特征地图定义为

P={p1,p2,…,pn}

(1)

式中，P表示环视特征地图数据库；pi表示环视特征地图的第i个节点；n为环视特征地图的节点数。

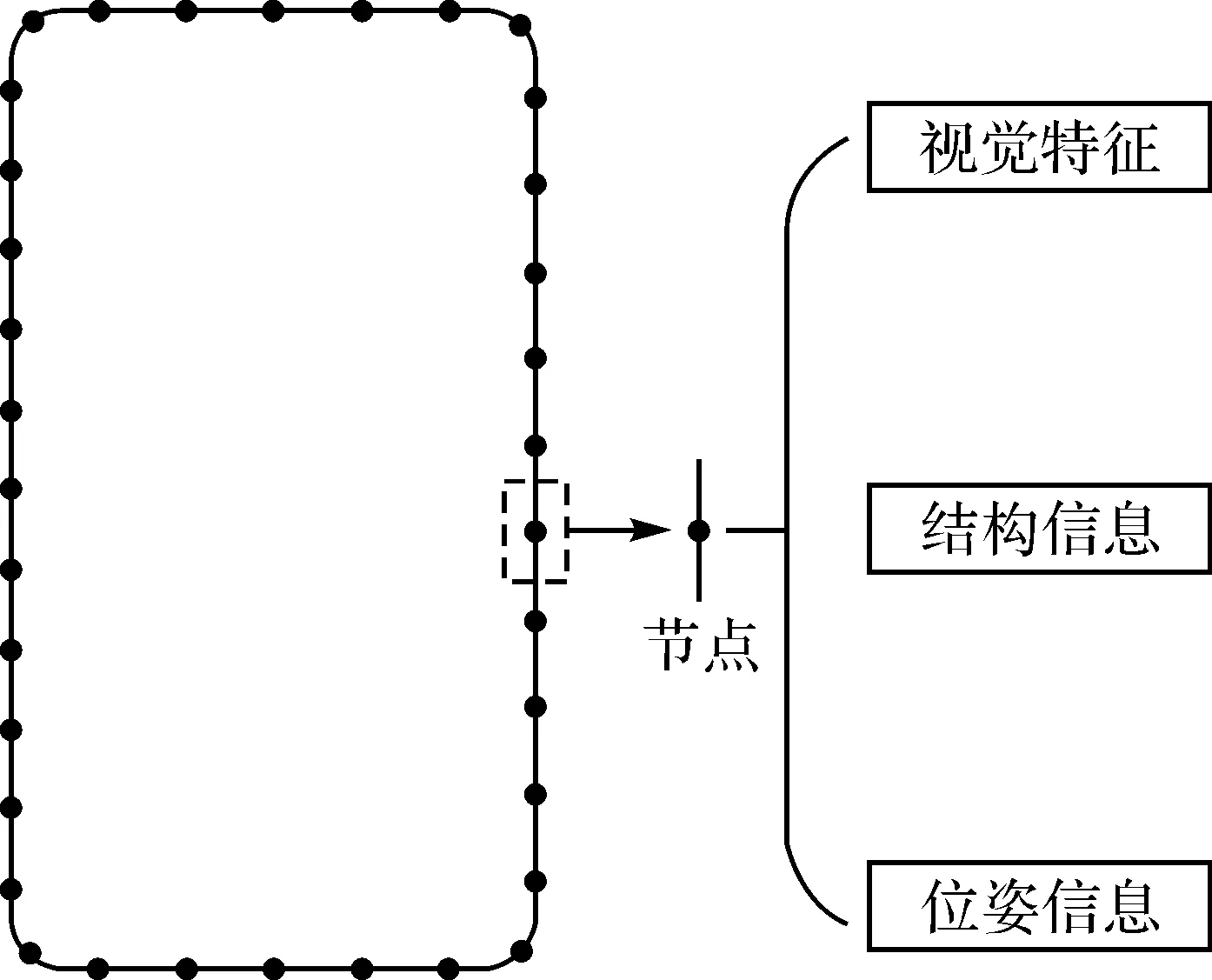
图1 环视特征地图示意Fig.1 Illustration of visual feature map from around view

本文利用现有的车载环视系统作为唯一的环境感知传感器。一方面，可以覆盖车辆周围360°的场景，大幅提高车辆的感知范围；另一方面，不需要增加额外的硬件设备即可实现车辆在GPS盲区环境中的高精度定位。由于鱼眼相机获取的图像存在较大的畸变，当距离车辆较远时，图像存在较大的失真，故感兴趣区域选择为车辆周围2～3 m的范围。为了避免前、后车辆及对向车道车辆的影响，本文根据相邻节点之间的距离，选取车辆右侧的区域为感兴趣区域，并提取该区域视觉特征，包括局部ORB特征[13]和全局ORB特征[21]。结构信息是指图像坐标系和全局坐标系之间的变换关系，可由式(2)表示，位姿信息存储车辆在全局坐标系中的位置[xmym]T(前轴中心的全局坐标)和姿态θ，可以将环视图像中的车辆位置映射为全局坐标

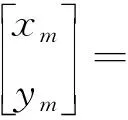
(2)

式中，[umvm]T为制图时车辆前轴中心的图像坐标；车辆位姿信息由高精度惯导获得，尺度因子λ通过系统标定得到；Rw和tw为要求的图像坐标系与全局坐标系之间的映射关系。

1.2 基于二阶MM-PF的智能车定位方法

针对室内环境中智能车无法有效利用GPS信号进行车辆定位，本文提出一种基于二阶MM-PF的地下停车场定位方法。该方法在环视地图构建的基础上，通过获取的环视图像，实现智能车高精度定位，算法流程如图2所示。首先，利用环视地图节点之间的拓扑关系，提出基于二阶MM的粒子状态转移模型。然后，提取当前图像的ORB全局特征，并与环视特征地图节点中存储的ORB全局特征进行比较，通过构建基于高斯分布的观测概率模型，计算各粒子的权重分布，根据粒子权重重采样，获得最佳节点级定位。最后，利用局部视觉特征匹配，计算当前车辆与地图中车辆的相对位姿，进而求得当前车辆在全局坐标系中的位置。

图2 基于二阶MM-PF的定位流程Fig.2 Visual map localization based on second-order MM-PF from around view

1.2.1 基于二阶MM-PF的节点级定位模型构建

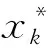
(3)

为了解决最优匹配问题，本文提出基于二阶MM-PF的环视特征地图定位算法来实现地图最优节点匹配，如图3所示。在本文中，利用粒子在t-1、t时刻的状态对t+1时刻的状态进行预测，构建粒子状态转移模型。然后，提取当前图像的ORB全局特征与特征地图节点的ORB全局特征进行比较，并构建基于高斯分布的粒子权重分布模型，通过重要性采样将拓扑结构信息与视觉信息进行融合，以提高车辆的定位精度和稳定性。主要包括粒子初始化、粒子状态转移模型、基于关键粒子的权重更新与重采样和最优地图节点估计4个步骤。

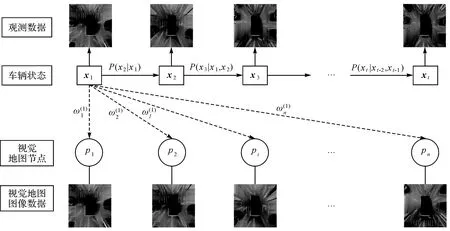
图3 基于二阶MM-PF的智能车环视地图匹配与定位Fig.3 Map matching and localization of intelligent vehicle based on second-order MM-PF

1.2.1.1 粒子初始化

(4)

(5)

1.2.1.2 基于二阶MM的粒子状态转移模型

在智能车定位中，控制量多为速度或加速度，而这些量的获取需要额外增加传感器，增加系统的使用成本。然而，在正常情况下，车辆的通行区域多为结构化的场景，在运动过程中，车辆状态具有一定的连续性。即下一时刻车辆的可到达区域与历史状态存在一定的关联关系。因此，为了适应不同的运动状态，并兼顾模型的复杂度，提出基于二阶MM的粒子状态转移模型，即t时刻粒子在空间中的分布情况取决于t-1和t-2两个时刻车辆的状态，如图4所示。假设车辆在短时间内速度不变，则有

(6)

式中，xj和xi分别为t-1和t-2时刻的状态；xk为t时刻车辆状态，则有

xk=2xj-xi+v(t)

(7)

式中，v(t)为状态转移过程噪声，其服从0均值高斯分布。状态转移利用历史状态提供的速度约束，确定粒子的状态转移关系。粒子分布如图4所示，×表示粒子与粒子分布情况。

图4 状态转移及粒子权重分布建模Fig.4 State transition and particle weight distribution modeling

1.2.1.3 基于关键粒子的权重更新与重采样

(8)

图5 全局ORB特征描述符Fig.5 Descriptor of ORB holistic feature

为了描述随着汉明距离的增加，观测概率逐渐变小这一现象，本文通过构建0均值高斯模型以构建观测图像与地图节点之间的相似度模型，并计算各粒子权重

(9)

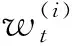
(10)

然而，随着迭代次数的增加，几乎所有粒子的权重都趋于0，粒子权重集中在少数粒子上，造成粒子枯竭，使PF退化，无法准确描述定位过程的不确定性。为了避免粒子枯竭造成PF性能恶化，在迭代若干次后，需要对粒子进行重分布。重分布可以增加粒子的多样性，更易适应复杂环境的状态估计。一种判断PF是否发生粒子枯竭的方法是比较PF的有效采样数

(11)

当Neff<2n/3时，需对PF进行重采样，n为粒子总数。

1.2.1.4 最优地图节点估计

根据当前状态获得的粒子权重，对粒子进行重采样。则当前车辆对应的地图节点为重采样后粒子数量最多的地图节点，即

(12)

式中，i表示第i个粒子；size(pi)表示重采样后粒子pi出现的次数。与传统粒子滤波算法相比，二阶MM-PF模型大大拓展了算法的适用性，简化了模型的复杂度，提高了定位的稳定性和精度。

1.2.2 基于局部特征匹配的度量级定位

在1.2.1节获得节点级定位后，利用局部ORB特征匹配，计算当前车辆与地图参考位置的相对位姿，得到当前车辆在全局坐标系中的位置。为了剔除错误的特征点匹配，本文利用RANSAC算法剔除错误的匹配特征点[22]，匹配效果如图6所示。当前图像和特征地图节点中存储图像之间的单应性可以由式(13)求得

(13)

式中，[umsvms1]T为环视特征地图节点中存储的特征点；[ucsvcs1]T为当前获取的环视图像的特征点；Hcm为当前图像与特征地图节点图像之间的单应矩阵。则当前车辆的全局坐标[xgyg]T可由图像坐标系与全局坐标系之间的映射关系Rw和tw求得，为

(14)

2 试验及结果分析

为了验证本文算法在实际场景中的性能，分别采集两个不同试验场景的数据进行验证。在试验之前，需要对车载广角鱼眼相机获取的原始图像(图7第1行)进行标定、畸变矫正(图7第2行)、视角变换(图7第3行)和拼接等处理。最后生成图像大小为416×416像素，如图7所示，具体过程不再赘述，见文献[23]。

图7 环视图生成过程Fig.7 Generating procedure of around view image

试验分别在两个地下停车场景环境中下进行，第1个场景为上海某汽车公司地下停车场，该停车场为单位自用，动态目标较少，场景面积约为10 000 m2。第2个场景为武汉某商场地下停车场，场景面积约为8000 m2，场景中存在车辆和行人等交通参与者，交通场景较为复杂，容易被动态目标遮挡，试验路段如图8所示。在室内环境中，车辆行驶速度有严格限制，试验过程中，车辆平均行驶速度均不超过20 km/h，所选地下停车场具有普适性。

环视特征地图采用文献[6,11]中的构建方法，首先，将待定位场景离散为一序列节点，采集各节点对应的路面结构信息、视觉特征和位姿信息等数据。视觉特征包括全局ORB特征和局部ORB特征。全局ORB特征的提取过程如1.2.1.3节所述，局部ORB特征为常规ORB特征。试验中，各摄像头采集图像的分辨率均为1280×960像素。试验在相同计算机硬件环境下运行，其配置为Intel Core i7-7700HQ 2.8 GHz CPU，8 GB RAM。为了比较不同算法之间的差异，选取基于BoW模型的定位算法[16]和基于PF多分辨率的定位算法[20]作为对比，进行试验。

2.1 工业园停车场场景测试

定位试验在已构建环视特征地图的地下停车场中进行，测试场景如图9所示，该场景环视特征地图节点数为164个，节点平均间隔为2 m。因地下停车场等结构化的场景有固定入口，首先，根据场景结构对系统位置初始化，并用环视特征地图中的节点信息初始化粒子。然后，根据车辆历史信息预测车辆下一时刻的状态。同时获取车辆当前时刻的图像信息，提取图像的ORB全局特征，利用式(8)计算当前图像的ORB全局特征与各粒子之间的汉明距离，并利用观测概率模型计算粒子权重分布。最后，根据粒子权重对粒子进行重采样，粒子数量最多的节点作为当前的定位结果。

试验结果的评价方法采用闭环检测中常用的衡量标准[24]，即当车辆在相邻节点之间时，通常认为最近的节点和次近的节点都是正确的匹配结果，即当误差帧等于0和等于1时，均认为是正确的匹配。试验中，误差帧是指试验获取的地图节点与真值之间的节点差。此外，为了更好地呈现试验结果，当节点误差大于等于5帧时，均按5帧处理。节点级定位的结果如图10所示。由图10可知，节点级定位误差集中在0帧和1帧，相较于对比算法，具有较好的稳定性和精度。

本文选择经典的BoW定位算法和多分辨率PF定位方法作为对比算法，其节点级定位的均值分别为0.13、0.39和0.37帧，误差均方差分别为0.65、1.25和1.18帧，成功匹配的概率分别为94.5%、82.9%和90.1%(表1)。从节点级定位的结果来看，仍存在误匹配的现象，主要是因为在地下停车场环境中，为了限制车辆的行驶速度而布设有减速带，当车辆通过减速带时，会引起车辆颠簸使视角变化较大，进而导致误匹配。然而匹配误差均小于3帧，这也说明了本文提出的二阶MM-PF的匹配方法能够将车辆的运动信息和视觉信息相融合，提高地图匹配的成功率。

在获得与当前图像最佳匹配的地图节点后，利1.2.2节介绍的图像特征点匹配方法，计算当前车辆与地图中参考坐标的相对位置，通过式(14)求得当前车辆在全局坐标系下的位置，试验结果如图11所示。 定位轨迹中由方框标注的定位波动较大，其原因是减速带或门槛的存在导致定位误差较大，也进一步说明了减速带或门槛导致节点级定位误差较大。

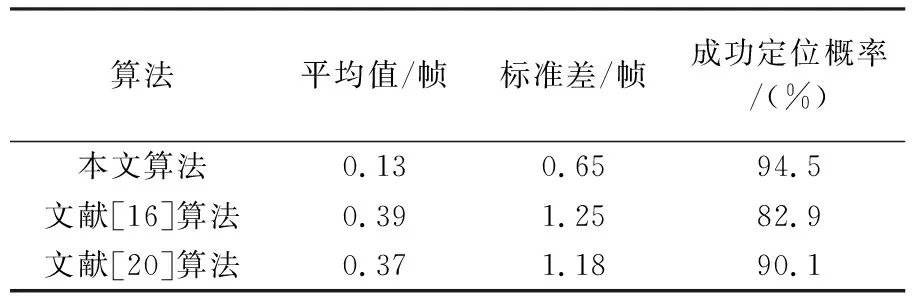
表1 不同算法在工业园地下停车场场景的节点级定位对比

统计结果见表2，定位平均误差为0.36 m，误差均方差为0.25 m。此外，与对比算法的程序耗时26.0 ms和98.3 ms相比，本文研究的平均耗时为15.6 ms，大幅提升了计算效率，使得本文算法具有较好的实时性。较高的计算效率归因于利用全局图像描述符来计算发射概率。一方面可以直接提取图像中心的描述符，省去特征点提取过程，一副图像由一个ORB描述符来描述，大幅简化匹配耗时。另一方面利用运动约束缩小地图匹配范围，并通过选取关键粒子减少重采样过程的计算耗时。由表2可知，定位误差小于1 m的概率为97.9%，试验结果也验证了本文算法具有较好的定位性能。

图8 测试路段Fig.8 Testing routes

图9 工业园停车场测试场景Fig.9 Scenarios of test route in parking lots in industrial park

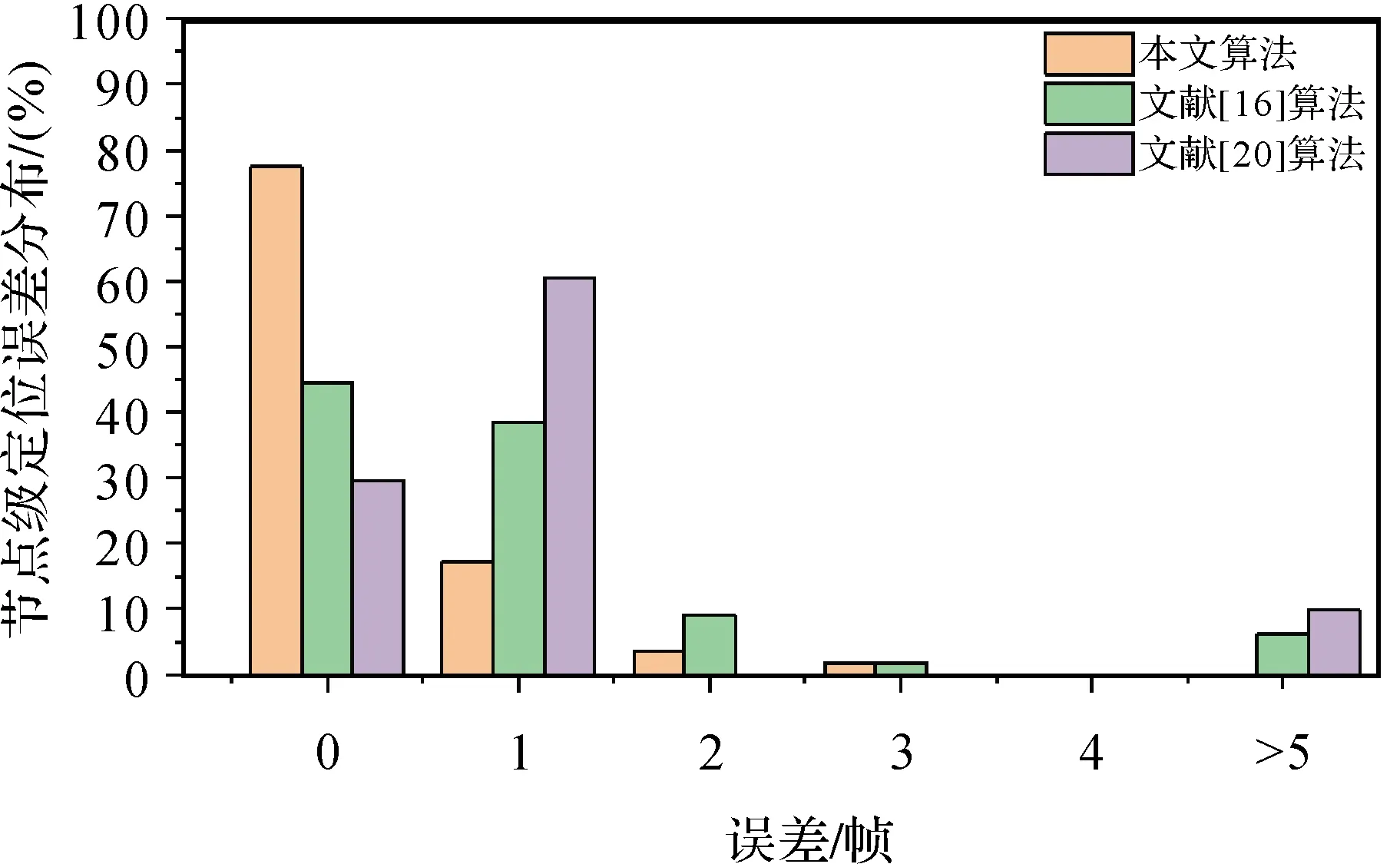
图10 工业园地下停车场节点级定位误差概率分布Fig.10 Error distribution of node-level localization in underground parking lots in industrial park

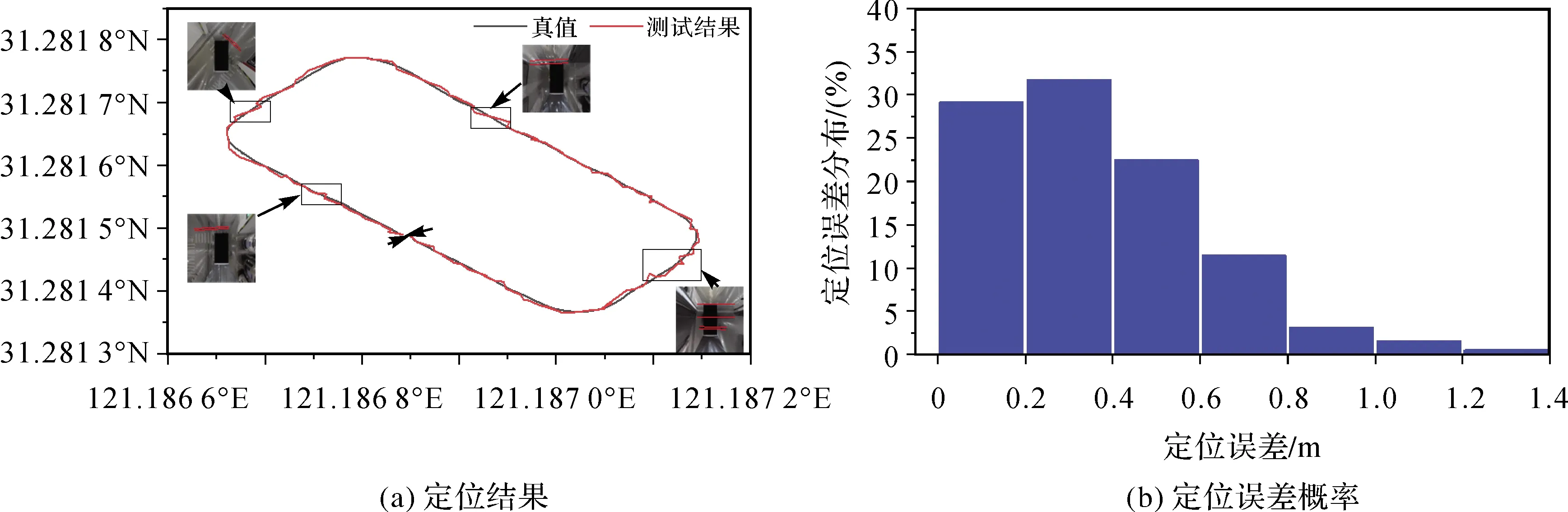
图11 定位结果Fig.11 Localization results

2.2 商场地下停车场场景测试

为了验证本文算法对不同场景的适应性，另外采集武汉某商场地下停车场数据进行验证，测试场景如图12所示。该测试场景环视特征地图节点数为135个，节点平均间隔为2 m。该地下停车场环境中存在移动的车辆和行人。

在商场地下停车场环境中，测试结果的误差概率分布如图13所示。由图13可以看出，此停车场环境下的地图匹配结果与2.1节工业园停车场测试结果具有相似的效果，地图匹配成功的概率为94.1%。该场景下，本文算法与对比算法的性能比较见表3，其中本文算法的平均节点级定位误差为0.10帧，误差均方差为0.60帧，试验匹配准确度和耗时均优于对比算法。由上述数据可知，本文提出的二阶MM-PF定位方法，在不同场景中具有稳定的地图匹配结果。

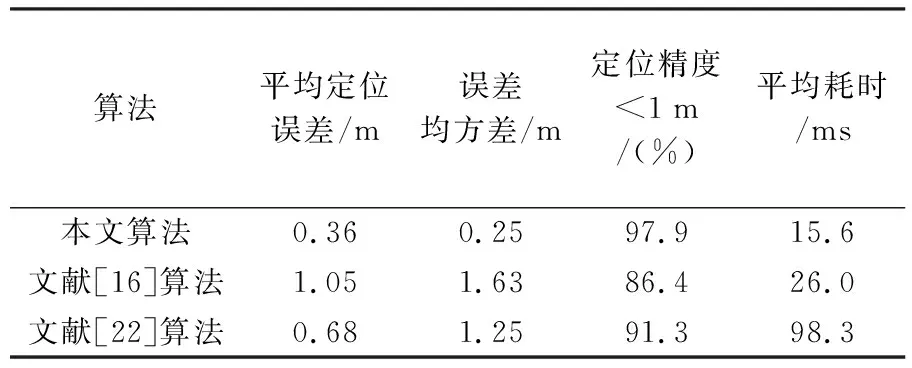
表2 不同算法在工业园地下停车场场景的度量级定位对比

图12 商场停车场环境Fig.12 Scenarios of mall parking lots

表3 不同算法在商场地下停车场的节点级定位对比

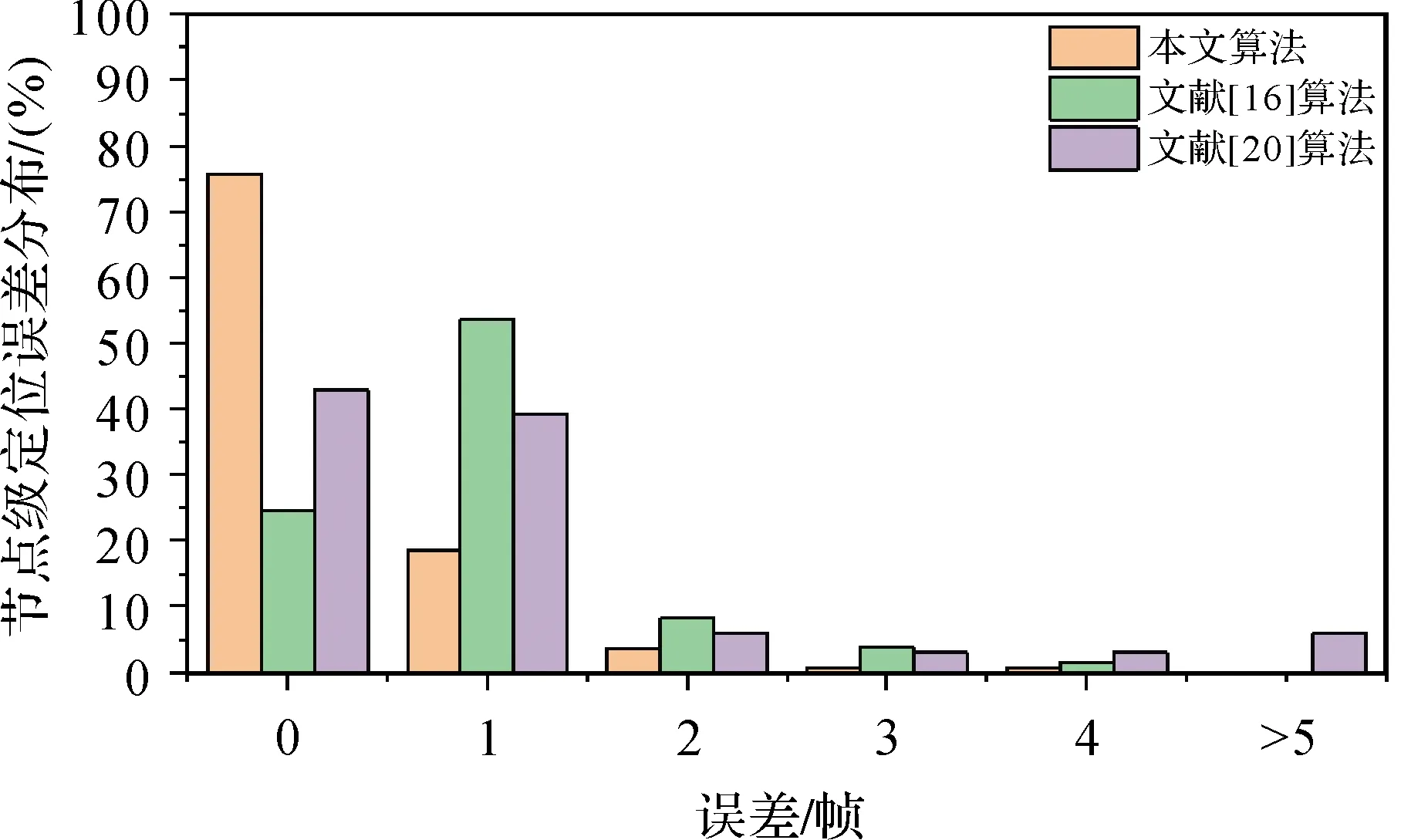
图13 商场地下停车场节点级定位误差概率分布Fig.13 Error distribution of node-level localization in underground parking lots shopping malls

在该场景中，车辆在全局坐标系中的定位结果如图14所示，其平均定位误差为0.38 m，误差均方差为0.29 m，其定位误差小于1 m的概率为95.4%，本文算法与对比算法的定位结果见表4。由图14可知，动态目标的存在恶化了系统的定位性能，然而，在车辆运动的约束下，其定位误差不会出现较大的波动。说明本文算法对存在动态目标的场景也具有较好的定位精度和稳定性。这也进一步说明了本文算法在不同场景中的有效性。

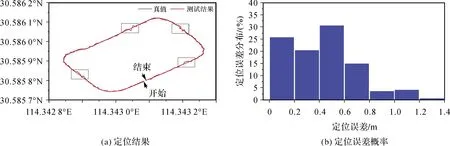
图14 商场地下停车场定位结果Fig.14 The results of localization in the underground parking of mall

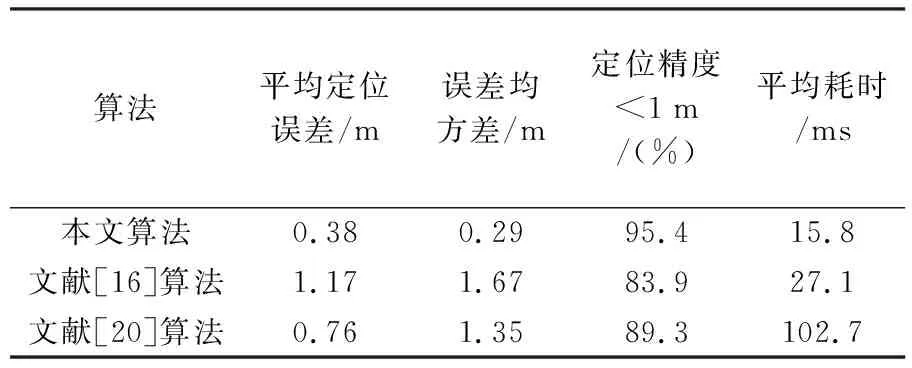
表4 不同算法在商场地下停车场的度量级定位对比

3 结 论

针对地下停车场环境中GPS定位精度较低，本文利用环视图像构建地下停车场场景的环视特征地图，并提出一种基于二阶马尔可夫模型与粒子滤波算法相结合的节点级定位方法。在定位过程中，该方法仅利用车辆自身配备的环视系统即可实现车辆的高精度定位，大幅降低了车辆的定位成本，并在不同的场景中对所提算法进行验证，可以得出以下结论：

(1) 本文算法在不同场景中的平均定位误差不超过0.38 m，定位误差均方差小于0.29 m，定位误差在1 m以内的概率不低于95.4%，试验结果表明，利用所提出的二阶MM-PF定位方法可有效地提高定位精度。

(2) 通过获取关键粒子，平均定位耗时在16 ms以内，均优于对比算法，说明本文算法具有较高的定位效率，能够满足智能车实时定位的需求。

(3) 在两个不同的地下停车场环境中，对所提出的算法进行验证，能够获得相近的定位结果，证明本文算法仅利用车辆自身搭载的环视系统即可实现稳健的定位效果。