设置黏滞阻尼器的超高墩大跨铁路连续钢桁梁桥纵向减震性能研究

2021-12-09邵长江漆启明王应良戴晓春

中国铁道科学 2021年6期

邵长江，漆启明，韦旺，王应良，戴晓春，黄辉

（1.西南交通大学土木工程学院，四川成都 610031；2.中铁国际集团有限公司，北京 100039；3.中铁二院工程集团有限责任公司，四川成都 610031）

西部山区地质复杂，且多为深沟峡谷，高墩大跨桥梁是此类地区铁路工程建设的优选桥型［1］。在此，借鉴民用建筑规范规定，建筑高度大于100 m 为超高层建筑［2］，将100 m 以上的桥墩界定为超高墩。由于艰险山区（如汶川、玉树及芦山等）大多地震频发，高烈度区超高墩大跨桥梁的抗震设计显得尤为重要。然而，现行GB 50111—2006《铁路工程抗震设计规范》［3］仅涉及中低墩的延性验算，JTG/T 2231-01—2020《公路桥梁抗震设计规范》［4］相关条文主要面向采用减隔震支座的常规桥梁，这给超高墩大跨铁路桥梁的减隔震设计带来挑战。

相对于中低墩常规桥梁，超高墩大跨桥梁属于长周期结构，采用附加耗能装置比延长周期的隔震支座更为合适［5］。黏滞阻尼器因兼具减震、限位双重功效，备受设计人员青睐，已在各类桥型中广泛应用［6］。毛玉东等［7］和李晓波［8］通过比较黏滞阻尼器和双曲面减隔震支座下的纵向减震机理和减震效果，分别给出了公路和铁路大跨混凝土连续梁桥的合理抗震设计建议；马安财等［9］针对跨海桥梁建立了考虑动水压力的连续梁简化模型，提出了优化黏滞阻尼器参数的Lyapunov 方法；焦驰宇等［10］将黏滞阻尼器应用于市政桥梁抗震加固，其较常规加固方案在工程造价、交通影响、可实施性等方面更有优势；苗润池［11］通过在桥塔和加劲梁间设置黏滞阻尼器的大跨悬索桥减震研究，发现阻尼器可大幅度减小加劲梁位移，但对塔底内力的减震效果并不明显；Xu等［12］采用响应面法对大跨斜拉桥的阻尼器参数进行优化，并通过全桥振动台试验验证了所提优化算法。

上述成果为中低墩连续梁桥和大跨缆索桥的减震设计提供了有力支撑，但针对超高墩大跨桥梁的研究较少。张育智［13］提出了在主梁与桥台间设置黏滞阻尼器的摇摆自复位高墩隔震体系；刘尊稳等［14］以某铁路高墩大跨刚构-连续梁桥为例探讨了在桥台和活动墩上设置阻尼器的减震效果。以上两者并未研究超高墩墩梁间设置阻尼器的减震行为。另外，相比中低墩，超高墩较柔，且自身质量较大，墩身惯性力大，加之高阶振型的影响，上部结构产生的墩身内力对其总体响应不再起到控制作用，且在相同频段范围内振型更密集、质量参与系数更高［15］，但高阶振型对超高墩桥梁的阻尼器减震规律影响研究鲜有报道。

本文以某超高墩大跨连续钢桁梁桥为例，研究设置不同参数黏滞阻尼器的超高墩大跨连续钢桁梁桥纵向减震规律，通过墩高变化探明高阶振型对高墩阻尼器减震性能的影响，提出超高墩大跨桥梁的抗震设计建议。

1 桥梁结构

某铁路特大桥的总体布置如图1 所示，跨径为（38.6+108+151.5+249+151.5+108+25.6）m，桥梁全长832.2 m，主桥为5 跨1 联的上承式连续钢桁梁，左右分别为2跨和1跨的圬工拱桥引桥。大桥采用双线高速铁路技术标准，线间间距为4.2 m。主梁为变高度钢桁架梁，等高段桁高16.0 m，中支点处桁高36.0 m，按二次抛物线变化；大桥采用球钢支座，仅中墩P2 为固定墩，其余均为活动墩台，支座及黏滞阻尼器布置方案如图2所示。

图2 支座及黏滞阻尼器布置

特大桥T0 和T5 桥台采用拱式桥台，P1—P4桥墩采用钢-混组合钢架墩，墩高依次为51，139，154 和67 m。墩身由2 个“D”形薄壁空心截面组成，2 个“D”形墩之间沿竖向每隔15 m 设置1 对“X”钢横撑，如图3 所示，其中P1—P4 桥墩所设钢横撑数量分别为2 对、8对、9对和3对。桥面系采用的是正交异性钢桥面，如图4所示。

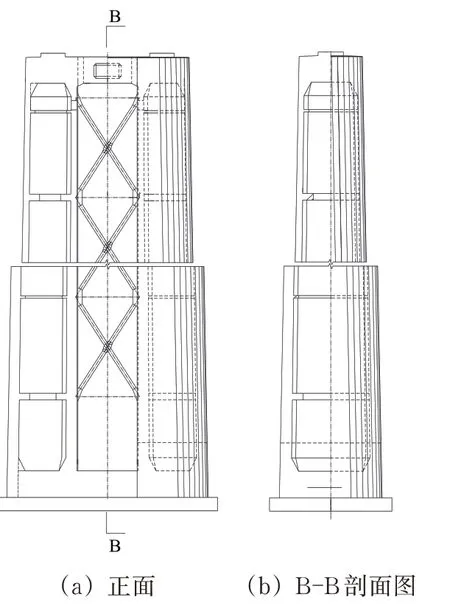
图3 桥墩构造示意图

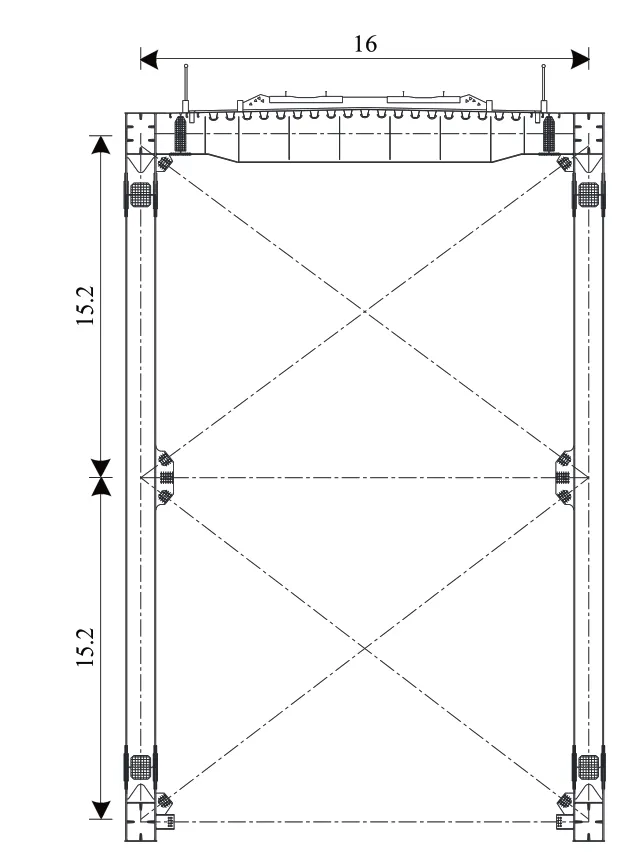
图4 主梁构造示意图（单位：m）

2 有限元模型及地震动参数

基于SAP2000 软件建立桥梁空间有限元模型，如图5所示。钢桁架梁、桥墩、承台及双肢墩柱间的“X”撑均采用梁单元模拟，正交异性钢桥面等效为板单元。球形钢支座通过双线性理想弹塑性恢复力模型模拟，黏滞阻尼器通过Maxwell 模型模拟。

图5 桥梁空间有限元模型

结合地勘数据和TB 10093—2017《铁路桥涵地基和基础设计规范》［16］，采用m 法考虑桩-土-结构相互作用。恒载主要包括结构自重和二期铺装，顺桥向不计算活载引起的地震力。根据桥址的场地地震安全评价报告，本桥梁桥址场地为中硬土，特征周期为0.45 s。罕遇地震PGA为0.227g（g为重力加速度），加速度反应谱（阻尼比5%）和加速度时程曲线如图6和图7所示。

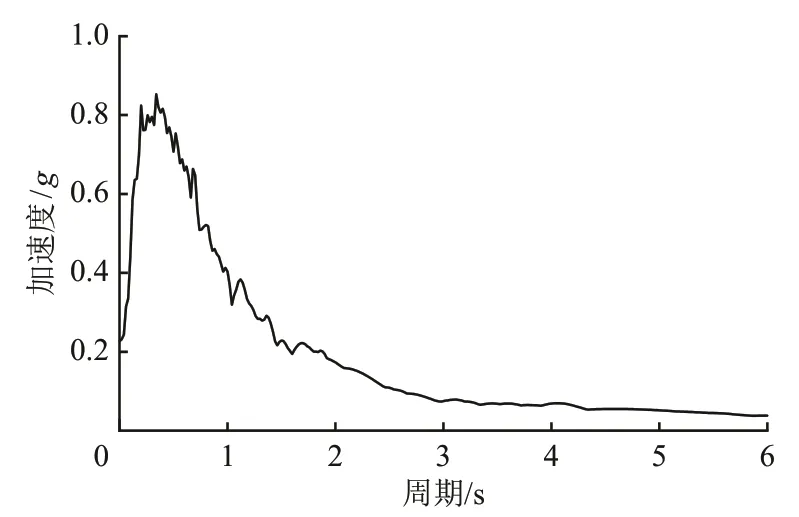
图6 罕遇地震加速度反应谱

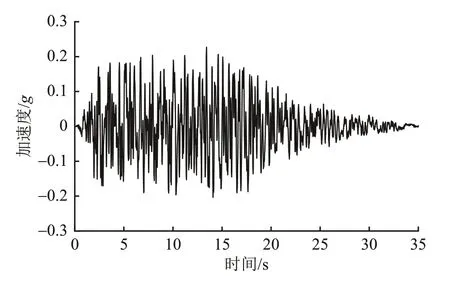
图7 罕遇地震加速度时程曲线

3 结构动力特性

准确把握桥梁结构的动力特性是进行抗震性能分析的必要环节。下文重点研究该铁路特大桥的纵向减震性能，因此仅给出纵桥向质量参与系数随振型序号的变化，如图8所示。图中：Ti为第i阶振型周期。通过查阅质量参与系数较大的序号，发现其对应振型均为桥墩纵向弯曲振型，结果汇总见表1。

图8 纵桥向质量参与系数

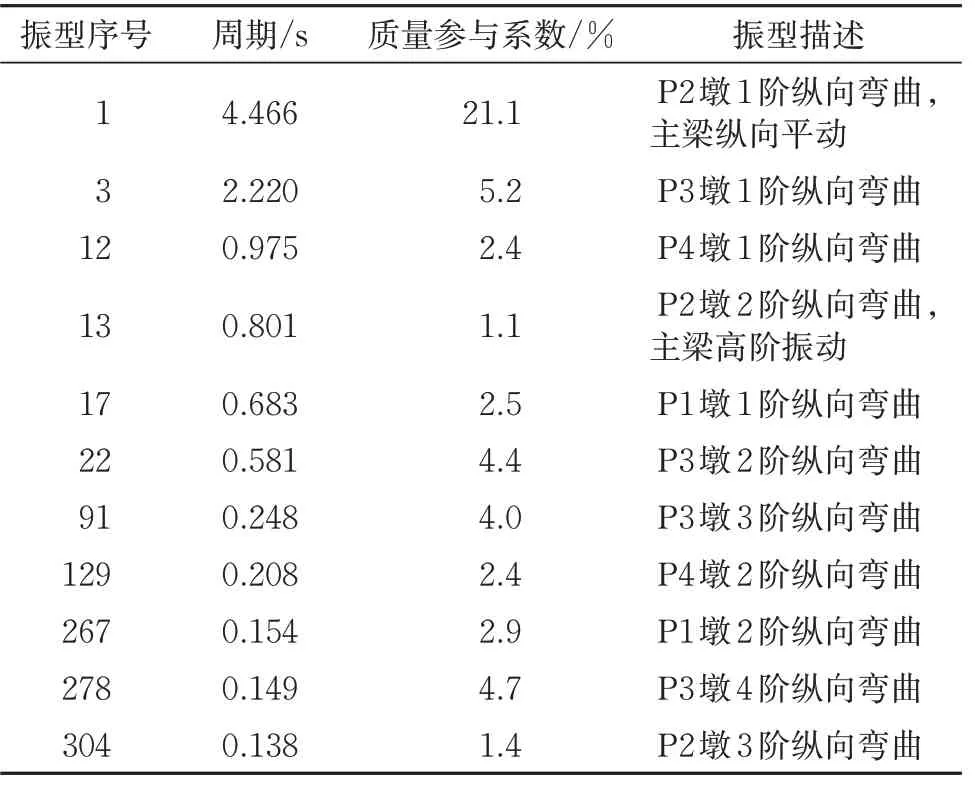
表1 桥梁各墩的纵向典型振型

由图8 及表1 可见：超高墩大跨连续钢桁梁桥的1 阶周期为4.466 s，P2 墩身纵桥向第1 阶振型质量参与系数仅为21.1%，该桥属于长周期的非规则桥梁；前30 阶振型纵向累积质量参与系数仅为40.77%，到第494 阶时纵向累积质量参与系数才超过90%，结构振型复杂；上部结构振型的纵向质量参与系数均较低，且分布较广；对于活动墩P1（高51 m）、P4（高67 m）和P3（高154 m），墩身1阶纵向弯曲周期随墩高依次增大，表明超高墩相对更柔；高阶振型中，桥墩纵向质量参与系数较大，P2 和P3 这2 个超高墩的3 阶纵向弯曲所占的纵向质量参与系数仍较高；表1中各桥墩累计质量参与系数已达52.1%，可见当桥梁受到强烈地震激励时，超高墩身有可能激发出很多高阶振型，这与中低墩桥梁动力特性相比是截然不同的。因此，进行超高墩桥梁地震响应计算时，不能忽略高阶振型的影响。

4 黏滞阻尼器参数对减震的影响

黏滞阻尼器的阻尼力FD与阻尼系数C、阻尼器活塞相对缸体的运动速度v及速度指数α相关。桥梁抗震领域中，常用速度指数值一般取0.3～1.0［6］。桥梁各位置阻尼器均采用相同型号，优化时阻尼系数C取值范围为2 000～6 000 kN ·（m·s-1）-α，速度指数α取值范围为0.2～0.8，总计25个工况。

黏滞阻尼器的主要功效是增强结构阻尼，强震下对结构起到耗能、限位作用，因此主要控制指标为位移响应，次要控制指标为内力响应。阻尼器优化控制指标：①主梁梁端、墩顶以及支座位移；②单肢“D”形墩墩底的弯矩、剪力。同时，做如下定义，减震率=（无阻尼器结构地震响应-设置阻尼器结构地震响应）/无阻尼器结构地震响应。

4.1 对位移响应的影响

图9—图11分别为地震作用下桥梁支座、梁端及墩顶的纵向位移随阻尼器参数的变化曲线。

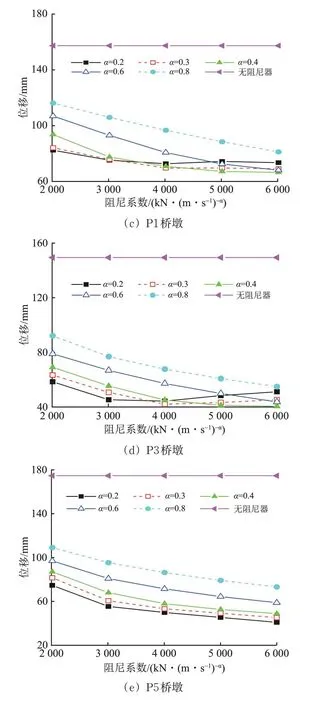
图9 支座纵向位移随阻尼器参数的变化

图10 梁端纵向位移随阻尼器参数的变化

图11 墩顶纵向位移随阻尼器参数的变化

由图9 和图10 可见：当阻尼器速度指数α一定时（除α=0.2），支座纵向位移随阻尼系数C的增大而减小，但α为0.2 和0.3 时桥台支座和梁端位移出现先减小后增大，表明α不宜过小或过大；当C一定时，支座和梁端位移响应整体上随α的提升而增大。

由图11可见：同一速度指数下，P1和P2桥墩墩顶位移随着阻尼系数的增加近似呈线性增长，但P2 桥墩在部分工况下的墩顶位移已超过未设阻尼器时；P1 和P2 桥墩在同一阻尼系数时的墩顶位移随α的增加而减小；超高墩P2的墩顶位移响应在α为0.3 和0.4 时出现最低点，在速度指数最小（0.2）和较大（0.6 和0.8）时分别线性增加或减小，而超高墩P3 的墩顶位移随α变化相对较小。总体来看，黏滞阻尼器对桥梁的支座、梁端和墩顶位移的减震效果非常明显。

4.2 对内力响应的影响

图12 和图13 分别为墩底剪力和弯矩随阻尼器参数变化的曲线。根据既有空心墩试验成果［17］，取桥墩右肢墩底空心倒角上缘作为内力输出截面。

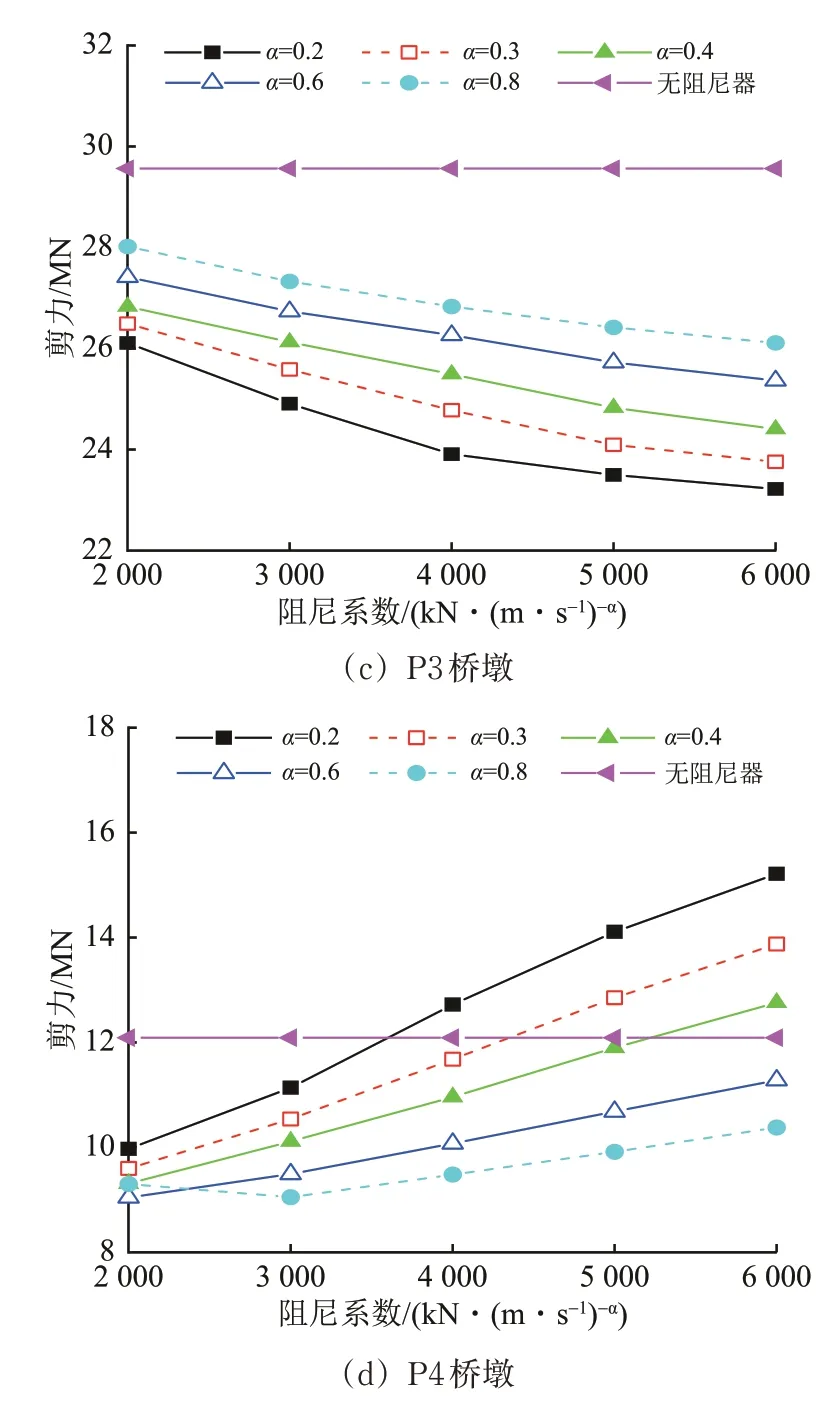
图12 墩底剪力随阻尼器参数的变化

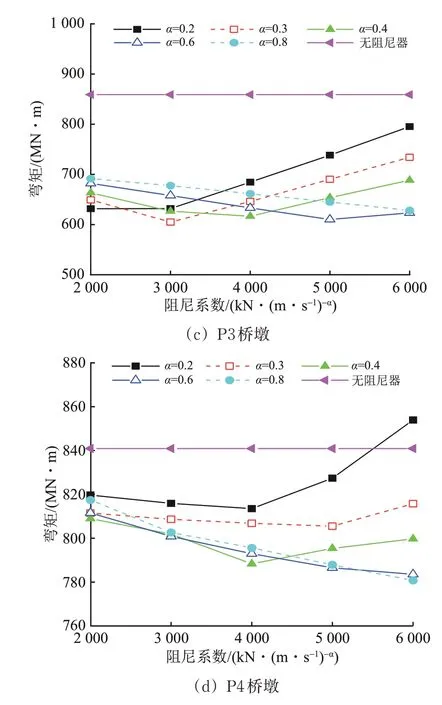
图13 墩底弯矩随阻尼器参数的变化

由图12和图13可见：除P1桥墩外，其余桥墩的墩底剪力随阻尼系数呈单调趋势变化，其中固定墩P2 和活动墩P4 为上升趋势，活动墩P3 为下降趋势；当阻尼系数一定时，桥墩P2 和P4 的墩底剪力随速度指数的增加而减小，活动超高墩P3 的趋势则恰好与之相反；桥墩P1 和P2 的墩底弯矩变化趋势接近，均随阻尼系数呈正相关，随速度指数呈负相关；桥墩P1 的墩底剪力及P3 和P4 的墩底弯矩在部分速度指数下出现了先减小后增大的趋势，这是阻尼器参数优化时需关注的重点，不合理的阻尼器参数会加剧地震响应；P2 墩底剪力在各工况下均大于未设阻尼器的响应，但其墩底弯矩在阻尼器工况下明显减小，说明墩底剪力和弯矩的变化规律并非一致，该现象将在后文结合墩身内力包络及高阶振型影响予以阐释。综合考虑桥梁结构的位移、内力响应及阻尼器安装制作成本，建议阻尼器速度指数α取0.4，阻尼系数C取3 000 kN·（m·s-1）-0.4。

4.3 对减震效果的影响

运用已建的桥梁有限元模型，进行最终选定的阻尼器参数和无阻尼器条件下的时程分析计算结果对比分析，研究黏滞阻尼器的减震效果。

表2 为桥梁减震前后的支座位移和墩顶位移响应比较。

由表2 可见：无阻尼器时P1，P3 和P4 桥墩对应支座的最大地震位移依次为157.3，149.5 和174.6 mm，采用黏滞阻尼器后位移降为77.4，55.4和67.6 mm，减震率达到了50.8%，62.9%和61.3%，说明设置阻尼器能够大幅度减小各活动墩支座的位移响应，极大程度避免了主梁纵向碰撞和落梁等震害的发生；各墩的墩顶位移幅值也有不同程度的降低，无阻尼器时P1，P2，P3和P4桥墩的墩顶最大位移分别为73.4，128.5，153.6 和88.6 mm，与墩高变化趋势一致，而采用黏滞阻尼器后桥墩的减震率为28.4%， 31.9%， 14.2% 和24.0%。

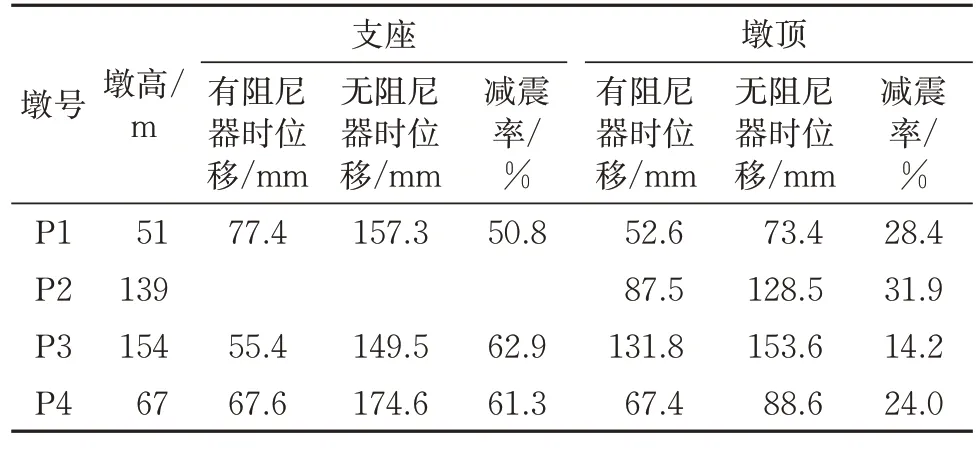
表2 桥梁支座位移、墩顶位移响应及减震率

图14 为地震作用下活动超高墩P3 的黏滞阻尼器及支座位移滞回曲线。由图14 可见：阻尼器滞回环近似椭圆且较为饱满，而盆式支座的滞回环面积明显减小，说明黏滞阻尼器耗散了地震能量并发挥了纵向限位作用。

图14 P3桥墩墩顶黏滞阻尼器及球钢支座滞回曲线

图15 为2 个超高墩减震前后的墩顶位移时程曲线。由图15 可见：固定墩P2 的峰值位移相对活动墩P3 的降幅更大，2 个桥墩在计算时间步约22～32 s时的减震也非常明显。

表3 为桥梁减震前后墩底内力响应比较。由表3 中的内力响应可见：P1（墩高51 m）和P4（墩高67 m）桥墩的墩底剪力和弯矩均较大程度地减小，减震率在26.5%～37.3%之间，极大缓解了对P1 和P4 桥墩桩基础的压力，且2 个边墩的墩底内力与墩顶位移的减震率较接近。

表3 桥梁墩底剪力、弯剪的响应及减震率

尽管固定超高墩P2 减震后的墩顶位移仅为87.9 mm，位移减震率达到31.9%，弯矩减震率为27.0%，但其墩底的剪力反而比基准模型放大了4.5%，凸显了墩底剪力响应规律的不一性。对于活动超高墩P3，其墩顶位移减震率为14.2%，墩底剪力减震率为11.6%，但墩底弯矩减震率仅为4.6%，相比前两者的减震率差异较大。

图16为超高墩P2和P3墩底弯矩时程曲线。由图16 可见：各计算时间步的墩底弯矩减震效果均不如图15中的墩顶位移响应显著。

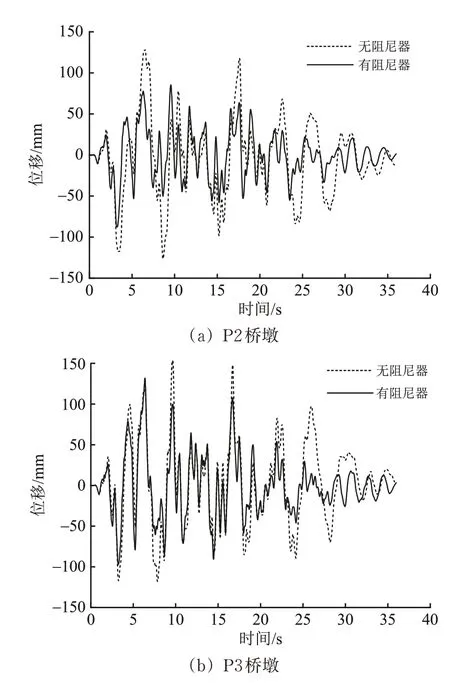
图15 P2和P3桥墩的墩顶位移时程曲线比较

图16 P2和P3的墩底弯矩时程曲线比较

由上可知，超高墩P2 和P3 桥墩的墩顶位移和墩底内力减震率差异显著，与高墩P1 和P4 的减震行为存在一定差异，相比中低墩减震规律［7-10］的一般认识有所不同。

究其缘由（见表1），超高墩连续钢桁梁桥振型1（P2 的1 阶纵向弯曲+主梁纵向平动）的质量参与系数仅为21.1%，上部结构质量不再对超高墩的地震响应起主控作用。P2 桥墩在振型13 发生2 阶纵向弯曲（质量参与系数为1.1%），P3 在振型22，91 和278 分别出现2 阶、3 阶、4 阶纵向弯曲，质量参与系数依次为4.4%，4.0%和4.7%，正是这些高阶振型使得超高墩的减震行为不同于中低墩。为进一步明确高阶振型影响，分别将有无阻尼器模型的墩高等比例降低，对比墩P2 和P3 的典型振型及质量参与系数，研究各墩高模型的黏滞阻尼器减震规律。

5 高阶振型对高墩阻尼器减震性能影响

考虑到4个桥墩的高度不一，“X”横撑数量分别为2，8，9 和3 个，故以8 个“X”撑的固定墩P2为基准，超高墩P2和P3依次逐个减少X撑数量（每个X 撑15 m），而高墩P1 和P4 根据固定墩P2依次等比例分别减小5.5 和7.2 m。由于P2 和P3桥墩墩高远大于P1、P4 桥墩，故仅选取P2 和P3桥墩的动力特性及位移、剪力、弯矩响应进行比较。

5.1 结构振型

表4 为不同墩高桥梁模型的P2 和P3 桥墩典型振型比较。

由表4 可见：随着墩高的减小，固定墩P2 桥墩的1阶纵向弯曲周期和相应质量参与系数均逐渐减小，在64 和49 m 高度时，P2 桥墩的1 阶纵向弯曲由第1 振型变化为第2 振型。P2 桥墩的2 阶纵向弯曲首次出现在第13 振型，随着墩高降低，其2阶弯曲振型出现更为靠后，对应的振型编号依次为25，28 和44，周期由第13 振型的0.80 s 下降到第44振型的0.32 s，94 m 墩高后不再出现2阶纵向弯曲；与P2 桥墩类似，活动墩P3 的1 阶纵向弯曲周期随着墩高的减小而降低，出现位置由原墩高（154 m）的第3 振型变化至64 m 墩高时的第12 振型，周期亦从2.22 s 下降至0.67 s；与固定墩P2不同的是，活动墩P3的2阶纵向弯曲和3阶纵向弯曲振型在桥墩降低为一般高墩仍会出现，活动墩P3 的2 阶弯曲振型由154 m 的第22 振型变化为64 m时的第185振型，周期由0.58 s减至0.19 s；3阶纵向弯曲由原P3桥墩的振型91变化为79 m时的第315 振型，周期由0.25 s 降至0.13 s；P3 桥墩在各高度的2 阶和3 阶弯曲振型仍有较大的质量参与系数（均超过4.7%）。总体来看，高墩和超高墩均可能在地震下出现高阶振型，且活动高墩相对固定高墩更容易激励出更多高阶振型。

表4 不同高度P2和P3桥墩的纵向典型振型比较

5.2 剪力响应

图17 为地震作用下不同墩高的墩身剪力包络分布（黏滞阻尼器简称FVD）。对于固定墩P2 而言，墩身剪力包络总体上呈现“两头大、中间小”的分布，上部剪力大的原因主要是P2 桥墩墩顶与主梁纵向约束，来自梁体的惯性力大部分直接传递至墩身上部；墩底剪力大的原因源于墩身和梁体的共同作用，主要对应桥墩的1阶纵向弯曲；由于高阶振型的影响，特别是桥墩2 阶纵向弯曲振型，桥墩中部的剪力反而相对两端更小；随着墩高减小，高阶振型参与程度降低，当墩高49 m 时，墩身剪力趋于线性，甚至出现桥墩中部剪力更大的情况。设置阻尼器适当增加了原P2 桥墩距承台40 m 范围内的剪力需求，但墩身其余区域剪力均优于不设阻尼器工况；随着墩高降低，高阶振型影响减弱，采用阻尼器后的墩身剪力需求均小于不设阻尼器的模型；特别是P2 桥墩墩高降低至49 m 时，虽未调整至最优阻尼参数，但剪力需求沿墩身的减震率范围为23.4%～36.9%，有效改善了固定墩的纵向受力。

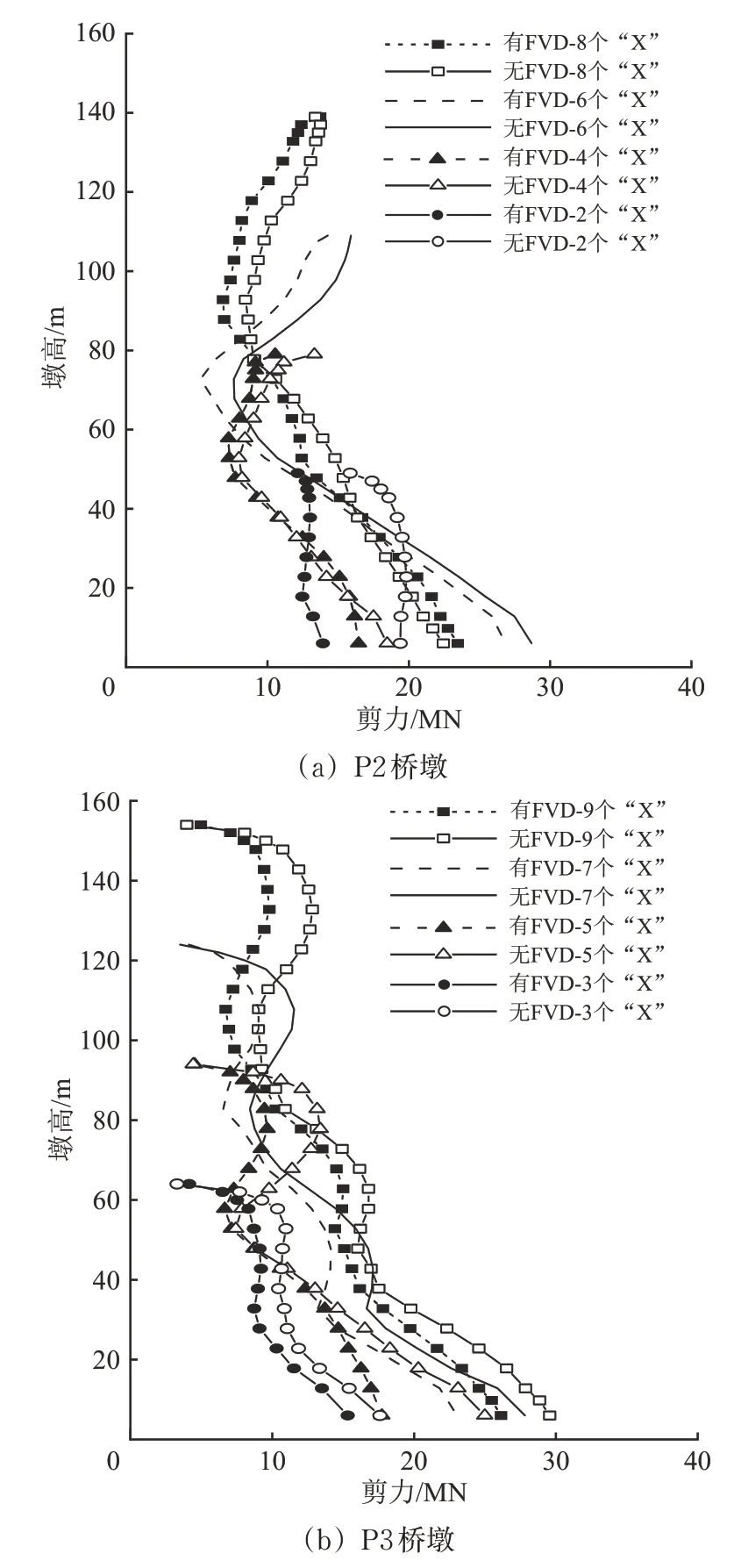
图17 P2和P3墩身剪力包络比较

对于活动墩P3 而言，墩身剪力包络曲线分布更为复杂，154 和124 m 的桥墩出现了4 个拐点，94 和64m 的桥墩也出现了2 个拐点，主要原因是P3 桥墩为活动墩，墩梁间的约束相对较弱，P3 桥墩在地震作用下激励出更多高阶振型，且这些振型的质量参与系数较大，即体现为墩身剪力分布；不同于P2 桥墩，设置阻尼器后P3 桥墩在不同墩高且沿整个墩身的剪力需求均更小，特别是94 m 墩高时的墩底剪力响应降幅高达29.0%。

5.3 弯矩响应

图18 为地震作用下不同墩高的墩身弯矩包络。与剪力不同的是，墩身的弯矩与距墩顶的距离有关。弯矩在墩顶位置最小，在墩底达到最大，这与普通中低墩桥梁一致，但因高阶振型影响，超高墩的墩身中部弯矩分布相比中低墩差异较大。

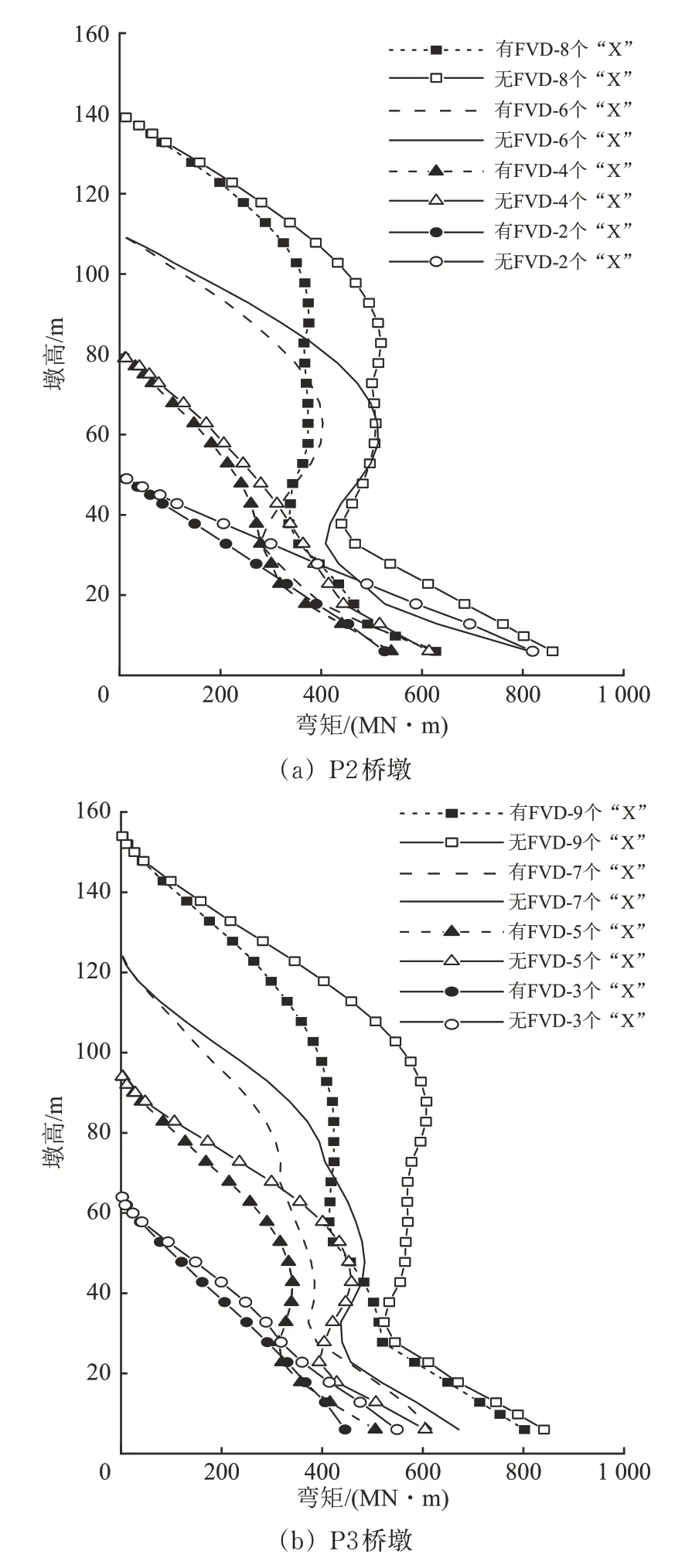
图18 P2和P3墩身弯矩包络比较

固定墩P2在139和109 m高度时弯矩包络线出现了2个拐点；原型P2桥墩在中部1/3区域的弯矩包络值接近，近似竖向直线分布，而在该区域之上和之下的弯矩随着高墩呈单调变化；109 m 固定墩弯矩包络呈“S”型，基准模型和减震模型距墩底约2/3 位置的弯矩分别为510 和400 MN·m，比1/3墩高处弯矩分别大44.8%和25.5%；但79 m固定墩弯矩分布已无明显拐点，当高度降至49 m 时，弯矩直接为线性，表明高阶振型影响逐渐削弱。采用黏滞阻尼器后，不同墩高P2 桥墩的墩身弯矩响应均显著减小，原超高墩P2 在40～100 m 范围减震率为18.9%～29.4%（平均约26%），尤其是降至49 m 时的墩底弯矩减震率高达35.8%，与墩底剪力减震规律一致，符合中低墩减震规律的认识。

活动墩P3 的弯矩变化规律与P2 桥墩较为接近，但由于墩梁之间约束更弱，加之其比P2 桥墩高15 m，非减震模型和减震模型在94 m 时的弯矩分布仍出现两个明显拐点，在桥墩47.8 m 处弯矩分别为380 和480 MN·m，比32.8 m 位置的弯矩大10.8%和3.4%。尽管原P3 桥墩在墩底的弯矩减震仅4.6%，但在40～120 m 高度范围内的弯矩响应明显得到降低，减震率为13.8%～31.4%（平均约27%）；P3 墩高降至124 和94 m 呈现近似规律，说明黏滞阻尼器能优化高墩的墩身弯矩分布。

原P2 和P3 桥墩在墩身中下部的弯矩包络相对中低墩更加外凸、饱满，即在靠近墩顶的区域仍有较大的弯矩，变截面墩身在中部相对于墩底的承载力面积减少幅度较大、轴压降低较快。因此，抗震验算时，除墩底外，墩身中部也需重点关注。