基于PCA-LSTM的轴承退化趋势预测
2021-12-09邵辰彤王景霖李胜男封锦琦
邵辰彤, 王景霖, 徐 智, 杨 乐, 李胜男, 封锦琦
(1.故障诊断与健康管理技术航空科技重点实验室,上海 201601; 2.航空工业北京长城测控技术研究所,北京 101111)
对于滚动轴承来说,高温、高压以及多变的负载情况是其常见的工作环境。因此,故障发生的频率也较高[1]。所以,通过分析滚动轴承的退化趋势并及时维修和更换不仅有利于工程设备的维护和保养,更能防止其故障发生后对其他部件带来的二次损害,在工程实际应用中具有重要意义[2]。
滚动轴承的退化趋势预测通过对运行中的轴承数据进行采集并预测轴承下一步的退化状态趋势,可以及时对轴承的可靠性做出有效判断并进行安全性维修,避免轴承超出使用寿命导致失效或未达到预期使用寿命导致成本增加[3]。轴承的退化趋势预测按照顺序基本可以分为以下几个部分:信号预处理、特征提取、趋势预测。在轴承振动信号的采集中由于存在噪声覆盖初始信号、传感器精度不足等问题,且振动信号往往呈现出非平稳非线性的状态,导致难以从中提取轴承故障特征,因此需要对轴承信号进行预处理。信号预处理中常用的方法有经验模态分解[4](Empirical Mode Decomposition,EMD)、奇异值分解[5](Singular Value Decomposition,SVD)、小波降噪[6]等,王奉涛等[7]使用EMD方法分析了滚动轴承的振动信号,并基于神经网络搭建了基于堆栈稀疏自编码器(Stacked Sparse Auto Encoder,SSAE)的故障诊断模型,简化了特征提取过程,提高了轴承的诊断正确率;胡晓依等[8]使用SVD剔除了轨迹矩阵中的噪声并使用STFT技术进行轴承信号的解调分析,结果表明,其能够更早一步发现轴承的早期故障。轴承信号的特征提取按照方法可分为时域指标特征提取、频域指标特征提取和时频域指标的特征提取[9]。轴承的退化趋势预测目前主要应用的是基于数据驱动的退化趋势预测方法,包括统计方法和人工智能预测方法。其中,统计方法包括自回归滑动平均(Auto Regressive Moving Average,ARMA)模型、回归分析法、卡尔曼滤波法等[10];而人工智能法则包括人工神经网络(Artificial Neural Network,ANN)、支持向量机(Support Vector Machine,SVM)、深度学习法等[11]。陈昌等[12]基于威布尔分布和最小二乘支持向量机对滚动轴承全寿命轴承实验数据进行了退化趋势预测,并取得了较准确的预测结果;李锋等[13]提出了一种基于双隐层量子线路循环单元神经网络(Double Hidden Layer Quantum Circuit Recurrent Unit Neural Network,DHL-QCRUNN),设计了双隐层结构以完成旋转机械状态的退化趋势预测,结果表明,该方法具有较高的预测精度和较高的计算效率。
滚动轴承的振动信号作为一种时序数据,当前采样点的数据与过去采样点的数据密切相关,同样也会影响未来的数据。循环神经网络(Recurrent Neural Network,RNN)由于其网络结构的特殊性,对于处理跟时间相关的数据与其他神经网络相比有明显的优势,而其变体长短期记忆(Long Short-Term Memory,LSTM)神经网络不仅拥有RNN时序数据预测良好的特性,而且解决了传统RNN梯度消失的问题[14]。由于其更为复杂的结构,因此具有更优秀的保留之前数据重要信息的功能,对于时序数据的预测有更好的能力。
主成分分析(Principal Component Analysis,PCA)是一种能够将高维数据进行降维的数据处理方法。通过从各个维度对数据进行分析,提取出数据中的重要信息,剔除冗余信息,降低数据计算量,提高计算速度。
本文提取了滚动轴承振动信号的时域特征指标、频域特征指标并依据时间相关性、单调性、退化阶段可分性对特征参数进行选择,剔除一些相关性不高的数据。采用PCA方法对筛选后的数据进行数据融合,提取出能够反映总体退化趋势的主成分,建立基于PCA-LSTM网络的轴承退化趋势预测模型,并对其进行精度验证。
1 方法原理
1.1 主成分分析(PCA)
在提取滚动轴承的特征参数时,若选择全部特征参数进行趋势预测,不仅会使计算复杂度大大增加,而且会导致数据的大量冗余。主成分分析[15]利用降维的思想对多个参数指标进行线性组合变换从而形成新变量,将原来的n维特征映射到k维上,且n>k,k维变量互不相关,且能反映原始数据足够多的信息。
如式(1)所示,将k个n维的新变量Z1,Z2,…,Zk用x1,x2,…,xm的线性组合来表示,令变换后的新变量的方差达到最小。
(1)
式中,αi=[αi1,αi2,…,αim]T(i=1,2,…,k)是协方差矩阵C中特征值λi的特征向量。协方差矩阵C为
(2)
通过主成分贡献率公式计算各个主成分的贡献率,由高到低依次选取特征值λ1,λ2,…,λm对应的主成分Zi,贡献率公式为
(3)
累计贡献率公式为
(4)
一般来说,累计贡献率达到85%~95%即可反映出绝大部分数据的信息[16],同时能有效降低原数据维度。
1.2 长短期记忆(LSTM)神经网络
LSTM不仅能从时间序列数据中提取数据之间的依赖关系,同时也解决了标准循环神经网络中不能连接到远处数据的问题。滚动轴承的振动信号数据是时序数据,当前时刻的振动信号与过去和未来之间的数据有着密切的联系。
LSTM神经网络由于其“门”结构的特殊性,能够连接到远处的数据,并保留过去数据的重要信息,其神经元结构如图1所示。

图1 LSTM神经元的具体结构
LSTM的工作原理如下。
① 上一时刻神经元的输出数据与当前时刻输入一并进入第一个交互层遗忘门中,经遗忘门处理后输出ft,其值为[0,1],与重要程度呈正相关性,此时遗忘门输出值表达式为
ft=σ[Wf·(ht-1,xt)+bf]
(5)
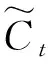
it=σ[Wi·(ht-1,xt)+bi]
(6)
(7)
(8)
③ 输出门通过上一时刻数据与当前输入生成原始输出ot,并通过tanh层将细胞状态Ct与ot相乘,得到最终的输出结果ht。计算公式为
ot=σ[Wo·(ht-1,xt)+bo]
(9)
ht=ot∘ tanh(Ct)
(10)
式中,W为各个门与细胞状态的权重矩阵;b为各个门和细胞状态的偏置项;σ为sigmoid激活函数;“·”为矩阵点积;“∘ ”为矩阵按元素相乘。
图2为本文的LSTM网络模型的拓扑结构,提取滚动轴承的时域特征参数和频域特征参数后使用PCA方法进行主成分的确定,隐含层设置为三层,分别是LSTM层、随机失活层(dropout)和回归层,最终输出预测的退化趋势。

图2 LSTM网络在滚动轴承退化趋势预测的拓扑结构
1.2.1 数据标准化
由于在实际输入数据时可能出现量纲不同、范围不同的情况,对于神经网络来说需要平等地处理每个参数的影响。所以对最终输入的数据会进行标准化处理。标准化的计算公式为
(11)
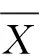
(12)
1.2.2 LSTM的模型参数选择
在实际对模型进行训练时,需要确定LSTM的一系列超参数,本文的LSTM预测模型的超参数设置如表1所示。
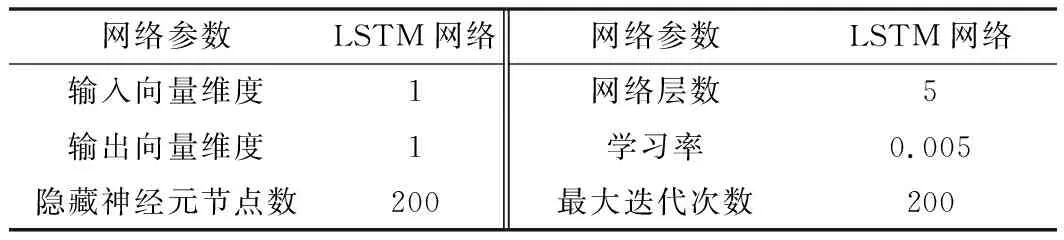
表1 LSTM网络训练参数
为了防止发生过拟合的现象,在LSTM隐含层中添加了一层随机失活层,可以有效避免其在测试集中表现出的过拟合现象,随机失活概率设置为0.2。在求解器方面选择了Adam自适应矩估计求解器,初始学习率设置为0.005,并在每经过一半的训练之后乘以0.2以降低学习率,梯度阈值设置为1以防止梯度爆炸,激活函数则为tanh。
1.2.3 模型评价指标
通过预测值和真实值的对比可以看出LSTM在退化趋势预测中的表现,为了量化其预测效果,选取RMSE(Root Mean Square Error,均方根误差)和MAPE(Mean Absolute Percentage Error,平均百分比误差)以对算法的预测性能进行衡量,RMSE和MAPE的计算公式为
(13)
(14)
式中,ypi为在i时刻的预测值;yti为在i时刻的真实值。
2 数据算例
2.1 数据选择
本文采用的滚动轴承退化趋势数据是由西安交通大学雷亚国教授团队提供的[17]。该数据集记录了滚动轴承从正常状态到由于故障失效状态的完整的全寿命周期数据,滚动轴承的数据试验台如图3所示。
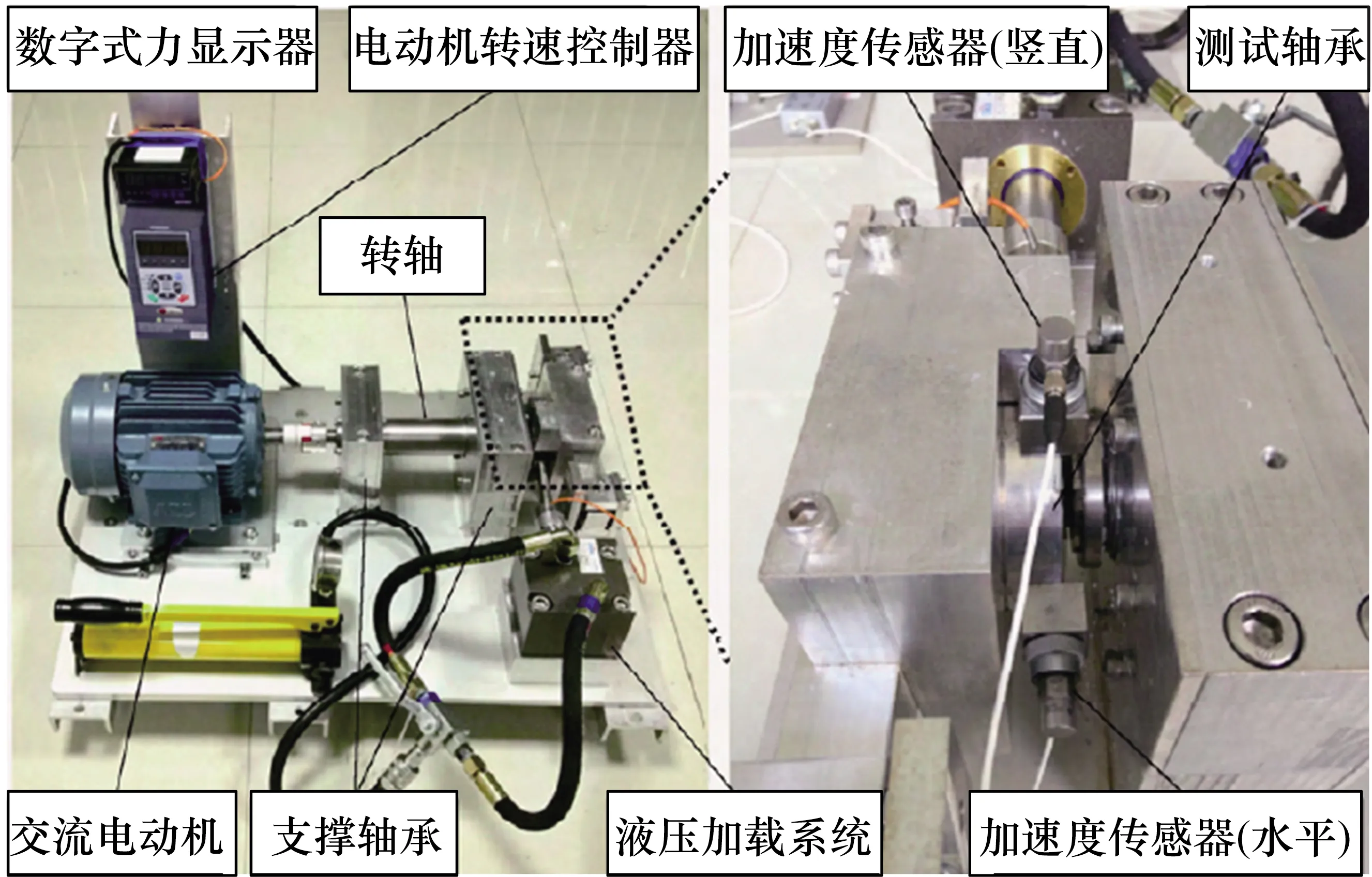
图3 滚动轴承全寿命试验台
试验轴承为LDK UER204滚动轴承,在进行试验时,分别将两个PCB 253C33单向加速度传感器安装在竖直方向和水平方向上,振动信号通过DT9837便携式动态信号采集器采集,采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。具体采样设置情况如图4所示。
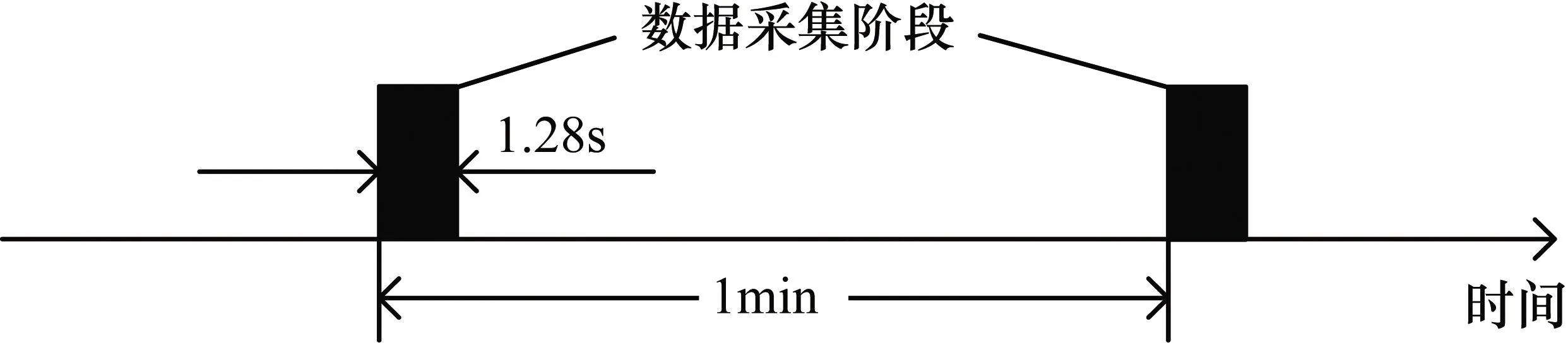
图4 振动信号的采样设置
试验总共有3种工况,每一类工况下选取额定寿命相同的5个轴承进行试验,以工况一为例,5个轴承在失效时的失效位置并不相同,分别包括内圈故障、外圈故障和保持架故障,具体失效位置如图5所示。
在对轴承进行退化趋势预测时,需要根据轴承振动量的大小来确定轴承是否具有典型的全寿命退化特征,根据选择比较之后确定了数据集中的轴承1_1具有典型的轴承退化趋势,其趋势具有明显的时间相关性、单调性和退化可分性[18]。轴承1_1的振动信号如图6所示。

图5 轴承各失效位置示意图
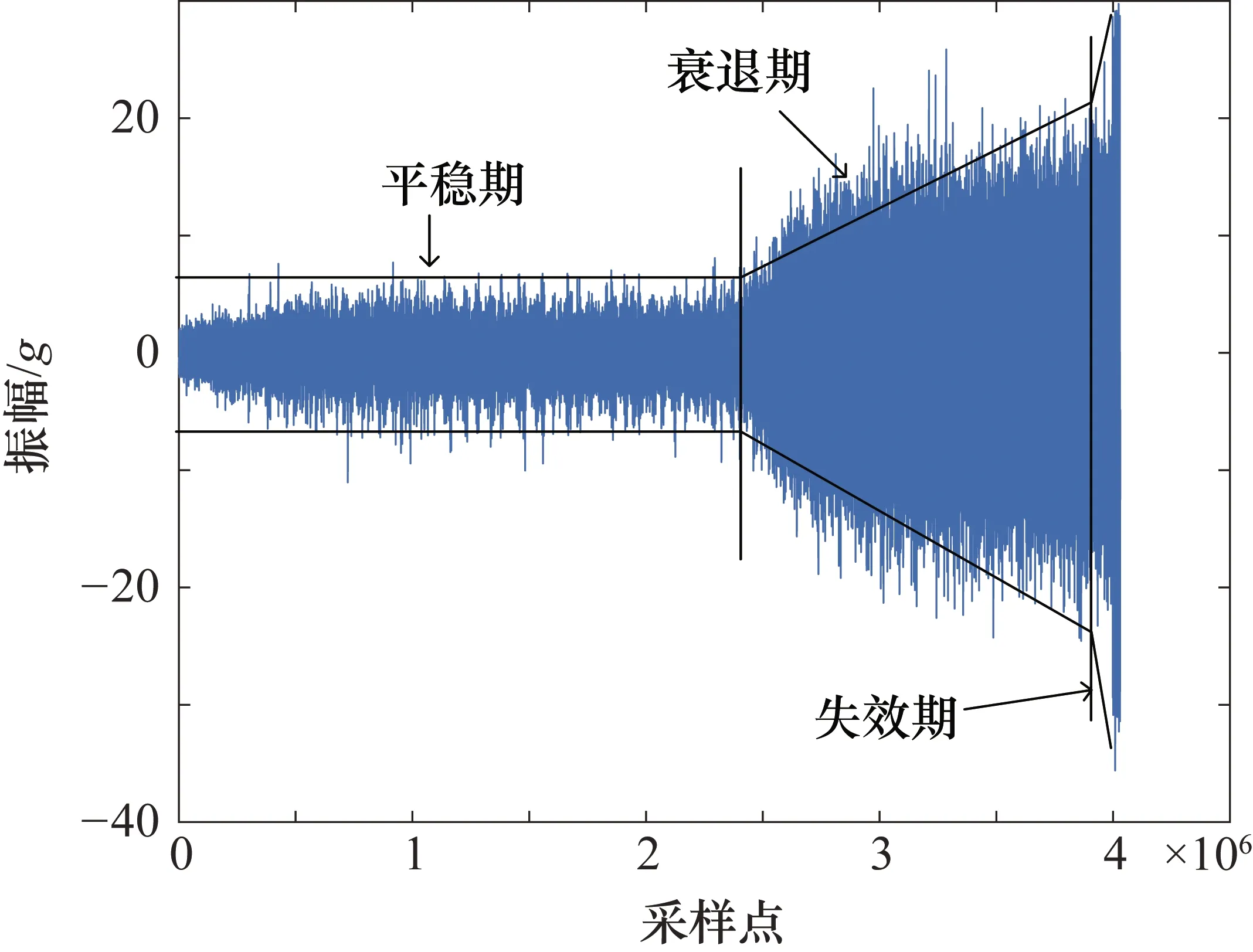
图6 轴承1_1的振动信号
对振动信号提取其时域特征参数和频域特征参数后进行筛选,删除其中表现效果较差和与时间序列相关性不大的特征指标,最终得到了5个指标:时域均方根值、频域方差、时域方差、时域绝对值的平均值和频域平均幅值,具体如图7所示。
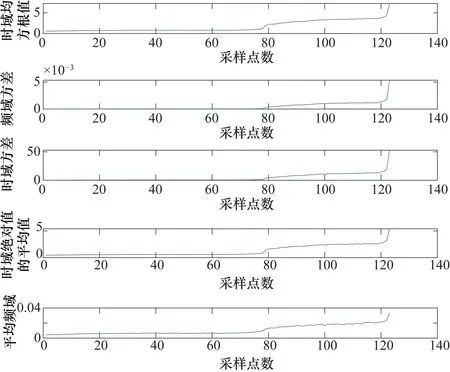
图7 轴承1_1退化特征参数集
对上述5个特征指标进行PCA的数据融合后,主成分的累计贡献率如表2所示。
由表2可知,第一个主成分Z1贡献率为96.531%,而累计贡献率一般设置在85%~95%,说明第一个主成分Z1与原始数据高度相关,基本可以反映其全部信息,所以只选取第一个主成分作为神经网络的预测对象,具体图像和其他参数指标对比如图8所示。
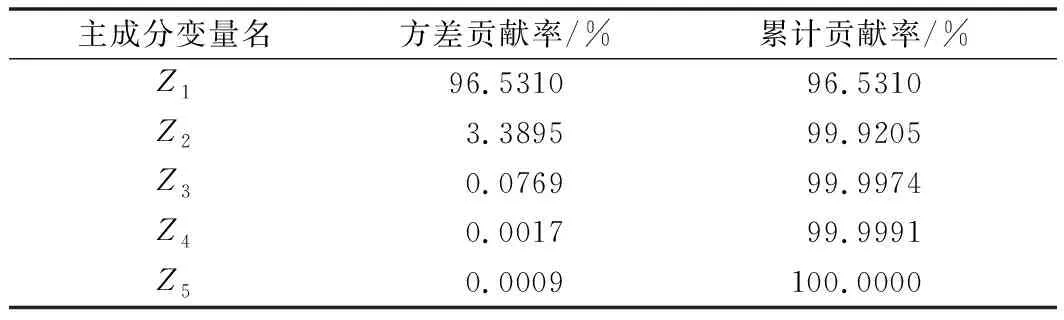
表2 主成分贡献率及累计贡献率
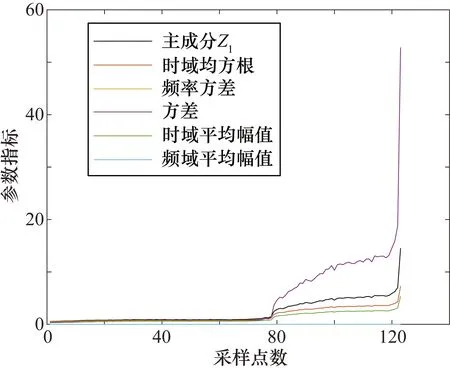
图8 主成分分析和其他指标参数对比
由图8可看出,主成分Z1具有比除方差外的其他指标更好的特征区分性,且相比于方差有更好的平滑性,说明PCA能够在特征可分性和单调性上取得较为均衡的效果。
2.2 数据训练与预测
对主成分分析Z1的数据进行训练集和测试集的划分,将第一个点作为训练集的起始点,用全寿命的退化趋势数据进行退化趋势预测。在数据划分过程中,若训练集过少,会导致网络训练不准确,若训练集过多,则可能发生过拟合现象。多次实验后确定使用前85%的数据作为训练集,后15%的数据作为测试集验证网络的预测准确度。并且在隐含层之后加了一层随机失活层防止其过拟合现象的发生。在预测过程中,每次预测下一个点时,使用真实值来更新网络,防止累计误差的产生。为了显示LSTM网络预测的良好性,选用Matlab中的非线性自回归(Nonline Auto Regressive,NAR)神经网络与其进行对比[19]。NAR模型也是一种对时间序列进行分析的动态神经网络模型,由于NAR神经网络的输出信息也会作为输入信息进行反馈,所以也十分适合对时间序列数据进行预测。经反复调整后确定NAR神经网络为3层网络,分别是输入层、隐含层和输出层,其隐含层节点数为10个,延迟阶数为10。预测结果如图9所示。
由图9可看出,基于PCA-LSTM的神经网络的退
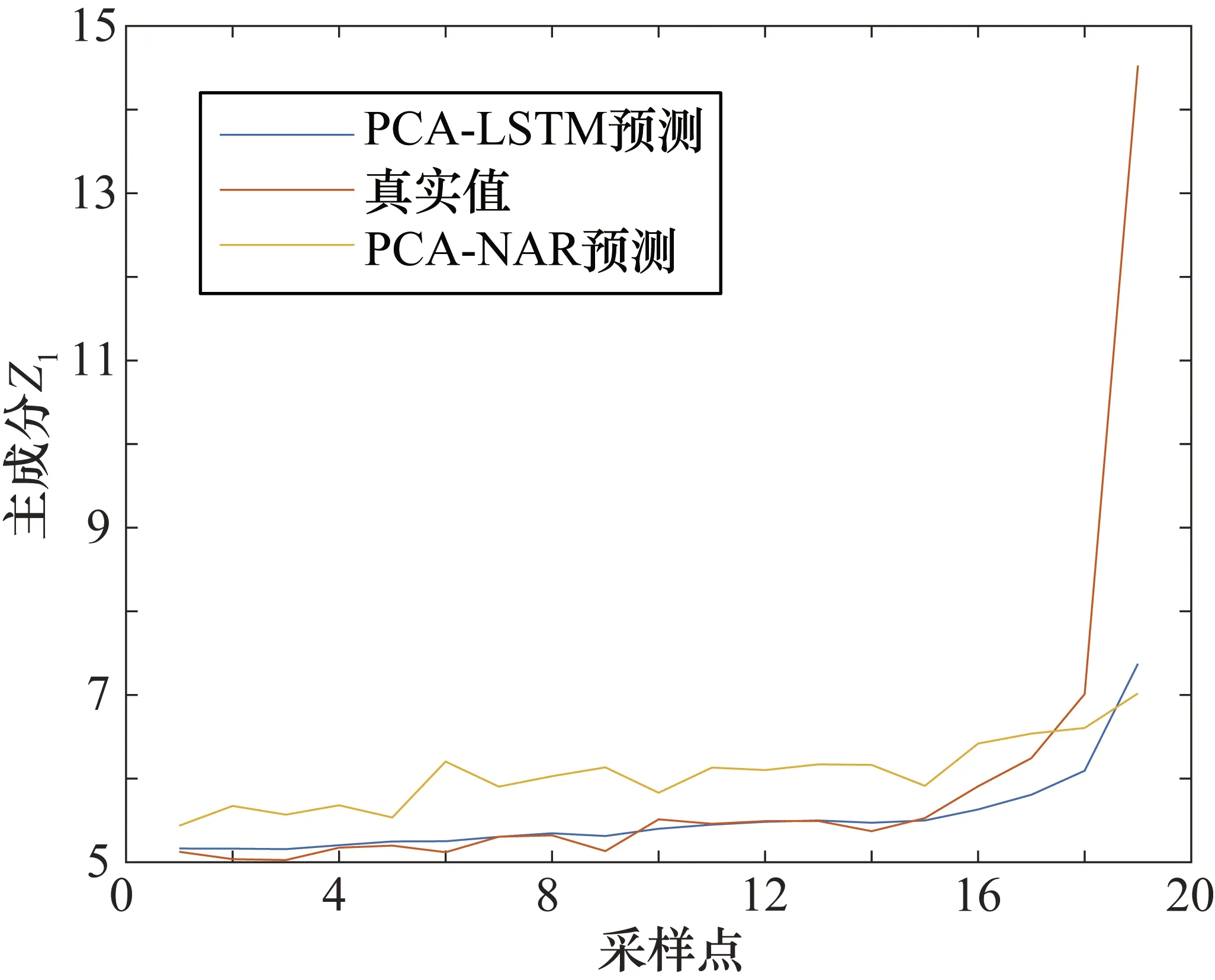
图9 不同神经网络预测对比
化趋势预测模型明显优于基于PCA-NAR的神经网络,说明了LSTM对时序数据有良好的预测能力,为了量化其预测效果,将不同神经网络的RMSE和MAPE分别列出,如表3所示。

表3 不同神经网络的评价指标对比
由图9和表3可知,基于PCA-LSTM的滚动轴承退化趋势预测模型在RMSE和MAPE上均优于NAR神经网络,RMSE减少了0.1638,MAPE降低了8.0163%。上述数据充分说明了LSTM网络在滚动轴承退化趋势预测上的优越性,能够有效预测之后的退化趋势。
3 结束语
本文使用了主成分分析对滚动轴承的特征指标进行了数据融合,并使用LSTM神经网络对主成分分析之后的指标进行了趋势预测,取得了较好的预测结果,相比于其他神经网络更为精确,为轴承的退化趋势预测提供了一种新的思路。
① 主成分分析有效地反映了滚动轴承在退化过程中的不同阶段,相对于方差等指标有更好的平滑性,在单调性和趋势可分性上取得了较为平衡的效果,并且降低了数据的输入维度,减小了高维数据的计算量。
② 通过LSTM神经网络对融合后的主成分进行趋势预测,加入了随机失活层,防止因网络参数和训练集的原因导致过拟合现象的发生,加强了其泛化性。
③ 预测结果表明基于PCA-LSTM的滚动轴承退化趋势预测模型能够有效预测轴承退化趋势,且误差相比于其他神经网络(NAR网络)明显较低,显示出其在滚动轴承退化趋势预测上的有效性和优越性。
