GA-BP算法预测滚动轴承退化趋势

杨 乐， 王景霖， 李胜男， 邵辰彤， 封锦琦

(1.故障诊断与健康管理技术航空科技重点实验室，上海 201601；2.航空工业上海航空测控技术研究所，上海 201601； 3.航空工业北京长城航空测控技术研究所，北京 101111)

滚动轴承是机械装备中保持运动精度和提高机械效率的重要零部件之一，在实际工程应用中，滚动轴承的工作环境相对比较恶劣，由于装备长时间、高强度运转，加之安装使用不当、维护不及时和润滑不良以及自身缺陷，使得滚动轴承成为机械设备中最容易损坏的零件之一[1-3]。这就对装备零部件的可靠性、维修性、保障性、安全性和测试性提出了更高的要求。因此，对滚动轴承进行退化趋势分析和剩余寿命预测既能避免处于工作状态的装备突然失效造成事故，又可以为设备后期维修提供决策支持。由此可见，故障预测在装备健康使用中起着重要作用。国内外学者已经对故障预测进行了大量的攻关研究。

目前，学术界与工程应用中关于故障预测研究与应用已经取得了一些成果，主要有基于模型的故障预测方法和基于数据的故障预测方法，其中基于数据的故障预测方法获得了广泛关注[4-5]。基于数据的故障预测方法的一般思路是根据被预测对象的历史数据，对历史数据进行分析；采取合适的特征提取方法对原始数据进行处理，目的是得到能表征被预测对象剩余寿命的性能指标；利用合适的预测算法，建立关于性能指标的故障预测模型，通过调节参数，对性能指标进行预测；通过结果分析，得到设备退化趋势分析结果，从而实现对设备的故障预测。常用的基于数据的故障预测方法主要是利用神经网络和支持向量机进行故障预测[6]。Widodo等[7]提出了生存分析与支持向量机相结合的寿命预测模型，使用相关分析法确定轴承特征指标，作为输入参数预测滚动轴承剩余寿命；邱晓梅[6]利用粒子群算法优化BP神经网络参数，进行基于轴承退化状态的剩余寿命预测；曾庆凯[8]利用经验模态分解结合Kriging方法的预测模型，并将轴承剩余寿命表示为剩余寿命百分比进行寿命预测；Ren等[9]在提取轴承振动信号时域、频域信号的基础上，提出一种基于深度神经网络模型的算法进行寿命预测；燕晨耀[10]在提取滚动轴承振动信号时域、频域特征指标基础上，分别利用局部均值分解理论对原始信号降噪和主成分分析法对特征信号降维处理，同时采用支持向量机和相关向量机理论进行滚动轴承寿命预测。本文在BP神经网络的基础上，利用遗传算法(Genetic Algorithm，GA)对BP神经网络的各项参数进行寻优计算，并将轴承时域指标融合为特征矩阵作为输入参数，将频域特征指标作为输出参数，在对轴承退化状态划分的基础上进行轴承衰退期的退化趋势预测，根据神经网络原理建立时域输入特征集与频域输出指标之间的相关关系，通过预测频域指标的变化趋势反映出轴承的退化趋势。

1 理论基础

1.1 BP神经网络理论

BP神经网络是一种多层前馈神经网络，BP神经网络的优点是信号前向传递，误差反向传递[11]。BP神经网络的数据处理过程为：信号首先经过输入层进入神经网络，然后通过隐含层进行迭代计算，最后通过输出层输出。当神经网络具有多个隐含层时，每一层的神经元状态只受上一层神经元影响，如果输出层得不到预期结果，则误差进行反向传播，BP神经网络根据预测误差不断调整网络权值和阈值，直到BP神经网络的输出值逼近预期值。BP神经网络的三层拓扑结构如图1所示。

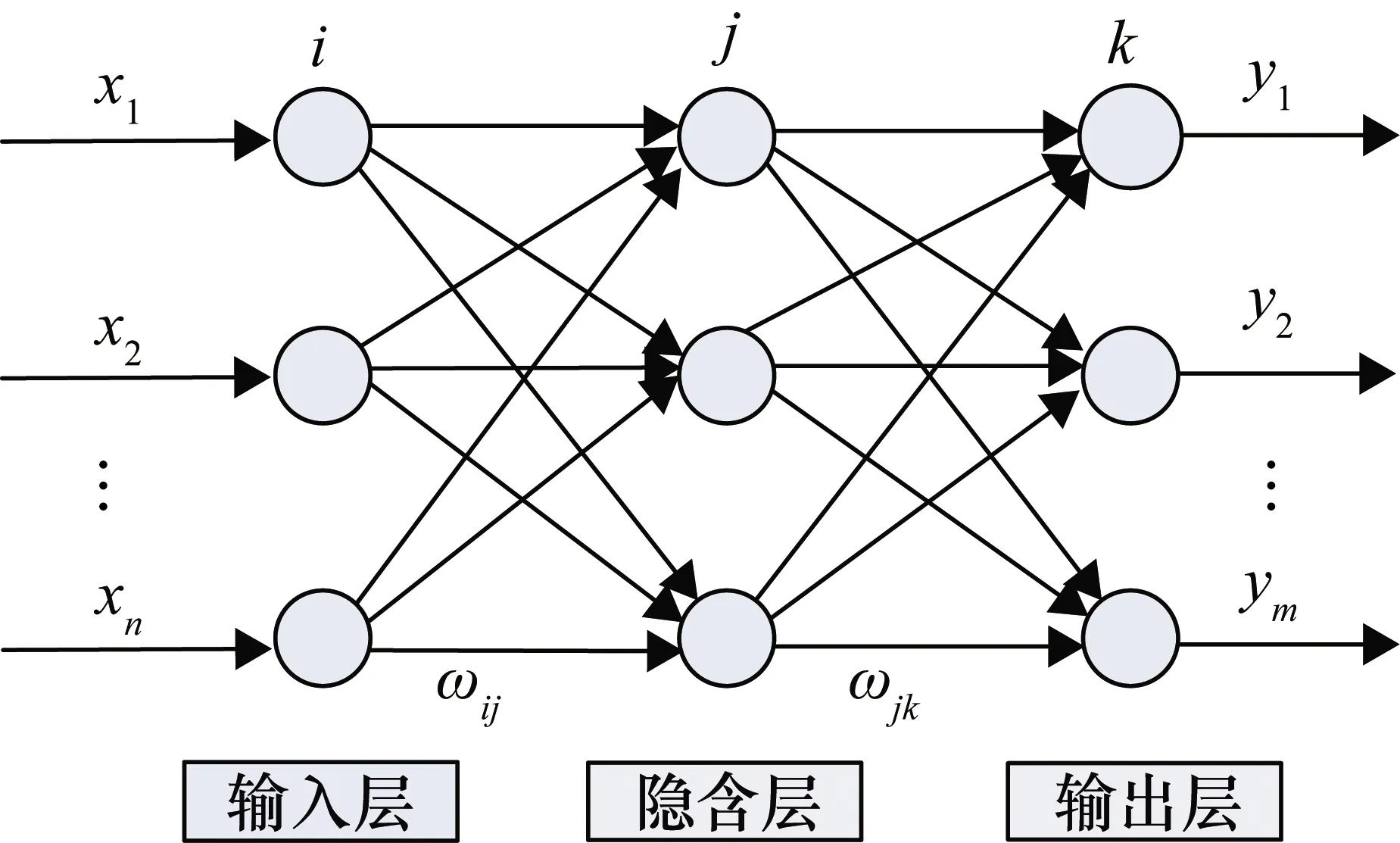
图1 BP神经网络网络拓扑图

图1中，x1,x2,…,xn为BP神经网络的输入参数;y1,y2,…,ym为BP神经网络的输出值;i,j,k分别为输出层、隐含层、输出层的神经元数量；ωij为输入层到隐含层的神经元网络权值；ωjk为隐含层到输出层的神经元网络权值。

BP神经网络进行预测时，首先要对网络进行训练，使网络具有记忆和预测能力，训练过程包括以下7个步骤。

① 初始化网络：根据输入层参数x和输出层参数y的个数确定输入层节点数n、输出层节点数m和隐含层节点数l，初始化网络权值ωij、ωjk,设置隐含层阈值a的初始值、输出层阈值b的初值，初始化其他参数。

② 隐含层输出计算：隐含层输出值H的计算公式为

(1)

式中，f为隐含层神经元激励函数，该函数的表达式为

(2)

③ 输出层输出计算：输出层的输出值计算与隐含层的输出Hi有关，计算公式为

(3)

④ 误差计算：根据输出层的输出Ok和预期输出Yk来计算预测误差ek，计算公式为

ek=Yk-Ok，k=1,2，…,m

(4)

⑤ 更新权值：根据误差ek更新网络权值ωij、ωjk，计算公式为

(5)

ωjk=ωjk+ηHjek,j=1,2,…,l,k=1,2,…,m

(6)

式中，η为学习速率。

⑥ 阈值更新：根据误差e更新隐含层阈值a、输出层阈值b，计算公式为

(7)

⑦ 判断算法是否结束：当误差e达到精度要求或者迭代次数达到最大时，算法结束，否则，返回步骤②继续进行预测。

1.2 GA理论

GA是依据自然界遗传机制和生物进化理论形成的一种随机寻优方法。GA的基本操作如下。

① 选择操作：是指从旧群体中以一定的概率选择个体到新群体中，个体被选中的概率由个体适应度决定，个体适应度越好，被选中的概率就越大。

② 交叉操作：是指从个体中随机选择两个个体，随机选取一点或多点染色体进行位置交换，产生新的优秀个体，交叉操作如图2所示。

图2 交叉操作

③ 变异操作：是指从群体中随机选取一个个体，选择染色体中的一个点进行变异以获取更优秀的个体，变异操作如图3所示。

图3 变异操作

GA的基本要素包括：染色体编码方法、适应度函数、遗传操作和运行参数。染色体编码方法主要有二进制编码、实数编码等；适应度函数是指根据进化目标编写的计算个体适应度值的函数，每个个体的适应度值由适应度函数求得并提供给选择算子进行选择；遗传操作包括指选操作、交叉操作和变异操作。

GA优化的思路是通过优化BP神经网络的初始权值和阈值，使优化后的神经网络能够更好地预测函数输出，优化的要素包括：种群初始化、适应度函数，以及选择、交叉、变异操作。GA网络实现的步骤分为以下几个部分。

(1) 种群初始化。

每个个体均为一个实数串，每个个体包含了连接了输入层与输出层的权值、连接隐含层与输出层的权值、输出层阈值和隐含层阈值共4个部分。因此，在网络已知的情况下，就可以构成一个结构、权值、阈值确定的神经网络。

(2) 选择适应度函数。

由个体得到的BP神经网络的初始值和阈值，用训练数据训练网络后预测系统输出，个体适应度值F由预测输出值与期望输出值之间的误差绝对值计算得到，计算公式为

(8)

式中，n为网络输出节点数；yi为网络中第i个节点的期望输出值；oi为网络中第i个节点预测输出值；k为系数。

(3) 执行选择操作。

GA常用的选择操作有轮盘赌法、锦标赛法等，本文选用轮盘赌法。轮盘赌法的原理是基于适应度比例的选择策略，每个个体i的选择概率pi的计算公式为

(9)

式中，Fi为个体适应度值；k为系数；N为种群个体数目。

(4) 执行交叉操作。

GA中，由于个体采用实数编码，所以交叉操作方法采用实数交叉法，第k个染色体ak和第l个染色体al在j位的交叉操作公式为

(10)

式中，b为区间[0,1]内的随机数。

(5) 执行变异操作。

在执行变异操作时是选择第i个个体的第j个基因aij进行变异，变异操作的公式为

(11)

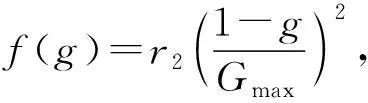
2 方法步骤

本文对滚动轴承的寿命预测主要通过以下步骤实现。

① 特征参数提取：首先从轴承全寿命周期振动数据中提取时域、频域特征参数，然后计算特征参数与轴承剩余寿命的相关系数，确定阈值以选取合适的特征指标构成预测参数集。

② 轴承退化阶段划分：根据轴承全寿命周期的振动信号特性，划分轴承的退化状态。

③ 定义网络训练标签：以轴承退化起始时刻为预测起点，预测轴承从退化开始时刻至完全失效时间段内的退化趋势。

④ BP神经网络训练：确定网络训练参数，以轴承时域特征指标组成的特征参数集为输入，以频域特征向量为输出，建立输入集于输出标签之间的关系模型，对网络进行训练。

⑤ 退化趋势预测：利用训练好的模型对轴承退化趋势进行预测，进而达到预测剩余寿命的目的，验证模型准确性，并将GA优化后的神经网络与初始BP网络进行比较，分析其结果。

3 滚动轴承特征参数集构造

3.1 滚动轴承试验台及试验数据介绍

本文采用的滚动轴承全寿命周期数据由西安交通大学雷亚国团队提供(XJTU-SY轴承数据集)，试验台如图4所示[12]。试验台采取了两个PCB352C33单向加速度传感器分别通过磁座固定于测试轴承的水平与竖直方向上。试验中使用DT9837便携式动态信号采集器采集振动信号。采样参数设置如图5所示，试验中设置的采样频率为25.6 kHz，采样间隔为1 min，每次采样时长为1.28 s。

XJTU-SY轴承数据集分别做了3种工况下5个轴承的加速退化试验，表1给出了测试轴承的详细信息，包括其对应的工况、数据样本总数、基本额定寿命L10、实际寿命和失效位置。如表1所示，以工况轴承1-1为例，工况1的转速为2100 r/min，径向力为12 kN，每隔1 min采集一次数据，每次采集数据的时间为1.25 s，采集的数据放在CSV文件中，轴承1-1的全寿命周期一共采集123次，样本总数为123个CSV文件，每个CSV文件中有32768行、2列数据，第1列为水平方向信号，第2列为垂直方向信号，L10为轴承的基本额定寿命，在加速度实验中，轴承1-1实际寿命为2 h 3 min，故障类型为外圈故障。本文选择轴承1-1水平方向振动信号进行故障数据训练与预测。

图4 轴承加速寿命试验台

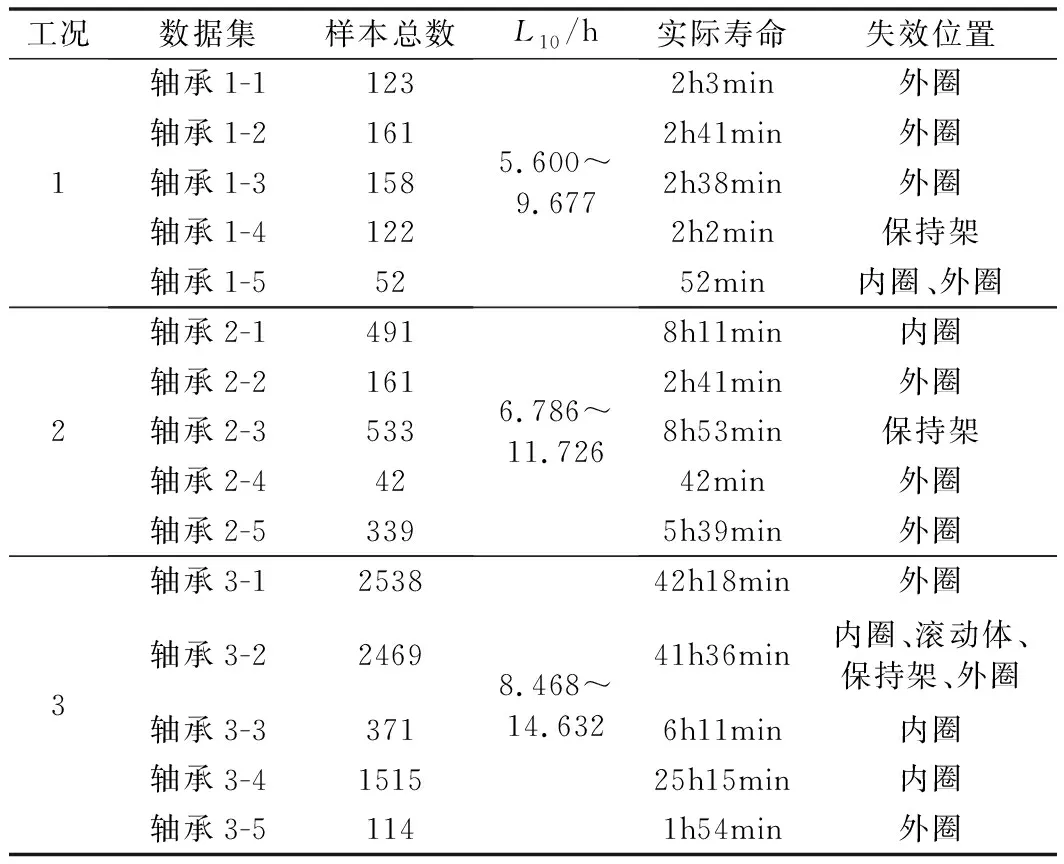
表1 XJTU-SY轴承数据集

3.2 特征参数提取及特征集构造

3.2.1 振动数据降噪处理

在试验采集到的轴承原始振动信号中含有较多的噪声，噪声信号会覆盖振动信号本身所携带的状态信息，导致信号波形发生变化甚至淹没故障特征频率。因此，原始信号绘制的曲线会产生不规则的凸起，为了减弱噪声对信号的干扰，需要采取一定的降噪方法对原始信号进行处理。本文采用五点滑移平均法进行降噪，计算公式为

(12)

式中,i=3,4,…,m-2。

以轴承1-1的均方根为例，用五点滑移平均法[13]降噪前后的对比图如图6所示,可以看出，降噪后的特征指标去除了数据的毛刺，曲线比原始信号的曲线更加光滑。

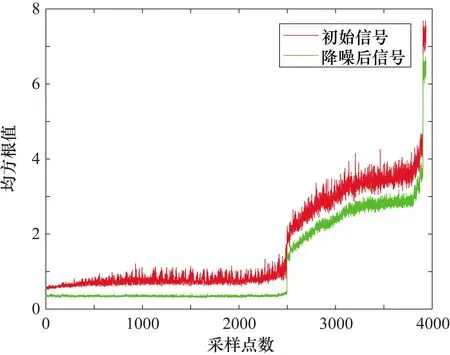
图6 降噪前后均方根值对比

3.2.2 特征数据集构造

在振动信号的时域、频域的众多信号中，如何选取合适的特征值来表示轴承的退化趋势是轴承退化趋势预测前期需要解决的问题，本文采用的方法是：首先计算轴承的剩余寿命百分比，计算当前采样点时刻轴承剩余寿命与全寿命周期的比值得出剩余寿命百分比，将剩余寿命百分比限定在[0,1]之间。然后计算时域、频域特征指标与剩余寿命百分比之间的相关系数[14]。相关系数是表征两个变量之间线性相关程度的量，若有两个向量x=[x1,x2,…,xn],y=[y1,y2,…,yn]，则x、y之间的相关系数计算公式为

(13)

本文提取的时域指标有均方根、峰峰值、方差、峭度、偏度、波形因子、脉冲指标、裕度和方根幅值，频域指标有平均频率、中心频率和频率标准差。由于特征指标差别较大，计算相关系数时会造成较大误差，因此，需要将特征指标归一化到[-1,1]，计算公式为

(14)

式中，x为特征指标；xnor为归一化后的结果；ymax=1；ymin=-1；xmax为特征指标序列中的最大值；xmin为特征指标序列中的最小值。利用式(14)计算轴承1-1水平方向振动信号特征指标归一化后与剩余寿命百分比，结果见表2。

根据表2计算出的相关系数，应选出符合轴承退化趋势的特征指标，即选择与剩余寿命相关性强的特征指标作为输入输出矩阵。本文采用设定阈值的方法来确定选取的特征指标，相关系数绝对值大于阈值时，将对应的特征指标构造成输入输出矩阵，阈值取各相关系数绝对值的平均值,计算得到阈值为0.6444，经过筛选后，选取相关系数绝对值大于阈值的特征指标。本文选取6个时域指标作为输入矩阵，一个频域指标作为输出矩阵，通过神经网络模型，建立两者之间的函数关系，预测频域指标的变化趋势来反映轴承的退化趋，构建的特征指标集如表3所示。均方根值、峰峰值、方差、峭度、波形因子、方根幅值为输入矩阵，平均频率为输出矩阵。

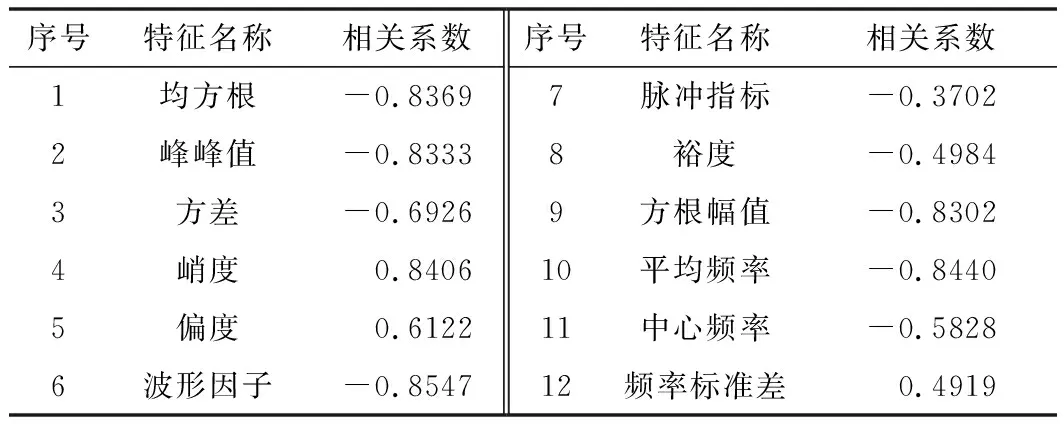
表2 特征指标与剩余寿命百分比之间的相关系数

表3 特征指标集

4 退化趋势预测

4.1 轴承退化状态划分

图7为轴承1-1的全寿命周期振幅图，由图7可以看出，轴承先是经过一定时间的稳定运行阶段，此时振幅维持在-2～2之间，到达第2.5×106个采样点时，振幅突然增大，随后逐渐上升，此阶段，振幅在-15～15之间，最后在第3.9×106个采样点时，振幅又一次上升，此时振幅超过20，因此轴承运行阶段可分为3个阶段：稳定运行期、衰退期和失效期。

稳定运行期中，加速度幅值变化较小，长时间保持在稳定状态，相应的特征指标变化也不明显，此时期内轴承没有明显的退化趋势，因此该时期内对轴承做退化趋势预测没有实际意义。在衰退期，轴承加速度幅值逐渐增大，变化趋势明显但不迅速，相应的特征指标变化趋势也逐渐增大。在失效期，轴承加速度幅值激增，且在短时间内振幅增加明显。由于轴承衰退期和失效期的数据量差别明显，失效期的数据样本较之衰退期的样本量极少，为选择有代表性的数据进行趋势预测，本文选择轴承衰退期的振动信号进行轴承退化趋势预测。

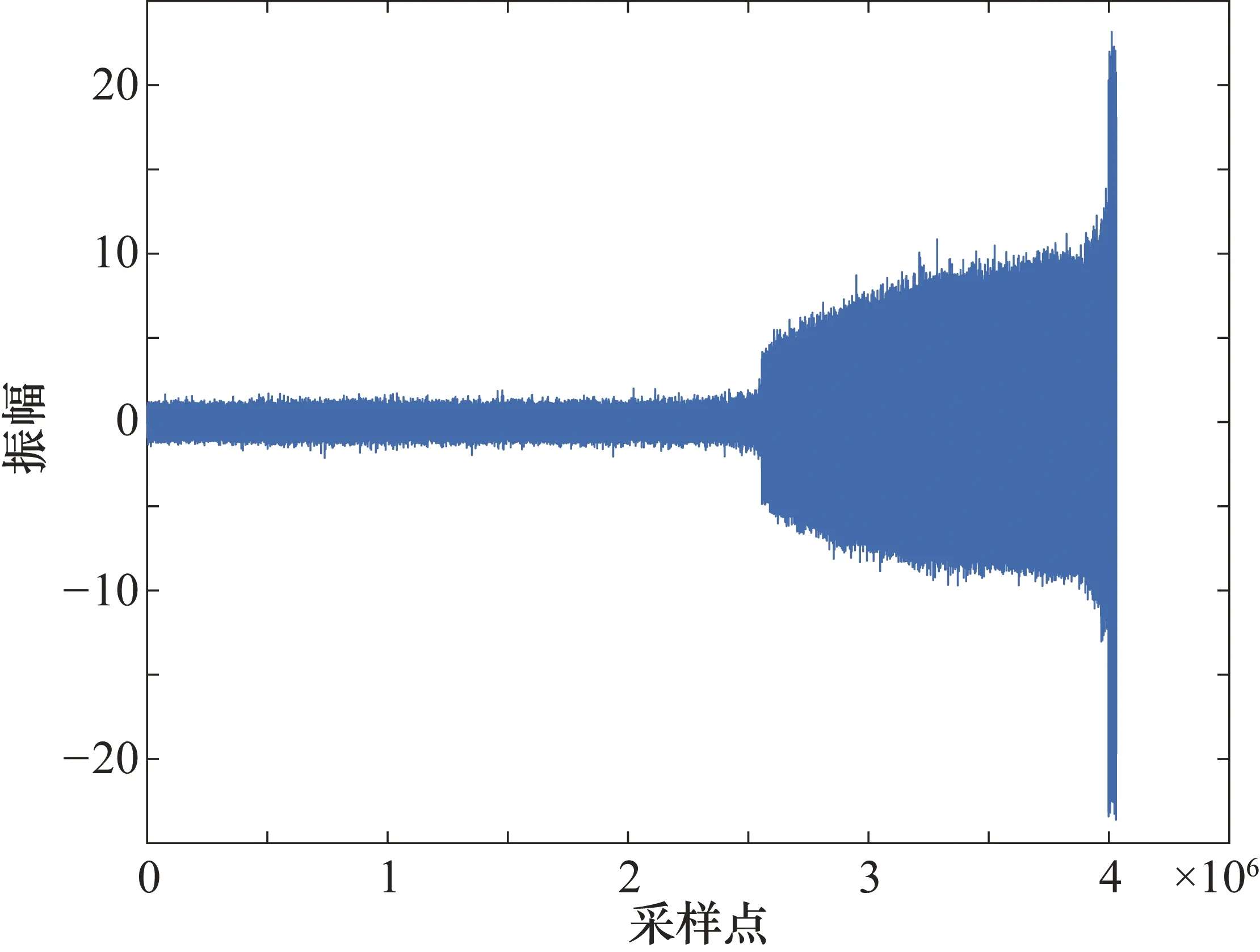
图7 轴承1-1全寿命周期振幅图

4.2 BP神经网络预测

用BP神经网络进行预测时，可以分为3个步骤：BP网络搭建、BP网络训练和BP网络预测。搭建BP神经网络时，由于本文设置的输入为6个参数，输出为1个参数，所以构建的BP神经网络输入层节点数为6，输出层节点数为1，分别设置隐含层为单隐含层和多隐含层。BP神经网络的训练用输入输出参数进行网络训练，使训练好的网络能够实现预测功能。选择输入输出数据的90%作为训练数据集，10%作为测试集用于测试网络的预测功能。图8为单隐含层BP神经网络的预测结果，图9为双隐含层的预测结果,可以看出预测结果与期望输出间误差较小，经计算可知单隐含层BP网络的预测结果与期望输出间的均方误差为0.0081,双隐含层BP网络的预测结果与期望输出间的均方误差为0.0058。

4.3 GA-BP网络预测

GA优化BP神经网络预测模型分为3个步骤：确定BP网络结构、GA优化参数和网络预测。网络结构由拟合函数的输入输出参数个数来确定，同时，GA个体长度也由拟合函数的输入输出参数个数确定。因为种群中的每个个体都包含了一个网络中所有的权值和阈值，因此使用GA优化BP神经网络的权值和阈值时，个体通过适应度函数计算个体适应度值，GA通过选择、交叉、变异操作找到最优个体。当种群中最优个体被找到后，用最优个体对网络的初始阈值和权值赋值，训练网络用于预测。

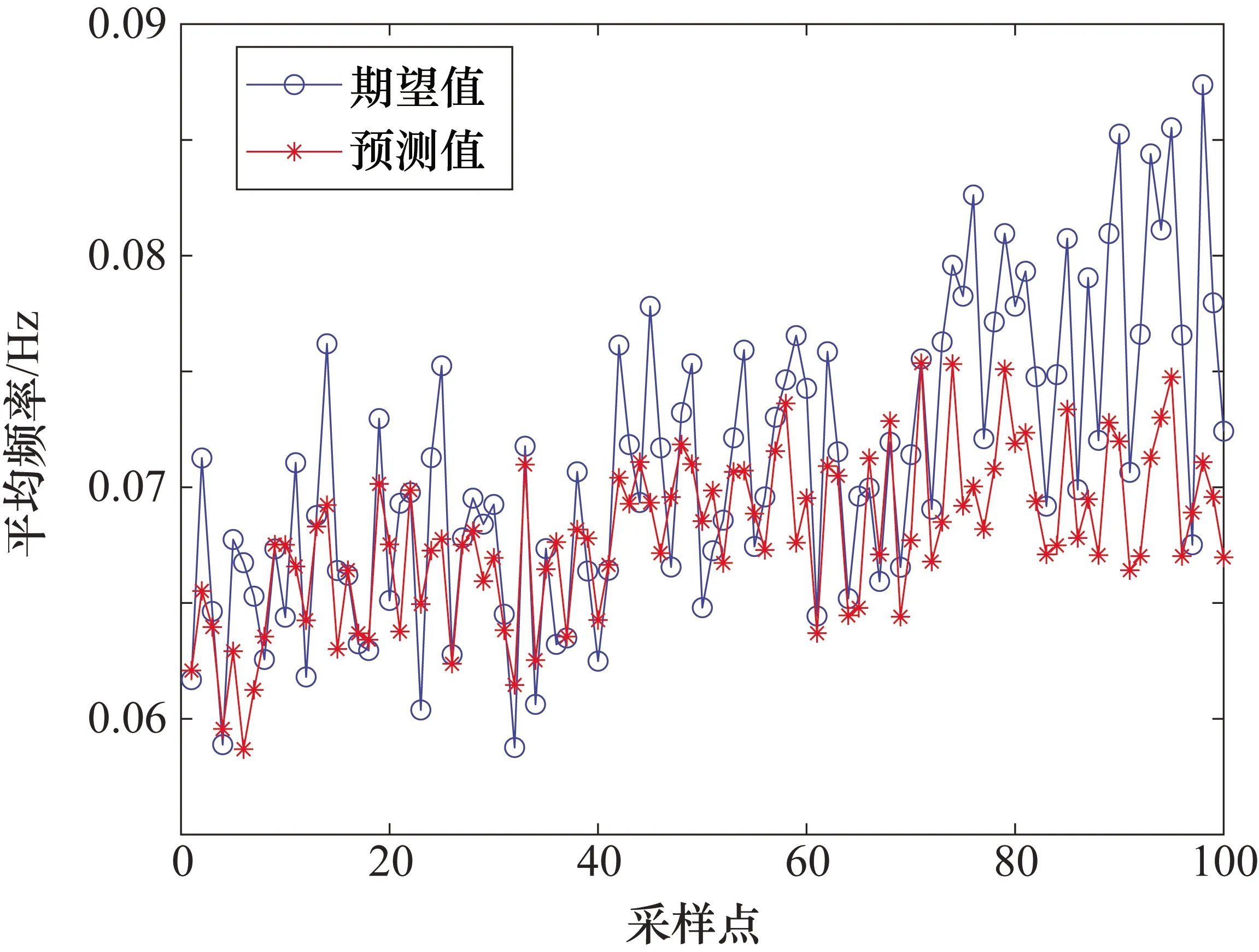
图8 单隐含层BP神经网络预测结果

本文中，由于输入输出参数分别为6和1,所以设置BP神经网络输入层节点数为6,输出层节点数为1，设置隐含层节点数为5，因此共有权值个数为35个，共有阈值个数为6个，GA个体编码长度为41。同样选择输入输出数据的90%作为训练数据集，10%作为测试集用于测试网络的预测功能。图10为GA优化BP神经网络后的预测结果，由图10可知，其优于期望结果，经计算可得预测结果与期望输出间的均方误差为0.0041。

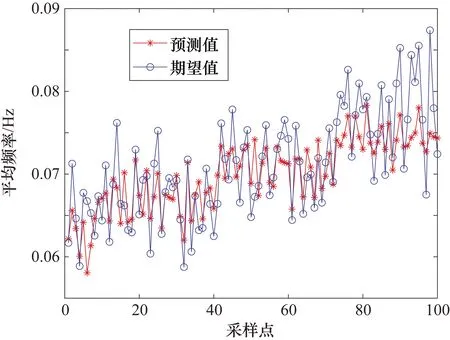
图10 GA-BP算法预测结果

5 结束语

本文分别使用单、双隐含层BP神经网络和GA-BP神经网络进行轴承退化趋势预测，并与使用粒子群优化后的BP神经网络预测结果进行对比，图11为4个网络预测结果与期望输出之间的误差的对比图。从图11中可以看出，本文所提出的基于GA优化BP神经网络的参数算法预测误差最小。表4列出了4种方法的预测误差的均方根误差值、平均值误差，可以看出经过GA优化后的算法误差在4种模型中的预测误差最小，GA优化后的预测误差的均方根值为0.0041，平均误差为0.0033。

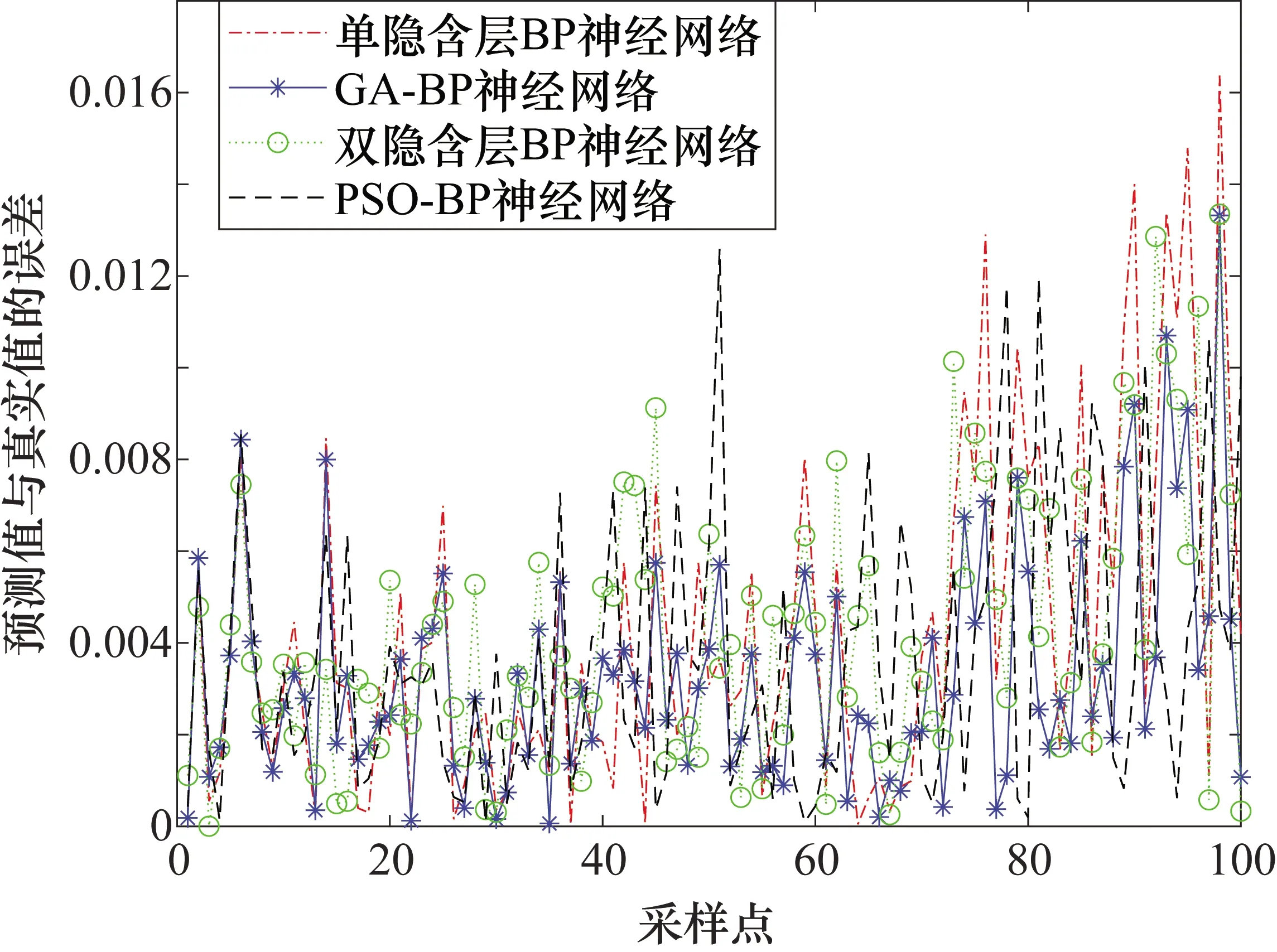
图11 预测结果误差对比

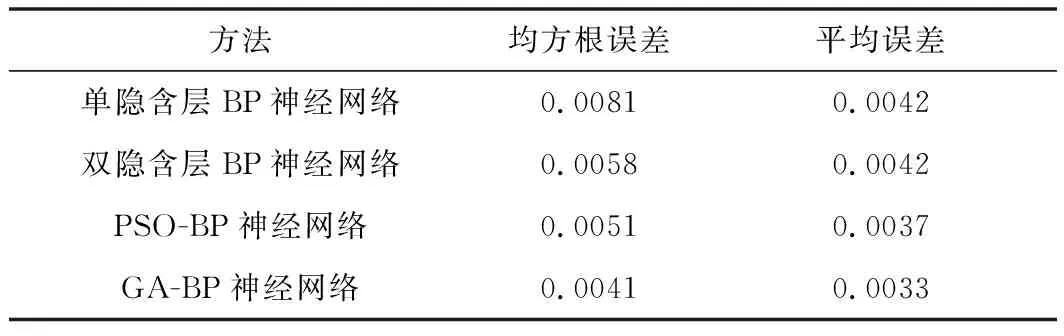
表4 预测误差对比