有关“连续体碰撞”的模型进阶与试题分析
2021-12-09李旭斌陈晓陆
李旭斌 陈晓陆
(中国人民大学附属中学朝阳学校,北京 100028)
高中物理学习认知发展规律满足从感性到理性、从具体到抽象、从简单到复杂的认知进阶规律.米粒流撞击台秤产生示数的现象在生活中易于观察,学生易于联想,以该感性、具体的连续体碰撞模型为抓手,逐渐延伸至较为抽象的电子流碰撞模型、理想气体分子碰撞模型、光子碰撞模型这些对象模型,并且从较为简单的完全非弹性碰撞延伸至较为复杂的完全弹性碰撞、非完全弹性碰撞这些过程模型(表1).
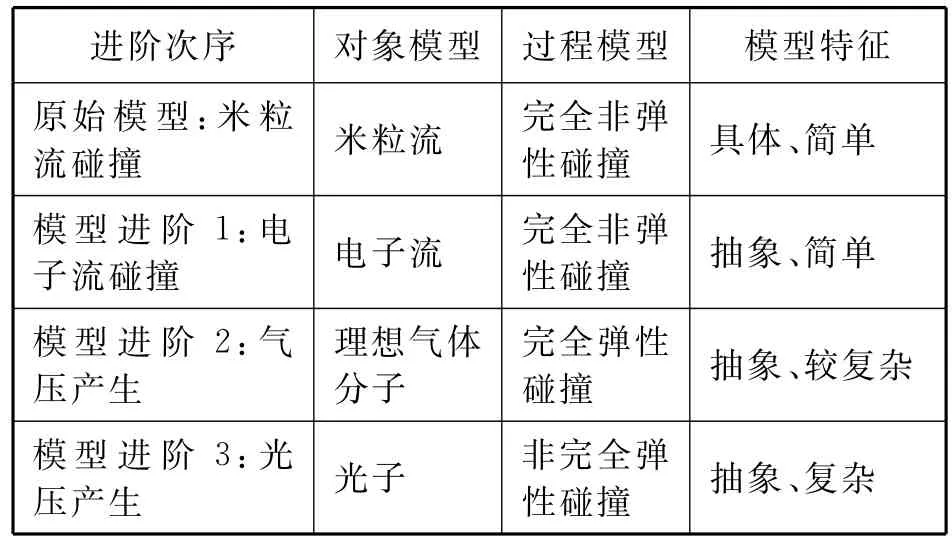
表1 有关连续体碰撞的模型进阶
1 原始模型:米粒流碰撞模型
米粒流撞击台秤产生示数的现象在生活中较为普遍、易于联想.米粒流碰撞模型是一类经典的连续体碰撞模型,以此模型作为进阶的起点.类似的问题情境还有水流等流体产生的冲击力.
例1.如图1,利用自动称米机称米,买者认为:因为米落在容器中有向下的冲力,造成读数偏大,因而不划算;卖着认为:当读数满足需求时,自动装置立即切断米流,尚有一些米在空中,这些米是多给买者的,因而买家赚了.自动称米机究竟准不准?说说你的看法.
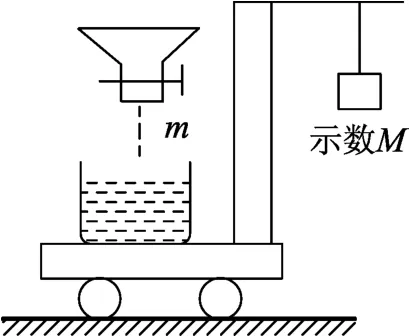
图1
解析:问题的争议主要在空中的米流柱的末端对台秤造成的冲击力,是否与空中米流柱的总重力相同.可以运用“微元法”,选取空中米流柱底端的一小部分Δm,设该米流微元对台秤造成的冲击力大小为F、与台秤作用时间为Δt、自由下落高度为h,由于米流撞击袋子中的米堆不会反弹,因此该米流微元与米堆发生完全非弹性碰撞,根据动量定理可以得到

该米流微元落到米堆时的速度v满足

设米粒流的流量为ρ(单位时间内流出的米流质量),则ρ=Δm/Δt,结合(1)、(2)两式可以得到米流柱底端撞击台秤产生的冲击力
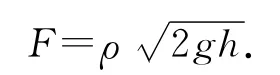
空中米流柱下落时间t满足

空中米流柱总质量m′满足

空中米流柱总重力G′满足
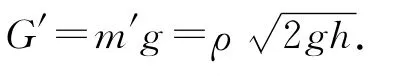
可见F=G′,说明空中米流柱底端对台秤的冲击力示数与空中米流柱自身重力相同,因此自动称米机是准确的,买家不赚卖家不赔.
实验验证:如图2,打开龙头让水流出,用电子秤测量流进烧杯中的水的质量,通过拍摄视频可以发现,在关闭龙头时空中仍然存在一段水柱,此时电子称示数为90g,如图2(甲)所示.当空中的水柱落回烧杯后,此时电子秤的示数仍然为90g,如图2(乙)所示.通过该实验现象可以说明空中水柱底端对台秤产生的示数与这段水柱的总重相同.

图2
2 模型进阶1:电子流碰撞模型(由米粒流到电子流的对象模型进阶)
金属中电流的产生是电子定向移动形成的,电子流撞击金属片可形成电流.电子流碰撞模型是米粒流碰撞模型的对象模型进阶,该对象模型抽象,需要由米粒流进行类比迁移,但由于其过程模型仍然是完全非弹性碰撞,因此在运用动量定理分析此类问题并不复杂.
例2.(2020年北京高考第19题第2问)如图3所示,真空中有一长直细金属导线MN,与导线同轴放置一半径为R的金属圆柱面.假设导线沿径向均匀射出速率相同的电子,已知电子质量为m,电荷量为e,不考虑出射电子间的相互作用.撤去柱面,沿柱面原位置放置一个弧长为a、长度为b的金属片.在该金属片上检测到出射电子形成的电流I,电子流对该金属片的压强为p,求单位长度导线单位时间内出射电子的总动能.
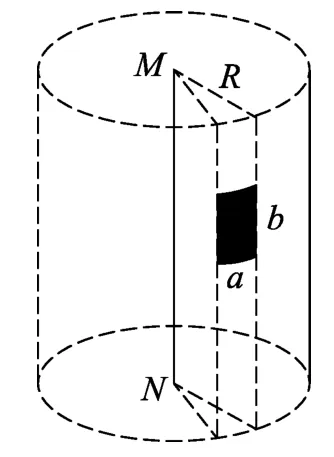
图3
解析:假设单位时间内金属片接收到的电子个数为n,电子射出的速度为v0,电子流对金属片的作用力大小为F,根据动量定理

电子流对金属片产生的压强可以表示为

金属片上检测到的电流可以表示为

联立(6)、(7)式得到

若将该金属片沿弧长a延展至一周(宽度b不变),则金属片单位时间接收到的电子个数

则单位长度的导线单位时间射出电子个数

联立(8)-(10)式,得到单位长度导线单位时间射出电子总动能
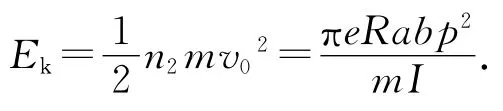
3 模型进阶2:气压产生(由电子气到气体分子、由完全非弹性碰撞到完全弹性碰撞)
与电子流的定向运动不同,理想气体分子向空间各个方向运动的几率相同,存在朝某一方向做定向运动的概率.理想气体分子碰撞模型不仅存在对象模型的进阶、还存在这过程模型的进阶,即研究对象是以一定概率做定向运动的气体分子、而且碰撞过程是完全弹性碰撞具有反弹速度,因此运用动量定理分析此类问题较为复杂.
例3.(2013年北京高考第24题第2问)正方体密闭容器中有大量运动粒子,每个粒子质量为m,单位体积内粒子数量n为恒量,为简化问题,我们假定:粒子大小可以忽略;其速率均为v,且与器壁各面的碰撞机会均等;与器壁碰撞前后瞬间,粒子速度方向都与器壁垂直,且速率不变.利用所学力学知识,导出器壁单位面积所受粒子压力f与m、n和v的关系.
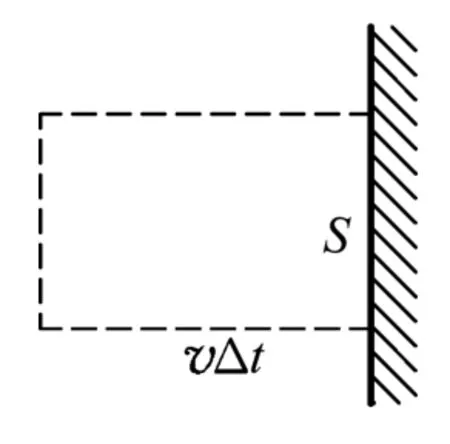
图4
解析:由于理想气体分子和器壁发生完全弹性碰撞,分子碰后速度与碰前速度等大反向,根据动量定理,单个分子动量变化量的大小满足

为计算Δt时间内撞击器壁的分子个数,构建如图4所示的立方体模型,如果气体分子均撞向器壁,撞击器壁的分子个数可以表示为vΔtSn,由于分子朝各个方向运动的几率相同,即朝前、后、左、右、上、下的运动几率相同,因此实际的分子个数可以表示为

根据动量定理,器壁受到的撞击力大小F满足

由此解得

最后得到气体分子撞击器壁产生的压强,即气体压强满足

延伸思考1.假设气体分子与缸壁的碰撞视为弹性碰撞,气体分子的质量为m,温度为T时气体分子的速率为v,且与缸壁碰撞前后,速度方向均与缸壁垂直.若该温度下单位时间内气体分子与缸壁单位面积碰撞次数记为N,请导出此温度下的压强p与m、v、N之间的关系.
解析:根据动量定理
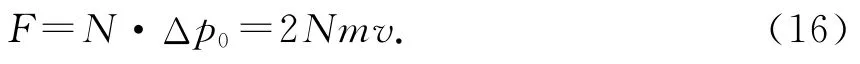
根据压强的定义进一步得到

延伸思考2.例3中的n的含义是单位体积内的气体分子个数,而例4中的N是气体分子与缸壁单位时间、单位面积碰撞次数,两者之间存在怎样的关系?
延伸思考3.(由2019年北京高考第24题第3问改编)由于大量气体分子在各方向运动的几率相等,其对静止雨滴的作用力为0.将雨滴简化为垂直于运动方向面积为S的圆盘,推导圆盘以速度v下落时,受到的空气阻力所满足的关系.(提示:设单位体积内空气分子数为n,空气分子与圆盘碰撞前后相对圆盘的速度大小不变且均为u,且u>v,单个空气分子质量为m0).
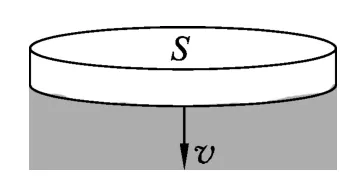
图5
解析:以地面为参考系,以竖直向下为正方向,单个分子碰撞前后动量的变化量
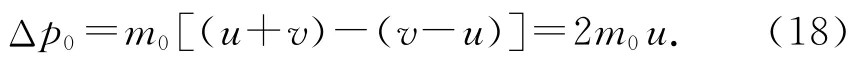
Δt时间内与雨滴碰撞的气体分子个数表示为

根据动量定理得到

联立(18)-(20)式得到
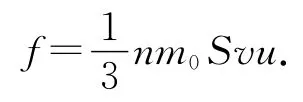
4 模型进阶3:光压产生(由气体分子到光子、由完全弹性碰撞到非完全弹性碰撞)
光子碰撞物体表面同样会产生压强,即光压.黑色物体能完全吸收光子,因此光子与黑色物体的碰撞是完全非弹性的,而白色物体完全反射光子,因此光子与白色物体的碰撞是完全弹性的,一般物体存在部分吸收光子的情况,即光子与物体的碰撞一般认为是非完全弹性的,这使得连续体碰撞的过程模型变得复杂.
例4.根据量子理论:光子既有能量也有动量;光子能量E和动量p之间的关系是E=pc,其中c为光速.由于光子有动量,照到物体表面的光子被物体吸收或被反射时都会对物体产生一定的冲量,也就对物体产生了一定的压强,称之为“光压”(类比“气压”).根据动量定理可以近似认为:当动量为p的光子垂直照射到物体表面,若被物体反射,则物体受到的冲量大小为2p;若被物体吸收,则物体受到的冲量大小为p.
某激光发出激光束的功率为P0,光束的横截面积为S.当该激光束垂直照射到某物体表面时,物体对该激光的反光率为η,请推导该激光束对此物体产生的光压大小.
解析:设时间Δt内,照射到物体表面的光子个数为N,依题意得

由于一部分光子发生完全弹性碰撞、另一部分光子发生完全非弹性碰撞,因此光束与物体的碰撞属于非完全弹性碰撞,根据动量定理得到物体受到的撞击力F大小满足
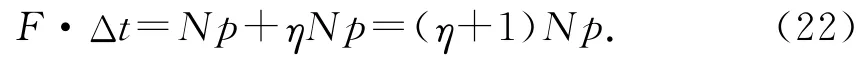
联立(21)、(22)式得到
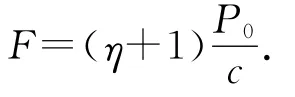
激光束对此物体产生的光压大小为
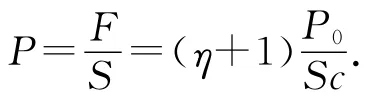
5 结语
连续体碰撞问题包含了牛顿运动定律、动量定理等运动和相互作用观,模型建构、推理论证等科学思维要素,以及“微元法”等物理学科方法;解决此类问题往往需要学生具备较高的物理核心素养和高阶思维.根据从感性到理性、从具体到抽象、从简单到复杂的认知进阶规律,教师可以从原始的连续体碰撞模型出发,引导学生亲历从连续体(如米粒流)到电子流、理想气体分子、光子的对象模型进阶,从完全非弹性碰撞到完全弹性碰撞、非完全弹性碰撞的过程模型进阶.通过物理模型进阶,辅助学生熟悉并掌握连续体碰撞问题.
