强磁场对中子星转动惯量与表面引力红移的影响*
2021-12-09赵诗艺刘承志黄修林王夷博许妍
赵诗艺 刘承志† 黄修林 王夷博‡ 许妍††
1) (中国科学院国家天文台长春人造卫星观测站,长春 130117)
2) (中国科学院大学天文与空间科学学院,北京 100049)
开展强磁场环境下中子星物质性质的研究对约束中子星物态方程,揭示星体内部磁场分布形式等有重要意义.本文基于相对论平均场理论利用GL91 参数组研究了处于β 平衡条件下传统中子星物质在强磁场作用下的主要宏观性质.结果表明,强磁场的引入使传统中子星物态方程变硬,星体质量上限由2.111 M⊙增大到3.081 M⊙,相同质量星体对应的半径变大使星体变得不那么致密;强磁场对传统中子星表面引力红移有抑制作用,对转动惯量有促进作用.此外,给出了目前已观测到的四颗大质量脉冲星—PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135,以及双星合并事件GW190814 中质量在2.50 M⊙—2.67 M⊙的致密星体表面引力红移和转动惯量的理论值范围.结果表明,随着中子星内部磁场的增强,这五颗星的表面引力红移值范围变窄,而转动惯量的范围变宽.
1 引言
中子星内部结构的研究是当前中子星理论与观测研究中的难点问题之一,现阶段很难通过直接手段获得中子星内部结构的详细信息,需借助唯象或微观核多体模型结合天文观测约束星体物态方程 (equation of state,EOS) 进行研究.中子星EOS 是描述物质在一定物理条件下状态的热力学方程,表示星体内部压强和能量密度的关系.中子星EOS 包含了星体内部结构的大量信息,是连接中子星内部结构和宏观物理性质的一个重要桥梁,通过中子星EOS 可以获得星体的质量、半径、转动惯量和表面引力红移等宏观物理量.
脉冲星质量测量是约束中子星EOS 最常见的方法.目前中子星内部成分探测器 (NICER) 已公布的具有可靠质量的脉冲星样本仅有100 多颗[1],其中只包含一颗孤立中子星 (PSR J0030+0451)的质量和半径测量值,其质量为或对应的半径为和脉冲星的质量和半径,尤其是半径不容易测量,因此,人们希望找到脉冲星质量和半径之间存在的某种关系.脉冲星转动惯量和源于星体表面辐射谱线的引力红移是与星体质量、半径都相关的物理量,相较于脉冲星半径,星体质量、转动惯量和表面引力红移易于测量.如果天文观测获得了一颗脉冲星质量和转动惯量或者质量和表面引力红移测量值,就可以估算出这颗星的半径.因而测量脉冲星转动惯量和星体表面辐射谱的引力红移已成为约束中子星EOS 的重要补充条件[3−5].学者们针对中子星转动惯量和表面引力红移与中子星内部结构关系开展了许多意义深刻的工作.如2001 年,彭芳等[6]研究了中子星转动惯量、表面引力红移与核物质不可压缩系数和对称能强度的关系,分析了奇异介子对PSR J0348+0432 表面引力红移和转动惯量的约束.2010 年,赵先锋和张华[7]研究了奇异介子对前身中子星转动惯量的影响.2020 年赵先锋[8]研究了超子耦合参数对中子星引力红移的影响.2019 年,Lim 等[9]在手征有效场理论和有限核物质性质约束下基于核能密度泛函的贝叶斯分析计算了PSR J0737-3039A的转动惯量.2020 年,Sen[10]利用中子星物质有限温度EOS 分析了温度对星体表面引力红移的影响.
脉冲星表面偶极磁场强度可以直接由星体自转周期及自转周期导数给出,而脉冲星自转周期及自转周期导数一般通过天文观测可直接获得,因此脉冲星表面偶极磁场强度较易测量,并已成为约束中子星EOS 的有效方法.天文学家发现中子星表面磁场在1011—1013G (1 G=10–4T),如目前已知中子星X 射线双星系统中磁场最高的是Be/X 射线瞬态脉冲星GRO J1008-57,其表面偶极磁场B ≥6×1012G[11];磁星,其候选体为软γ 射线重复暴或反常X 射线脉冲星,研究表明其表面偶极磁场高达1014—1015G[12,13];此外,根据位力定理,中子星内部磁场甚至可能高达1018G[14,15].近年来,学者们基于脉冲星表面偶极磁场强度测量数据建立了多种中子星辐射模型,围绕中子星磁场与星体的内部结构、EOS、星体热演化过程、磁场演化、磁星结构等方面开展了深入丰富的研究,获得了丰硕的成果[16−25].然而强磁场环境下中子星转动惯量和表面引力红移的研究相对很少.
因此,本文在相对论平均场理论(relativistic mean field theory,RMFT)框架下利用GL91 参数组给出强磁场环境下传统中子星EOS;通过求解广义相对论流体静力学平衡方程(Tolman-Oppenheimer-Volkoff,TOV 方程),得到了强磁场对传统中子星表面引力红移和转动惯量的影响;同时将不同磁场强度下的理论结果和当前的观测数据进行了对比.此外,基于四颗大质量脉冲星PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135 和引力波信号GW190814 所包含的致密星的质量测量值的约束,给出了这五颗星表面引力红移和转动惯量的理论值范围.
2 理论基础
2.1 强磁场环境下的RMF 理论模型
本文主要讨论由核子(n,p)、轻子(e,µ)组成的传统中子星,记作npeµ物质.强子之间的相互作用由介子(σ,ω,ρ)来传递.强磁场环境下,中子星物质的拉格朗日密度为
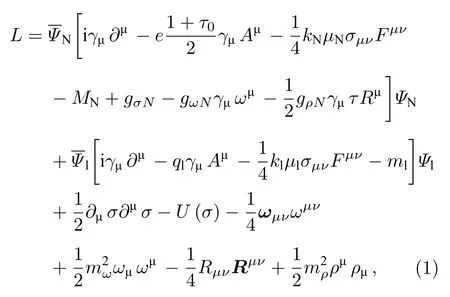
其中U(σ)是σ 场的非线性自相互作用项,具体形式如下[26]:

ΨN代表核子的Dirac旋量,Ψl代表轻子的Dirac 旋量.τ 是核子同位旋,τ0是它的第三分量;ωµν,Rµν为ω,ρ 介子的场张量;Aµ≡ (0,0,Bx,0)表示磁场.MN是核子的质量;ml是轻子的质量;mσ,mω和 mρ分别是σ,ω 和ρ 介子的质量;gσN,gωN,gρN分别是σ,ω,ρ 介子与核子之间的耦合常数;kN,kl为核子和轻子的反常磁矩系数;µN为核子的核磁子,µl为轻子的玻尔磁子.本文采用GL91 参数组[27]来描述强磁场下中子星物质整体性质,具体取值如下:MN=939.565 MeV,mσ=550 MeV,mω=781.9 MeV,mρ=769 MeV,gσN=8.7818,gωN=8.7116,gρN=8.4635,g2=27.9060,g3=–14.3989.结合能E/A=16.3 MeV,饱和密度ρ0=0.153 fm−3,对称能 αsym=32.5 MeV.
把(1)式代入Euler-Lagrange 方程,可以得到核子在磁场中运动的Dirac 方程以及三种介子场的运动方程:
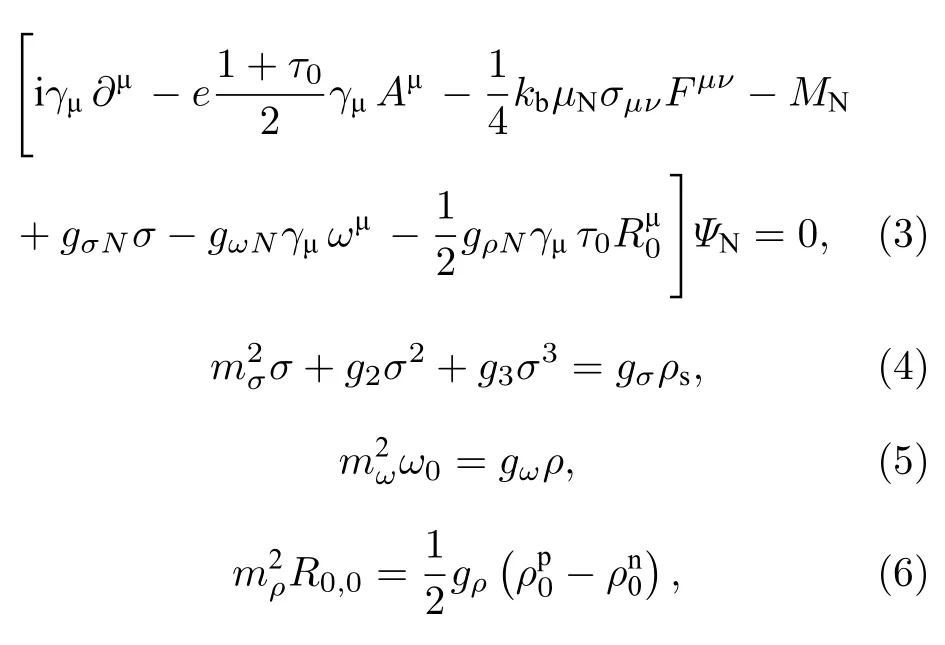
其中 σ,ω0,R0,0分别是三个介子场场量的基态期待值;为标量场密度,为核子数密度.中子星物质应满足β 平衡和电中性条件[28],β 平衡条件如下:

其中各组分化学势的具体形式如下:

它们与各自费米动量的关系如下:

电中性条件为


此外,体系中电子、μ 子的密度与费米动量的关系为:

在(17)式—(22)式中,对 ν 的求和从其最小值开始,随着ν的增加直到ν 的某一特定最大值,且当ν 取该值时,的值为正.对于自旋向上的质子,对 ν 的求和从1 开始,对于自旋向下的质子对ν 的求和从0 开始.需注意此处的自旋方向只是相对概念,因为波函数不再是自旋算符三分量的本征波函数,而是与磁场耦合的自旋密切相关.
至此可以求得传统中子星物质各组分的能量密度:

从而可以得到中子星物质能量密度如下:

其中 ϵn,ϵp,ϵe,ϵµ分别代表n,p,e 和µ粒子对能量密度的贡献.
再考虑电磁场对能量密度的贡献[29],可以得到传统中子星物质总的能量密度和压强:

2.2 TOV 方程
在中子星性质的研究中,常常需要计算一些能够表征星体性质的宏观量与脉冲星观测数据进行对比,因而仅有星体EOS 是不够的,需要借助表达中子星结构的TOV 方程来研究星体的宏观性质,具体形式如下[30,31]:
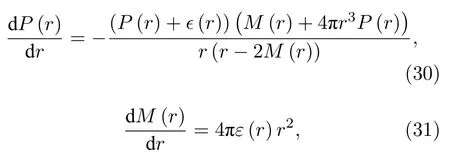
其中r,M(r),ϵ(r),P (r) 表示中子星的半径、质量、能量密度、压强.可见,以EOS (28)式和 (29)式作为输入量,在边界条件P (R)=0,M(0)=0下,可以获得TOV 方程的解,即强磁场环境下中子星的质量-半径关系.
2.3 中子星的转动惯量和引力红移
慢旋转条件下的中子星在球坐标系(t,r,θ,Φ)中的时空度规可以表示为
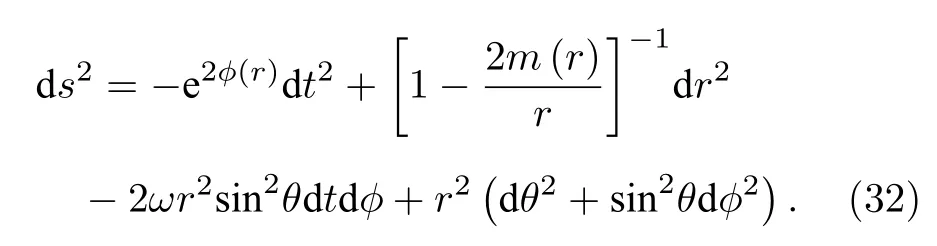
中子星的转动惯量在低阶近似下由以下公式给出[32]:

其中 Ω 表示星体的角速度,ω 为一个遥远0 角动量观者观测到的角速度,ϖ=Ω−ω 为坐标拖曳角速度.Φ(r) 和 ϖ(r) 由以下公式给出:
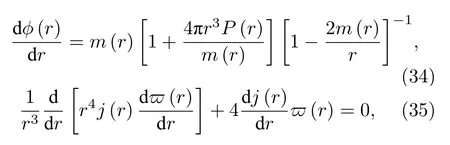
其中
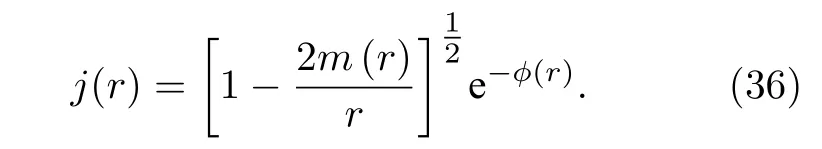
通过(36)式—(36)式可获得中子星的转动惯量,而对于质量大于1 M⊙的中子星,Lattimer 和Schutz[33]发现转动惯量的表达式(33)式可以由下面的经验公式很好地描述:

在中子星表面,由于光子逃逸时需要克服引力场做功,因此会导致光子能量减少,从而使观测到的光谱频率降低,由此产生的效应称为引力红移.广义相对论给出了中子星表面引力红移的计算公式[34]:
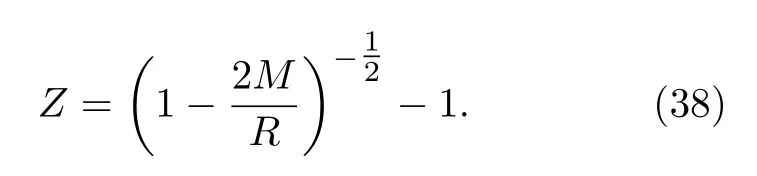
可见,通过中子星质量M 和半径R 可获得星体转动惯量和表面引力红移的理论值.
2.4 中子星内部磁场分布
鉴于中子星内部磁场分布仍是未知的事实,本文采用目前被广泛应用的一种从表层到中心随密度变化的中子星内部磁场模型,其具体形式如下[21,35,36]:

声速可以反映EOS 硬度和物质不可压缩性等信息,是研究中子星结构的重要工具,本文以中子星物质声速为约束条件对星体内部磁场强度进行约束,受因果关系限制,中子星物质的声速vs不应超过光速c[39],声速的表达式为

可见,以中子星EOS 作为输入量可以获得星体的声速值.
3 中子星宏观性质及数值结果
四颗约2 M⊙质量的脉冲星相继被发现,为大质量中子星的存在提供了强有力的验证[40−45].此外,2019 年,LIGO/Virgo发现双星合并引力波信号GW190814,认为其中应该包含质量为2.5—2.67 M⊙的致密星体,它或者是一颗大质量中子星或者是一颗小质量黑洞[46],引力波探测并没有揭示它的性质,而如果确定这颗致密星体是中子星将使中子星理论模型受到极大的挑战(本文将GW190814 中致密星假设为一颗脉冲星进行讨论).
图1 给出了强磁场环境下中子星物质压强随核子密度(曲线(a))、星体质量随半径(曲线(b))的变化.从图1(a)可以看到,无论有无磁场,中子星物质压强都会随着 ρ/ρ0的增加而增加,低密度区域磁场对中子星物质压强的影响非常小;而中高密度区域α 值的增长使得中子星的压强明显变大.RMFT 模型中GL91 参数组对α=0,20,40,60四种情况下获得的中子星最大质量及其所对应的半径、最大半径及其所对应的质量,以及这两种情况下中心密度的计算结果列于表1 中.从图1(b)及表1 可以看到,随着α 的增加,中子星最大质量明显增大(从α=0 时的2.111 M⊙增大到α=60 时的3.081 M⊙),这是因为磁场的引入使中子星EOS 变硬,因此中子星所能对抗的最大引力也会增大;最大半径也有明显增大(从α=0 时的14.014 km 增大到α=60 时的15.765 km).图1(b)还表明,当质量取一定值时α 越大的星体其所对应半径也越大,这表明磁场的引入使中子星变得不那么致密.此外,在图1(b)中用阴影区域表示四颗目前已知大质量PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135 以及引力波信号GW1908 14 所包含的致密星的质量测量值,用橙色误差棒表示PSR J0030+0451 的质量、半径测量值范围.从图1(b)可以看出,强磁场环境下中子星的最大质量满足大质量脉冲星及GW190814 的质量约束且在较低磁场情况下与PSR J0030+0451 的观测值符合良好.如果未来GW190814 中的天体被确认为中子星,那么其磁场相对较强,按图1(b)的数值结果来讲,其中心磁场强度约为8.828×1018G,表面磁场强度约为8.828×1014G.

图1 不同磁场强度下(α=0,20,40,60)中子星物质的(a)压强-核子密度、(b)质量-半径关系.本文中,黑红绿蓝四条线表示α=0,20,40,60 四种情况;不同颜色条纹区域分别表示PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135 以及GW190814 中致密星的质量测量值范围;橙色误差棒表示NICER 公布的PSR J0030+0415 的质量-半径测量值对中子星质量-半径关系的约束.各曲线上黑色圆点表示中子星最大质量所处位置,三角形点表示最大半径所处位置Fig.1.Relationship of (a) the pressure-density and (b) the mass-radius in neutron star (NS) matter.In the paper the black,red,green,and blue lines represent the four cases of α=0,20,40 and 60,respectively.The different colored areas stand for the recent constraints inferred from PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135 and GW190814 respectively.The orange error bar represents the constraints on the mass-radius limits of PSR J0030+0451 obtained from NICER observations.The dots and the triangle points show the maximum masses and radii of NSs for the four cases,respectively.
图2 给出了强磁场影响下中子星物质声速随密度的变化曲线,可以看到,当α=0,20,40 时无论中子星的中心密度多高,声速与光速的比值均小于1.但是当磁场继续增高,如 α 取60 时,声速在中心密度为5.12ρ0时等于光速,而表1 中给出此时最大质量中子星对应的中心密度ρc=2.48ρ0<5.12ρ0.因此本文中α=0,20,40,60 时均满足因果律约束.

表1 不同磁场强度下(α=0,20,40,60),中子星最大质量及其对应半径和中心密度,最大半径及其对应质量和中心密度Table 1.Table 1.Values of the maximum NS masses Mmax and the corresponding radii R as well as the center densities ρc/ρ0,values of the maximum NS radii Rmax and the corresponding masses M as well as the center densities ρc/ρ0 with α=0,20,40,60 in npeµ matter.

图2 不同磁场强度下(α=0,20,40,60),中子星内声速-核子密度关系Fig.2.Relationships of the speed of sound and the nucleon density with α=0,20,40,60 in NS matter.
图3 给出了强磁场作用下中子星转动惯量随质量变化的情况.可以看出,四种情况下质量最大的中子星对应的转动惯量也最大,即Mmax从2.111 M⊙增加到3.081 M⊙,相应的转动惯量从138.253 M⊙km2增加到334.921 M⊙km2,结合图1 的讨论结果,说明越硬的中子星EOS 所对应的星体转动惯量越大.因此,在相同质量条件下,拥有强磁场的中子星转动惯量更大.此外,在图3中标注出了四颗大质量PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135 以 及GW190814中致密星的质量区间,从而在GL91 参数组条件下得到了这五颗星转动惯量理论值的范围,在表2 中列出了具体数值.从图3 和表2 可以看出,随着磁场的增加这五颗星的转动惯量范围变宽.

图3 不同磁场强度下(α=0,20,40,60),中子星转动惯量-质量关系Fig.3.Relationships of the moment of inertia and the mass with α=0,20,40,60 in NS matter.
图4 给出了强磁场影响下中子星的表面红移随星体质量的变化.其中黑框长方形区域表示天文观测给出的脉冲星表面红移值范围,即对于质量处于1.25—1.8 M⊙的脉冲星,其红移值应处于0.25 — 0.35 之间[47].从图4 可以看到,α=0,20,40三种情况下引力红移理论值都与观测数据相符.而α=60 时,由于磁场的增强此时中子星引力红移值与观测数据相比明显偏低.从图4 还可以看出,四种情况下质量最大的中子星对应的星体表面红移也最大,即Mmax从2.111 M⊙增加到3.081 M⊙,相应的表面引力红移从0.462 增加到0.649,这是由于磁场的增强导致星体Mmax/R 比值增加(详情可参考(20)式与表1 的数据).而在相同质量条件下,中子星表面引力红移会随着磁场的增加而减小,结合图2 的数值结果,说明越硬的中子星EOS 给出的中子星表面引力红移越小,这是因为磁场的加入使中子星变得不那么致密,从而使光子在逃逸星体表面时所丢失的能量也会减少,因此导致了引力红移效应的减弱.此外,在图4 中也标注出了四颗大质量PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135 以及GW190814 中致密星的质量区间,从而在GL91 参数组条件下得到了这五颗星表面引力红移理论值的范围,在表2 中列出了具体数值.从图4 和表2 可以看出,随着磁场的增加这五颗星的表面引力红移范围变窄.

图4 不同磁场强度下(α=0,20,40,60),中子星表面引力红移-质量的关系Fig.4.Relationships of the gravitational redshift and mass with α=0,20,40,60 in NS matter.

表2 不同磁场强度下(α=0,20,40,60),PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135 以及GW190814中致密星的半径、转动惯量、引力红移理论值范围Table 2.Ranges of the theoretical values for the radius,the moment of inertia and the gravitational redshift corresponding to PSRS J1614-2230,J0348+0432,J0740+6620,J2215-5135 and the compact star in GW190814 with α=0,20,40,60.
综上,计算出的中子星转动惯量、引力红移在α=0,20 时与天文观测数据符合较好,而α=40 时,理论曲线恰好处于观测数据范围的边缘附近,因此我们考虑这是GL91 参数组下,中子星磁场强度所能达到的上限.α=40 所对应的表面磁场约为1.766×1015G,与当前磁星表面磁场强度的大小基本符合,中心磁场约为1.766×1019G,比位力定理给出的数值略高[1,2].未来中子星转动惯量、表面引力红移等天文观测数据的增多,将有助于进一步限制强磁场下中子星EOS,并有望揭示星体内部组成.
4 结论
本文在RMF 理论框架下采用GL91 参数组系统研究了强磁场对传统中子星宏观性质的影响.结果表明,磁场增加会导致中子星EOS 变硬,使星体所能达到的最大质量、最大半径均增加,并且使中子星变得不那么致密.中子星EOS 决定了星体的M-R 或M/R 的值,因而强磁场也对中子星表面引力红移与转动惯量有显著影响.从整体上来看,中子星表面引力红移与转动惯量都较强地依赖于中子星内部的磁场强度.强磁场对中子星引力红移有抑制作用,但是会增大最大质量中子星所能达到的引力红移理论值;对中子星转动惯量有促进作用,会显著增大最大质量中子星转动惯量理论值.此外,对于PSRs J1614-2230,J0348+0432,J0740+6620,J2215-5135 以及GW190814 中致密星而言,磁场的增加会使它们的引力红移范围变窄,而转动惯量范围变宽.随着我国大型射电望远镜陆续投入使用,期待未来可以利用更多天文观测数据来约束中子星理论模型.这将对揭示中子星内部磁场的分布形式以及星体内部组成的研究提供有益的参考.
