地球流体动力学模型恢复的长短期记忆网络渐进优化方法

Gary Yen，栗 波，谢胜利

（1. 美国俄克拉荷马州立大学 电气与计算机工程学院，俄克拉荷马州 静水 74078；2. 广东工业大学 自动化学院，广东 广州 510006）

从太空卫星到社交媒体聊天，从信用卡交易业务到医疗保健记录，都得益于先进的传感技术、强大的计算平台和广泛的在线连接技术，日益增加的数据量极大地改变了现代处理和分析数据的计算和统计方法。与此同时，基于人工智能和机器学习的数据分析开始在推进科学发现和工程设计方面发挥出重要作用。过去，科学的进步是先提出假设，然后收集数据来证实或否定这些假设。然而，在大数据时代，虽然数据被收集了起来，却对其内部运作一无所知，导致形成了所谓的黑箱解决方案。这种观点根本不正确：海量数据可以使得在没有科学理解的情况下建立可操作的模型成为可能。理想情况下，将挖掘的模式信息和内在关系转化为可解释的理论和假设，从而推动科学认知的进步，这才是最重要的。因此，即使黑盒模型在特定的空间、时间和频谱情景下实现了某种程度的精确性能，但仍缺乏对底层演变过程作用机理的理解能力，也就不能可靠地成为后续科学和工程发展的基础。这一点尤其适用于当今地球物理流体动力学或热动力学领域。地球物理流体动力学，广义上说，指的是在地球和其他行星上自然发生的流动(例如熔岩流、海洋和行星大气流)的流体动力学。

在工程设计、控制和建模中，存在着各种各样的任务都需要求解基于偏微分方程(Partial Differential Equation, PDE)的多集合前向模型。例如，在顺序数据同化中，前向模型的多个集合被用来逼近协方差矩阵[1]。随着所需精度要求的提高，时空数值模拟离散化的粒度也需要适当提升。这将导致计算工作量的显著增加，并可能成为设计和预测周期的外部循环中的瓶颈。例如，在计算流体力学(Computational Fluid Dynamics, CFD)中，湍流的三维模拟[2]常被用于获得Navier-Stokes方程的精确解，但在形状优化等相关任务中却使用得较少[3]。因此，建立一个计算代价比全阶模型(Full Order Models, FOM)更低的降阶模型(Reduced Order Model, ROM)，并提供足够精度水平的解决方案的研究得到了很多人的关注[4-6]。

近年来，人们对开发用于物理系统的非侵入式ROM的研究兴趣与日俱增[7-9]。“非侵入式”指的是只通过数据来构造降阶模型。非侵入式降阶模型特别适用于理想模型未知，但存在大量数据可用于模型恢复的系统。这种情况在地球物理流体中非常普遍。由于网格分辨率不足而导致的子网格尺度的近似、模型参数的不确定性或模型本身结构不正确等原因，使得地球物理系统模型可能是不完善的[10]。然而，从遥感、卫星观测和地球物理流体实验测量中已经获得了大量的实测数据。因此，为了有效地预测地球物理过程，利用这些数据已经开展了多项研究[11-12]。

在本研究中，主要使用线性降维技术并配合机器学习算法来演化隐空间[13-14]。具体来说，就是利用本征正交分解(Proper Orthogonal Decomposition,POD)来识别全阶模型的隐空间，然后利用长短期记忆(Long Short-Term Memory, LSTM)神经网络来模拟隐空间的演化过程。这种替代建模技术的主要优点之一是它由纯数据驱动，因此特别适合地球物理流体的研究数据集。利用遥感和现场观测收集的档案数据建立替代模型，然后将替代模型用于完成预测任务。当获得新数据之后，可以使用迁移学习方法[15]重新训练替代模型，从而提高预测精度。

除了ROM之外，神经网络在许多科学研究中的使用也显著增加[16-17]。神经网络的主要挑战之一是其性能过于依赖其网络结构[18]。此外，神经网络包含大量与问题相关的超参数。通常，人工神经网络是通过试错法来设计的，这一过程可能相当耗时。此外，要获得良好的性能，还需要设计者具有深刻的数据理解和丰富的神经网络领域知识。虽然有诸如“网格搜索”或“随机搜索”这样的方法来找到超参数的优化组合，但是随着搜索空间的维数增加，这些方法的可扩展性欠佳。因此，人们对神经网络结构和超参数搜索的自动化设计相关的内容越来越感兴趣，这将允许那些没有神经网络专业知识的用户可以将其应用于他们感兴趣的特定研究问题[19]。本文采用遗传算法对LSTM神经网络的结构设计和超参数进行优化。将LSTM网络用于NOAA海表温度数据集的替代模型设计。

本文其余部分的结构如下。首先，在第1节描述了非侵入式降阶模型的建模方法和数据预处理。然后，在第2节中给出了所提出算法的细节。第3节讨论了实验结果及其分析。最后，在第4节中，对本文的结论和未来的研究方向进行了展望。

1 非侵入式降阶模型

1.1 本征正交分解

本文使用POD来提取表征上述非线性动力系统的主导模式。在不同的时刻收集了(动态网络的)数据快照u1,u2,···,uN∈RM，其中M为空间自由度，N等于网格点总数，为数据快照的个数。利用本征正交分解，本文构造了一组标准正交基函数来优化描述系统的场变量。则快照的数据矩阵形式如式(1)所示。

1.2 ROM的无模型演化

特别是在地球物理动力系统中，ROM演化的无模型预测具有广阔的应用前景。对于各种各样的任务，如数据同化和地球物理流体的不确定性量化，需要运行前向模型的集合，伴随着巨大的计算代价。可以使用基于ROM的替代模型来取代前向模型的演化过程。对于许多地球物理动力系统，由于网格分辨率颗粒度较为粗糙，动力系统的力学描述是不可用的或不足的。然而，在过去的几十年里，从局部和卫星观测中获得了大量的数据，数据驱动的方法如递归神经网络(Recursive Neural Network, RNN)在时空混沌动力系统的无模型预测中被证明是成功的[22-23]。

式(4)中的时变模态系数是通过在POD基础上的投影平均值减去场能求得的，如式(5)所示。

1.3 数据预处理

无模型预测对于现实世界的实测数据尤其重要，因为实测数据是由多尺度过程产生的，这些过程不能用任何基于模型的方法精确地逼近。现实世界中的流体动力过程是由多个外部系统耦合控制的，而这种耦合可能是未知的或无法建模的。因此，现有模型对现实世界中的数据描述效果欠佳，非侵入式方法则非常适合这些复杂的流体。为此，本文研究了非侵入式降阶模型在NOAA最优差值海表温度数据集(第2版)上的应用。该数据集由一个分辨率为1°的网格上的每周平均海表温度数据快照组成，并结合卫星和本地测量生成。季节性波动使得该数据集的温度场具有很强的周期性结构。

沿纬度和经度以1°作为网格分辨率，数据集的每个快照的维数为180×360。利用掩模运算去除与陆地相对应的数据点，并建立了仅针对海洋表面的归一化数据的替代模型。该数据的时间跨度为1981年10月22日至2018年6月30日(即共1 914个快照)。

数据预处理完成后，利用去均值(异常)场的温度数据生成快照数据矩阵。ROM的模式数量是根据式(6)所示的相对信息含量(Relative Information Content,RIC)求得

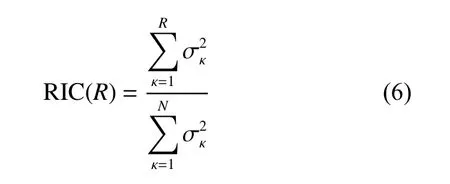
RIC表示可使用R基函数恢复的总体数据的信息(方差)比例。图1显示了NOAA最优差值海表温度数据集的RIC百分比。本文将保留模式的数量固定为R=8，它捕获了约92%的数据信息(方差)，并且这些模式足以捕获NOAA数据集中的季节趋势。可以看出，在8个模式之后，模式数量的增加使得总信息方差的增加非常小，这是由于这些模式主要负责捕捉小尺度的波动。

图1 快照数据矩阵 A的奇异值平方百分比(相当于AAT 或AT A的特征值)，ROM的保留模式数为8Fig.1 Percentageof the squareofsingular valuesofthesnapshot data matrix A(equivalenttoeigenvalues ofAAT orAT A). The number of retained modes for the ROM is 8

2 LSTM的遗传算法优化

神经网络的性能在很大程度上依赖于神经网络结构的设计和其他超参数的选择，例如激活函数、优化器、初始权重值等。类似于其他超参数优化的研究[28-34]，本文使用不同类型的小型结构对整个LSTM架构进行编码。图2展示了作为LSTM主体网络组成构件的不同类型的小型体系结构。在这些小型结构中，每一个都采用了残差连接，因为它允许训练深度神经网络，而不会导致梯度消失的问题[35-36]。最终的LSTM网络是通过对这些组件进行排序来构建的。LSTM存储单元数和模块层数是与使用遗传算法优化的神经网络结构设计相关的另外两个参数。需要优化的其他超参数包括优化器的类型、优化器的学习率、权值和偏差的初始化分布以及激活函数。

图2 LSTM网络的组成构件的不同类型的编码小型组件Fig.2 Different types of encoded small architectures act as the building block of entire LSTM architecture

算法1列出了本文所提框架的伪代码。它首先初始化指定大小的填充。根据预定义的组件构造个体的LSTM子网络，并在此基础上分配其他超参数。在训练数据集上采用三重交叉验证对神经网络进行评估。一旦计算出种群中每个个体的适应度(即，本研究中的验证均方误差)，就会根据适应度值对个体进行排序。在这个种群当中，保留一定比例的精英个体(作为亲本)，通过联赛选择算法竞争产生下一代个体。利用交叉和变异算子从选择的双亲中产生子代个体。新种群是由老种群中保留下来的精英个体与子代个体结合而成的。因此，新种群是由前一次迭代的精英个体和新产生的子代组成的。增加遗传代数计数器，并在给定的指定遗传代数内重复上述过程。

算法1 本文提出的遗传算法

输入: 一组预定义的构件，种群规模，最大遗传代数Ng，训练数据集，精英保留百分比。

输出: 找到的LSTM网络结构以及其他超参数。

1.P0←以给定规模初始化种群；

2.k←0；

3. 从k=0到最大遗传代数，循环以下操作：(for循环)

4. 计算种群当中每个个体的适应度Pk;

5.PkE←保留具有最大适应度值的精英群体;6.PTk←使用联赛选择法挑选产生子代种群的亲本个体；

7.Qk←使用本文提出的交叉和变异算子从所选亲本当中产生后代个体；

8.Pk+1←PkE∪Qk；

9.k←k+1；

10. 结束循环。

11. 返回种群Pk产生的适应性最好的个体。

使用7个整数来定义种群中的每个个体。这些数字代表了LSTM网络的超参数。这些超参数的上、下限以及用于生成这些数字的分布类型参见表1。第1个参数是网络的组块(数量)，图2展示了4种不同类型的可用于设计LSTM网络的组块结构。第2和第3个参数与LSTM网络的深度(即隐藏层的数量)和宽度(即LSTM的cell单元的数量)有关。其他参数如激活函数、优化器、学习率、初始权重值等都与LSTM网络的训练有关。在评估过程中，针对每个个体对应的LSTM网络进行训练，并将验证均方误差(Mean Squared Error, MSE)作为该个体的适应度。种群根据适应度值按升序排序(MSE越低，适应度越好)。

表1 LSTM网络的超参数Table 1 Hyper-Parameters of the LSTM Network

下一步是为子代个体选择亲本。本文采用联赛选择算法来挑选亲本。算法2给出了联赛选择算法的选择过程。在联赛选择过程中，从种群中随机抽取少数个体，选出其中的最佳个体用于产生子代。

5. 结束循环。

6. 返回选取的种群PTk。

3 实验与分析

在本节中，给出了遗传算法在优化神经网络结构设计和超参数方面的结果。然后，展示了优化后的LSTM网络在NOAA数据集仿真和预测中的性能。

NOAA数据集的时间跨度为1981年10月22日至2018年6月30日，对应1 914个样本快照。本文利用前1 500个数据快照中随机选择的70%样本数据作为训练数据集。在LSTM网络的超参数优化过程中，对种群内的个体进行了100个epoch的训练(一个epoch即是将所有训练样本训练一次的过程，epoch数为100)，并采用三次交叉验证来避免过拟合。将LSTM网络的回溯时间窗口的步长设置为8，用于捕捉模态系数之间的时间相关性。每个个体的适应度是三折交叉验证数据集的MSE的平均值。一次训练所选取的样本数(Batch Size)固定为64。本实验的种群规模和遗传代数设置为20。图3展示了种群内个体适应度随遗传算法的遗传代数的演化轨迹。箱线图用于显示每一代的种群统计数据。图3还呈现了每一代种群数量的MSE的中位数和最小值。随着演化过程的进行，验证集上的均方误差也逐渐减小。矩形盒的高度表示种群在每一代的适应度的方差，可以看出，第一代之后的方差显著降低。MSE从第一代到第二代急剧下降，这可以归因于遗传算法开始时种群的随机初始化。对于本文中所研究的问题，3～10代(遗传代数)似乎就足以找到最佳的超参数集。

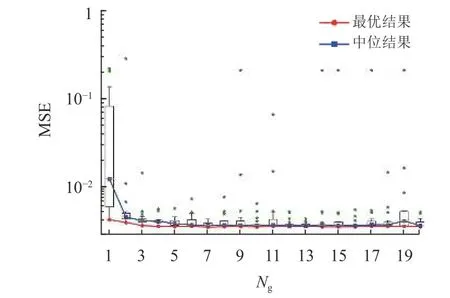
图3 本文提出的算法在NOAA海温数据集上探究LSTM网络最佳结构的演化轨迹Fig.3 The evolutionary trajectory of the proposed algorithm in discovering the best architecture of the LSTM on the NOAA SST data set

利用遗传算法找到最优网络结构和其他超参数后，对最优LSTM网络进行了1 200个epoch(即1 200次遍历整个训练数据集)的训练，批量大小(一次训练的样本数)为64。在训练后的网络部署过程中，采用自回归法对模态系数进行预测。给出了前8个时间步(等于LSTM的回溯时间窗口长度)模态系数的初始条件。该信息用于预测第9个时间步的模态系数。然后利用第2到第9个时间步的模态系数来预测第10个时间步的模态系数。重复此过程直到最后一个时间步，即第1 914个时间步。由于本文自回归部署使用的是经过训练的LSTM网络，所以只需要设置LSTM回溯所对应的初始条件。在经过(初期的)几个时间步后，仅利用LSTM的预测结果作为未来(时间步)的模态系数预测值。图4展示了模态系数的真实值和预测值。可以看出，尤其对于负责捕捉大尺度波动和季节模式的前几个模态而言，它们的模态系数的真实值和预测值之间具有良好的一致性。

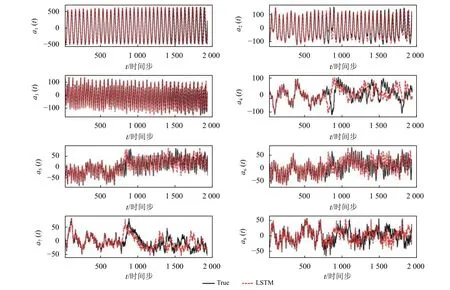
图4 利用本文提出的遗传算法发现的最佳LSTM网络对模态系数进行时间序列预测Fig.4 Time series prediction of the modal coefficients with the best LSTM network discovered by the proposed GA algorithm

图5描绘了两个不同时刻的真实温度场和重建温度场。利用式(4)重建温度场，其中平均温度场是由前1 500个数据快照计算所得。基于LSTM的ROM(降阶模型)能够准确地捕捉温度场中的大尺度模式，展现出数据驱动的ROM在地球物理流体分析中的应用潜力。图6展示了L2范数下的温度场真实值和预测值之平方误差。可以观察到，在最后的时间步，预测误差增加，这可能是由于模态系数预测不准确，以及POD基函数无法在外推时间域(即时间步超过1 500)捕获高精度的空间模式。针对LSTM误差累积的一种补救方法是以非自回归的方式来训练和部署网络[37]。

图5 平均温度场热力图(摄氏度)(地图资料来源于开源工具包 echarts-countries-pypkg)Fig.5 Heat map of sample averaged temperature field in degrees Celsius (The geographic map cities from the open source package echartscountries-pypkg)

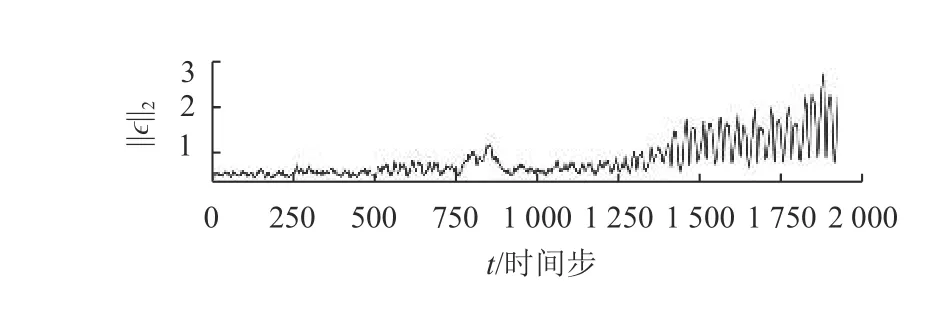
图6 真实温度场和预测温度场之差的L2范数随时间的变化Fig.6 Temporal variation of the L2-norm of the difference between the true and predicted temperature field

4 结论

本文提出了一种用于长短记忆神经网络结构自动搜索和超参数优化的遗传算法，可用于地球物理流体代理模型的建模任务。并且成功地证明了利用优化后的LSTM建立的代理模型能够预测海表温度场。为了便于更深层次神经网络的训练，本文采用了一种编码策略，其中LSTM网络使用了包含残差连接的更小的构件来设计。优化后的LSTM网络可以在足够长的时间内准确地预测海温场的季节变化，而不存在任何不稳定问题。

本文还观察到，真实模态系数和预测模态系数之间的差值在预测期间比训练期间的更大。这个问题可以通过使用非自回归部署或迁移学习的方法来解决，其中，LSTM网络在新数据可用时将被重新训练。在目前的研究中，本文假设每个隐藏层中的LSTM单元数目是恒定的。在未来的研究工作中，本文将消除这一约束，并对种群中的每个个体使用变长编码策略来优化LSTM网络。