回龙抽水蓄能电站库盆渗漏特性研究

谢遵党 吕小龙 宋修昌 马峰

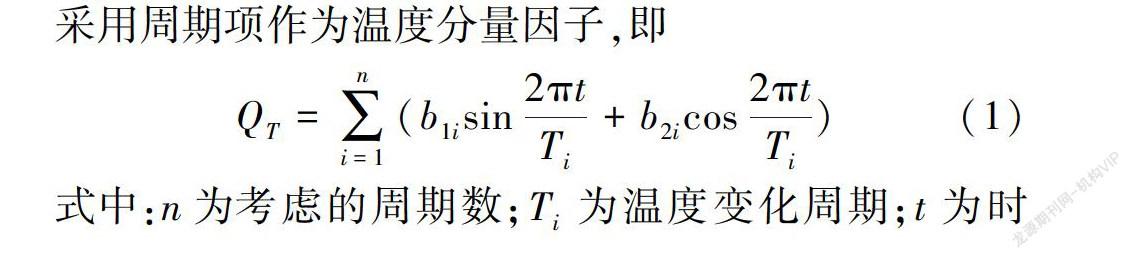
摘 要：抽水蓄能电站水位升降频繁、外部环境多变，长期运行过程中库盆渗控体系的老化问题十分突出。渗漏量是评价抽水蓄能电站库盆运行状態的关键监测指标，将库盆渗漏通道划分为堰型缺陷和深孔型缺陷，确定了水压、温度、时效分量影响因子。通过系统研究库水位、温度、时间对渗漏量的影响，建立了抽水蓄能电站库盆渗漏量统计模型。基于回龙抽水蓄能电站上水库库盆渗漏监测数据，验证了模型的准确性，为回龙电站库盆防渗治理提供了理论依据。

关键词：库盆渗漏;堰型缺陷;深孔型缺陷;统计模型;回龙抽水蓄能电站

中图分类号：TV641

文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.11.025

引用格式：谢遵党，吕小龙，宋修昌，等.回龙抽水蓄能电站库盆渗漏特性研究[J].人民黄河，2021，43（11）：133-136.

Study on Reservoir Basin Leakage of Huilong Pumped Storage Power Station

XIE Zundang  LYU Xiaolong  SONG Xiuchang  MA Feng3

（1.Yellow River Engineering Consulting Co.， Ltd.， Zhengzhou 45000  China; 2.Key Laboratory of Water Management

and Water Security for Yellow River Basin， Ministry of Water Resources （Preparation）， Zhengzhou 45000  China;

3.Huilong Branch of State Grid Xinyuan Co.， Ltd.， Nanyang 473002， China）

Abstract： Due to the frequent rise and fall of water level and the changeable external environment， the problem of reservoir basin leakage is prominent for pumped storage power station in the process of long-term operation. Leakage is a key index to evaluate the operation state of pumped storage power station basin. In this paper， the leakage channel of the reservoir basin was divided into weir-type defects and hole-type defects， the influence factors of water pressure component were determined. By systematically study the influence of reservoir water level， temperature and time on the leakage， a statistical model of reservoir basin leakage of pumped storage power station was established. Based on the leakage monitoring data of the upper reservoir basin of Nanyang Huilong pumped storage power station， the accuracy of the model was verified. At last， the time when the leakage of Huilong Reservoir basin exceeded the design limit （2，000 m3/d） was predicted， which provided a theoretical basis for the anti-seepage treatment of Huilong Reservoir basin.

Key words： reservoir basin leakage; weir-type weir type defect; hole-type defect; statistical model; Huilong Pumped Storage Power Station

随着经济社会的发展，我国用电结构和电网负荷特性发生了显著变化，电网峰谷差不断拉大和调峰容量不足的矛盾日益突出。抽水蓄能电站在电力系统中可以发挥调峰填谷、调频调相、提高供电质量等作用。目前，我国完工、在建、待建的抽水蓄能电站超过百座，早期建设的抽水蓄能电站经过长期运行，大多存在渗控体系老化问题[1-2]。抽水蓄能电站多为循环用水，水量的渗漏损失将严重影响工程的安全运行和电站经济效益的发挥。

基于工程监测资料建立数学模型，可实现对工程效应量的量化分析和预测，对保证工程安全运行具有重要意义。近年来，国内外学者在水利工程的结构健康监测领域取得了大量成果。王彭煦等[3]建立了指数型坝体沉降预报模型，与实测数据拟合良好。王颖慧等[4]将主成分分析法引入支持向量机中，同时应用灰狼优化算法对支持向量机进行参数优化，建立了PCA-GWO-SVM大坝变形预测模型。房彬等[5]构建了蓄水期坝顶水平位移的多元线性回归模型和串联灰色多元线性回归模型，分析预测了某拱坝蓄水期变形性态。秦鹏等[6]建立了ARIMA-RTA组合预测模型，该模型能够充分挖掘监测数据的动态信息，具有物理机制明确、预测精度高的优点。孙小冉等[7]将粗集理论和支持向量机结合起来，建立了大坝工作性态的RS-SVM实时监控模型，可实现外界环境荷载变化对大坝工作性态影响的监控和预测。刘亮亮等[8]将分形插值理论引入大坝变形预测，对某混凝土坝段的变形数据进行拟合，指出分形插值方法能较好拟合变形曲线，表征大坝变形特征。

上述成果主要针对大坝变形、坝体渗流等方面，而关于抽水蓄能电站库盆渗漏的研究成果很少。渗漏量是评价抽水蓄能电站库盆运行状态的关键监测指标。笔者通过系统研究库水位、温度、时间对渗漏量的影响，建立了抽水蓄能电站库盆渗漏统计模型，基于回龙抽水蓄能电站上水库库盆渗漏监测数据，预测了库盆未来渗漏趋势。

1 工程概况

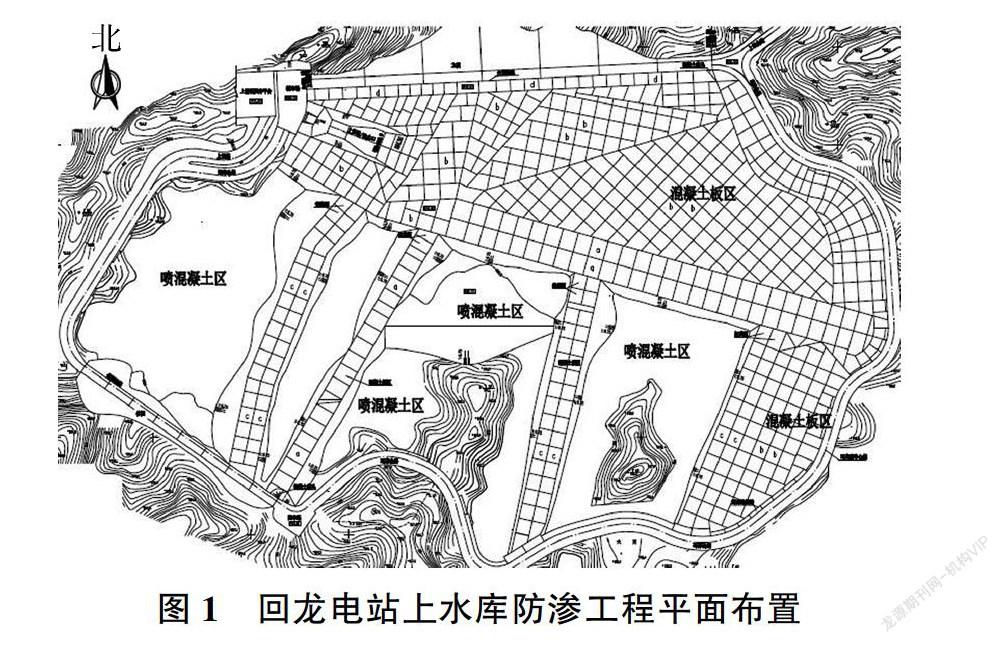
回龙抽水蓄能电站位于河南省南召县城东北约16 km的岳庄村附近，是为解决河南电力调峰问题而设置的调峰电站。工程主要建筑物包括上水库、下水库、引水发电洞、地下厂房、地面开关站等。上水库库盆防渗采用混凝土面板与挂网喷混凝土面层结合的全封闭防渗方案。在混凝土面板下设置无砂混凝土排水管网，喷混凝土区为15 m间隔的排水网格，通过穿坝钢管将库盆渗水排到坝后泵房集水池，再重新抽回库内。喷混凝土渗漏处理面积约5.46万m2，面板防渗处理面积约1.4万m2。

上水库库盆工程自2003年5月25日开始施工，2004年5月18日竣工。2004年6月上水库库盆开始蓄水，蓄水过程中，库盆渗漏量超过设计允许值。2005年，对库盆的喷混凝土区和部分混凝土面板区熔抹PVC改性沥青进行防渗处理，处理后满库渗漏量为917 m3/d。回龙电站上水库防渗工程平面布置见图1。

2 抽水蓄能电站库盆渗漏统计模型

抽水蓄能电站库盆渗漏量主要受库水位、时间效应、温度等因素的影响。渗漏量水压分量由库水位控制，随电站运行波动变化;时效分量指工程的渗透性和渗流条件等随时间的变化导致的渗漏量;温度分量是温度变化引起裂缝（缺陷）开合、材料胀缩等引起的渗漏量。综上，抽水蓄能电站库盆渗漏统计模型为

Q=QH+QT+Qt

式中：Q为库盆渗漏量;QH为水压分量;QT为温度分量;Qt为时效分量。

2.1 水压分量QH

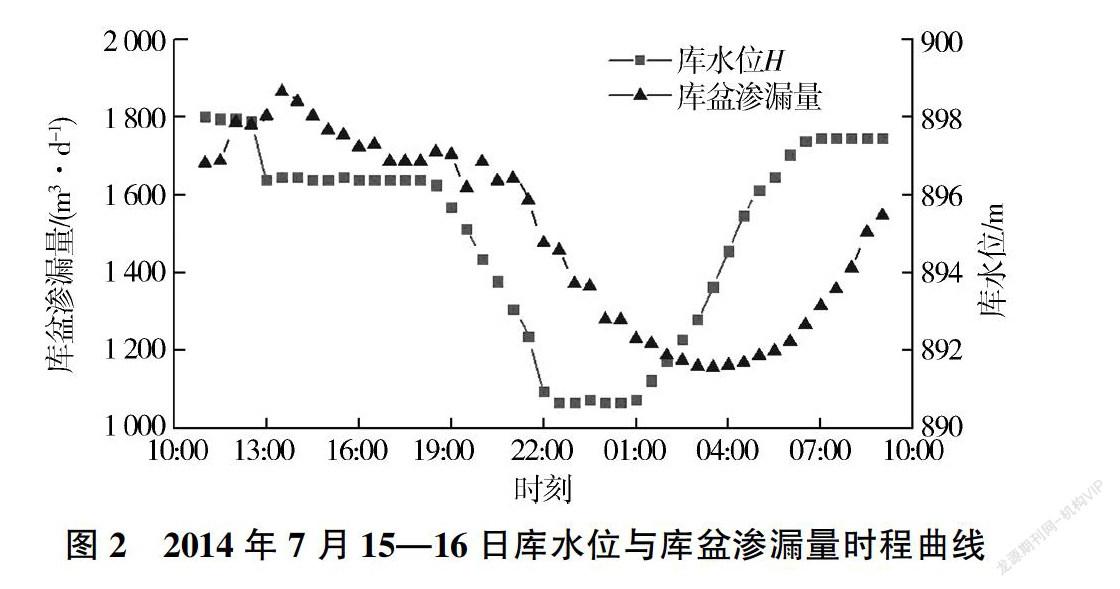
图2是回龙电站2014年7月15—16日库水位与库盆渗漏量时程曲线，可见库盆渗漏量Q与库水位H之间存在明显关联性。同时，库盆渗漏量变化与库水位升降之间存在一定滞后，系列数据表明，库水位下降导致库盆渗漏量减少的滞后时间约2.5 h，库水位上升导致库盆渗漏量增大的滞后时间约5.5 h。该滞后变化的主要原因是渗漏水在排水系统中汇集至坝后排水沟需要一定时间。

现场巡查表明，在水位变动区，防渗层裂隙与大气连通，水力条件与堰流类似。在水位变动区以下，裂隙与闸孔出流的水力条件基本一致。因此，将水位变动区以上裂缝定义为堰型缺陷，水位变动区以下定义为深孔型缺陷。根据《水力学计算手册》[9]，堰型缺陷Q∝H3/2，深孔型缺陷Q∝H1/2。考慮混凝土面板区和喷混凝土区的稳定渗流符合达西定律，因此稳定渗漏量Q∝H。综上，初步选择H1/2、H、H3/2等3个水压分量因子。

2.2 温度分量QT

图3是2014年7月15日库水位与库盆渗漏量滞回曲线，现场监测次序为O→A→B→C→D。A点和D点库水位基本一致，库盆渗漏量分别为1 070 m3/d和1 760 m3/d，这两点的渗漏量是昼夜温差引起的。

库盆防渗采用熔抹PVC改性沥青措施，随温度变化，热胀冷缩使裂缝宽度呈规律性张开或闭合。因此，采用周期项作为温度分量因子，即

QT=∑ni=1（b1isin2πtTi+b2icos2πtTi）（1）

式中：n为考虑的周期数;Ti为温度变化周期;t为时间;b1i和b2i为回归系数。

根据中国天气网数据，工程所在地日平均气温、日均最高气温和日均最低气温均呈周期性变化，因此选取周期为365 d。尽管库盆渗漏量在一天之内也呈周期性变化，但是考虑到库盆渗漏量的监测频率约为3 d，在长系列渗漏量预测中引入周期为1 d意义不大，因此分别选择sin2πt/365和cos2πt/365作为温度效应因子。

2.3 时效分量Qt

防渗体系随时间的演化规律较为复杂，根据相关研究成果[10]，在构造时效分量Qt时，初步选择5个时效因子，即t-0.5、t0.5、t、t2、lnt+1。

3 库盆渗漏统计模型验证及预测

3.1 影响因子组合方案

相关系数是一种衡量变量间相关程度的指标，其定义为

r（X，Y）=Cov（X，Y）Var[X]Var[Y]（2）

式中：Cov（X，Y）为向量X与Y的协方差;Var[X]为向量X的方差;Var[Y]为向量Y的方差。

为了确定影响因子组合方案，进一步筛选与库盆渗漏量相关性较高的影响因子，计算了库盆渗漏量与各影响因子的相关系数，见表1。库盆渗漏量Q与3个水压分量相关系数较大，同时水压分量之间相关性较强。库盆渗漏量与2个温度因子的相关系数差异性较大，与余弦因子相关系数较大，与正弦因子相关系数较小，正弦因子与余弦因子之间无相关关系。库盆渗漏量与时间因子t0.5、t相关系数极小，基本不存在相关关系，Q与t2、ln（t+1）为弱相关。综合考虑以上相关性分析成果，采用H1/2、H、H3/2、sin（2πt/365）、cos（2πt/365）、t2、ln（t+1）等7个影响因子作为组合方案构造数学模型。

3.2 库盆渗漏统计模型与趋势预测

采用回归方法对2012年1月5日—2014年12月31日的长系列监测数据进行拟合，确定库盆渗漏统计模型表达式：

Q=2.70×105h1/2-1.82×104h+308.09h3/2+5.54×10-4t2-

174.04ln（t+1）-30.00sin 2πt365+384cos 2πt365

采用库盆渗漏统计模型计算2012年1月5日—2014年12月31日逐日渗漏量，与监测数据比较见图4。可见，统计模型与监测数据整体趋势一致，各极值点差别不大，该模型较好地模拟了库盆渗漏量随时间的发展过程。

4 结 论

（1）熔抹PVC改性沥青进行防渗处理的库盆渗漏量对温度变化非常敏感，冬季库盆渗漏量显著大于夏季的。渗漏量变化相对库水位升降有一定滞后性，滞后程度与集水路径直接相关。

（2）通过分析库盆渗漏量影响因子及其相关性，建立了抽水蓄能电站库盆渗漏量统计模型，监测数据与模型预测计算结果基本一致，表明该模型具有较高的拟合精度。该模型可普遍适用于其他熔抹PVC改性沥青处理的混凝土防渗结构。

参考文献：

[1] 张春生，姜忠见.抽水蓄能电站设计[M].北京：中国电力出版社，2012：1-32.

[2] 汪顺生.抽水蓄能技术发展与应用研究[M].北京：科学出版社，2016：8-21.

[3] 王彭煦，宋文晶.水布垭面板坝实测沉降分析与土石坝沉降统计预报模型[J].水力发电学报，2009，28（4）：81-86.

[4] 王颖慧，苏怀智.基于PCA-GWO-SVM的大坝变形预测[J].人民黄河，2020，42（11）：130-134.

[5] 房彬，苏怀智，蔡德文，等.基于串联灰色多元回归模型的大坝蓄水期变形性态分析[J].水电能源科学，201 31（8）：106-108.

[6] 秦鹏，苏怀智，沈跃军.基于ARIMA-RTA组合模型的海堤工程沉降预测[J].水利水运工程学报，2013（5）：66-70.

[7] 孙小冉，苏怀智，彭建和.RS-SVM模型在大坝安全监控中的应用[J].人民黄河，2016，38（7）：130-133.

[8] 刘亮亮，陈旭东.基于分形插值的混凝土坝变形趋势分析[J].人民黄河，2020，42（8）：146-149.

[9] 李炜.水力学计算手册[M].北京：中国水利水电出版社，2005：73-76.

[10] 张秀丽，杨泽艳.水工设计手册[M].北京：中国水利水电出版社，2014：387-454.

【责任编辑 张华岩】