基于巴基斯坦阿扎德帕坦大桥抗震设计的中美规范对比研究
2021-12-08王伦文何俊荣赵胤儒
王伦文 何俊荣 赵胤儒
摘要:为对比研究美国AASHTO桥梁抗震规范与中国公路桥梁抗震规范的差异,基于巴基斯坦阿扎德帕坦(Azad Pattan)大桥的抗震设计,采用通用有限元软件Midas Civil进行了抗震计算。结合计算结果分析了两国规范在桥梁抗震设计理念、地震动参数、抗震计算方法、抗震构造设计等方面的异同,总结了美国规范中关于桥梁抗震设计的经验。分析结果可为海外桥梁工程的抗震设计借鉴。
关键词:桥梁工程;抗震设计;AASHTO规范;有限元分析;阿扎德帕坦大桥;卡洛特水电站;巴基斯坦
中图法分类号:U442.55文献标志码:ADOI:10.15974/j.cnki.slsdkb.2021.11.014
文章编号:1006 - 0081(2021)11 - 0061 - 05
0 引 言
随着桥梁工程的不断发展,桥梁抗震理论正在逐步完善,但世界各国的桥梁抗震规范体系存在较大差异[1]。随着“一带一路”倡议的推进,大量海外工程项目将直接涉及国外规范,对于工程师来说,熟悉和掌握国外相关规范至关重要。
根据合同要求,巴基斯坦卡洛特水电站的库区复建桥梁——阿扎德帕坦(Azad Pattan)大桥须参照当地规范及美国规范进行设计。卡洛特水电站工程场址区50 a超越概率10%的地震动峰值加速度为0.26 g,地震基本烈度为Ⅷ度,属于高烈度地区,抗震设计对于阿扎德帕坦大桥来说尤为重要。
本文结合阿扎德帕坦大桥的抗震设计,针对美国[2]《AASHTO LRFD Bridge Design Specifications》(以下简称“AASHTO规范”)和中国《公路桥梁抗震设计规范》[3](以下简称“中国规范”)进行对比研究,总结了美国规范中关于桥梁抗震设计的经验。
1 工程概述
1.1 工程简介
阿扎德帕坦大桥为卡洛特水电站库区复建桥梁,距大坝坝址约26 km,桥型设计为三跨预应力混凝土变截面连续刚构,跨径组成为(50+90+50)m。箱梁横断面采用单箱单室,根部梁高6.0 m,跨中梁高3.0 m,中间梁段采用1.6次抛物线过渡。下部结构1号和2号桥墩采用带圆端的矩形实体墩,0号和3号桥台采用重力式桥台,桥墩桥台均配置桩基承台。结构所用材料的性能标准均按照美国规范执行。
1.2 场地分析
工程场地在区域大地构造单元上位于喜马拉雅西构造结南部的哈扎拉-克什米尔共轴褶皱体内,强震构造主要为喜马拉雅主边界冲断带(MBT)和主前缘断裂带(MFT),距离场址最近的发震构造为穆扎法拉巴德(Muzaffarabad)断裂,于2005年发生克什米尔里氏7.6级地震。在新构造运动时期,处于主边界断裂和主前缘断裂之间的近场区以整体间歇性抬升活动为主,内部差异性活动较弱,属构造相对稳定地区。
1.3 结构分析
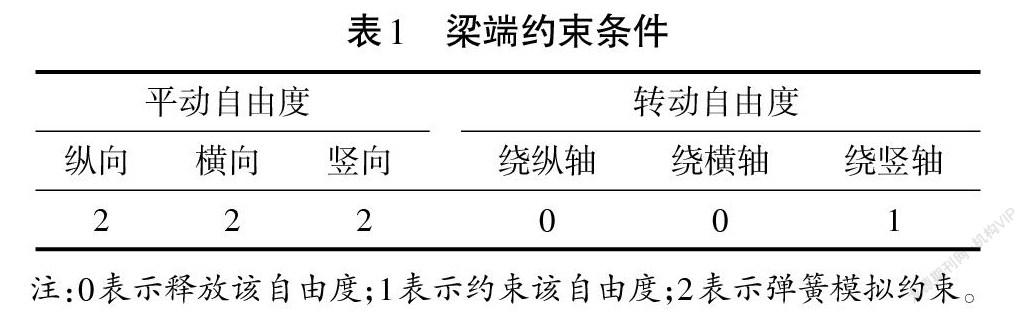
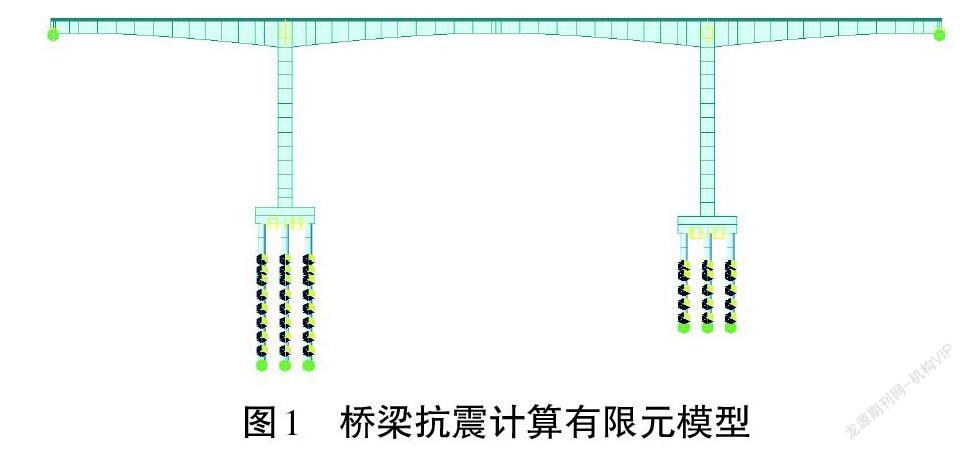
阿扎德帕坦大桥结构对称,刚度均匀分布,属于规则桥梁,根据规范要求,可采用反应谱分析法计算。全桥抗震受力分析采用大型通用有限元软件Midas Civil进行计算,考虑桩-土相互作用,桩基础土弹簧刚度采用m法进行计算模拟。桥墩及主梁混凝土容重均按ASTM标准取值,桥面铺装以附加质量的形式作用在结构上,边跨梁端约束条件见表1。桥梁抗震计算有限元模型如图1所示。
2 基于美国AASHTO规范的抗震设计
2.1 地震动参数
根据地震安评报告和AASHTO规范,桥址处75 a超越概率7%的地震动峰值加速度为0.30 g。结构阻尼比取值为0.05,地震动加速度反应谱[2]如图2所示,0~0.2 Ts段为上升段,0.2 Ts~Ts段为平直段,Ts~1.0 s段为下降段。
2.2 抗震分析
根据AASHTO规范[2],分别输入水平地震作用按相互垂直的纵桥向和横桥向。由于地震作用的方向具有随机性,两个正交方向的地震力具有同时发生的可能性,先分别计算两个方向的地震作用,再进行两个方向的不同组合:①组合1为1.0倍纵向地震效应与0.3倍横向地震效应之和;②组合2為0.3倍纵向地震效应与1.0横向地震效应之和。
2.3 抗震计算结果
由Midas Civil软件计算得到的地震工况下桥梁下部结构内力结果及配筋如表2所示,关键节点的位移如表3所示。
2.4 抗震构造要求
在AASHTO规范中,根据桥梁结构抗震风险等划分了抗震设计类别。墩柱的设计类别不同,其纵向钢筋最小配筋率也存在差异。AASHTO规范[2]中规定:B类和C类墩柱的最小纵向钢筋配筋率为0.7%;D类墩柱的最小纵向钢筋配筋率为1.0%。规范中还对纵向钢筋的最大直径、最小锚固长度做了相关规定。延性构件的最大纵向钢筋配筋率为4%。
AASHTO规范中要求墩柱箍筋最小体积配箍率不小于0.4%,箍筋最小直径为12.7 mm。
3 基于中国规范的抗震设计
3.1 地震动参数
根据地震安评报告,桥址处50 a超越概率10%的地震动峰值加速度应取0.26 g,设防烈度为Ⅷ度。结构阻尼比取值为0.05,地震动加速度反应谱如图3所示[1],0~0.1 s段为上升段,0.1s~Tg段为平直段,Tg~10 s段为下降段。对应的反应谱函数为
[S=Smax(0.6T/T0+0.4) T≤T0Smax T0≤T≤TgSmax(Tg/T) Tg≤T≤10]
3.2 抗震分析
根据规范要求[3],抗震设防烈度为Ⅷ度和Ⅸ度的大跨度结构应同时考虑顺桥向X、横桥向Y和竖向Z的地震作用。采用反应谱法或功率谱法,同时考虑3个正交方向(纵向X、横向Y和竖向Z)的地震作用时,可分别计算3个正交方向的地震作用效應最大值Ex、Ey、Ez,然后进行平方和开方求得总的最大地震作用效应E,具体计算公式如下:
[E=Ex2+Ey2+Ez22]
3.3 抗震计算结果
由Midas Civil软件计算得到的E2(大震)地震工况下桥梁下部结构内力结果如表4所示,关键节点位移计算结果如表5所示。
3.4 抗震构造要求
对于抗震设防烈度Ⅶ度及Ⅶ度以上地区[3],墩柱潜在塑性铰区域内加密箍筋的配置要求如下:①箍筋加密区长度应不小于墩柱弯曲方向1.0倍截面宽度或墩柱弯矩超过最大弯矩80%的范围;②对于短柱(墩柱高度与截面高度之比小于2.5)应采取全高加密;③加密箍筋最大间距不应超过10 cm,且不大于6倍纵向钢筋直径;④箍筋直径不应小于10 mm;⑤墩柱加密区域箍筋应延续到盖梁和承台内,延伸范围不应小于墩柱长边尺寸的1/2,且不小于50 cm。
墩柱的纵向钢筋宜对称配筋,纵向钢筋最小配筋率不宜小于0.6%,不应超过4%。
4 两国规范对比分析
通过对比阿扎德帕坦大桥的抗震设计,可以发现中美两国的规范存在较大差异。下面将从桥梁抗震设计理念、地震动参数、抗震计算方法、抗震构造设计等方面进行差异分析。
4.1 抗震设计理念
桥梁结构抗震设计理念可以概括为基本设计思想和设计准则,是抗震设计的核心部分,决定了抗震设计所要达到的性能目标、采用的设计地震动参数和地震作用计算方法。当前主流的桥梁抗震设计方法有两种:①基于强度;②基于位移。AASHTO规范和中国公路规范均采用基于位移的抗震设计方法,中国的铁路桥梁抗震规范则采用基于强度的抗震设计方法[4]。
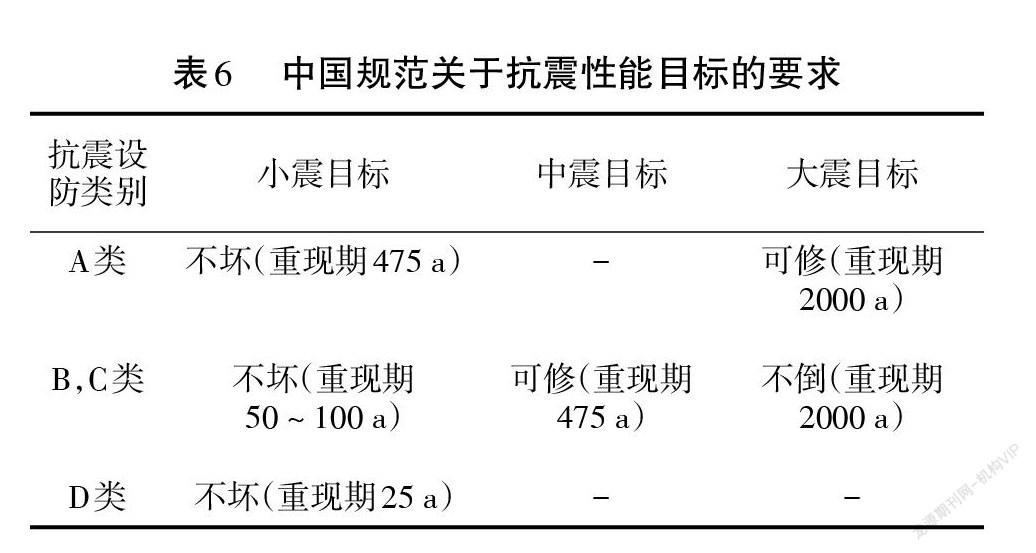
桥梁结构抗震设计中,首先需要确定设防标准,综合考虑社会经济条件来确定合理的设防参数[3]。根据公路桥梁的重要性和在抗震救灾中的作用,中国规范中将公路桥梁分为A,B,C,D这4个抗震设防类别,并以此确定不同的设防标准和设防目标。中国规范的抗震性能目标为“小震不坏、中震可修、大震不倒”,具体要求见表6。以B、C类桥梁为例,其抗震设计仅进行多遇地震下的弹性抗震设计和罕遇地震下的延性抗震设计,满足了这两个阶段的性能目标要求后,即认为已满足设防地震可修的目标。因此,中国规范本质上采用的是两水准设防和两阶段设计。
针对规则的桥梁结构,AASHTO规范中通常采用重现期为1 000 a(即75 a超越概率7%)的地震动峰值加速度进行抗震设计,要求桥梁结构在地震发生后几乎不会倒塌。同时,业主有权利根据桥梁的重要性提高性能目标要求。
AASHTO规范与中国规范的最低抗震性能目标相同,均为桥梁不倒塌[5]。差异在于:中国规范中采取的是两水准设防和两阶段设计;AASHTO规范中对于桥梁的最低性能标准要求仅适用于规则桥梁,即规则桥梁采用一阶段设计,而对于不规则桥梁,业主有权根据实际情况提出更高的性能目标要求。
4.2 地震动参数
AASHTO规范和中国规范对于混凝土结构的阻尼比取值均为0.05,并要求考虑阻尼比修正系数,当阻尼比不等于0.05时,AASHTO规范中采用表格插值计算阻尼比修正系数,中国规范中采用公式[Cd=1+0.05-ξ0.06+1.6 ξ≥0.55]对阻尼比修正系数进行计算。总体来说,阻尼比参数的差异较小。
基于设防水准的不同,两国规范对于地震作用的重现期规定存在较大差异,AASHTO规范中,针对规则桥梁,采用重现期为1 000 a(即75 a超越概率7%)的地震动峰值加速度,中国规范针对B,C类桥梁小震作用重现期为50~100 a,中震作用重现期为475 a,大震作用重现期为2 000 a。可以发现,AASHTO规范设计水准下的地震作用重现期高于中国规范的设防地震作用(中震)重现期。
对于反应谱曲线的规定,主要区别在于两国规范对于反应谱峰值加速度对应的自振周期起点不一致。中国规范中加速度反应谱最大适用周期为10 s,AASHTO规范中加速度反应谱的最大适用周期仅1 s,故中国规范的适用范围更广。
两国规范中对场地类别的划分也存在差异。根据土层平均剪切波速和场地覆盖土层厚度,AASHTO规范将场地划分为A~F共6类场地,中国规范将场地划分为Ⅰ~Ⅳ共4类,其中Ⅰ类分为Ⅰ0和Ⅰ1类。
4.3 计算方法
AASHTO规范与中国规范中均采用基于位移的抗震设计方法[6],就是将结构的性能目标作为控制结构抗震设计的依据。但不同之处在于:中国规范采用的是两阶段设计,即桥梁在E1地震作用下进行弹性抗震设计,在E2地震作用下进行延性抗震设计,并引入能力保护设计原则;AASHTO规范采用的是一阶段设计,即在设防地震作用下验算结构的强度和位移。
根据AASHTO规范,水平地震作用按相互垂直的纵桥向和横桥向分别输入。由于地震作用的方向具有随机性,两个正交方向的地震力具有同时发生的可能性,先分别计算两个方向的地震作用再进行两个方向的不同组合:①组合1为1.0倍纵向地震效应与0.3倍横向地震效应之和;②组合2为0.3倍纵向地震效应与1.0横向地震效应之和。上述地震作用与恒载及活载作用效应进行组合时,共同构成极端事件极限状态I的荷载组合,用于桥梁一阶段设计的强度验算。而中国规范中规定,抗震设防烈度为Ⅷ度和Ⅸ度大跨度结构应同时考虑顺桥向、横桥向和竖向的地震作用。采用反应谱法或功率谱法计算3个正交方向的地震同时作用时,可采用单个方向的地震作用产生的最大效应进行组合,然后进行多遇地震作用下的结构强度验算。可以发现,中国规范中要求考虑竖向地震作用对于高烈度区大跨度结构的影响。因此,在结构地震作用组合及其效应方面,两国规范存在较大差异。
基于位移的抗震设计方法本质是延性抗震设计,其核心问题在于桥梁结构的位移需求与位移能力的确定[5]。中国规范与AASHTO规范中关于位移需求与位移能力的验算指标尚存在差异。中国规范中根据桥梁结构的规则程度不同,制定了不同的验算指标,主要包括:①非规则桥梁在罕遇地震作用时,采用塑性铰区域的转角作為验算指标;②规则桥梁采用罕遇地震作用下的桥墩墩顶位移作为验算指标。而AASHTO规范中则将桥梁上部结构质心处的位移作为验算指标,且不同抗震设计类别的桥梁结构具有不同的位移验算标准。
对比阿扎德帕坦大桥的计算结果可以发现,采用AASHTO规范需要配置更多的桥墩或者桩基钢筋。这是由于AASHTO规范在进行强度验算时采用更高重现期的设防水准,导致反应谱曲线的峰值加速度更大。中国规范进行延性抗震设计时,采用的弯矩-曲率来判别截面是否处于弹性状态。同时基础作为能力保护构件设计时,AASHTO规范中要求考虑墩柱的弯矩超强系数,中国规范中规定结构未进入塑性状态时,可直接采用罕遇地震作用下的地震组合内力值。
4.4 抗震构造设计
由于两国规范采用类似的设计方法,因而在抗震构造设计方面的要求总体类似,如延性构件的最大纵向配筋率均为4%,最小体积配箍率约为0.4%,潜在塑性铰区的长度要求等。主要区别有:中国规范要求的延性构件最小纵筋配筋略小于AASHTO规范,未对纵向钢筋的最大直径和最小直径进行规定;中国规范要求加密区最小箍筋直径为10 mm,AASHTO规范要求为12.7 mm。
5 结论与建议
本文结合巴基斯坦阿扎德帕坦大桥项目,分别利用美国AASHTO规范和中国规范进行抗震设计,针对两者的抗震输入和输出数据从抗震设计理念、地震动参数、抗震计算方法和构造设计共4个方面进行比较分析,得出如下结论,并提出可行性建议。
(1)关于抗震设计理念方面,AASHTO规范和中国规范中均采用基于位移的设计方法,具有相同的最低抗震性能目标,区别在于中国规范中采用两水准设防和两阶段设计,AASHTO规范中采用一阶段设计,而对于不规则桥梁,中国规范中有明确要求,AASHTO规范中较为模糊,将决策权交由业主。海外项目抗震设计时,不规则桥梁建议根据业主的要求进行抗震设计,同时不低于中国规范中要求的最低抗震性能目标。
(2)关于地震动参数方面,显著区别在于AASHTO规范中要求设防地震作用的重现期为1 000 a,中国规范中要求设防地震作用的重现期为475 a。另外关于加速度反应谱曲线和场地类别划分亦存在微小差异。海外项目抗震设计时,建议以AASHTO规范中要求的重现期1 000 a的地震作用进行抗震设计,以中国规范中要求的重现期2 000 a的罕遇地震作为延性设计的校核地震。
(3)关于抗震计算方法方面,两者总体设计思路相同,具体操作存在一些差异:中国规范中规定多遇地震作用下为弹性抗震设计,罕遇地震作用下进行延性抗震设计,并引入能力保护设计原则;AASHTO规范中采用一阶段设计,验算设防地震作用下的结构强度和位移,且在能力保护构件设计的内力取值方面存在差异。通常情况下,AASHTO规范中得到的截面配筋率高于中国规范。海外项目抗震设计时,有如下建议:设防烈度为Ⅷ度和Ⅸ度的大跨度结构应同时考虑顺桥向、横桥向和竖向的地震作用组合;基础作为能力保护构件,其上部墩柱弯矩超强系数建议以AASHTO规范中要求的1.3取值,确保塑性铰位置不发生转移。
(4)关于抗震构造设计方面,两者对于延性构件的纵向钢筋配筋率、加密区箍筋体积配筋率和塑性铰长度等方面的规定较为相似,但AASHTO规范相比中国规范略为严格。海外项目抗震设计时,建议提高延性构件最小纵筋配筋率和箍筋直径,最小纵筋配筋率按0.7%控制,最小箍筋直径按12 mm控制。
参考文献:
[1] 熊韬.中美桥梁抗震规范对比研究[J].工程建设与设计,2016(3):80-81.
[2] LREDSEIS-2 AASHTO LRFD Bridge Design Specifications[S].
[3] JTG/T 2231-01-2020 公路桥梁抗震设计规范[S].
[4] 冯国军.中美铁路桥梁抗震设计对比研究[J].铁道标准设计,2013(5):68-71.
[5] 刘婧. 基于中美规范设计的连续刚构桥地震易损性研究[D]. 湖南:长沙理工大学,2015.
[6] 殷鹏程,叶爱君.从中美规范比较探讨桥梁结构抗震体系[J].工程抗震与加固改造,2009,31(3):1-8,15.
(编辑:唐湘茜)
A comparative study of Chinese and American seismic design codes based on Azad Pattan Bridge in Pakistan
WANG Lunwen,HE Junrong, ZHAO Yinru
(Changjiang Survey, Planning, Design and Research Co., Ltd., Wuhan 430010, China)
Abstract:In order to compare and study the differences between American AASHTO bridge seismic code and Chinese highway bridge seismic code, based on the seismic design of Azad Pattan Bridge in Pakistan, the general finite element software MIDAS civil is used for seismic calculation. According to the calculation results, the similarities and differences of seismic design concept, ground motion parameters, calculation method and anti-seismic structure design between the two codes are analyzed. Finally, the experience of the U.S. code on the seismic design of bridges is summarized to provide reference for the seismic design of overseas bridge projects.
Key words:bridge engineering; seismic design; AASHTO standard; finite element analysis; Azad Pattan Bridge; Karot Hydropower Station; Pakistan
