风光互补发电系统的建模与仿真研究

王汀元

【摘  要】论文基于一种较为先进的风-光-储混合发电的模型，通过分析风能发电和光伏发电的特性，分别搭建风力发电、光伏发电的数学模型，再基于数学模型，利用MATLAB/Simulink实验平台搭建仿真模型，运行得到结果后对其进行简要分析。论文总结风力发电和光伏发电的优势与劣势，并制定能够使其互补的控制策略，实现减少“弃风、弃光”现象的目的。

【Abstract】This paper is based on a more advanced wind-photovoltaic-storage hybrid power generation model. By analyzing the characteristics of wind power generation and photovoltaic power generation， the paper constructs mathematical models of wind power generation and photovoltaic power generation respectively. Then， based on the mathematical models， the paper uses the MATLAB/Simulink experimental platform to construct a simulation model， and briefly analyzes the results after running. The paper summarizes the advantages and disadvantages of wind power generation and photovoltaic power generation， and formulates a control strategies that can complement each other to achieve the goal of reducing the phenomenon of "abandoning wind and solar energy".

【关键词】风光互补发电;控制系统;混合储能;建模

【Keywords】wind-photovoltaic hybrid power generation; control system; hybrid energy storage; modeling

【中图分类号】TM61                                             【文献标志码】A                                                 【文章编号】1673-1069（2021）12-0179-03

1 风光发电系统模型的建立

1.1 风力发电机组模型与控制系统

根据贝茨定律，可以得到风机发电功率的数学模型：

式中，Cp为风能利用系数;ρ为空气密度，单位是kg/m3;R为风轮机的半径，单位是m;V为风速，单位是m/s。

通过式（1）可知，若在风轮机半径、风速以及空气密度为常数的情况下，风机从风能中获取的功率随着风能利用系数Cp的增加而成线性增加。

其中，风能利用系数Cp是关于叶尖速比λ和桨距角β的非线性函数。有如下关系式：

式中，ω为风力角速度，单位是rad/s;n为风机的转速，单位是r/min。Cp和λ存在如下关系：

由图1可知，当桨距角β一定时，Cp随着λ的变化而变化，且在λ的变化过程中，存在一点λm使得Cp最大，从而使得风机输出的机械功率最大。故而，λnom被称为最佳叶尖速比。

由上述可知，风机输出的机械转矩为：

通过对数学模型的分析可得，桨距角β值为0时，风能利用率最大;β值约为20时，风能利用系数最小。β值越大风能利用系数的值越小。通过物理模型，外界风速小于额定风速时，风机的桨距角β一直保持为0，因而，由图1可知，此时的风能利用系数Cp是叶尖速比λ的函数，通过对叶尖速比λ的实时调节，可以得到一个最大的风能利用系数Cpmax，从而使得输出功率最大。

将叶尖速比λ的表达式带入发电功率的公式中可以求出：

由以上可知，通过控制发电机的转速，使其一直工作在最佳叶尖速比曲線上，可以实现风力发电机最大功率追踪的目的，此种最大功率点追踪的方法称为叶尖速比控制法。

1.2 光伏发电机组模型与控制系统

在光照条件下的PN结可以等效为一个二极管和一个电流源的并联，依据这个原理可以将由光伏电池组成的系统等效为一个电路。其中，电路满足的约束关系如下：

I=IL-ID-ISH                 （5）

式中，I为光伏电池的工作电流;IL为光生电流;ID为PN结的结电流;在实际电路中，需要考虑光伏电池的内阻RSH，流过它的电流即ISH，故基本的工作电路可列以下表达式：

在上述公式中，I0为恒定值，其大小与二极管的性质有关;q为电子电荷;VD为二极管两端的等效电压;V为二极管两端的输出电压;T为光伏电池的工作温度;k为玻尔兹曼常数。

光伏电池的最大功率点追踪算法有许多，在工作时，大多采用改变直流侧工作电压来发挥调节输出功率的作用。常见的最大功率点追踪算法有：电压控制法、电导增量法、扰动观察法、模糊控制算法、神经网络控制算法。

本文采用电导增量法对光伏电池实行MPPT控制。

光伏输出特性曲线同样是一条连续的单峰曲线，如图2所示。

在峰值处有功率与电压的导数为0，即dP/dU=0，电导增量法则是根据这一点，寻找该曲线上导数为0的点，即为最佳工作点。当实际工作环境产生变化，实际工作点在最佳工作点附近来回移动，控制系统通过对工作点功率对电压的导数进行分析，可以实现对最大功率点的跟踪。

2 储能系统的充放电策略

2.1 基于天气情况的控制策略

控制策略可以是根据不同的天气情况下，光照、风力不同的条件下整个系统的输出发电量能否满足用电端对电量的需求的变化情况进行制定的策略。

以下是对控制原理的介绍：系统会检测对比系统的输出电能功率与用电端的电力需求，如果输出大于需求，那么多余电量会向储能系统输送，此时储能系统是充电状态。如果，输出小于需求，那么储能系统会辅助向用电端输送电能，此时储能系统处于放电状态。具体工作模式如表1所示。

上表中，首先是根据天气情况的风力和光照强度不同分成4种情况，其次根据系统产生的电能功率和用电端负载用电需求情况对比分成7种情况。

2.2 基于储能容量情况的控制策略

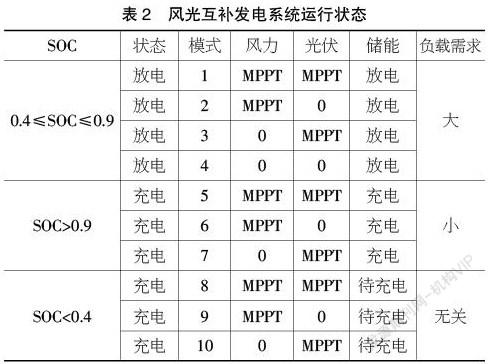
控制策略可以是为了提高资源利用率，并减少“弃风、弃光”的情况（即减少受限于某种原因被迫放弃风水光能，停止相应发电机组或减少其发电量的情况），而采取的一种基于储能容量情况的控制策略。其具体的操作逻辑是：通过监测储能系统中的蓄电池的SOC状态，从而决定风光互补系统发出的电能功率是全部提供给用户，还是部分给用户部分给储能系统等。通过此套策略可以较好地处理上一控制策略中的“弃风、弃光”难题，可以更好地节约能源，利用能源。其具体运行逻辑如表2所示。

下文对这几种模式进行分析。当运行状态处于模式1～4时，此时，储能系统处于持续放电状态，此时根据用电端不同的用电需求，对风光互补发电的电能直接向用户端输送和从储能系统中蓄电池向用户端输送电能等不同情况进行适时调整，此时系统状态是比较繁忙的，都是由储能系统向负载端进行电能输送，分别在有风有光、有风无光、无风无光几种情况下运行，但是当SOC达到相应下限时，剩余后期的不满足的部分向电网取电，此时储能系统的蓄电池又转变为充电状态。

当运行状态处于模式5～10时，此时系统运行均在储能系统的蓄电池的充电状态，此时只需考虑SOC状态。

其中，当运行状态在模式5～7时，此时为蓄电池充电状态。同理可在有风有光和有光无光等状态下运行，当SOC达到上限，此刻运行状态和上述模式1～4相同，蓄电池又转变为放电状态。

当运行状态在模式1～8时，完全处于自给自足的孤岛状态，处于一個守恒状态。

当运行状态在模式8～10时，虽然也是处于蓄电池充电状态，但是其平衡时系统输出电能功率与用电端需求相平衡。

3 风光互补发电系统的建模与仿真分析

将仿真时间设置为1s，温度设置为25℃，蓄电池初始电量设置为70%。为了使仿真过程更贴近实际，将整个仿真过程划分为3个阶段。光能在正常情况下，早上时逐渐增大，在中午升至最大，在下午逐渐减小;风能一天中的变化较为随机。所以，第一是有光无风阶段，第二是有光有风阶段，第三是无光有风阶段。分别对应在0.3s时，风速由4m/s变化为13m/s，光照强度由700W/m2变化为900W/m2;在0.6s时，风速由13m/s变化为16m/s，光照强度由900W/m2变化为300W/m2，运行模型。

分析仿真所得结果，风电和光电的负载消耗均维持在40kW左右，若风力发电和光伏发电的总功率大于二者的负载消耗总和时，风光互补发电系统为蓄电池充电;反之，蓄电池放电，为负载供电。通过蓄电池的荷电状态可以看出其工作状态。

在0～0.3s期间，系统模拟了有光无风的情况，此时光伏发电输出功率为50～60kW，大于光电负载消耗，光电蓄电池开始充电，荷电量增加;风力发电的输出功率较低，在1～2kW，远远无法满足风电负载，此时，风电蓄电池开始对外供电，荷电量减小。

在0.3～0.6s期间，系统模拟了有光有风的情况，风电输出功率在30kW左右，但是依然无法满足风电负载所需，所以蓄电池进一步对外供电，但是可以看出，SOC曲线的变化速度趋缓;光伏发电对外功率提升至70～80kW，光电蓄电池SOC上升趋势增大，充电速度加快。

在0.6～1s期间，系统模拟了无光有风的情况，风电输出进一步提升至50～60kW，已经可以满足负载消耗，故风电蓄电池开始充电，SOC曲线上升;光电输出下降至30kW以下，不足以提供负载足够的电能，光电蓄电池开始对外供电。

4 结语

本文将风光互补发电系统的仿真与实际天气状况进行了结合，研究了在不同天气条件下的发电情况和充放电控制策略，将互补系统先拆解为独立的发电系统进行数学模型的研究和仿真模型的建立，通过风电和光电各自的算法实现最大功率点的追踪。在通过简单测试确保模型可靠后，分别与各自的蓄电池模型连接，再结合起来对负载供电。最终增加模拟负载功率的模块，并制定了合适的控制策略，从而使发电系统在供电与充电模式之间切换，达到减少“弃风、弃光”的目的。

【参考文献】

【1】邢立强.风光互补发电系统混合储能的优化控制研究[D].乌鲁木齐：新疆大学，2020.

【2】刘高强.风光互补发电系统控制器的设计与控制[J].科技与创新，2020（18）：144-145.

【3】孟德越，刘伟，崔茂齐.风光互补发电系统协调控制策略与并网研究[J].河北水利电力学院学报，2021，31（2）：51-55+66.

【4】赵艳梅.风光互补发电的技术难点及发展趋势[J].中国高新科技，2020（13）：77-78.

【5】万永康，赵盛杰，宋鹏程，等.风光互补发电控制策略研究[J].决策探索（中），2020（9）：65-66.