中国人口平均预期寿命预测及其面临的问题研究
2021-12-08王广州


摘 要:以经典的LeeCarter死亡率模型为工具,采用中国1994—2019年死亡数据,构建LeeCarter死亡率模型,研究中国人口平均预期寿命预测问题。研究表明:虽然中国死亡数据资源越来越丰富,但不同来源数据质量差距和冲突依然比较明显。随着死亡水平的下降,1994年以来1‰人口变动抽样调查死亡数据面临的质量问题比较突出。从LeeCarter死亡率模型拟合效果来看,模型拟合年龄别死亡率平均相对误差较小的年龄组为40—84岁,0岁组拟合效果较差,而0岁人口死亡率的数据质量在模型拟合、平均预期寿命推算和预测过程中非常重要。由于年龄别死亡率数据误差相抵的原因,对出生人口平均预期寿命的推算误差明显下降。在平均预期寿命研究结果的应用过程中,对不同年龄人口平均预期寿命的相对误差和绝对误差需要区别对待。考虑到中国历史数据的质量问题,在建模过程中需要防止模型对基础数据的过度拟合问题。由于死亡人口重报,特别是多报的可能性很小,现有数据和模型对人口平均预期寿命的估计或预测肯定是一个高估。
关键词:LeeCarter模型;平均预期寿命;死亡率;数据质量
中图分类号:C921 文献标识码:A 文章编号:1000-4149(2021)06-0022-18
DOI:10.3969/j.issn.1000-4149.2021.00.046
Abstract: By means of the classical LeeCarter mortality model and Chinese mortality data from 1994 to 2019, this paper constructs the LeeCarter mortality model to study the prediction of Chinese life expectancy at birth. The research shows that although Chinese mortality data sources are get rich step by step, the gap and conflict of data quality from different sources are still obvious. With the decline of mortality level, the quality problem of mortality data in 1‰ population change sampling survey since 1994 is more prominent. From the fitting effect of Lee-Carter mortality model, the age group with small average relative error in fitting agespecific mortality is 40-84 years old, and the fitting effect of 0-yearold group is poor. The data quality of 0-yearold population mortality is very important in the process of model fitting, calculation and prediction of life expectancy at birth. Due to the error offset of agespecific mortality data, the estimation error of life expectancy at birth decreased significantly. In the application of the research results of life expectancy at birth, the relative error and absolute error of life expectancy at birth of population for different ages need to be treated differently. Considering the quality of Chinese historical data, it is necessary to prevent the model from over fitting in the modeling process. Since there is little possibility of rereporting, especially over reporting, the existing data and models must overestimate or over prediction the life expectancy at birth.
Keywords:LeeCarter model;life expectancy;mortality;data quality
一、研究背景
平均預期寿命不仅是人口科学研究的重要指标,同时也是很多相关科学研究关注的重要内容。平均预期寿命之所以重要,是因为一方面平均预期寿命是健康水平的重要测量指标,另一方面平均预期寿命也是社会发展和科技进步的标志。在人类社会进步的历史长河中,对寿命的关注远远超出许多其他事物。1662年从格兰特(Graunt)提出生命表开始[1],平均预期寿命的基本概念和测量体系逐步成为人口科学、社会保障、卫生健康等许多基础研究的重要分析工具。长期以来,平均预期寿命不仅是联合国开发计划署人类发展指数(HDI)构建的三大重要基础变量之一,同时也是中国国民经济和社会发展规划的重要指标。
2016年10月,中共中央、国务院印发了《“健康中国2030”规划纲要》。2017年10月,十九大报告中指出实施健康中国战略。2019年11月,中共中央、国务院印发了《国家积极应对人口老龄化中长期规划》,2020年10月,《中国共产党第十九届中央委员会第五次全体会议公报》提出实施积极应对人口老龄化国家战略。无论是健康中国战略还是积极应对人口老龄化国家战略都离不开对未来健康水平的监测评估,而平均预期寿命正是连接和判断两大国家战略进展情况的重要统计指标和分析工具。
除了国家重大发展战略外,随着社会经济的发展和数据采集能力的提高,国民经济和社会发展规划对平均预期寿命予以高度重视。早在“十二五”规划中,人均预期寿命出生人口平均预期寿命或平均预期寿命在各项规划中均简化为人均预期寿命。就被列为重要的规划目标。“十二五”期间人均预期寿命规划目标是到2015年人均预期寿命达到74.5岁,但2015年实际人均预期寿命为76.34岁数据来源:《中华人民共和国国民经济和社会发展第十三个五年规划纲要》,简称“十三五”规划纲要。,远远超过规划目标的要求。“十三五”规划人均预期寿命则列为预期性指标,并没有明确提出预期目标的具体大小数据来源:《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》,简称“十四五”规划纲要。纲要显示,2019年数据实际情况为77.3岁。。“十四五”规划中人均预期寿命也被列为预期性指标,对2025年的目标没有提出具体的规划要求。虽然对平均预期寿命不断增长的目标和方向不变,但具体到未来社会经济发展能够使得平均预期寿命有多大的变化,却是一个非常困难的研究问题,特别是不同区域或省际之间如何设定规划目标困难重重:目标太低,很快实现了,目标太高,又无法判断是否确实难以达到,很难确认是预测出现很大偏差还是基础数据问题引起的误判。平均预期寿命规划目标难以确定一方面是对平均预期寿命的状况水平测量结果有很大争议,婴儿死亡率数据质量问题突出[2-3],特别是在人口规模较少或调查样本较小的情况下,死亡数据可能偏差很大;另一方面是对平均预期寿命预测结果的可靠性存在疑问,直接通过时间序列数据对平均预期寿命进行模型外推,还是通过预测年龄别死亡率结果再推算平均预期寿命[4-5]?因此,科学测量和准确预测平均预期寿命的基本状况和变化趋势,不仅具有重要的科学研究价值,同时也具有非常重要的现实意义。
二、文献综述
平均预期寿命是人口分析的关键指标之一,是人口预测模型的基础。对平均预期寿命的预测关系到人口预测模型的质量。平均预期寿命参数估计方法与普通预测既有相同的一面,又有不同的一面。相同之处在于可以采用历史数据建立回归模型,然后进行趋势外推。不同之处在于不同人口所处的发展阶段不同,可以通过已有其他人口作为重要的基础数据,进行回归建模,然后进行参数预测,比如模型生命表方法就属于这类应用,这个做法通常是解决现有人口基础数据质量不高或时间序列数据相对较少的问题。
平均预期寿命预测包括两部分研究工作,第一部分是对年龄别死亡率的预测,第二部分是根据预测的年龄别死亡率建立相应的生命表,从而得到平均预期寿命的预测结果。平均预期寿命的预测首先需要解决年龄别死亡率的预测问题。对年龄别死亡率的预测通常采用LeeCarter 模型[6]。LeeCarter 模型是该领域研究最典型的方法,对死亡率随机预测研究影响巨大,世界各国的相关应用和方法改进文献不计其数[7-11]。
回顾中国预期寿命研究的历史,基础数据收集主要是人口普查、1%人口抽样调查和年度1‰人口变动抽样调查,基础数据质量和数量都受到很大限制,因此多数应用是根据模型生命表进行经验估计。2000年以来,特别是2010年以来,对年龄别死亡率的预测研究随着基础数据的不断丰富而开始有很多文献[12]。然而,对于平均预期寿命的预测主要是采用LeeCater模型,多数研究也仅限于对中国年龄别死亡率预测方法方面的基础应用研究。有学者研究认为,在我国死亡率数据较少的背景下,以LeeCater模型为框架的随机死亡率预测模型效果欠佳[13],但对预测效果欠佳的具体情况和面临的问题并没有非常详尽的文献描述。与此同时,有些研究也是采用了LeeCater模型为框架的随机死亡率预测模型,而且采用的数据也很少,仅仅是1992—2002年(不含1995年),研究认为LeeCater模型对中国死亡率数据具有很好的拟合效果[14],两类研究之间的矛盾确实令人匪夷所思。此外,还有一些研究提出有限数据死亡率的建模方法和中国的具体应用[15-16]。随着死亡率数据的增加,预测模型效果是否有所改善,效果如何,都需要认真研究和深入探讨。此外,LeeCater模型在中国具体应用过程中,很少涉及对不同年龄预期寿命预测结果的进一步讨论或预测结果的实证检验。
有研究認为,利用人口统计数据建立LeeCater死亡率模型对于预测误差的控制通常采用简单外推方法,存在系统的低估偏差[17]。即使是对死亡率随时间变化的速度(kt)分布进行区间估计的方法,由于基础模型在很大程度上决定了模型误差的大小,因此,需要进一步改进模型。特别是在应用过程中,反而忽略了基础数据本身对预测偏差的影响。2019年有学者提出通过对基础数据进行平滑的方法来控制数据的偏差[18]。总之,提升预测结果的科学性、可靠性的主要方法无非是改善输入数据的质量和改进预测方法,解决问题的途径通常是从理论和实践两个方面进行努力。
三、LeeCarter 模型与简略生命表算法
虽然目前国内有很多学者采用中国或国外数据对LeeCarter模型进行了一些相关应用研究,但绝大多数研究采用国外学者编制的R语言程序,并没有对算法的实际计算过程和所有细节进行重复演算或验证,包括对LeeCarter模型1992年出现的经典文献[6]也没有进行仔细的重复检验,同时,在研究过程中,还存在为了模型拟合“效果”舍弃重要可获得数据的现象。
本文采用Python语言对相关研究进行重复检验,并对计算过程的细节进行尽可能完整的描述,目的是在检验LeeCarter模型的同时,补充一些文献对关键算法语焉不详或订正相关研究可能存在的缺陷或错误,也有利于研究者对本研究进行重复检验。
1. LeeCarter模型算法
LeeCarter 模型参数估计主要是采用经典的SVD分解方法、加权最小二乘方法和极大似然估计方法。在只有年龄别死亡率时间序列数据的情况下,也可以使用最小二乘方法进行参数估计。
2. 简略生命表算法
生命表是平均预期寿命估计的标准化方法。由于采用的基础数据不同,生命表可以分为简略生命表和完全生命表两种。完全生命表是单岁年龄分组为基础数据,而简略生命表则主要是采用5岁年龄分组的数据。由于受数据质量的限制,本项研究采用简略生命表进行预期寿命的估计,具体算法见笔者2009年的研究[20]。
總之,采用LeeCarter模型进行平均预期寿命预测需要完成四个步骤:第一步,通过历史数据对αx、βx和kt进行参数估计;第二步,对kt进行预测,预测的方法可以采用时间序列回归或自回归模型;第三步,对年龄别死亡率进行预测,使用αx、βx和预测的kt对nmx, t进行预测;第四步,通过预测nmx, t得到平均预期寿命预测结果。
四、数据来源与面临的问题
中国历史上虽然有悠久的人口登记传统,但规范的现代人口基础数据收集还是从1949年以来才开始的。从死亡率变动模型研究的角度看,可供使用的中国人口死亡数据还是存在以下几个方面的问题。
第一,死亡数据比较缺乏。虽然自1953年第一次全国人口普查以来,我国经历了多次人口普查、1%人口抽样调查和年度1‰人口变动抽样调查,但与其他数据相比,死亡方面的数据还是比较缺乏的。比如,1982年以前的人口普查没有收集死亡数据。1982年人口普查才开始系统收集年龄别人口死亡数据,而1982年人口普查死亡数据与年龄结构时点数据还存在半年的差距,即收集了1981年的死亡人口情况,在数据的使用过程中面临很多困难需要解决。1986年我国开始公布年龄结构及其年龄别死亡人口数,从时间序列以及对于研究年龄别死亡率变动规律来说,目前收集的死亡人口数据还是比较缺乏的。特别是,由于时间序列模型是对不规则因素进行分析,所以样本点不能过少,至少应该在30个以上[19],我国的人口死亡数据还不能满足这一点。
第二,公布数据标准化程度不高。比如1986年及以后公布的死亡人口数据,有些年份公布的年龄组截至100岁及以上(100+),有些年份的年龄组截至85岁及以上(85+),还有些年份的年龄组截至90岁及以上(90+)。且不论数据质量如何,在数据使用过程中,仍然面临时间序列数据缺失或完整性问题。
第三,单岁年龄组数据缺失问题越来越突出。由于年度人口变动抽样调查的抽样比在1‰左右,而死亡是一个小概率事件,特别是死亡率较低或人口数据较少的个别单岁年龄组,经常会出现抽样死亡人口数为0的情况,随着年龄别死亡率的下降,这个问题会越来越突出。
第四,数据质量问题不同程度地存在。对中国婴儿死亡率数据质量问题和漏报问题的研究由来已久。国家卫生统计系统公布的婴儿死亡率一直高于国家统计局人口普查或抽样调查公布的数据,而且两者的差距不断扩大,比如,国家统计局人口抽样调查公布的1994年婴儿死亡率为38.79‰,而《中国卫生统计年鉴》公布的婴儿死亡率为39.9‰,两者相差1‰左右,相对误差不到3%。国家统计局人口普查公布的2000年婴儿死亡率为26.90‰对第五次人口普查死亡数据修正后重新计算,修正后2000年婴儿死亡率为28.41‰,见《人口和计划生育常用数据手册(2018)》。,而《中国卫生统计年鉴》公布的2000年婴儿死亡率为32.2‰,两者的差距扩大到5‰以上,相对误差近20%。国家统计局人口普查公布的2010年婴儿死亡率为3.82‰,《中国卫生统计年鉴》公布的2010年婴儿死亡率为13.1‰,两者的差距达到3.43倍。可见,随着婴儿死亡率的下降,国家统计局人口普查数据与国家卫生统计系统公布数据之间的差距越来越大,这必然影响到对模型估计可靠性的判断。因此,采用国家统计局人口普查或抽样调查公布的年龄别死亡数据进行模型拟合时,需要特别注意对预期寿命高估和模型过度拟合所带来的更大误差或错误风险。
由于受数据的连续性和可获得性的限制,本项研究采用1994—2019年全国人口普查、1%人口抽样调查和年度1‰人口变动抽样调查数据。其中,1996年的数据为0—85+,为了与多数年份人口变动抽样调查数据年龄组一致,即0—90+,将人口普查、1%人口抽样调查90岁及以上人口数据合并,同时,对1996年85—89岁和90岁及以上数据进行估计。为了避免单岁年龄组数据缺失或数据不稳定问题,采用5岁组数据。此外,对0—4岁年龄组进一步细分为0岁和1—4岁两个年龄组,对90岁及以上进行合并。
五、中国人口平均预期寿命预测
采用LeeCarter模型进行中国平均预期寿命预测的关键是通过时间序列历史数据对参数αx、βx和kt进行估计,特别是对kt的估计和预测。下面将通过实际数据对模型的估计结果进行检验,并以此为基础,对中国人口平均预期寿命预测结果进行分析。
1. LeeCarter模型参数估计
首先看αx的估计结果。由于年龄别死亡率的性别差异很大,因此,αx性别差异明显。从0岁、1—4岁年龄组开始,αx的性别差异逐渐增大,到35—39岁达到最大,随后逐渐减小。从80岁开始,两者的差距明显缩小。另外,采用极大似然估计方法对αx进行重新估计,但估计结果与SVD方法估计的结果差别不大(见图1)。
其次看βx的估计结果。从不同方法对βx的估计来看,经典的LeeCarter模型SVD分解得到的βx与极大似然估计或加权最小二乘法之间还是存在明显差别的。差别主要是表现在三个方面:第一方面差别是男女之间女性差别更大一些;第二方面差别主要表现在0岁、10—34岁;第三方面是SVD方法0岁βx明显比其他两种方法低,而10—34岁比其他两种方法高(见图2)。
总之,由于不同方法估计的αx的差距相对较小,而不同方法估计的βx和kt差距相对较大,其含义是在LeeCarter模型参数估计过程中,βx和kt作为模型参数是模型构建的关键,也是基础模型差别的重要原因。也就是说,死亡率随时间变化的时期因子kt和年龄因子βx估计对模型产生重要的影响。
2. 预测可靠性的历史数据检验
为了检验中国人口平均预期寿命预测方法的可靠性,根据1994—2015年调查数据建立预测模型,然后,根据模型预测2016—2019年中国人口平均预期寿命,再将预测结果与实际调查数计算的平均预期寿命进行比较,这个比较的前提是假定国家统计局基础调查数据反映的趋势和模式可靠。
(1)回归模型。LeeCarter模型用于年龄别死亡率预测主要是估计kt,本项研究采用经典的LeeCarter模型对αx、βx和kt进行估计,通过一元线性回归方法建立时间与kt的相互关系,回归模型参数见表1。从表1可以看到,1994—2015年中国人口无论男性还是女性,历史数据kt与时间高度相关。男性和女性的相关系数都在92%以上,男性相关系数为92.4%,女性为94.2%。可见,女性的相关系数更高一些。从自变量回归系数来看,女性kt随时间下降的速度为-1.0424,比男性的-0.7497更快一些,也就是说,现有历史數据中女性年龄别死亡率的时期敏感性比男性更高一些,即在人口平均预期寿命的提高过程中,女性更快一些。
(2)历史数据拟合。为了充分看到模型对历史数据的拟合效果,下面从年龄别死亡率和人口平均预期寿命两个方面来进行分析。
首先来看死亡率的拟合。从总体上看,对于不同的年份,无论男性还是女性,年龄别死亡率拟合数据与实际调查数据的年龄别变化趋势还是非常一致的(见图4)。
从时期的角度看,除了人口普查和1%人口抽样调查的相对误差较小外,1994—2015年随着死亡水平的降低,各年龄组年龄别死亡率相对误差有明显的增加趋势(见表2)。1994年各年龄组年龄别死亡率平均相对误差男性为10.63%,女性为18.42%,到2015年分别上升到17.73%和18.31%。各年龄组年龄别死亡率平均相对误差时期变化的明显特征是,在波动上升的过程中,人口普查年份各年龄组年龄别死亡率平均相对误差相对较低,比如2000年男性为5.13%,女性为8.80%,2010年男性为7.43%,女性为7.84%,明显低于1%人口抽样调查年份各年龄组年龄别死亡率平均相对误差,比如1995年男性为6.03%,女性为7.89%,2005年男性为10.11%,女性为4.30%。同样,人口普查和1%人口抽样调查年份的各年龄组年龄别死亡率平均相对误差明显低于1‰人口变动抽样调查(见表2)。
从队列的角度看,不同时期各队列死亡率平均相对误差较小的年龄组为40—84岁,男性和女性各队列死亡率平均相对误差在11%以内,拟合比较差的是0岁组(见表3),男性0岁组平均相对误差超过20%,女性0岁组平均相对误差超过30%。1994—2015年0岁人口死亡率表现出明显的大起大落(见图5)。1994—2015年中,有9年的0岁死亡率比上一年的水平上升,其中,1997年、2006年、2008年和2011年发生了0岁人口死亡率非常明显的上升,2008年上升或许和汶川地震有关,但其他年份难以解释。此外,从男性和女性各年龄组的拟合数据来看,女性拟合效果比男性差一些,原因是女性的死亡率比较低,测量的相对误差更大一些。
不同年龄的死亡率不同,而从年龄别死亡率与平均预期寿命之间的关系来看,低年龄组年龄别死亡率对出生人口平均预期寿命的影响更大,其他年龄组只影响平均预期寿命的余寿。虽然在年龄别死亡率变化过程中,0岁人口的死亡率远远低于老年人口,但0岁人口死亡率的变动将会影响到其他各个年龄的平均预期寿命。0岁人口死亡率的大起大落必然引起出生人口平均预期寿命的明显波动。因此,0岁人口死亡率的数据质量和模型拟合在平均预期寿命推算和预测过程中非常重要。
其次来比较人口平均预期寿命的差别。出生人口平均预期寿命是预期寿命最重要的指标,需要进行细致的分析。如图6所示,无论男性还是女性,虽然两者的出生人口平均预期寿命有一定的差距,但模型推算预期寿命与实际调查预期寿命的相对误差都在2.05%以内,有一半以上的年份在1.0%以内,绝大多数年份在1.5%以内,相对误差较大的年份为1995、2000、2006、2014和2015年。男性出生人口平均预期寿命的平均相对误差为0.7184岁,女性出生人口平均预期寿命的平均相对误差为0.7282岁。从出生人口平均预期寿命的变化趋势来看,随着时间的变化,个别年份平均预期寿命大幅度上升(如2001、2006、2009、2015年)或下降(如1997、2008、2010年),尤其是大幅度下降与平均预期寿命的变化规律相违背。根据世界各国平均预期寿命变化的历史数据,在没有战争、大范围自然灾害、瘟疫或饥饿情况下,平均预期寿命大幅度下降是不太可能的。同样,没有显著的疾病防治水平突破性进展或营养健康水平的大幅度改善,平均预期寿命大幅度提升也是不太可能的,这反映了基础数据在模型建立过程中的问题或缺陷。
为了反映模型拟合情况,可以从时期和队列两个方面进行观察:从时期(各年度)的角度观察模型拟合各队列(年龄组)平均预期寿命的平均相对误差的大小,从队列(各年龄组)的角度可以观察各时期(年度)平均相对误差的大小。
从时期的角度看,除了人口普查和1%人口抽样调查的相对误差较小外,1994—2015年随着预期寿命的提高,各年龄组平均预期寿命的相对误差有明显不断增加的趋势(见表2)。1994年各年龄组平均预期寿命的平均相对误差男性为0.6%,女性为1.31%,到2015年分别上升到5.18%和5.05%,其中2006年的平均相对误差最大,男性为9.05%,女性为7.23%。误差在波动上升的过程中,1%人口抽样调查和人口普查年份各年龄组平均预期寿命的平均相对误差相对较低,比如2005年男性为0.87%,女性为0.42%,2010年男性为1.53%,女性为2.37%等等。
从队列的角度看,0岁人口平均预期寿命的平均相对误差最小,男性为0.97%,女性为0.94%,随着年龄的增加,无论男性还是女性平均预期寿命的平均相对误差不断增大,到90岁及以上分别增加到13.80%和11.36%(见表3)。增加的原因在于在平均预期寿命生命表中T (x)是剩余存活人年数,由于0岁人口平均预期寿命是各队列死亡概率或存活人年数累计结果的反映,因此,由于各队列误差相抵的原因,累计的误差相对较小。根据这个特性,在平均预期寿命预测结果的使用过程中需要注意的是,虽然随着年龄增加,平均预期寿命在不断下降,预测的绝对误差可能保持不变或不断减小,但相对误差逐渐增大的特征和性质不变。
(3)模型预测与实际调查对比。历史上数据建模以及对模型检验的目的是检验LeeCarter模型对中国人口死亡率历史数据拟合的可靠性和存在的问题。为了进一步检验LeeCarter模型在中国人口平均预期寿命预测中的可靠性,可以根据历史数据建立的模型进行预测,并与实际数据结果进行比较。
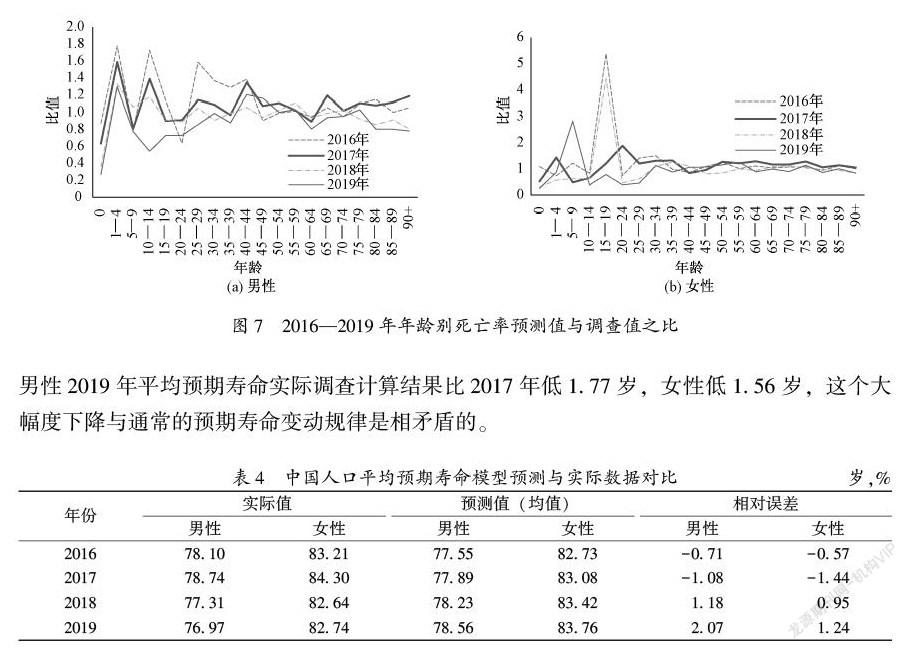
首先来看年龄别死亡率预测的情况。男性年龄别死亡率模型预测值比实际调查年龄别死亡率高的年龄组主要是1—40岁,0岁人口的预测值明顯低于调查值(见图7),2016年预测数据的差距最明显,其他年份的数据相对好一些。女性与男性不同,2016年和2018年15—19岁和2019年5—9岁年龄组出现了明显调查异常值。由此可见,随着死亡水平的下降,1‰人口变动抽样调查年龄别死亡率数据将越来越多地面临这个测量问题。
其次来检验人口平均预期寿命。根据1994—2015年数据建立回归模型,对2016—2019年中国人口平均预期寿命进行预测,预测结果见表4。从表4可以看到,通过回归模型计算年龄别死亡率然后建立简略生命表,得到的平均预期寿命预测值与实际调查值计算的平均预期寿命的相对误差在2.1%以内,总体上,男性的相对误差比女性大一些。特别需要指出的是2018年和2019年实际调查值计算的平均预期寿命低于预测值,而且处于连续下降趋势,男性2019年平均预期寿命实际调查计算结果比2017年低1.77岁,女性低1.56岁,这个大幅度下降与通常的预期寿命变动规律是相矛盾的。
总之,虽然不同年龄死亡率预测结果与调查值之间存在的差距不同,而且40岁人口的波动比较大。由于误差相抵的原因,出生人口的平均预期寿命与实际调查推算值之间存在误差,但误差的范围在2%以内。模型预测与调查值之间的差别一方面反映了模型拟合需要改进的问题,另一方面也说明数据质量本身面临的困难和导致的问题。如果调查数据精度很高,那么,不太可能出现平均预期寿命的大幅度下降或上升,也不太可能发生婴儿死亡率的大幅度上升,考虑到与国家卫生统计系统婴儿死亡率的一致性,因此,在基础数据和模型应用过程中,需要对基础数据和模型的偏差方向有一个基本的判断和正确的理解。
3. 未来预期寿命预测
根据1994—2015年基础数据和LeeCater模型参数估计,对未来中国人口的年龄别死亡率进行预测,然后得到不同年龄的平均预期寿命。在生命表构建的指标中,出生人口平均预期寿命、老年人口平均预期寿命以及高龄老人平均预期寿命是非常重要的指标。关于老年人口的界定,考虑到中国法定退休年龄,提供60岁和65岁两个统计口径。虽然预测模型可以提供平均预期寿命的95%置信区间,但考虑到死亡人口漏报对死亡率低估以及国家统计局调查数据的偏差问题,实际平均预期寿命预测结果高估的可能性很大。为了避免系统性高估,本项研究认为平均预期寿命预测结果在预测值的下限和均值之间的可能性更大。下面将分别对男性和女性平均预期寿命的预测结果进行分析。
(1)男性平均预期寿命。首先,从男性出生人口平均预期寿命的预测下限来看,2020年预测的下限为76.35岁,预计到2030年提高到79.11岁,10年提高2.76岁,平均每年提高0.28岁。60岁男性人口平均预期寿命从2020年的20.72岁提高到2030年的22.63岁,提高1.91岁。80岁男性人口平均预期寿命从2020年的8.01岁提高到2030年9.11岁,提高1.1岁。从平均预期寿命的构成和变化来看,2020年男性60岁平均预期寿命占出生人口平均预期寿命的27.28%,2030年提升到28.61%;80岁平均预期寿命占出生人口平均预期寿命的10.58%,2030年提升到11.52%;由此可见,男性60岁平均预期寿命提高的幅度占出生人口平均预期寿命提升比例的69.20%,而且平均预期寿命的提高主要是60岁及以上人口提升更加迅速形成的(见表5)。
其次,从男性出生人口平均预期寿命的预测均值来看,2020年预测的均值为78.89岁,到2030年提高到82.01岁,提高3.12岁,平均每年提高0.31岁;60岁男性人口平均预期寿命从2020年的22.47岁提高到2030年的24.87岁,提高2.4岁;80岁男性人口平均预期寿命从2020年的8.87岁提高到2030年10.47岁,提高1.46岁。同样,从平均预期寿命构成的比例及其变化来看,2020年男性60岁平均预期寿命占出生人口平均预期寿命的28.48%,2030年提升到30.33%;80岁平均预期寿命占出生人口平均预期寿命的11.42%,2030年提升到12.77%;尽管男性人口预测均值相对于下限来说变化的幅度相对大一些,但两者的结构变动特征不变。
再次,从均值与下限差距来看,2020年预测的均值与下限相差2.54岁,到2030年扩大至2.9岁。从平均预期寿命历史变化的平均速度来看,预测的下限与均值两者的差距相当于平均预期寿命增长需要8—9年的时间。
(2)女性平均预期寿命。女性和男性平均预期寿命的最大差别是女性出生人口平均预期寿命明显高于男性。增长速度通常也是女性快于男性,其结果是随着预期寿命的提升,两者的差距扩大。
首先,从女性出生人口平均预期寿命的预测下限来看,2020年预测的下限为81.87岁,预计到2030年提高到84.74岁,比2020年提高2.87岁,平均每年提高0.29岁。60岁女性人口平均预期寿命从2020年的24.30岁提高到2030年的26.39岁,10年间提高2.09岁。80岁女性人口平均预期寿命从2020年的9.70岁提高到2030年的11.00岁,提高1.3岁。与男性相比,女性提高的幅度更大一些,出生人口平均预期寿命下限的差距从2020年的5.52年提高到2030年的5.63年。从平均预期寿命构成的比例来看,2020年女性60岁平均预期寿命占出生人口平均预期寿命的29.68%,2030年提升到30.99%;80岁平均预期寿命占出生人口平均预期寿命的11.85%,2030年提升到12.86%。从提高的幅度来看,女性人口60岁平均预期寿命提升幅度占出生人口平均预期寿命提升幅度的72.82%(见表6)。
其次,从女性出生人口平均预期寿命的预测均值来看,2020年预测的均值为84.1岁,到2030年提高到87.25岁,提高3.15岁,平均每年提高0.32岁;60岁女性人口平均预期寿命从2020年的25.89岁提高到2030年的28.45岁,10年间提高2.56岁;80岁女性人口平均预期寿命从2020年的10.68岁提高到2030年的12.41岁,提高1.73岁。同样,从平均预期寿命构成的比例和变化来看,2020年女性60岁平均预期寿命占出生人口平均预期寿命的30.78%,2030年提升到32.61%;80岁平均预期寿命占出生人口平均预期寿命的12.84%,2030年提升到14.23%;与男性类似,预测下限相对于均值来说变化的幅度相对小一些,但女性两者的结构变动特征不变。而且,平均预期寿命的提高主要是60岁及以上人口提升更加迅速形成的。
再次,从均值与下限差距来看,2020年预测的均值与下限相差2.23岁,到2030年扩大至2.51岁。从女性平均预期寿命变化的历史速度来看,两者的差距相当于7—8年的增长幅度,与男性相比女性稍快一些。
总之,死亡人口的数据质量问题是影响未来人口平均预期寿命预测的基础性因素,与其他数据不同,死亡人口漏报的可能性远远大于重报,更不太可能存在利益驱动的多报。因此,目前收集到的死亡人口数低估的可能性远远大于高估的可能性。特别是《中国卫生统计年鉴》公布的婴儿死亡率不仅一直高于国家统计局人口普查和抽样调查推算的数据,而且两者的差距无论是绝对差距还是相对差距都随着死亡水平的下降而逐渐扩大。考虑到低龄人口死亡是一个小概率事件,因此,死亡率或死亡概率的计算对分子漏报非常敏感,且具有死亡水平越低,漏报对相对误差影响越大的特点。因此,采用现有数据及其所构建的模型为基础,对未来中国人口平均预期寿命预测结果的估计处于均值與下限之间,或更接近下限的可能性要大一些。
六、研究结论与讨论
中国人口平均预期寿命预测不仅是人口科学研究的难题,同时,也是相关应用研究的难题。研究困难既涉及基础数据的质量问题,也涉及模型实际应用的问题。通过对中国1994年以来死亡基础数据的研究和LeeCarter死亡率模型应用,本项研究得出以下几个基本结论。
第一,虽然中国死亡数据收集能力有了很大的改进和提升,但死亡数据质量和数据之间的冲突和矛盾依然比较明显。国家统计局的时间序列数据与国家卫生统计公布数据之间的差距加大。
第二,男性死亡率相对较高,但与男性的数据质量相比较,女性调查数据的相对误差可能更大。随着死亡水平的下降,1994年以来,现有1‰人口变动抽样调查年龄别死亡率数据面临越来越严重的数据质量问题。
第三,LeeCarter死亡率模型在中国年龄别死亡率中平均相对误差较小的年龄组为40—84岁,拟合比较差的是0岁组。由于0岁人口死亡率的变动将会影响到其他各个年龄的平均预期寿命,0岁人口死亡率的大起大落必然引起出生人口平均预期寿命的明显波动。因此,0岁人口死亡率的质量和模型拟合结果在平均预期寿命推算、预测过程中非常重要。
第四,LeeCarter死亡率模型在中国年龄别死亡率预测过程中,需要对基础数据进行深入研究和必要的调整,模型应用的关键既有基础质量的问题,也有模型构建的问题。考虑到中国历史数据的质量问题,在没有科学调整数据的前提下,在建模过程中需要考虑并防止模型对基础数据的过度拟合问题。由于死亡人口重报,特别是多报的可能性很小,因此现有数据和模型对平均预期寿命的估计肯定是一个高估。
第五,尽管中国死亡历史数据存在一些缺陷,但由于年龄别死亡率数据误差相抵的原因,对出生人口平均预期寿命推算的结果误差明显下降。因此,在数据应用过程中,对不同年龄人口平均预期寿命的相对误差或绝对误差需要区别对待。
LeeCarter死亡率模型在世界各国死亡率预测中应用广泛,在中国也有很大的基础研究和实际应用价值。在模型的应用过程中,需要充分考虑基础数据的来源和数据质量的差距问题,由于高龄人口年龄别人口数比较少,观察数据的稳定性和数据质量问题更加突出,特别是长期预测时,因为90岁及以上或100岁及以上数据缺乏或粗略,长期预测可能面临现有基础数据和模型应用的缺陷或其他问题。此外,为了解决低龄模型估计误差和婴儿死亡率数据质量带来的误差问题,进一步提高数据的稳定性,研究时往往采用时间序列数据平滑、贝叶斯估计等方法,这些方法理论上必然会对统计推断和模型应用的改进有很大的帮助,但也需要防止人为过度拟合的问题。因此,针对中国人口平均预期寿命预测面临的问题,今后还需要更多的理论、方法和中国实证研究来加以完善。
总之,本项研究的主要目的是在中国现有数据条件下考察应用LeeCarter模型所面临的问题和挑战,尝试对中国人口平均预期寿命的变化趋势和水平提供一个估计,从而形成与经验估计或趋势外推结果的对照和互验,避免在中国平均预期寿命实际变化趋势或水平研究过程中由于研究者仅凭主观想象或判断而可能引起的严重偏差与误判。
参考文献:
[1]DAVID S, NATHAN K. Mathematical Demography [M]. Berlin: Springer-Verlag, 1977: 1-2.
[2]黄荣清,曾宪新.“六普”报告的婴儿死亡率误差和实际水平的估计[J].人口研究,2013(2):3-16.
[3]黄润龙.1991—2014年我国婴儿死亡率变化及其影响因素[J].人口与社会,2016(3):67-75.
[4]OEPPEN J, VAUPEL J W. Broken limits to life expectancy[J]. Science, 2002, 296(5570):1029-1031.
[5]LEE R D. Mortality forecasts and linear life expectancy trends[EB/OL].[2003-03-25].https://escholarship.org/uc/item/3sd9m7d5.
[6]LEE R D, CARTER L R. Modeling and forecasting U.S.mortality[J]. Journal of the American Statistical Association, 1992,87(419): 659-671.
[7]LAWRENCE R C. Forecasting U.S.mortality: a comparison of BoxJenkins ARIMA and structural time series models[J].The Sociological Quarterly, 1996, 37(1): 127- 144.
[8]BOOTH H. Demographic forecasting: 1980 to 2005 in review[J]. International Journal of Forecasting, 2006,22(3): 547-581.
[9]Egle· Ignataviiūte·, Rasa Mikalauskait e·-Arminien e·, Jonas iaulys.Lee-Carter mortality forecasting[J]. Lithuanian Journal of Statistics, 2012,51(1): 22-35.
[10]張秋芸.LeeCarter模型在死亡率预测中的应用[J].统计学与应用,2015(3):155-161.
[11]Csar Neves, Cristiano Fernandes, Henrique Hoeltgebaum.Five different distributions for the Lee-Carter model of mortality forecasting: a comparison using GAS models[J]. Insurance: Mathematics and Economics, 2017, 75(4):48-57. [12]卢仿先,尹莎.LeeCarter方法在预测中国人口死亡率中的应用[J].保险职业学院学报,2005(6):9-11.
[13]王晓军,赵明.中国高龄人口死亡率随机波动趋势分析[J].统计研究,2014(9):51-57.
[14]李志生,刘恒甲.LeeCarter死亡率模型的估计与应用——基于中国人口数据的分析[J].中国人口科学,2010(3):46-56.
[15]韩猛,王晓军.LeeCarter模型在中国城市人口死亡率预测中的应用与改进[J].保险研究,2010(10):3-9.
[16]王晓军,任文东.有限数据下LeeCarter模型在人口死亡率预测中的应用[J].统计研究,2012(6):87-94.
[17]吴晓坤,李姚洁.LeeCarter模型外推预测死亡率及偏差纠正[J].统计与决策,2016(20):19-21.
[18]CARLO G. Smooth constrained mortality forecasting[J]. Demographic Research, 2019,41(38):1091-1130.
[19]孙佳美.生命表编制理论与实验[M].天津:南开大学出版社,2013:122-126,132.
[20]王广州.Python人口统计[M].广州:广东高等教育出版社,2019:87-97.
[责任编辑 武 玉 ]
