基于区间两阶段抗风险随机规划的绿洲水资源优化配置

习凯燕，虞佳陆，张 敏，于瑞德,3

(1.中国科学院新疆生态与地理研究所，荒漠与绿洲生态国家重点实验室，新疆 乌鲁木齐 830011；2.中国科学院大学，北京 100049；3.烟台大学环境与材料工程学院，山东 烟台 264005)

在经济发展日趋增长的今天，水资源已成为制约经济稳定和发展的重要影响因子，特别是在我国极度缺水的西北地区[1-2]。绿洲作为西北干旱区特色农业发展模式，一直以来都受到政府和学术界的密切关注。位于干旱区内策勒河下游绿洲重要特征是：“有水便为绿洲，无水便为荒漠”[3-5]，不仅反映了干旱区绿洲生态系统的脆弱性，也表明了水资源对绿洲发展的重要程度[6-7]。策勒绿洲主要由三大区域组成：生态区-防护林、农业区和居民区，分别对应着生态需水、农业需水和生活用水。其中，农业用水占绿洲总用水量的90%以上。然而，由于人口增长和耕地的不断扩张，农作物用水的竞争也日趋激烈。因此，合理分配农业水资源、提高用水效率是缓解绿洲农业用水矛盾、维持绿洲生态稳定、促进绿洲经济可持续发展的主要解决方式[8]。

在水资源优化配置中，存在着许多不确定性。水资源管理的决策者需要在未知下一年可用水量的前提下，对不同需水用户，如工业、市政、农业等，制定下一年的预供水计划，以便各用户安排下一年的生产生活；等到下一年到来，根据实际的来水情况，决策者需要对预供水计划做出相应调整，制定实际供水计划。若实际供水量与预供水量一致，则各用户所安排的生产活动能够按计划进行，从而产生一定的效益；反之则会带来相应的损失。针对这一问题，许多学者都提出了建设性的方法。其中，一种典型方法是由黄国和等[9]提出的区间参数两阶段随机优化方法(Interval Two-stage Stochastic Programming, ITSP)。

这一方法被广泛用于水资源管理中，尤其是灌区水资源配置问题[10-14，16]。与此同时，众多学者在黄国和等[9]的研究基础上，对区间参数两阶段随机优化方法进行了进一步的发展与创新，主要方向有两个：(1)向着多水资源联合调度、多区域共同调水的趋势发展[10-11]。付银环等[10]在综合考虑地表水-地下水联合调度的条件下，用ITSP模型结合作物全生育期水分生产函数建立多阶段、多目标水资源优化分配模型，来求解灌区水量最优分配方案。李晨洋等[11]以灌区多水源联合调度系统收益最大为目标函数，构建ITSP模型对地表水和地下水在各作物之间的配水目标进行优化。(2)把抗风险方法引入到ITSP模型中，以使得系统在应对风险方面更加稳健。在ITSP模型中，用期望来评估未来收益，而理论上说，期望是对多种随机情景的一种加权平均，因此它是风险中性的，一旦发生极端情况，如遭遇旱季或巨大洪灾，将会使得用户遭到巨大损失[12]。因此，把抗风险方法引入到ITSP模型中，可以得到应对风险更加出色的系统。陈红光等[13]通过引入鲁棒系数来表达风险测度，结合ITSP模型解决区域配水问题。付强等[14]运用GCMS模型模拟了未来的温度和降水，将ITSP与基于条件风险价值(Conditional Value at Risk，CVaR)的风险规避方法相结合来求解三种气候背景下灌区水资源分配的策略。张敏等[12]用CVaR代替期望提出了新的ITSP-CVaR模型。此外，由于传统求解ITSP模型的交互式解法可能存在最优目标收益区间跨度大的缺陷，张敏等[15]基于灰度线性规划的最新解法，提出了一个求解ITSP-CVaR模型的新方法，该方法可通过单一参数的调节，缩短最优目标收益区间，从而帮助决策者制定更加贴合其主观风险偏好的决策计划。

对于干旱区绿洲农业灌水问题，申梦阳等[16]根据策勒绿洲作物的需水情况，使用ITSP模型研究了绿洲作物按季节配水的最优策略。然而，由于策勒绿洲处于极端干旱区，只有一条外来河流作为补给源，加之蒸发量大，故而策勒绿洲的灌溉问题存在更大的不确定性。本文将根据张敏等[12]最近提出的ITSP-CVaR模型，结合策勒绿洲特色经济果林种植和径流补给等特点，探讨策勒绿洲农业水资源的优化管理问题，并使用灰度线性规划方法求解该问题，分析相应的试验结果，以期为绿洲水资源决策者提供对风险具有更好应对能力的管理方案。

1 研究区概况与数据来源

1.1 研究区概况

策勒绿洲隶属新疆维吾尔自治区和田地区策勒县(35°17′55″～39°30′00″N,80°03′24″～82°10′00″E)，地处塔里木盆地南缘，南依昆仑山，北临塔克拉玛干沙漠，处于策勒河下游区域。策勒绿洲地域广阔，气候干旱，是典型的干旱性大陆荒漠气候，降雨量少、蒸发量大，气温日较差和年较差大，日照时间长。区域多年平均降水在34.9 mm左右，蒸发量根据策勒站20 cm口径蒸发皿测得年平均蒸发量为2 550 mm，多年平均最低温度出现在1月(-5.7℃)，最高温为7月(24.9℃)。根据策勒站提供的气象数据，策勒河的多年平均径流量为1.28×108m3,是策勒绿洲仅有的一条补给河流[17-19]。

1.2 数据来源

根据策勒站提供的资料，策勒绿洲农业区域主要种植特色经济果林和粮油料作物，其中经济果林种植面积占策勒绿洲农业总面积的88.1%以上，主要有：石榴、红枣、核桃等，占策勒绿洲农业面积的5.7%、59.4%、23.0%，且这三种经济作物的用水总量占绿洲农业总用水量的91.5%[20]。策勒绿洲农业主要灌溉时间为3—10月。因此，本文将研究的重点放在策勒绿洲三种经济果林，即石榴、红枣、核桃在3—10月的灌溉配水问题。本文从策勒水文局获取了策勒河近60 a的径流数据，并基于此绘制了水文频率曲线[21-22](图1)。将策勒河年径流量作为离散概率函数来处理，并根据皮尔逊Ⅲ型曲线来划分不同来水年和河流丰枯水年的发生概率，具体数据见表1。

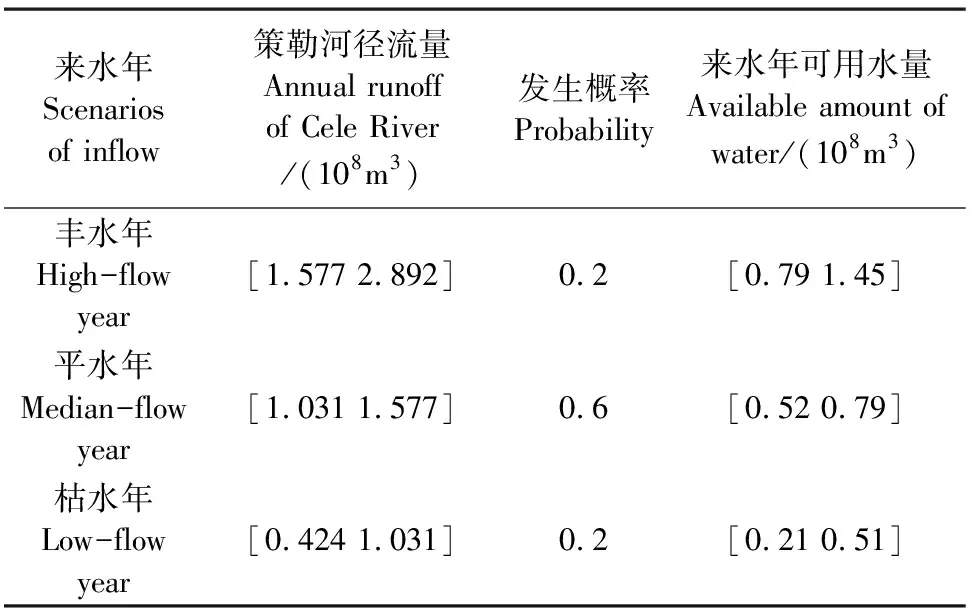
表1 不同来水年的策勒河径流量

同时，根据2013—2017年的和田地区统计年鉴[23]关于农产品市场批发价的部分数据作为策勒绿洲3种经济果林的收益和惩罚指标，通过刘姣团队在2013年提出的成本值方法来求得所需经济参数[24],并通过满足作物全生育期水量时的产量来计算减产损失[25]。

1.3 区间两阶段抗风险规划模型的建立

水量优化分配的目的是确定不同作物之间的预供水量，缓解用水矛盾，满足各作物用水需求，使目标效益最大化。本研究以策勒河径流为约束，以绿洲特色果林石榴、红枣、核桃为规划目标，建立以抗风险为前提、总收益最大化为目标的规划模型。此模型分为两个阶段：第一阶段，决策者需要在未知下一年来水量的情况下向农户告知预供水量以便农户安排下一年的生产生活；第二阶段，在已知来水量的情况下，根据实际来水量和决策者个人的风险偏好，在尽量满足各作物需水量的情况下合理配水，达到效益最大化的目标。因此，该模型的目标函数为：

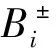
其中，t为松弛变量；α为置信水平。

约束条件如下：

(1)可用水量约束：

(2)预供水量与实际缺水水量的大小关系：

(3)预供水量的区间约束：

其中，li和ui分别表示第i种作物的最小和最大可允许供水量(107m3)。

明确目标函数和约束条件后，针对该模型可以得出它的上界子模型与下界子模型，上界子模型为：

(1)

约束条件：

(2)

(3)

(4)

(5)

下界子模型为：

(6)

约束条件：

(7)

(8)

(9)

(10)

使用张敏等[12]提出的基于灰度线性规划的权重法来求解以上模型，即求解如下的线性规划问题：

maxλf++(1-λ)f-

约束条件(2)～(5),(7)～(10)成立,并且

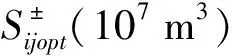
2 模型结果与分析

2.1 模型参数

表2给出了石榴、红枣、核桃三种经济果林的种植面积、单位面积需水量和年总用水量的基本信息。

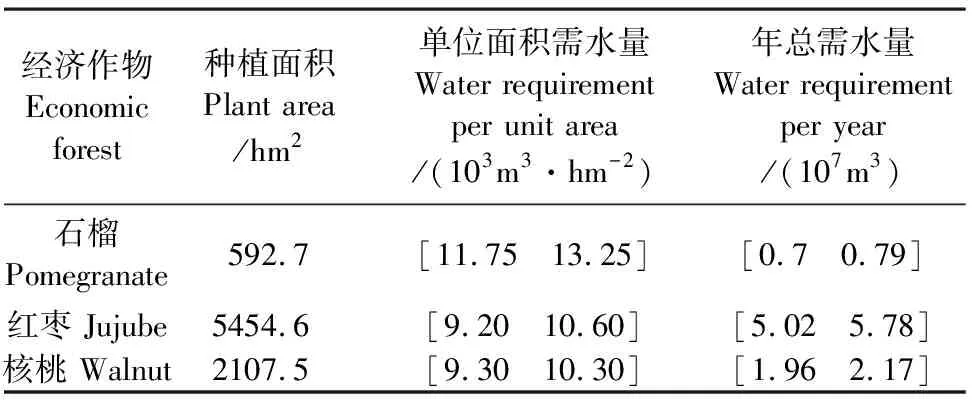
表2 绿洲三种经济果林的种植面积和单位需水量

表3给出了石榴、红枣、核桃三种经济果林的经济参数，即满足预供水量时的收益和未满足预供水量时的损失。

表3 三种经济果林的单位水量收益和惩罚

2.2 ITSP-CVaR模型中不同参数取值对结果的影响分析

首先，设定α=0，此时ITSP-CVaR模型退化为原来的ITSP模型，取参数λ=0.1，0.2,…,0.9，使用上面提到的灰度线性规划的权重方法进行求解并记录计算结果。接着设定α=0.7，依然取参数λ=0.1,0.2,…,0.9，使用上面提到的灰度线性规划的权重方法进行求解并记录计算结果。表4给出了不同λ取值下，由ITSP模型和ITSP-CVaR模型(α=0.7)得到的三种果树的预供水量和最优目标收益区间。

从表4中可以看出，无论是ITSP模型还是ITSP-CVaR模型，基于灰度线性规划的求解方法所得到的最优目标收益区间跨度都会随着λ的增大而增大，即目标收益的上界增大而下界减小。这是由于参数λ在求解过程中表示某种权重系数。较大的λ取值(靠近1)在某种程度上意味着决策者更偏重目标收益区间的上限，而较小的λ取值(靠近0)在某种程度上意味着决策者更偏重目标收益区间的下限。因此，如果决策者的主观风险偏好较为冒险，那么他很可能会更偏重目标收益的上限，从而会更倾向于选择λ较大时的配水方案；而如果决策者的主观风险偏好较为保守，那么他很可能会更偏重目标收益的下限，从而会更倾向于选择λ较小时的配水方案。由此，这种基于灰度线性规划的求解方法为不同风险偏好的决策者提供了多种选择。

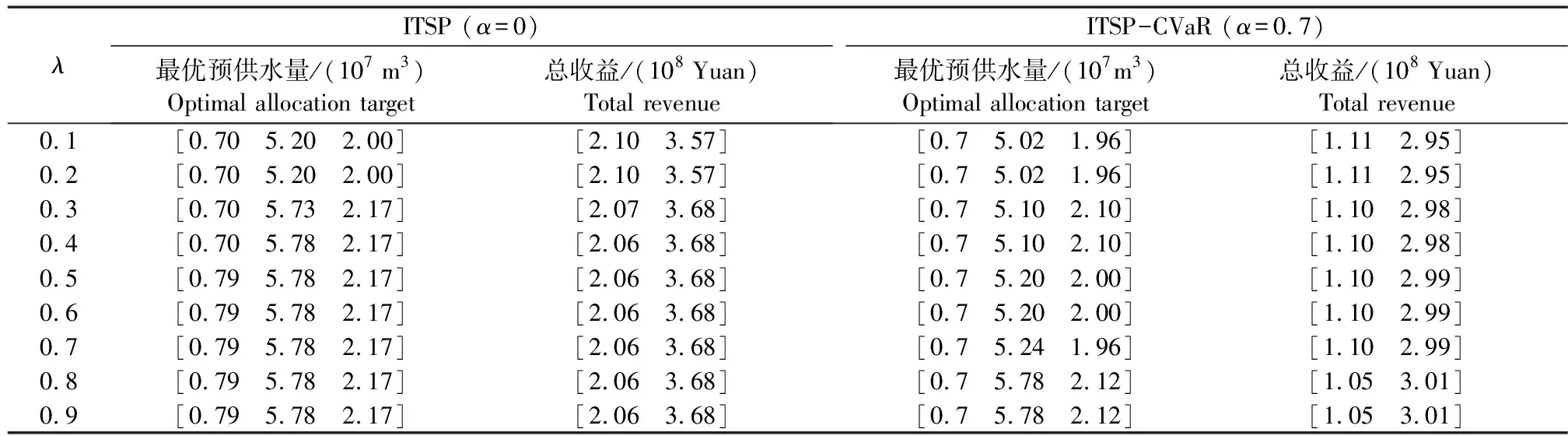
表4 不同λ时的两模型优化结果和收益

接下来，分别取定λ=0.5和λ=0.7，对ITSP-CVaR模型在α的不同取值时进行求解，并将所得结果的最优预供水量和最优目标收益罗列在表5中。从表5中可以看出，随着α的增大，最优预供水目标向着保守决策的方向变化，同时最优目标收益也随之减少。这是因为α在风险测度CVaR中表示某种风险阈值，α越大表示能够承担的风险越小，因此ITSP-CVaR模型的决策会随着α的增大而越来越保守，会以保证各作物年需水量下限为基础来争取较高收益值。同时，可以看到在同一α水平下，较小的λ对应的最优目标收益上限小于较大的λ对应的最优目标收益上限，而较小的λ对应的最优目标下限小于较大的λ对应的最优目标收益下限，这仍与之前的计算结果相吻合。综合来讲，决策者可根据自己对于风险与收益的不同偏好，通过调节参数来选择最适合自己的配水方案。

表5 不同α取值时ITSP-CVaR模型的最优配水量和收益值

由于第一阶段的预供水量决策是在未知来水情况下决定的，并且决策决定后在第二阶段不可更改，因此需要通过评估第二阶段未知事件发生时实际情况带来的结果，以此来检验模型的抗风险能力。因此，本文取定权重参数λ=0.7，分别按照ITSP和ITSP-CVaR模型(α=0.7)计算得到第一阶段的预供水量，当观测到第二阶段的实际来水情况时，最优的目标收益区间之间的比较结果展示在表6中。ITSP模型第一阶段的最优解为[0.79 5.78 2.17]，也就是石榴、红枣、核桃的预供水量分别为0.79×107m3、5.78×107m3、2.17×107m3；ITSP-CVaR模型(α=0.7)第一阶段的最优解为[0.70 5.24 1.96]，即石榴、红枣、核桃的预供水量分别为0.7×107m3、5.27×107m3、1.96×107m3。可以看出，后者给三种经济果林提供预供水量是要小于前者的，也就是说ITSP-CVaR模型相对于ITSP模型的决策更为保守。然而，根据表6可以看出，ITSP-CVaR模型在枯水年的目标收益下限比ITSP模型的收益下限高，而上限一样，即前者枯水年的收益是要优于后者的；且在平水年时ITSP-CVaR模型的下限收益也更好。因此，ITSP-CVaR模型在平枯水年的保守决策可以在稳住经济红线收益的同时，更进一步争创较高收益。所以，相比原来的ITSP模型而言，ITSP-CVaR模型在抵御风险方面更有优越性。

表6 不同来水年时ITSP和ITSP-CVaR模型的目标收益比较

2.3 三种作物最优配水量分析

设定λ=0.5、α=0.5，求解ITSP-CVaR模型，所得各经济果林在不同来水年情况下的实际供水量如表7所示。同时，图2给出了不同来水年下各作物实际供水量上、下限的变化趋势。根据图2可以看出，由于枯水年水量较少，石榴和核桃都没有分配水量，而红枣的实际供水量在该年需水量的区间内，平水年，石榴的实际供水量上限刚好达到石榴年需水量的下限，核桃实际供水量的上限也大于其年需水量下限，这是由于核桃种植面积比石榴大且收益值和惩罚值也大于石榴，所以在平水年给核桃和石榴供水时会优先满足核桃的需水，而一旦平水年来水量不能满足三种作物的实际供水量上限时，模型还是选择在有限情况下满足红枣的需水要求。这是因为红枣种植面积占绿洲农业总面积的59.4%，且红枣的单位收益最高且惩罚最高。丰水年，由于可用水量丰富，所以三种作物的实际供水量都达到了年需水量要求。

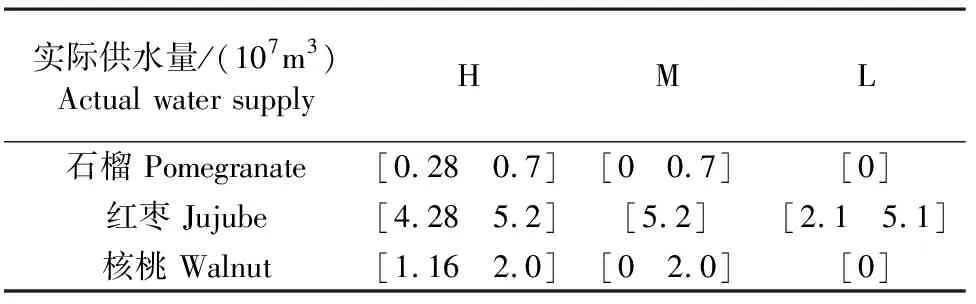
表7 不同来水年各经济果林实际供水量(λ=0.5,α=0.5)

基于以上分析，我们给出如下种植结构调整的意见：策勒绿洲红枣不仅质量好、产量高，而且个大核小果肉多，深受消费者的喜爱，且绿洲红枣已经打造出了它的品牌效应，所以，红枣种植面积可在原有基础上在考虑可用水量的情况下适当扩大；对于核桃来说，新疆干果已经有了较成熟的销售市场和加工产业链，也形成了一定的品牌效益，且随着人们更注重营养均衡和搭配，核桃市场价格不断上升，绿洲决策者可在调研市场取向后选择扩大核桃的种植面积，在有限的水资源及均衡发展绿洲生态经济的前提下适当提高GDP增长。

3 结论和讨论

本文利用区间两阶段抗风险随机规划模型对新疆和田地区策勒县的策勒绿洲中三种经济果林的最优配水方案进行了研究。该研究考虑策勒河径流对绿洲农作物的补给情况，结合概率密度函数和区间模糊特征计算并预测了丰、平、枯不同来水情景下的各作物优化配水和收益情况，确保系统收益最大化。为不同风险偏好的决策者提供了不同的方案选择。然而，策勒绿洲水资源分配是由极其复杂、高度综合的系统决定的，所以本研究在考虑绿洲特色经济果林的优化配水问题中存在着以下不足：

(1)首先，策勒绿洲的维系和发展离不开策勒河补给，但也离不开地下水的补充。本文对绿洲水资源分配系统进行了简化，只考虑策勒河径流量和三种作物需水量的不确定性以及经济参数的模糊性。在以后的研究中，需要结合地表水和地下水对策勒绿洲水分配进行综合考虑。

(2)策勒绿洲各种植区域铺设了引水渠以便为作物供水，在实际供水过程中，渠系输水会产生蒸发损失和引水损失，同时，地下水抽取还未规范化，这些实际情况都需要合理地纳入考量范围。

基于上述结论，在以后研究中，可结合地表水-地下水以及渠系输水以达到多水源多阶段的综合供水目标，使得绿洲经济发展更稳定更长远。