基于文化基因算法的隧道多回路电缆优化
2021-12-07牛海清陈泽铭颜天佑唐兴佳聂程
牛海清 陈泽铭 颜天佑 唐兴佳 聂程
(1.华南理工大学电力学院,广东 广州 510640;2.广州电力设计院,广东 广州 510610)
随着城市改造和建设不断深入,城市电网中电力电缆所占的比重越来越大[1-4]。相比于架空输电线路,地下电缆具有运行可靠、受外界环境影响小、节约输电走廊空间、不影响城市美观等优点。相比于地下电缆的直埋敷设、管道敷设、电缆沟敷设方式,隧道敷设具有巡视方便、易于故障测寻、散热条件好,载流量大等优点,成为多回路高压电缆主要的敷设方式和发展方向[5-6]。
为节约城市用地、满足城区庞大的电能需求,实际的隧道电缆工程通常为多回路集群敷设,隧道内电缆可能会出现多个电压等级和负荷电流、分段长度不同等情况,使得多回路隧道电缆的布置方式优化存在一定的难度。而目前关于多物理场耦合的计算理论和方法基本完备[7],利用有限元计算方法针对复杂敷设情况的电缆多物理场耦合建模已经十分完善,在此基础上结合智能优化算法进一步对电缆的布置方式进行优化,有利于设计人员对隧道电缆的工程设计,对于充分发挥隧道敷设的优势,保证电缆的经济安全运行具有重要意义。
目前,国内外研究学者在对于电缆的布置优化相关研究方面主要是从金属护套环流优化和载流量计算优化两方面考虑的。在关于电缆环流优化的研究方面,王永志等[8]从优化电缆金属护套感应电压的角度计算分析了单回路排管敷设电缆的不同排列方式;田金虎等[9]从改善电缆护套环流的角度计算了不同的布置方式及相序排列方式的多回同相并联电缆的护套环流,得出最优的电缆布置方式;陈科技等[10]从改善电缆金属护套环流的角度对多回路混合排列方式下的互联均匀分段和不均匀分段电缆进行计算分析。以上研究仅考虑了电缆的磁场计算和接地方式,但不涉及电缆的热场仿真及载流量计算。
在关于电缆载流量优化的研究方面,乐彦杰等[11]从提高电缆载流能力的角度对多回路排管敷设电缆进行了计算分析,但该研究不涉及电缆布置方式的优化方法。雷成华等[12]从降低电缆温度的角度,将有限元技术与粒子群优化的灵活性和有效性相结合,优化电缆间距、埋深和回填土热阻系数。鲁志伟等[13]从提高电缆载流能力的角度,基于人工鱼群算法提出电缆不等间距优化设计方法。以上研究主要从优化电缆布置位置的角度提高电缆载流量,但不涉及电缆的相序排列方式优化。
鉴于以上研究现状,本文针对典型隧道多回路电缆,建立其磁-热-流-路的多物理场耦合模型,利用COMSOL with MATLAB联合仿真计算电缆的温度、金属护套感应电压及其环流;引入文化基因算法,以电缆最高线芯温度最小化为目标函数、以金属护套感应电压不超过规范值为约束条件,对多回路电缆的布置位置和相序进行优化。
1 隧道电缆磁-热-流-路多物理场仿真模型
1.1 隧道磁-热-流-路多物理场数学模型
通常隧道敷设电缆长超过1 000 m,采用交叉互联接地方式。本文考虑严重情况,假设隧道风机未启动,隧道内空气流动形式为自然对流。由于电缆轴向尺寸远大于径向尺寸,可以采用二维模型进行仿真研究,控制方程如下。
(1)磁场控制方程
本文研究的磁场为稳态低频涡流场,相对于传导电流密度,位移电流密度较小可以忽略不计,磁场控制方程为
(1)
式中,A为矢量磁位,μ为磁导率,Js为电流密度,B为磁通密度。
(2)热场控制方程
考虑隧道内部存在热传导、热对流、热辐射的传热过程,其控制方程为
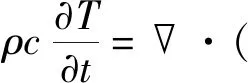
(2)
q=hΔT
(3)
(4)
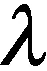
(3)流场控制方程
考虑流体力学质量守恒、动量守恒和能量守恒,控制方程分别如下:
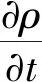
(5)
(6)
(7)
式中,cp为定压比热容,p为流场压力,η为流体动力黏度,v为流速,F为体积力。
(4)磁-热-流耦合控制方程
考虑磁场和热场之间的耦合关系以及空气流动对热传导方程式(2)的影响,磁场、热场和流场的耦合关系可由式(8)-(10)来描述,其中式(10)为能量守恒方程,从左到右分别表示内能随时间增量、热对流散热量、热传导热量、热源生成热量。
(8)
(9)

(10)
式中:J为电流密度,包含线芯电流和金属护套环流密度;Qv为单位体积电磁损耗;σ为材料电导率;α为温度系数;σref为参考电导率;Tref为参考温度。
(5)磁场耦合电路接口
电缆金属护套接地方式对环流影响很大,进而影响隧道电缆的温度场分布,因此在模型中必须考虑电缆的接地方式。工程上长电缆通常采用交叉互联的方式接地。
如图1所示,对于交叉互联位置相同的回路,需建立mf1到mf3共3个磁场模块再结合电路接口建立交叉互联接地方式下的电缆模型。图中,L1、L2、L3分别为某一个交叉互联大段三小段电缆的长度,对应mf1到mf3磁场的面外厚度;Ren为第n回路电缆的等效接地电阻。

图1 交叉互联接地模型Fig.1 Cross-bonding grounding of metallic sheath
金属护套环流计算式为
[Ish]=[Y][Ush]
(11)
式中,[Ush]和[Ish]中的元素分别对应金属护套感应电压和环流,[Y]为电路中的节点导纳矩阵,金属护套感应电压由磁场模块计算得到。
1.2 隧道磁-热-流-路多物理场的几何模型
文中选取广州地区某隧道敷设多回路电缆作为研究对象,该隧道内部实景图如图2(a)所示,隧道全长大部分采用盾构暗挖方式,共敷设7回路高压单芯电缆,其中回路Ⅰ~Ⅳ(110 kV)和回路Ⅴ~Ⅶ(220 kV)电缆型号分别为YJLW02-64/110 1×1 200 mm2和YJLW02-127/220 1×2 000 mm2,各回路电缆以“品”字型接触排列。回路Ⅲ、Ⅳ、Ⅴ、Ⅵ电缆支架长度为700 mm,回路Ⅰ、Ⅱ、Ⅶ支架长度约为500 mm。本文根据各回路电缆到隧道壁的最短距离定义回路电缆在电缆支架上的位置,经测量回路Ⅰ~Ⅶ电缆位置分别为:315、205、269.9、478、229、294.6、160 mm,隧道断面如图2(b)所示。在此断面基础上,考虑到周围土壤的环境影响,本文建立18 m×15 m的几何模型。

图2 七回路隧道敷设电缆(单位:m)Fig.2 Seven-circuit cable laying in tunnel(Unit:m)
1.3 隧道磁-热-流-路多物理场的边界条件
根据本文模型中添加的4个物理场接口,边界条件设置如下:
(1)磁场模块。在各回路电缆的线芯施加电流激励,分别对应各回路电缆的负荷电流。
(2)热场模块。模型的下边界设置温度为深层土壤温度;左右边界设置为热绝缘;上边界设置为地面外部自然对流,传热系数为空气自然对流传热系数。相关参数都根据实测数据进行设置。
(3)流场模块。隧道墙和电缆表面设置为壁边界条件,体积力为重力。
(4)电路模块。根据图1所示的交叉互联接地模型进行磁路耦合,并添加电阻和接地节点形成完整的电路回路。
文中采用自动网格剖分模式,其中流-固边界采用边界层网格剖分,其他区域为三角形网格剖分,模型计算自由度数约为150万。根据1.1小节建立的数学模型,文中采用分离式求解器进行求解。分离式求解器是一种将多物理场方程组分离以采用不同求解设置的方法,适用于处理较为复杂的多物理场仿真。在本文设置的分离式求解器中,分离步1用于在频域求解磁路耦合方程组,计算电磁损耗,分离步2基于电磁损耗求解稳态热流耦合方程组,计算的温度结果用于修正电磁损耗重新计算分离步1,通过循环迭代的方式进行求解。
1.4 COMSOL with Matlab联合仿真
本文利用COMSOL with Matlab联合仿真实现对有限元模型的进一步优化研究。具体实现过程如下:
(1)建立多回路隧道敷设电缆有限元模型,通过参数化建模,将相序和位置变量定义为可变的输入参数,设置探针在后处理中输出温度和感应电压计算值,即输入—模型—输出的形式。
(2)将有限元模型以“ModelClient”形式加载到Matlab的工作区间,对模型输入参数进行赋值,能够调用工作区间的有限元模型并输出计算结果。
(3)在Matlab中编写程序,利用文化基因算法对优化变量进行寻优搜索,实现对目标函数的优化。
2 隧道电缆相序及位置优化的文化基因算法
2.1 优化目标及约束条件
载流量是电缆设计和运行中的一个重要参数,为保证电缆的经济安全运行,设计人员通常考虑电缆载流量在一定条件下的最大化。电缆的额定载流量是指电缆绝缘层温度(与线芯相接触)达到其材料长期工作的最高允许温度所对应的最大负荷电流[14],即电缆的载流量由电缆群的最大线芯温度决定,载流量的最大化等价于一定负荷电流下电缆线芯温度最大值的最小化。因此本文研究的目标函数为电缆在一定负荷电流下,线芯温度的最大值。
根据GB50217—2018《电力工程电缆设计规范》,高压交流单芯电缆设有安全装置时感应电压幅值不得超过300 V,因此根据本文的研究对象,优化的约束条件为电缆金属护套感应电压的最大值不超过300 V。
当隧道敷设电缆负荷电流一定时,电缆线芯的温度与电缆相序和电缆的排放位置有关,优化回路电缆相序组合和电缆位置可以降低电缆的金属护套环流及其发热损耗,削弱回路电缆之间的互热效应,降低隧道电缆温度。因此本文考虑以各回路电缆的相序和水平位置两种变量对隧道电缆的布置方式进行优化。
隧道敷设电缆示意图如图3所示,图中li为第i回路电缆的水平位置变量(假设该回路电缆线路所放支架位置确定),表示第i回路电缆到隧道壁的最短距离值,单位mm;ai为第i回路电缆的相序变量,通过定义函数映射,其取值可分别对应第i回路三相电缆可能的6种相序排列情况,即ai∈{1,2,3,4,5,6},分别对应图3中电缆1-2-3的相序分别为C-A-B、C-B-A、A-C-B、A-B-C、B-A-C、B-C-A。

图3 隧道电缆的位置变量Fig.3 Position variable of cable laying in tunnel
因此该优化问题可由式(12)描述:
minTmax(X)
(12)
s.t.X=[a1,a2,…,an,l1,l2,…,ln],
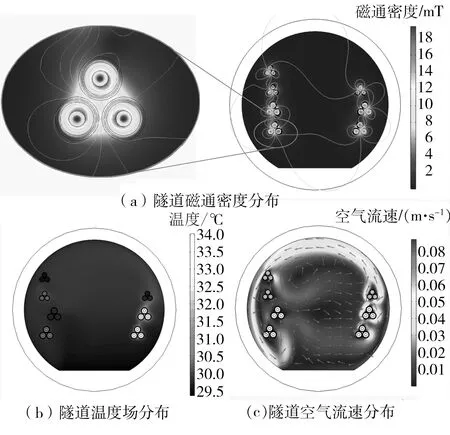
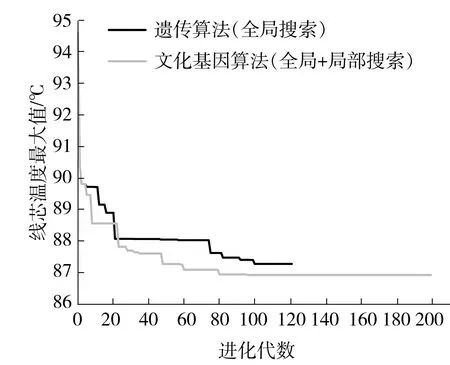
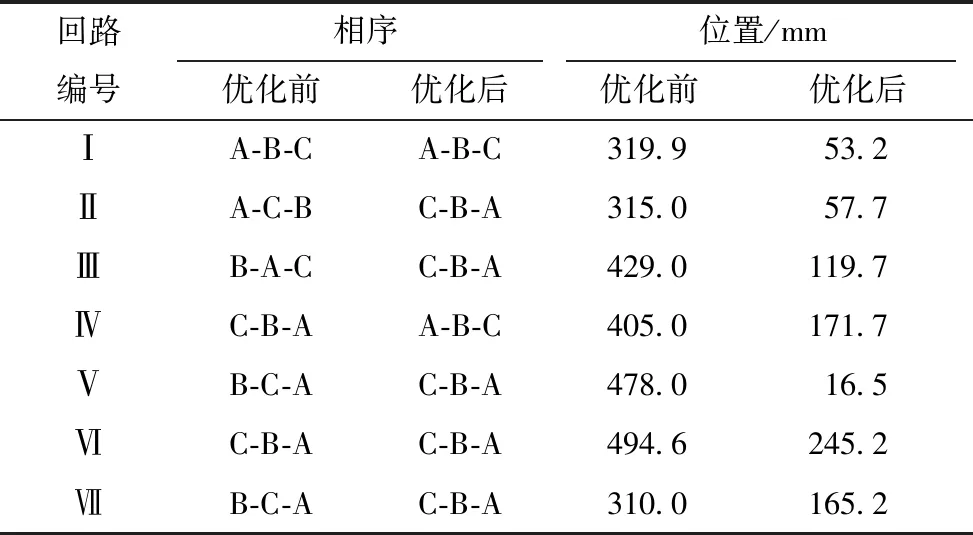
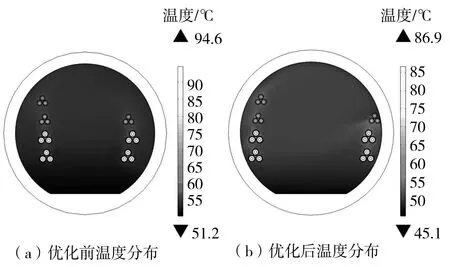
Ush(X) l1,l2,…,ln∈Ω1, a1,a2,…,an∈Ωa。 式中:n为隧道电缆的回路数;X为该问题的决策变量,包含n个相序变量值和n个位置变量值;Tmax和Ush分别为有限元模型计算的电缆线芯温度的最大值和电缆金属护套感应电压的最大值,与决策变量X有关;Ud为工程设计上允许的电缆金属护套感应电压值;Ωa为相序变量的范围;Ωl为工程上允许的回路电缆位置的范围,与电缆支架长度以及电缆整体外径等因素有关。 2.2.1 优化算法的选取 由于隧道敷设电缆回路数较多,模型中涉及到电磁场、电路、温度场以及流场等多个物理场的直接耦合,其几何和数学模型较为复杂;优化变量较多。对于相序变量,n回路电缆共有6n种相序情况,而位置变量是连续变量,即本文所研究的优化问题包含组合优化和连续优化问题,具有较高的计算复杂度。简单的优化算法难以完成本文复杂的优化问题,因此采用文化基因算法进行优化。 文化基因算法(Memetic Algorithm)是一种基于模拟文化进化的混合全局启发式搜索算法,其算法框架与操作流程类似于遗传算法,区别在于文化基因算法在遗传算法的基础上通过引入局部搜索技术使每次迭代的个体达到局部邻域最优[15]。该方法兼备群体智能计算方法和局部搜索技术的优点,能够快速获得高质量解,具有较高的收敛性能,适用于本文所研究的问题。 2.2.2 基于遗传算法的全局搜索机制 本文选取的全局搜索算法为基于精英保留模式的遗传算法,即对种群个体进行适应值排序筛选出精英个体,而精英个体不参与遗传进化过程,具体实现过程如下: (1)双染色体编码与适应值函数 在本文的优化模型中,采用双染色体编码模式,相序变量和位置变量分别以位串编码和实数编码的方式编码于相序染色体和位置染色体,即染色体编码总长度为电缆回路数目的2倍。以双回路电缆为例,个体[2,3,200,100]表示双回路电缆相序分别为C-B-A、A-C-B,距离隧道壁的距离分别为200 mm和100 mm。 由于遗传算法的目标通常为种群个体适应值最大,故本文适应值函数选为电缆线芯温度最大值的负数,第j个个体的适应值为fj=-Tmax(Xj),该适应值是通过COMSOL with Matlab联合仿真调用有限元模型计算的。 (2)遗传算子 遗传算法的步骤包括选择、变异、交叉,具体实现过程分别如下:采用轮盘赌选择策略,由每个个体的适应值计算其保留到子代的概率,随机选择个体构成子代种群;采用单点交叉策略,根据交叉概率将种群中的两个体随机地交换部分染色体,能够产生新的染色体个体;采用单点变异策略,根据变异概率随机选取变异个体及其变异基因位,通过随机变异代替原有的基因,产生新的染色体个体。参考一般遗传算法参数的设置范围,本文采用的交叉概率为0.85,变异概率为0.1[16]。 2.2.3 基于小生境的自适应局部搜索机制 局部搜索中种群适应值较好的个体称为智能体(agent),文献[17]中提出一种仅对适应值优于阈值的智能体进行局部搜索的策略,通过相关实验设定阈值为0.6,即适应值为前40%的个体为智能体。 本文通过适应值大小对种群进行排序,并截取适应值较好的个体作为智能体。在此基础上提出基于小生境技术的邻域确定方法,根据智能体的稀疏度,自适应地调整其局部搜索邻域范围。 小生境技术中第k代种群Pk中个体j和r的欧氏距离定义如下[18]: (13) 稀疏距离定义为智能体j到其他所有个体的最短欧式距离: (14) 智能体j的稀疏度定义为归一化到[0,1]的稀疏距离,即: (15) 式中,Np和Na分别为种群数量和智能体数量。 在邻域搜索半径内随机生成数个子代智能体种群Ok,各智能体的邻域搜索半径和子代种群规模分别为 ragentj=sj×rj (16) Np,agentj=sj×Npj (17) 2.2.4 电缆相序位置优化的文化基因算法流程 本文基于Lamarckian模式(由局部搜索改进得到的个体将参与进化操作)[19],使用邻域局部搜索策略。首先依据原种群Pk个体适应值(即电缆线芯温度最大值的负数)分布推选智能体,各智能体在邻域半径内随机搜索形成智能体子代种群Ok,智能体子代种群与原种群混合重新选出较优秀的个体更新种群,保持局部搜索前后种群数目不变,即Pk=U(Pk×Ok)。算法流程图如下: 图4 优化算法流程图Fig.4 Flow chart of optimization algorithm 文中根据图2所示隧道电缆于2019年02月28日某平稳时刻负荷电流数据对有限元模型进行仿真并验证,隧道电流数据如表1所示。 表1 各回路电缆运行时的负荷电流Table 1 Load current of each circuit cable during operation 该隧道电缆所有回路的布置相序均为A-B-C,仿真结果如图5所示。为验证仿真模型对于电缆温度计算的准确性,本文通过红外测温试验测量电缆外皮温度,并根据IEC-60287标准利用电缆外皮温度反演计算电缆线芯温度,计算式见式(18)[20]。 图5 磁场、热场和流场仿真结果Fig.5 Simulation results of magnetic and thermal and fluid fields (18) 式中,θc和θ0为分别为电缆线芯温度和外皮温度;Td、Ts、Tw分别表示绝缘层、金属护套层和外护层的热阻;Wc、Wd、Ws分别表示导体、绝缘层、金属护套层的损耗。 图6为测温相仿真结果与测温及反演计算结果的对比,电缆外皮温度的仿真值与测量值偏差低于0.5 ℃;线芯温度的仿真值与反演值偏差低于2 ℃,模型计算误差在合理范围内,因此可以验证本文所建立的多回路隧道敷设电缆磁-热-流-路多物理场仿真模型温度场计算的正确性。 图6 仿真结果与测温及反演计算结果的对比Fig.6 Comparison between simulation results and temperature measurement and inversion results 本文设定该隧道电缆运行工况和优化变量范围如表2所示,其中对于位置变量范围,考虑有限元模型计算中网格剖分精度的要求,各回路位置变量最小值设置为15 mm,而各位置变量的最大值则是根据回路电缆整体外径和电缆支架长度所设置。 表2 电缆运行工况与优化变量范围Table 2 Operating conditions of cables and range of optimal variables 为分析隧道敷设电缆相序和位置对于电缆线芯温度最大值的影响,本文针对等相序/位置布置模式进行分析,即保持各回路的相序变量和位置变量相同,对所有相序布置情况和位置布置范围进行多物理场仿真,计算隧道电缆群的线芯温度最大值,计算结果如图7所示。 从图7可见,对于布置位置而言,存在多个局部最优点,但是全局最优点出现在位置变量取最小时,总体趋势为位置变量越小,电缆线芯温度越低,即增大隧道电缆回路的水平间距,有利于降低电缆温度。 图7 电缆线芯温度Fig.7 Cable core temperature 对于布置相序而言,由于相序旋转的对称性,相序1、4、6是等效的,均为顺时针正序排列,环流损耗相同,因此温度计算结果相同,相序2、3、5之间也是类似,为逆时针负序排列,因此投影到位置-温度面上,只有正序和负序两种情况。位置变量处于[50 mm,100 mm]区间时,负序排列优于正序排列,而当处于其他区间时,正序排列优于负序排列。在实际电缆工程设计中,应当根据各回路电缆所处的位置,以降低环流损耗和线芯温度为目标选择合适的电缆回路相序布置方式。 当各回路电缆的相序和位置不等布置时,本文选择一种较为恶劣的相序位置布置方式(即回路水平间距较小、相序组合对应的环流损耗较大),采用文化基因算法进行电缆相序和位置的联合优化。考虑本文所研究的隧道敷设电缆回路数为7,即相序染色体和位置染色体长度均为7,设置每代的种群数目为20,种群最大进化代数为200代。迭代过程中收敛曲线如图8所示。 从图8可见,针对该优化问题,相对于全局搜索遗传算法,在文化基因算法全局和局部的双重搜索机制下,对于目标函数的优化效率更高。在进化迭代代数进行到第100代以后,电缆线芯温度已保持稳定,可以认为该布置方式对应的次优解已接近该优化问题的最优解。 图8 算法收敛情况Fig.8 Algorithm convergence situation 表3为优化前后的隧道电缆布置方式,表4为优化前后的整体电缆参数对比。经优化后,电缆的最高线芯温度下降了8.18%,金属护套感应电压下降了21.39%,金属护套总环流损耗下降了30.62%,环流平均值下降了8.20%,从整体上改善了隧道电缆的布置方式。 表3 优化前后的隧道布置方式Table 3 Tunnel layout before and after optimization 表4 优化前后的电缆参数Table 4 Cable parameters before and after optimization 图9为优化前后各回路电缆参数对比,图10为优化前后的隧道温度场分布。回路Ⅰ-Ⅳ(220 kV)电缆线芯温度和护套环流损耗平均分别下降了8.19 ℃和18.64 W/m;回路Ⅴ-Ⅶ(110 kV)电缆线芯温度和护套环流损耗平均分别下降了6.44 ℃和8.22 W/m,220 kV电缆的优化效果优于110 kV电缆。经优化后的隧道温度从整体分布上均有所改善。 图9 优化前后的参数对比Fig.9 Comparison of parameters before and after optimization 图10 优化前后的温度分布Fig.10 Temperature distribution before and after optimization 优化结果表明,经优化后,电缆温度均有所降低,回路水平距离增大,电缆布置位置有明显贴近隧道壁的趋势,各回路电缆环流损耗明显下降。一方面,通过增大电缆回路之间的水平距离有利于削弱回路电缆之间的互热效应,改善电缆散热;另一方面通过选择合适的相序组合方式可以大幅度地降低金属护套环流,从而减少电缆发热。同时当隧道中存在多个电压等级电缆时,对于相序优化优先考虑削弱承担较大负荷电流的高电压等级电缆环流,有利于进一步降低隧道电缆发热。 本文研究表明,采用文化基因算法,选择优化后的位置和相序布置方式有利于削弱回路电缆之间的互热效应,降低金属护套环流发热损耗,改善隧道电缆的布置方式。 本文以多回路隧道敷设电缆为研究对象,考虑其电磁场、热场、流场以及金属护套的交叉互联的接地方式,针对广州地区某隧道七回路电缆建立了磁-热-流-路耦合的多物理场有限元仿真模型,并通过红外测温实验验证了有限元模型温度场计算的正确性。然后通过给定电缆线芯电流,以隧道各回路的电缆相序和水平位置作为优化变量,以金属护套感应电压不超过工程规范值为约束条件,以电缆最高线芯温度最低为目标函数,选择一种较为恶劣的布置方式,引入文化基因算法进行布置方式优化。优化后电缆的最高线芯温度、护套环流损耗、环流平均值、感应电压分别下降了8.18%、21.39%、30.62%、8.20%。 优化结果表明,采用文化基因算法,选择优化后的位置和相序布置方式有利于削弱回路电缆之间的互热效应,降低金属护套环流发热损耗,改善隧道电缆的布置方式。对于在隧道电缆工程设计中提升电缆载流能力,充分发挥隧道敷设优势,保证电缆的经济安全运行具有重要意义。2.2 文化基因优化算法及其优化流程
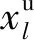
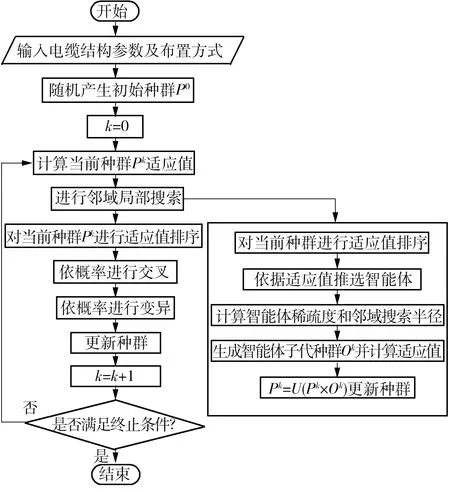
3 基于测温的隧道电缆温度场计算模型验证


4 隧道电缆位置相序联合优化分析

4.1 电缆等相序/位置布置模式分析

4.2 基于文化基因算法的电缆相序位置联合优化


5 结论
