空间飞行器界面力限控制技术研究

庞家志，魏伟，李旭，孙佳川，李枫

（1.航天科工防御技术研究试验中心，北京 100854；2.空军装备部驻北京地区第四军事代表室， 北京 100041；3.航天科工空间工程发展有限公司，北京 100854）

航天器产品在全寿命周期中需经受复杂的力学环境，通常会给产品带来不同程度的机械损伤与功能下降。如紧固件松动、密封失效、电容和介电常数变化等[1]。因此为检验产品是否能够正常运行，需要对产品进行充足的试验。

在航天器振动试验中，通常通过控制振动台与产品之间的加速度量级来完成对产品的考核。然而在制定振动加速度试验条件时，需要对数据进行包络与平滑处理。同时，振动过程中存在动力吸振效应，所以在这种振动加速度试验条件下可能会引起严重的过试验。

与传统的加速度控制方法相比，力限试验技术是加速度与力双重控制试验方法。其中加速度是主动控制，在界面力不超过力限条件时，按振动加速度试验条件进行；当界面力超过所设定限制条件时，力响应控制迫使加速度控制条件下凹，从而有效避免过试验的发生，进而对航天器施加更加合理的力学环境考核。

20世纪50年代，有关专家提出了多点控制降低结构共振的影响与力限控制技术，解决共振频率的过试验问题[2-4]。1997年，Scharton[5]将多年力限试验成果整理为《力限振动试验专论》。2000年欧空局ESTEC利用力测量装置FMD开展了ROSETTA卫星结构星及飞行星的力限控制振动试验，取得了较好效果。2004年，加拿大空间局通过模型进行了力限控制试验研究，确定了力限半经验法的使用范围。2017年，NASA联合多家实验室利用力限控制技术对LEOStar-2/750小卫星及ICON Observatory天文望远镜开展了振动试验，取得了非常成功的试验效果。

我国关于力限试验的研究起步较晚。于海昌[6]、金询叔[7-8]和王晓耕[9]等介绍了航天器振动试验的情况。近年来，国内力限试验技术开始逐步发展。于新战等[10]阐述了振动试验中动力吸振的机理。张俊刚等[11]回顾了解决过试验的方法。沈凤霞[12]介绍了力限振动试验中传感器的类型、使用安装及测量技术。李新明等[13]以某试件承力筒进行了力限振动试验。周莹等[14]通过数值仿真算例，验证了测量和控制界面加速度和界面力，可以明显地减轻过试验的程度。王珂晟等[15]介绍了力限技术应用的关键技术问题并对存在的难点开展分析。岳志勇等[16-18]探讨了在我国航天器振动试验中应用力限控制方法面临的问题及可能的解决方法。李腾飞[19]对用于估算界面力的模型进行了简化。张相盟[20]设计铝板结构进行力限试验，证明方法的有效性。张群等[21]提出一种基于振动台电压电流的界面力监测方法,建立界面力的获取程序和基于界面力评估的加速度振动控制方法。朱仪凡等[22]给出了一种基于振动台电枢测力法在航天器振动试验中的应用方法,验证了基于振动台电枢测力法的合理有效性。从目前实际发展情况看，力限控制技术在国内仍处于起步阶段，由于试验技术及试验成本等多方面的限制，力限控制技术仍未得到广泛推广与应用。

本研究以空间飞行器模拟件为试品，以力限控制原理模型为依据，通过搭建力限控制振动系统，获取力限参数，并在此基础上，以极小包络法建立力限控制方程，开展了力限控制试验，研究了力限控制技术的有效性及技术特点。

1 研究模型

1.1 力限控制原理模型

力限控制技术是以加速度控制为主，以力限控制为辅。在正弦扫描试验中，当响应控制点未达到力限值时，控制输入按振动加速度试验条件；当结构共振响应控制点达到或超过力限值时，控制系统自动实现控制通道的转换，按力限控制；当共振峰过后，随着响应控制点量级的下降，控制系统又转回加速度控制通道。在随机振动试验中，在共振频带以外，加速度控制起作用；在共振频带以内，由于力响应的限制，使加速度输入条件下凹。力限控制原理模型如图1所示。

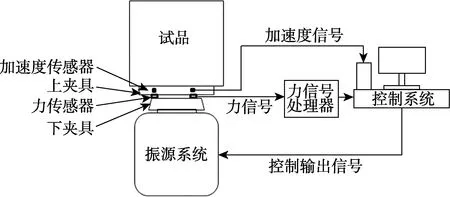
图1 力限控制原理模型 Fig.1 Force limit control principle model

1.2 试验组成模型

通过试验夹具将试品与力传感器及振动台连接，4个力传感器均布安装在试验件与振动台之间，并施加预紧力。试验前，采用低量级正弦扫频的方式对力传感器进行动态力校准。试验时，力传感器测量到的力信号通过处理器计算后，传递至振动控制系统，实现对试验系统动态力信号的准确采集。同时，在振动台与试品的界面连接处安装加速度传感器，实现对试验系统的加速度控制。加速度测量点位于试品顶部上表面中心位置，用以监测产品的共振响应信号。

2 力限双控方程建立

力限振动试验同时需要加速度谱和力谱，采用包络的方法制定力限谱，即首先采用简单二自由度法、复杂二自由度法、半经验法分别计算界面力限试验条件，然后对得到的结果进行包络，得到最终力限试验条件。

2.1 力限参数获取

建立力限控制方程，首先应确定力限参数。在力限控制方程中，涉及到的主要力限参数包括视在质量、有效质量及残余质量。

视在质量：指线性定常系统中结构某一点的激励力与相应的加速度之比。在耦合系统的界面处，界面力是界面加速度与视在质量的乘积。

有效质量：振动系统中每阶模态下单自由度振子的质量。在并联的振动单元中，振动单元与一个共同的刚性无质量基础相连，每一个振动单元都代表了实际结构的一个振动模态，其质量为相应的模态质量。对任意一个模态来说，有效质量大小的定义是，使质量块与刚性基础之间的响应力与实际结构在此模态下振动时底部的响应力相等。对每个振动方向来说，所有模态的有效质量之和等于结构的总质量。

残余质量：激励频率以上结构谐振频率所对应的有效质量之和，即产品质量减去激励频率以下所有谐振频率所对应模态的有效质量。

通过低量级正弦扫频试验的方法[23]，得到振源及试品的力限参数测定结果，见表1及表2。该试验中，振源实际总质量为153.8 kg，负载实际总质量为115.5 kg。由表1和表2可知，振源及负载所取前几阶模态对应的有效质量之和已接近振源及负载的实际总质量，因此忽略其他次要模态频率。

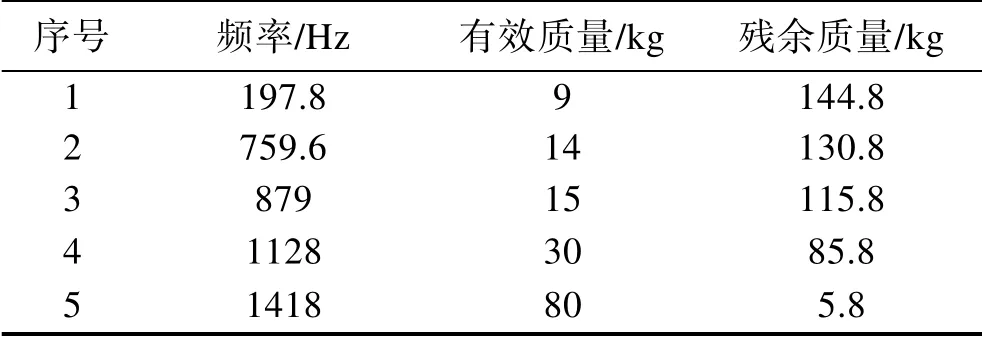
表1 振源激励前5阶固有频率及其有效质量 Tab.1 The preceding 5 models frequency of the vibration source and its effective mass

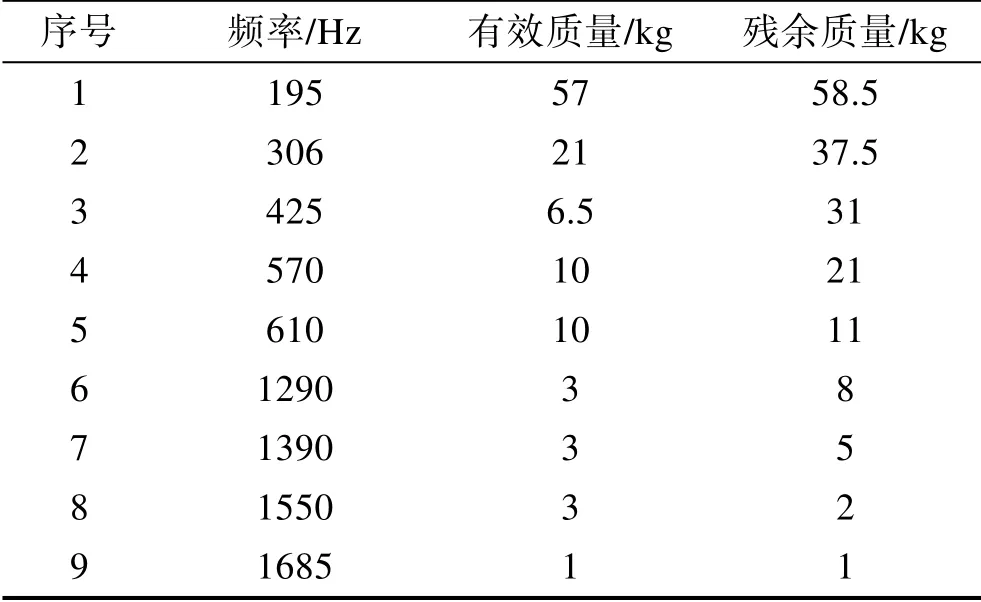
表2 负载前9阶固有频率及其有效质量 Tab.2 The preceding 9 models frequency of the load and its effective mass

2.2 力限控制方程建立

力限谱主要有两种确定方法，一种是结合实践确定的半经验法，另一种是耦合系统分析方法。其中耦合系统分析方法针对支撑系统和负载系统进行耦合分析，耦合系统分析方法又可分为简单二自由度法和复杂二自由度法。

本研究中，首先利用半经验法、简单二自由度法及复杂二自由度法分别建立力限控制方程[5]，然后再以不同力限控制方程进行最小包络，建立最终力限控制方程。

2.2.1 半经验法

半经验法是以一种简单的方式制定力限谱，半经验法中的力限谱在每一个频点上与加速度谱成正比。当飞行试验中测得的力和加速度的峰值存在明显不同的频点时，力限谱应根据实际情况调整。

在正弦振动试验中，力值F与加速度值A的力控方程为：

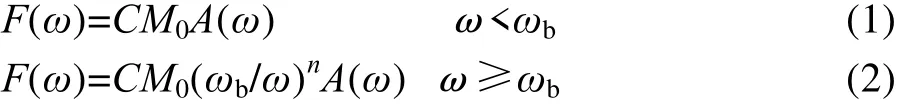
式中：C为无量纲经验常数；M0为试品总质量；ω为频率；ωb为拐点频率，通常定义为试品在小量级振动中的一阶共振频率，也可通过模态试验或有限元分析获得；n为正常数，一般为1～3，通常取1，其值可通过小量级振动试验进行估计。

在随机振动试验中，力限方程为：

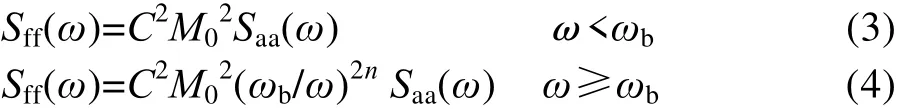
式中：Saa为输入加速度功率谱密度；Sff为界面力功率谱密度。

在工程实践中，C值可通过简单或复杂二自由度法、有限元法或从飞行测试、地面测试及查阅相关文献等方式获得。本研究中，C值取3.4。

半经验法公式简单、易操作，基于地面振动数据即可得到力限方程，具有很大的应用优势。但该方法要求工程技术人员具有丰富的工程实践经验，并且需要足够多的相似结构飞行遥测数据及地面力限振动试验数据的积累。

2.2.2 耦合系统方法

耦合系统方法分析流程如下：将欲分析的频段划分为若干频段（一般按1/3倍频程带宽）；选择第一个（或下一个）频带；建立相应频带内由支撑系统和负载系统组成的耦合系统等效模型；计算该频带内耦合系统模型各个参数（一般由视在质量、有效质量、残余质量、模态阻尼等组成）；计算该频段内支撑系统和负载系统在界面处的最大界面力与最大界面加速度比值的最大值；以加速度试验谱乘以上述比值，获得该频段内的界面力试验条件；按上述步骤计算其他剩余频段的界面力试验条件；得到整个频率范围内的界面力试验条件（力限谱）。

2.2.2.1 简单二自由度法

简单二自由度法的基本模型如图2所示。该模型中，源（支撑系统）的振动模型与负载的振动模型相互耦合，源与负载的质量简化为一个质量。模型中源与负载的质量为残余质量，忽略了有效质量。

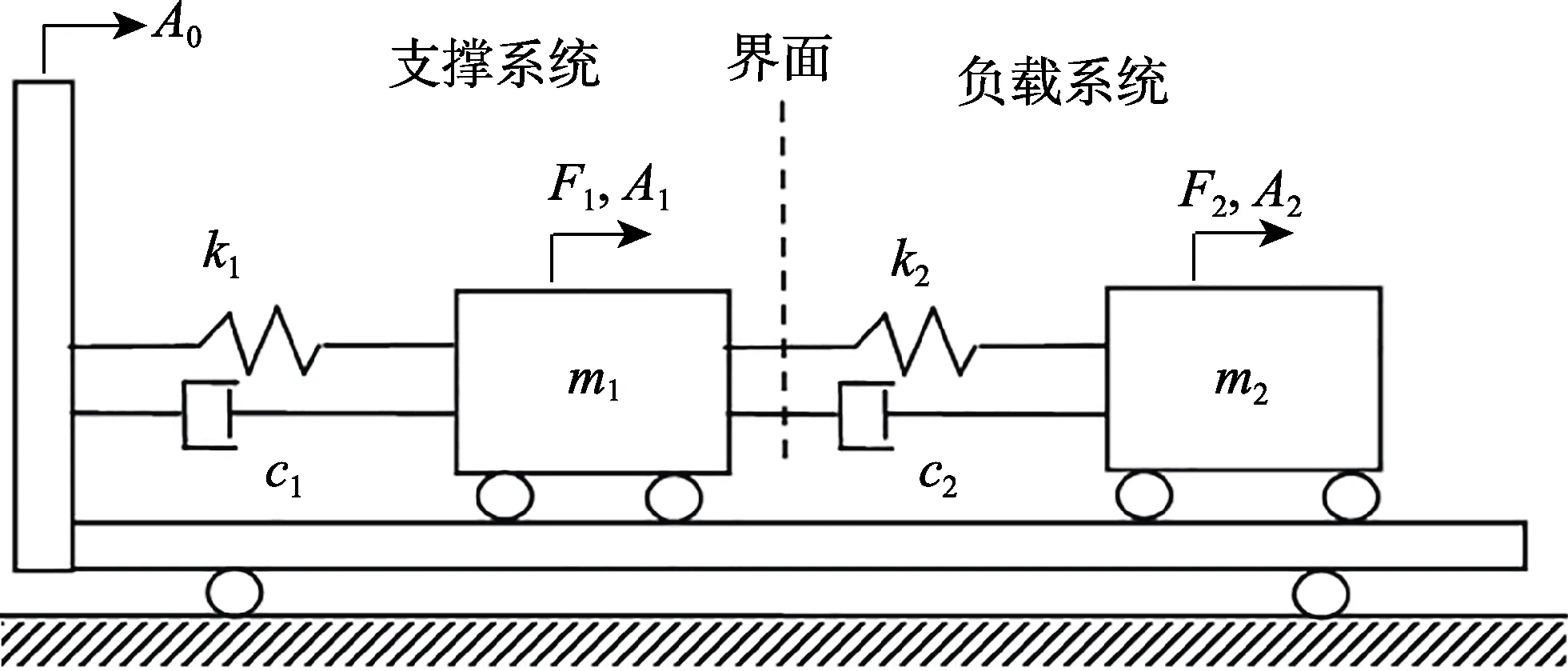
图2 简单二自由度耦合振动模型 Fig.2 Simple two-degree-of-freedom system of coupled oscillators

在简谐激励和随机激励作用下，力限条件为耦合系统界面力最大值，即：

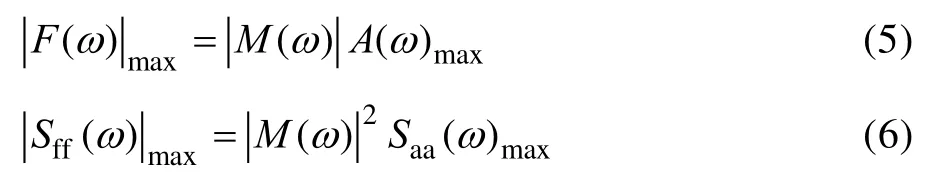
式中：F(ω)为耦合系统界面力；A(ω)为耦合系统界面加速度；M(ω)为耦合系统负载视在质量。

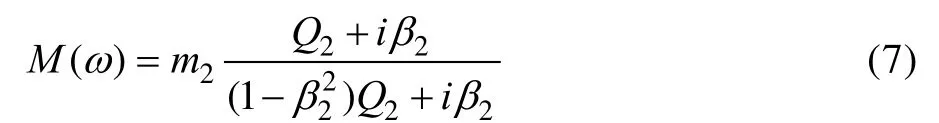
式中：Q2为负载共振时的放大系数，Q2=1/(2ξ2)；ξ2为负载系统阻尼比，ξ2=c2/(2(k2m2)0.5)；β2为界面力最大时的共振频率。

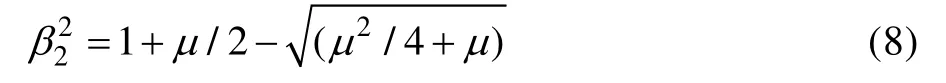
其中，μ=m2/m1。

定义γ为力限条件归一化系数为：

由此确定随机振动力限条件为：

正弦振动力限条件为：

简单二自由度法考虑了放大系数Q2以及源和负载残余质量之比μ两种因素，计算方法相对简单。但由于该方法将源和负载分别简化为一个弹簧阻尼质量系统，不能全面地反应结构的动力学特性。

2.2.2.2 复杂二自由度法

复杂二自由度系统振源系统和负载系统组成的耦合系统可等效为图3模型。其中M1和m1分别为激振频段内支撑系统的残余质量和有效质量；M2和m2分别为激振频段内负载振子的残余质量和有效质量；c1和c2分别为激振频段内的两个系统的模态阻尼；k1和k2分别为激振频段内两个系统的模态刚度。复杂二自由度模型中，支撑系统和负载系统分别使用2个质量单元表示系统的有效质量和残余质量。该模型综合考虑了系统的共振模态和非共振模态对界面力的贡献。

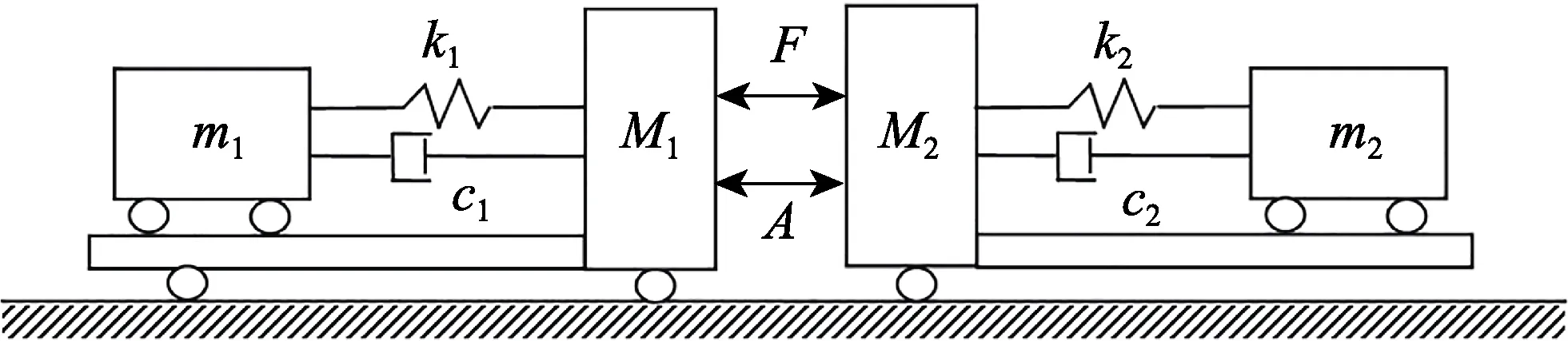
图3 复杂二自由度耦合振动模型 Fig.3 Complex two-degree-of-freedom system of coupled oscillators

复杂二自由度耦合系统无阻尼共振频率为：

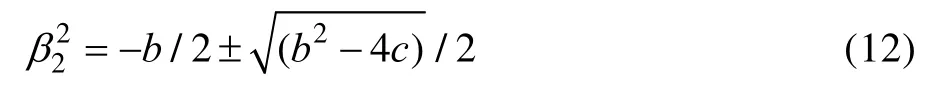
其中：

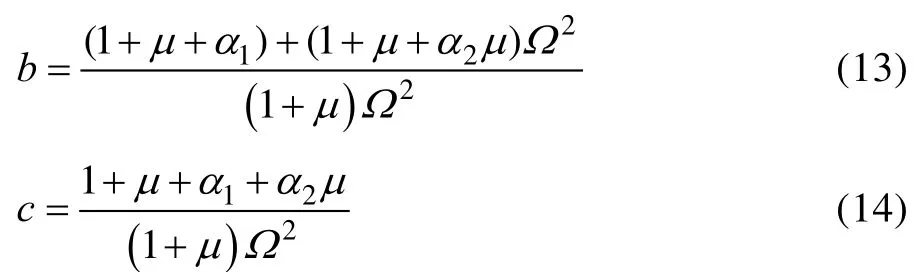
式中：μ=M2/M1，α1=m1/M1，α2=m2/M2，Ω=ω2/ω1，ω1=(k1/m1)0.5，ω2=(k2/m2)0.5。

界面处负载的表观质量为：

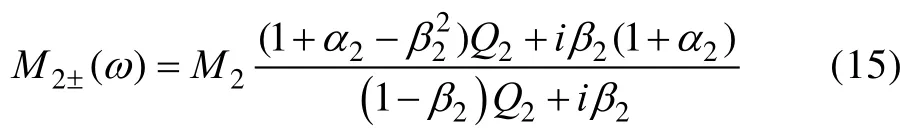
源的表观质量为：

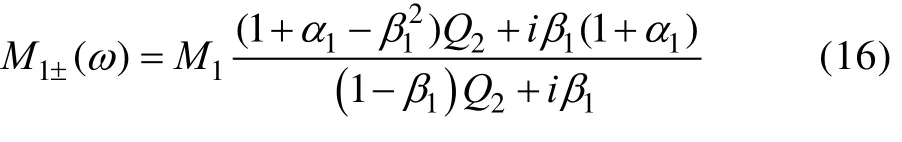
其中，β1=ω/ω1，为二自由度耦合固有频率与源非耦合固有频率比。

对于任何激励，源与负载系统的界面加速度A与自由加速度A0（源无负载时）之比为：

A0与外激励F间的关系表达式为：

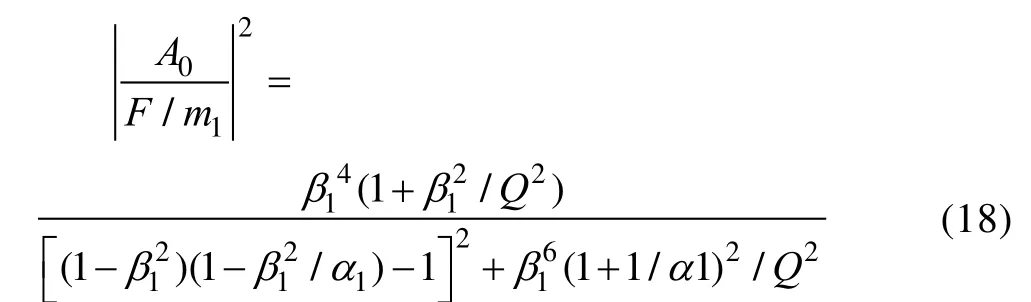
通过式（17）、（18）可计算得到界面加速度A。 对于简单二自由度模型，界面加速度峰值和界面力峰值通常在系统共振频率上出现；对于复杂二自由度模型，界面加速度峰值和界面力峰值可能不在同一个共振频率上出现。当外力激励为定值，且源与负载质量相当时，得出的力限条件最为保守。表3给出了界面加速度和界面力最大值出现的可能位置及其比值。

表3 Amax、Fmax出现的可能位置及其比值 Tab.3 Possible locations and ratios of Amax and Fmax

定义γ为复杂二自由度力限条件归一化系数：

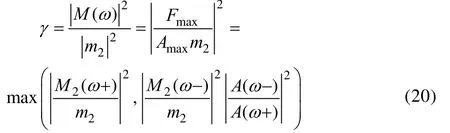
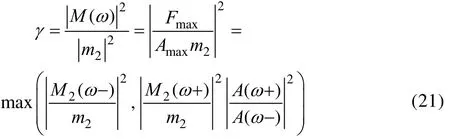
通过改变协调参数Ω值，可以得到不同协调参数下界面力谱峰值和界面加速度谱峰值比值的最大值（即（|Fmax/Amax|max）。在协调分析过程中，协调参数的平方一般为从0.5增加到2，步长为1/16。

由此得到随机振动力限条件为：

正弦振动力限条件为：

复杂二自由度法计算模型同时考虑了源和负载的有效质量和残余质量，比简单二自由度法更能反映结构特征。因此制作的力限条件相对精细，但复杂二自由度法操作程序复杂，不便于在实际中应用。

2.2.3 力限控制方程的建立

试品原始输入随机振动条件Saa为：20～1000 Hz，0.04g2/Hz；1000～2000 Hz，–6 dB/Oct。根据2.1节得出的力限参数，采用不同力限控制方程获得的力限控制谱如图4所示。

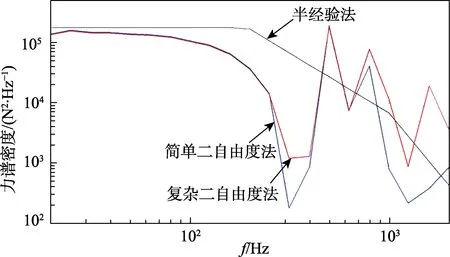
图4 不同力限控制方程计算得到的力限控制谱 Fig.4 The control spectra calculated by different force-limit methods

利用上述所得的半经验法、简单二自由度法及复杂二自由度法建立的不同力限控制谱，对图4中每个频率点下对应的的力谱密度值（纵坐标）分别取最大值及最小值，得到力限控制谱的最大包络谱及最小包络谱如图5所示。

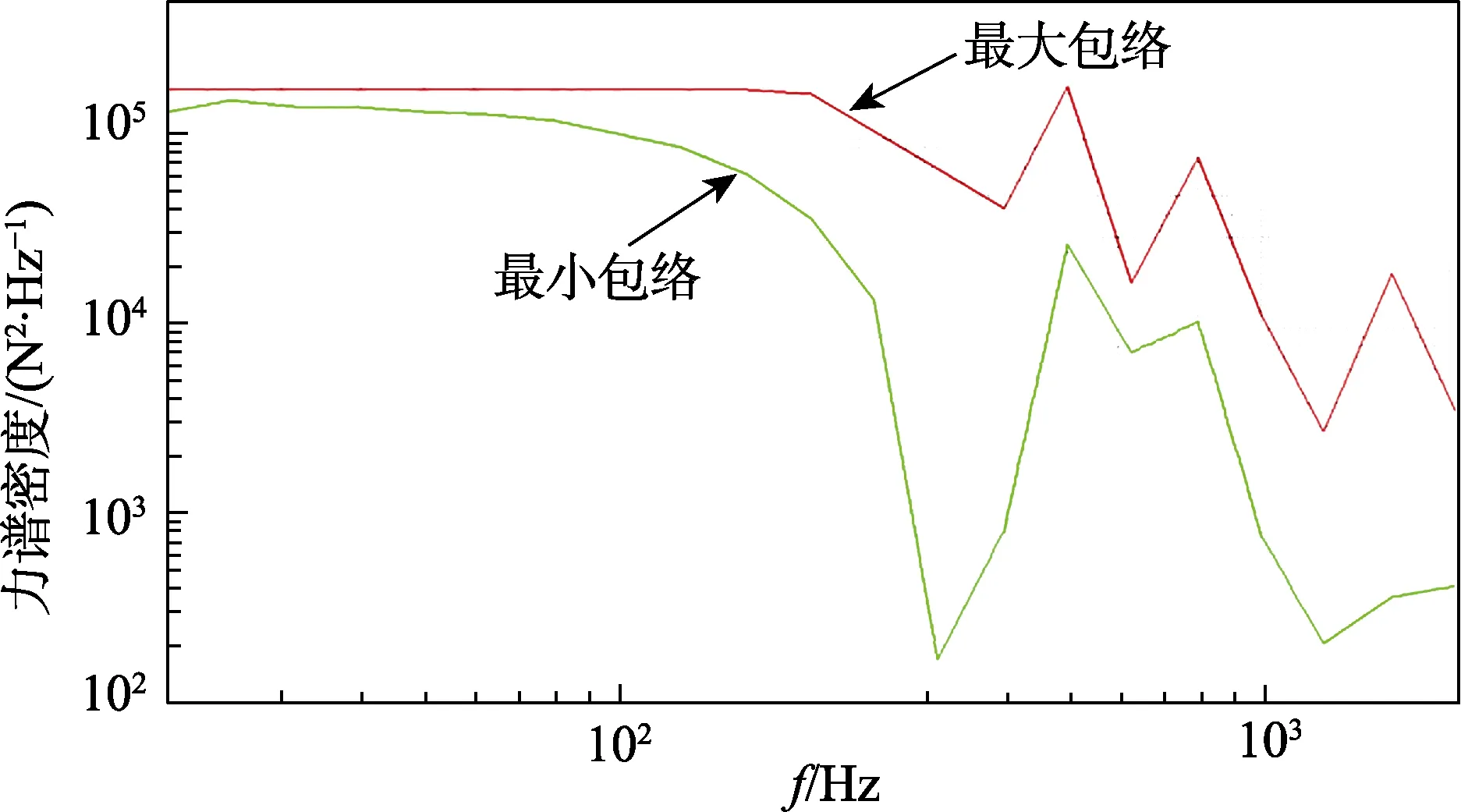
图5 力限控制谱最大及最小包络 Fig.5 The maximum and minimum envelope of the force limit control spectrum

3 试验分析

分别以无限制、加速度限制及力限三种控制方法对试品开展试验，通过加速度控制曲线、测点加速度响应曲线及力值曲线分析力限控制效果。无限制、加速度限制及最小包络力限控制时的随机振动控制图谱见图6。

由图6可知，在无限制及加速度限制下，控制图谱在400 Hz左右存在明显的峰值，且高频处控制曲线波动较大，控制极不稳定。在加速度限制下，相对于无限制情况，虽然控制曲线呈现了一定的被抑制现象，但并没有针对试品共振响应频点处进行抑制。从力限控制曲线可以看出，在力限作用下，振动曲线整体控制比较稳定，且在预期的共振频带处呈现倒三角下凹现象，下凹峭度比较大，对共振频带处的抑制比较精准。

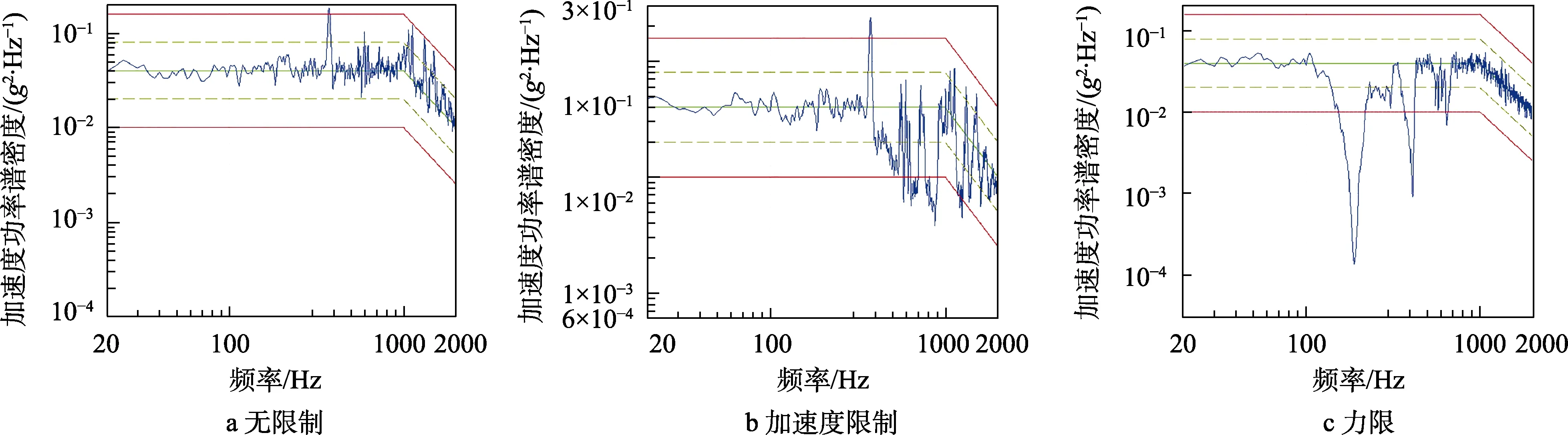
图6 随机振动控制谱 Fig.6 The random vibration control spectrum: a) no limit; b) acceleration limit; c) force limit

无限制、加速度限制及最小包络力限控制时产品加速度监测点的测量图谱见图7。

由图7可知，相对于无限制情况，加速度限制下，测点响应变化不明显，仅受到较小的抑制。在力限情况下，从试品一阶响应处（195 Hz）可以明显看出，该频点处产品共振峰基本被抑制到正常范围，体现出极好的限制效果。

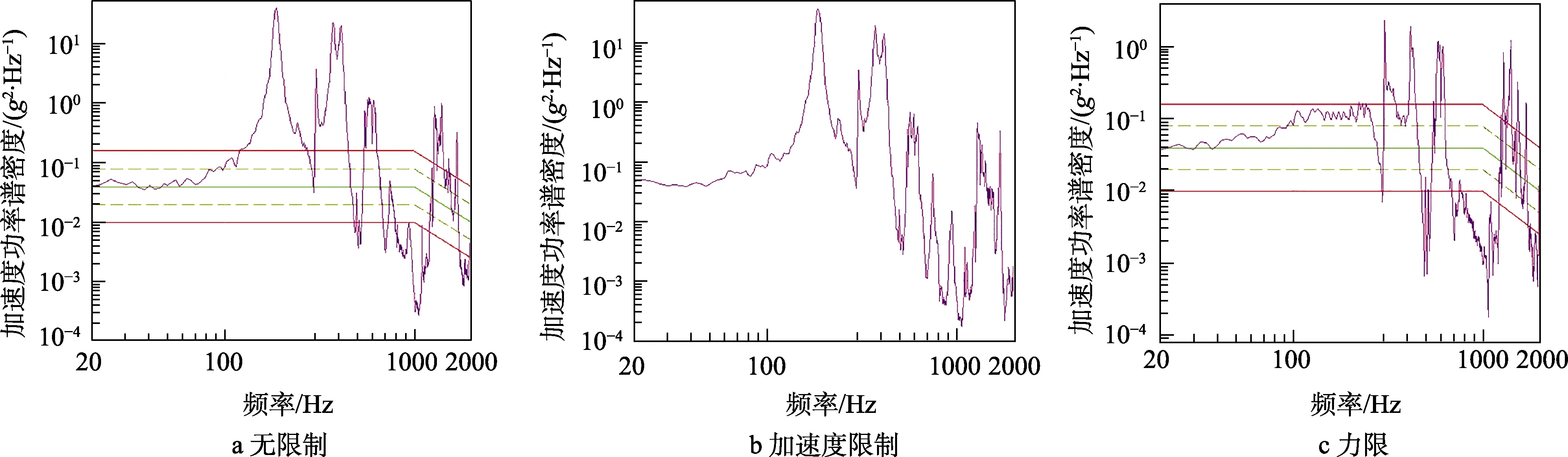
图7 试品测点加速度响应 Fig.7 Acceleration response of measuring point: a) no limit; b) acceleration limit; c) force limit

无限制、加速度限制及最小包络力限控制时产品界面力的测量图谱见图8。

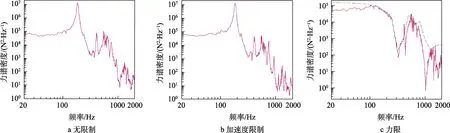
图8 界面力测点响应 Fig.8 Response of interfacial force measurement point when force is limited: a) no limit; b) acceleration limit; c) force limit

由图8可知，相对于无限制情况，加速度限制下，界面力测点在一阶频点处变化不明显，仅在相对高频处（>400 Hz）体现出一定的抑制作用。在力限情况下，界面力基本维持在力限谱之下，界面力响应与限制谱吻合较好，体现出力限谱制定的合理性及准确性。

4 结论

以空间飞行器结构模拟件为试验模型，组建了力限振动控制试验系统，设计了力限控制方程并开展了试验研究，研究结果表明：

1）相对于加速度控制方法，在力限下，控制谱在共振点处出现明显的倒三角下凹曲线，限制效果明显，产品的共振响应明显下降，起到了较好的限制作用。

2）在加速度限制下，控制曲线在共振频点处，特别在高频处，振动控制极不稳定，抑制共振峰效果不明显。在力限作用下，振动曲线整体控制比较稳定，且在预期的共振频带处呈现倒三角下凹现象，下凹峭度比较大，对共振频带处的抑制比较精准。

3）相对于加速度控制方法，从界面力测量响应可以看出，加速度限制对界面力影响不大，但在力限控制下，界面力限制效果较为突出，控制在合理范围。

4）针对不同的力限控制方程，由于半经验法依据工程经验系数制定力限控制方程，虽然有一定的合理性，但只考虑了产品一阶模态频率，没有考虑更多阶的模态，因此制定的力限制谱不够精确，缺乏对频带抑制的针对性。相对于半经验法，简单二自由度法在制定力限条件时，考虑了试品多阶的模态响应，制定的力限条件更具针对性，但简单二自由度法并没有将振源的模态响应考虑在内，因此制定的力限条件不够精细。复杂二自由度法同时考虑了振源和负载的多阶模态及其相互作用，制定的力限控制方程更加精准。

半经验法、简单二自由度法及复杂二自由度法制定条件的基准均依据原始振动加速度试验谱，且限制谱条件采用了极小包络。同时试验结果表明，力限限制相较于加速度限制，其限制效果更为明显。因此，相对于加速度限制，力限控制方法得到的试验结果更趋于保守，在对产品进行具体考核时，应根据产品实际情况对限制谱进行适当修订。