三角矩阵环上的广义Gorenstein投射模

关菡青， 杨 刚

兰州交通大学 数理学院，兰州 730070

Gorenstein同调代数起源于20世纪60年代，是由Auslander和Bridger等人的相关研究成果发展而来．作为有限生成模的推广，文献[1]引入了双边Noether环上G-维数为0的模．20世纪90年代，文献[2]推广了Auslander和Bridger的结果，引入了任意环上Gorenstein投(内)射模和Gorenstein平坦模的概念．2010年，文献[3]引入了环R上X-Gorenstein投射模的概念，其中X是指包含所有投射左R-模的模类，统一了环R上的一些Gorenstein同调模类．

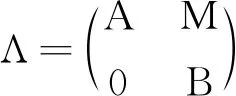
受上述结论的启发，本文引入了三角矩阵环上的Φ(X，Y)-模类，其中X是包含所有投射左A-模的模类，Y是包含所有投射左B-模的模类．由此给出了Φ(X，Y)-Gorenstein投射模的刻画，推广和统一了三角矩阵环上的许多广义Gorenstein同调模类，如投射模类、Gorenstein投射模类、Ding投射模类及其性质刻画等．

1 准备知识

设A是环．本文以A-Mod表示左A-模范畴．无特别声明，所有的模均指左模．

定义1[7]设A是环．如果P是正合序列

其中每个Pi是投射A-模，并且对任意投射A-模P′，HomA(P，P′)是正合序列，则称序列P为完全A-投射分解．如果存在完全投射分解P使得M≅Kerd0，则称A-模M是Gorenstein投射模．

定义2[8-9]设A是环．如果存在A-模的正合序列

定义3[3]设X是A-模构成的类，且包含所有的投射A-模．如果存在A-模的正合序列

定义4设M是A-模，X是包含所有投射A-模的类．定义M的X-分解维数为

注意到，若pdAM<∞，则有X-pdAM<∞．

2 Φ(X，Y)-Gorenstein投射模

定义5设X是包含所有投射A-模的类，Y是包含所有投射B-模的类．令

显然Φ(X，Y)是包含所有投射Λ-模的类．由定义4，如果存在Λ-模的正合列

定义6[6]定义以下函子：

显然p和q是伴随对．

注1以下结论成立：

定义7设M是A-B双模．如果M满足以下两个条件：

(W1) 若Q′是投射B-模的正合列，则M⊗BQ′正合；

(W2) 对任意Y∈Y，X-pdA(M⊗BY)<∞．

则称M是强相容的．

引理1设M是A-B双模．以下结论等价：

证⟹设序列P是A-模的X-完全投射分解

则对任意X∈X，HomA(P，X)是正合序列．由知，存在A-模的正合列

其中Xi∈X，0≤i≤n．用HomA(P，-)作用得到正合列

因为HomA(P，Xi)正合，故HomA(P，M⊗BY)正合．

是A-模的复形，即有以下列正合的交换图

特别地，中间行正合当且仅当上行正合．

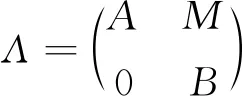
证⟹设则存在Λ-模的正合列

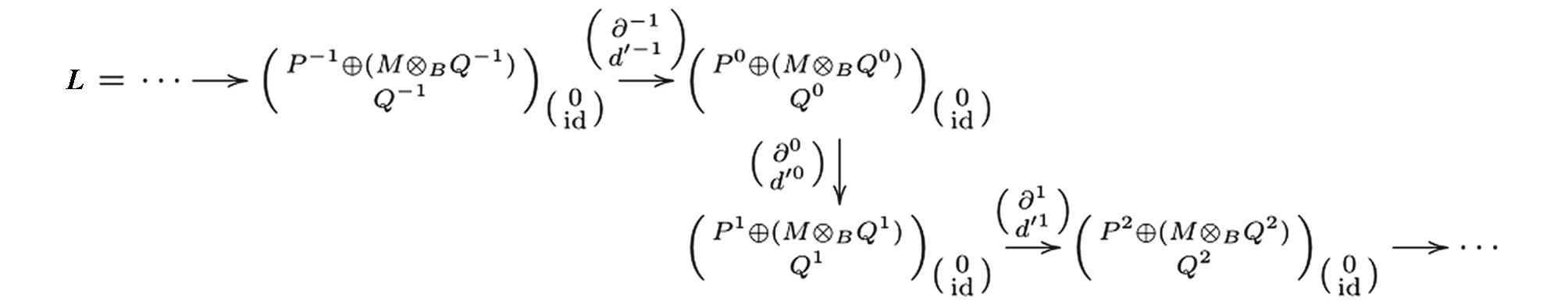
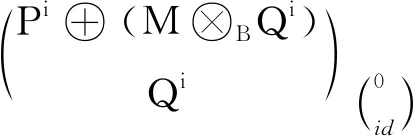
其中Y≅Kerd′0．同时有A-模的正合序列

强相容，易知M⊗BQ正合，因此P正合．于是有列正合的交换图

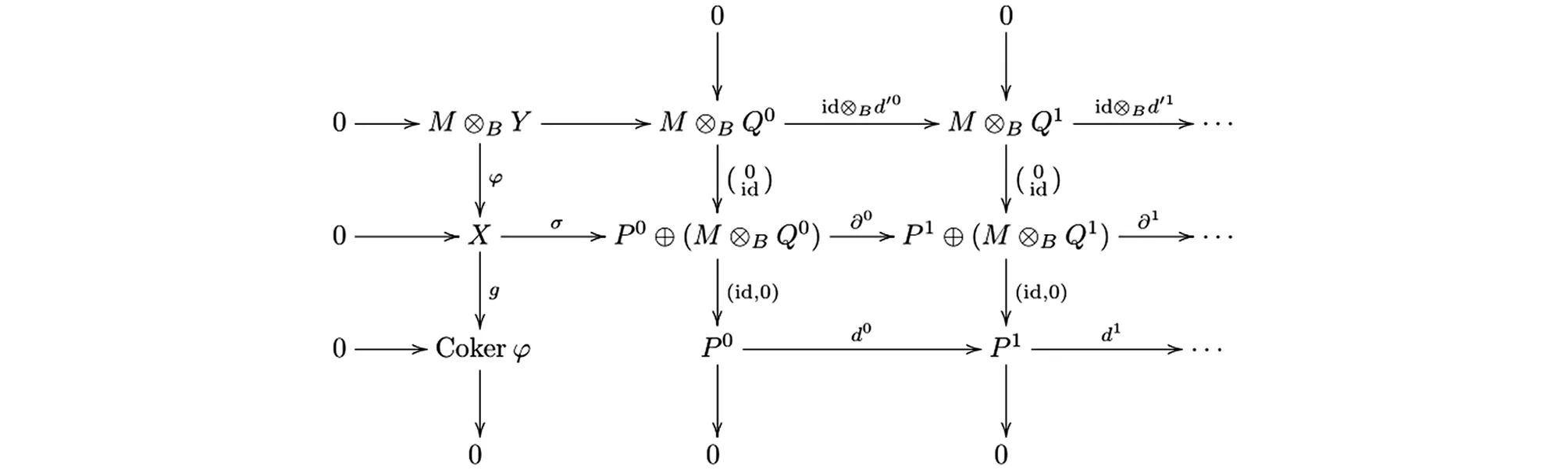
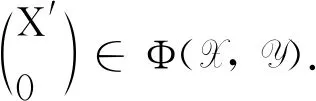
用HomΛ(L，-)作用后得到正合列

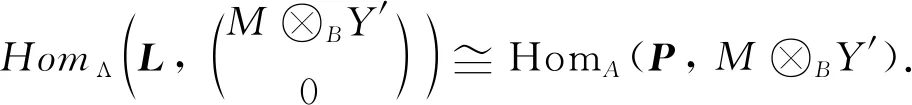
其中每个Qi投射，Y≅Kerd′0，并且对任意Y′∈Y，HomB(Q′，Y′)是正合序列．而M是强相容的，可得M⊗BQ′正合．特别地得到正合列

由于Cokerφ∈G(X)，故有A-模的正合序列

其中每个Pi投射，Cokerφ≅Kerd0，并且对任意X′∈X，HomA(P′，X′)是正合序列．因此有正合列

对偶地可以得到以下行正合的交换图

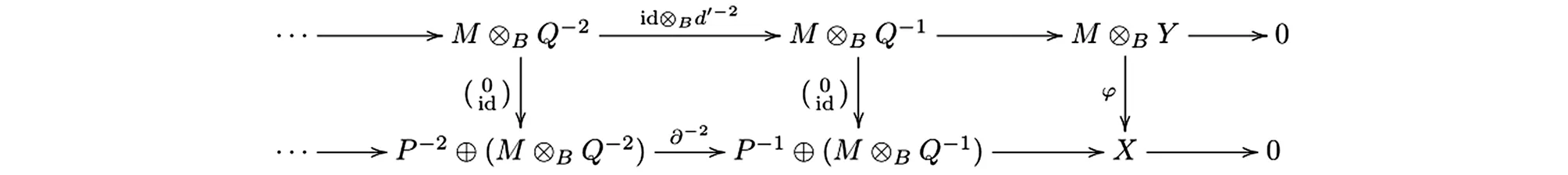
综上所述，可以得到投射Λ-模的正合列

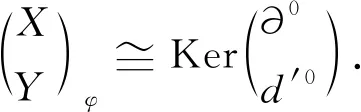
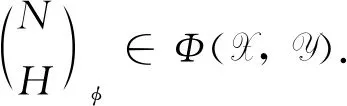
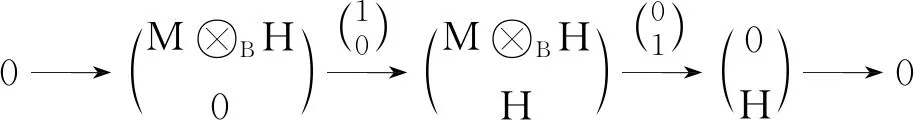
由定理1容易得到以下结论：

推论1[5-6]