基于CUDA架构下的直方图均衡并行算法
2021-12-06肖诗洋孙陆鹏郭宝云
肖 汉, 肖诗洋, 孙陆鹏, 郭宝云
(1.郑州师范学院 信息科学与技术学院, 郑州 450044; 2.东北林业大学 土木工程学院, 哈尔滨 150040;3.山东理工大学 建筑工程学院, 山东 淄博 255000)
0 引 言
在图像的采集、传输和处理等过程中, 经常受到外部噪声和光照不均匀等各种环境影响, 图像质量会严重降低, 有必要对图像进行增强处理[1]。图像直方图是图像处理中一种十分重要的图像增强工具, 在军事、航空、商业等领域有广泛的应用。该算法的理论基础是概率统计, 通过对图像中像素点值的计算对图像直方图进行变换, 从而达到图像增强的目的[2]。图像增强往往要求做到实时、快速,而面对海量图像数据、算法复杂度不断增加, 图像增强的高效快速处理面临着新的挑战[3]。
对于提高图像对比度和直方图均衡算法的性能, 引发了很多学者的关注和研究。为了提高水下图像对比度, Wong等[4]提出了一种采用并行结构的的差分灰度直方图均衡算法。为了在平均亮度保持和对比度增强之间取得折衷, Khan等[5]采用自适应直方图均衡增强血管和背景之间的差异性;陈松等[6]提出了基于数字信号处理器(digital signal processor, DSP)的图像直方图均衡算法的优化方法, 执行效率提升了6.02倍;齐建玲等[7]利用FPGA的并行处理能力, 对直方图均衡算法进行优化设计, 将处理速度提升1倍;占正峰等[8]提出了基于GPU的直方图均衡化并行算法,充分利用GPU的并行处理能力, 获得了24.96倍加速比;Mahmud等[9]利用OpenCL并行计算方式实现了直方图均衡并行算法, 大大减少了系统消耗的时间。
近年来, 随着制程工艺和集成技术的发展, 图形处理器(graphic processing unit, GPU)的计算能力越来越强大。CPU+GPU的计算模式是由CPU负责执行复杂的逻辑处理和事务处理等不适合数据并行的任务, 由GPU负责进行密集型大规模数据并行计算[10-11]。统一计算设备架构(compute unified device architecture, CUDA)是NVIDIA公司于2007年提出,用于GPU计算的新的软硬件架构, GPU在架构中被视为一个数据并行计算设备, 对要处理的计算任务进行分配和管理[12]。
本文利用CUDA来解决在异构计算设备上进行大规模图像的直方图均衡处理问题, 提出了一种基于CUDA架构的高效直方图均衡并行算法, 在保持其串行算法精度的同时, 取得了61.58倍的加速效果。
1 算法的软件模型
1.1 CUDA异构编程模型
CUDA是一种新的基础异构架构, 该架构可以使用GPU来解决工业、商业以及科技方面的复杂计算问题。它是一种完整的图形处理器通用计算(general-purpose computing on GPU, GPGPU)的解决方案, 提供了硬件的直接访问API, 而不必像传统方式一样须依赖图形用户接口来实现GPU的访问。在架构上采用了一种新的计算体系结构来利用GPU提供的硬件资源, 从而给大规模的科学计算应用提供了一种比CPU更为强大的计算能力。CUDA采用C语言作为编程语言以提供大量的高性能计算指令, 使开发者能够以GPU的强大计算能力为基础, 建立起一种更高效率的密集数据计算解决方案。由于科学计算应用具有较高的计算密度, 因而, GPU可通过计算隐藏存储器访问延迟, 而不必使用较大的缓存器。用大规模并行处理器和CUDA C扩展语言进行通用计算的工作, 这种新的GPU编程模式就是“GPU计算”。
1.2 算法原型
直方图均衡化是以概率累积函数变换法作为基础, 将已知图像的概率分布转变为均匀概率分布, 从而获得一幅视觉增强后质量较好的图像。经过直方图均衡化处理, 可使原图像的灰度分布转换为一种均匀分布方式, 使图像的细节更容易辨识。设pr(r)表示待处理图像的概率密度函数,ps(s)表示经过直方图均衡化后的图像概率密度函数, 图像总灰度级数为L, 由概率理论可得
ps(s)=pr(r)|dr/ds|,
(1)
由式(1)得到ps(s)中变量s的表达式为

(2)
由莱布尼茨准则可知,

=(L-1)pr(r),
(3)
把式(3)代入式(1), 得到
(4)
在图像处理中, 当图像像幅大小为M×N时, 其直方图可表示为
(5)
且pr(rk)满足
(6)
其中:pr(rk)表示图像中灰度级为rk的分布概率;nk表示灰度级为rk的像素个数,即对灰度级为rk的投票;MN表示像素总数。
直方图均衡化处理就是通过某种函数映射, 将原图像的灰度级分布从集中转变为均匀。设T为映射算子, 则有
s=T(r),
(7)
式(7)满足s在0≤r≤1内单调递增, 且0≤s≤1。直方图均衡化后的概率密度函数ps(sk)是一种均匀概率密度函数。所以, 图像经过映射算子的作用, 进行直方图均衡化操作后, 直方图信息将显示出均匀性。累计分布函数的表达为

k∈[0,L-1],
(8)
取整扩展
sk=int(sk+0.5)。
(9)
1.3 程序性能瓶颈剖析
根据测试方法, 为保证测试时间更加准确, 实验的测试结果取100次运行结果的平均值并记录。为了确保测试数据真实可靠, 实验时保证本轮测试具有独占性。在取得算法各步骤的运行时间及整个算法的执行时间之后, 计算得到直方图均衡算法中各主要步骤耗时在整个算法中所占比例, 具体数据如表1所示。
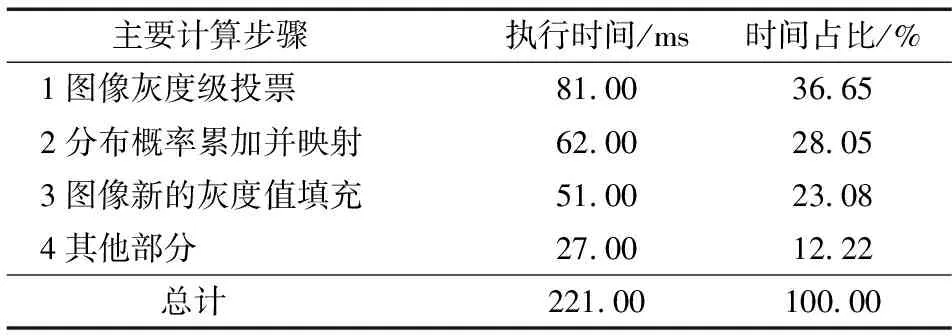
表1 算法各步骤运行时间占比
可见, 直方图均衡算法耗时主要集中在步骤1, 其次是步骤2和3。以3 268×3 689图像像幅大小为例, 这3个步骤的运行时间在串行算法总执行时间中所占比例为87.78%, 其他步骤处理时间只占算法总运行时间的12.22%, 说明步骤1~3是串行算法的性能瓶颈所在。如果采取一定并行措施能够大幅降低直方图均衡算法的处理时间, 就可以获得良好的加速效果。
1.4 并行化可行性分析
直方图均衡算法的热点主要包含3部分: 统计图像中每个灰度级上的像素数量、计算图像中每个灰度级的分布概率并进行累加映射, 以及像素点灰度值映射结果的填充。通过分析发现: ① 每个灰度级上的像素数量的统计计算可相互独立进行, 存在一定的并行性, 但由于图像灰度级L≪M×N, 可采用原子操作方法和同步机制解决当多线程同时将统计结果写至直方图数组时导致的访存冲突问题。这是直方图均衡算法中计算量最大的部分, 如果对其进行并行化, 会极大地提高算法的运算速度。② 在L个灰度级上进行的操作具有较强的并行性: 分配一个线程进行某个灰度级分布概率的计算, 根据灰度级所在的等级进行前缀和式的概率值求和, 并依据映射规则完成灰度值的映射。③ 遍历图像像素点用新的灰度映射值填充相应像素点: 可以设计合适的数据结构, 通过CUDA并行设计方法对其进行并行化。经分析可知, 图像灰度值数量统计、分布概率累加并映射和图像新的灰度值填充3部分都可以并行化。
2 直方图均衡算法的CUDA实现
2.1 并行算法描述
根据CUDA计算架构的特点, 设在单指令多线程(single instruction multiple thread, SIMT)模型中启动M×N个线程, 每一个线程只负责处理一个像素的转换, 然后把结果存储到对应的位置。整体的并行化思路如下。

算法 SIMT模型上的直方图均衡并行算法输入: 图像像素矩阵srcImageData输出: 均衡化后图像像素矩阵desImageDataBegin In CPU: Input image array srcImageData In GPU:forj=0 to (M×N-1) par-do t ← srcImageData(tid) Add grayscale value t to the corresponding grayscale level counter end for for i=0 to(L-1) par-do Calculate probability density function of gray level Calculate the prefix sum of the probability density function of gray level Calculate grayscale mapping end for for j=0 to (M×N-1) par-do t ← srcImageData(tid) Update the mapped grayscale value corresponding to the grayscale value t to the corresponding pixel end for In CPU: Output equalized image array desImageDataEnd
假设图像像幅为M×N, 如果用CPU实现直方图均衡串行算法, 则是通过遍历整个图像像素数据进行计算, 因此, 算法时间复杂度是Ο(M×N)。采用GPU的多线程对直方图均衡算法进行并行计算, 一个线程负责处理一个像素点。因此, 运算时间将减少到Ο(1), 这是一个恒定的等级。核函数中处理所有的像素点如果没有并行执行, 则每个线程执行直方图均衡内核函数最少(M×N)/ST次, 其中ST是线程的数量。此时, 时间复杂度将为Ο((M×N)/ST)。然而, GPU中可以保持的活动线程量很大, 即ST总是一个很大的量值。所以, 存在直方图均衡并行算法时间复杂度Ο((M×N)/ST)≪Ο(M×N)。
2.2 方法设计
图1具体说明了基于CUDA架构的直方图均衡化算法的过程。主机端首先获取输入图像的参数, 同时对GPU设备进行初始化, 包括设备的选择和设置。随后, 主机申请图像数据、图像均衡数据、图像各灰度级概率统计和图像各灰度级映射需要的信息存储空间, 将图像数据由主机端内存拷贝到设备端的全局存储器。在GPU中完成数据的网格处理任务。在设备端通过获取CUDA二维线程索引, 并根据灰度级投票、灰度级概率密度函数和灰度级映射的运算任务, 计算出当前线程对应的数据地址。让每个线程块执行一个子图像块, 进行一个子直方图均衡化转换, 接着合并每个线程块的子直方图均衡转换结果, 得出总的直方图均衡化结果。将设备端完成运算任务后的图像均衡化结果传输到主机端内存, 主机完成最终的图像均衡结果的显示。
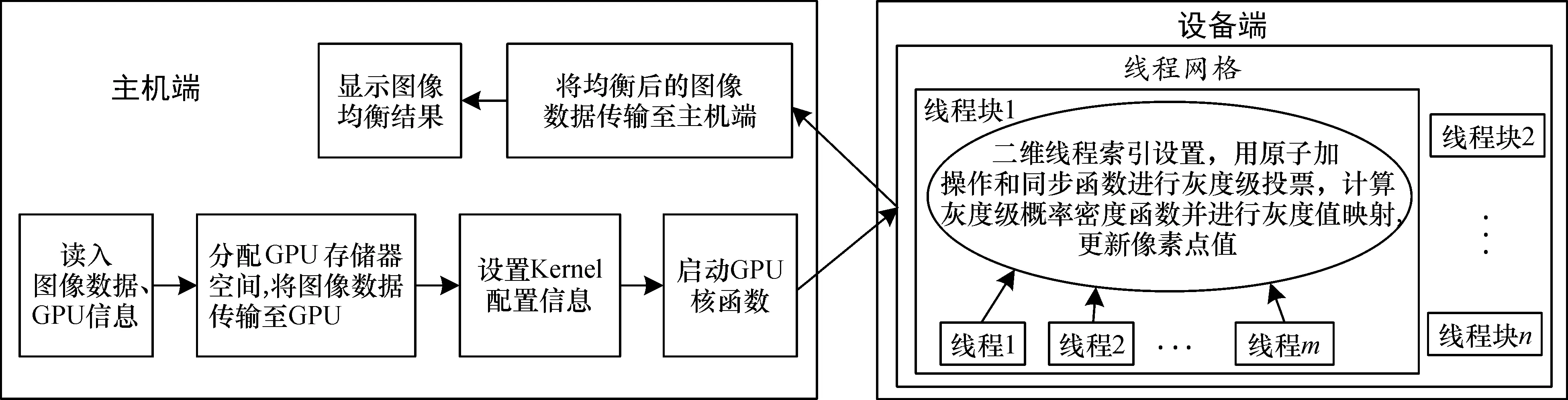
图1 直方图均衡并行算法流程图
2.3 并行计算方法
2.3.1 核函数并行维度的设计 根据按行连续排列存储图像数据的特点和CUDA网格模型的特点, 对内核计算的图像处理任务进行粗粒度和细粒度的划分。以子图像块作为划分依据, 将图像划分为互不重叠的格网区域, 实行粗粒度的并行,再在各子图像块中按照像素为单位再行划分, 实行细粒度的并行。
内核计算任务并行划分见图2。一个Kernel对应一个线程块网格, CUDA中的Kernel是以线程块网格(Grid)的形式组织。Grid包含若干个线程块(Block), Block又包含若干个线程(Thread)。直方图均衡内核任务划分映射到上述线程模型: 整幅图像映射到Grid上, 一个子图像块映射到一个Block, 子图像块中的像素点映射到Block中的Thread。
一是土壤结构改变问题。果农在栽培管理过程中化肥施用过量,有机肥施用量少,没有重视微量元素微肥,造成土壤肥力下降,土壤中各种元素失衡;二是大面积无限制的使用化学农药防治病虫害和过量使用生长调节剂,残留物对环境造成了污染;三是废弃物处理问题。不易降解的农用地膜、套袋薄膜、农药化肥包装袋及其它田间废弃物不经任何处理就随意丢弃在道路旁、江河里,臭气熏天、蚊蝇滋生,造成大面积环境污染[2]。
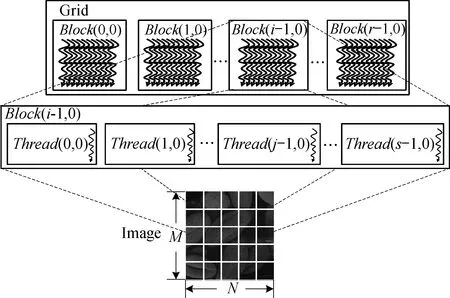
图2 直方图均衡内核任务并行划分示意图
线程和线程块的划分对并行算法的效率影响很大。CUDA中主要通过分配线程块和线程来实现直方图均衡并行计算, 具体用粗粒度并行和细粒度并行划分线程和线程块。
① 粗粒度并行。在图像直方图均衡并行处理时, 将一幅图像分成一系列子图像块, GPU线程网格由二维线程块网格组成。每一个线程块可以独立处理相应的子图像块。具体分配线程时采用二维线程块网格进行线程划分。假设M、N分别是图像的高和宽, 每个线程块能够分配nTX×nTY个线程, 则需要分配BX×BY个线程块, 其中BX=(M+nTX-1)/nTX,BY=(N+nTY-1)/nTY, 在GPU内核函数配置时, 进行线程块和线程分配, 即
Dim3Threads(nTX,nTY)
Dim3Blocks(BX,BY)
② 细粒度并行。图像中每个像素点数据的计算都是独立的, 只要在并行运算平台CUDA中为每个像素点分配一个线程, 每个线程并行地根据式(1)和式(4)即可计算完数据项。实现并行计算数据项需要进行线程与像素点映射, 即
tidx=threadIdx.x+blockIdx.x×blockDim.x
tidy=threadIdx.y+blockIdx.y×blockDim.y
其中,threadIdx.x和threadIdx.y为某个线程块中的线程分别在X和Y方向的索引,blockIdx.x和blockIdx.y为某个线程块在网格中的X和Y方向的索引,blockDim.x=BX,blockDim.y=BY。这样, 每一个线程均对应一个像素点, 同时计算每个像素点的数据项。
2.3.2 灰度级投票的并行设计 通过对各像素投票值累加可获得每个灰度级的最终投票值。而配属线程内部的寄存器在网格内的线程间不可见, 无法通过计数器完成投票的累加操作。此时就需要一种操作, 既可以保证各线程之间的计算互相独立, 又可确保将最后的统计结果进行累加。鉴于GPU中每个线程访问同一个全局存储器地址时, 在计算能力为1.2以上的设备中, half-warp块所请求的具有4 B数据字的同一地址的模式都会实现合并访问。因此, 可以采用全局存储器来进行投票累加数据的存取, 用来完成每个灰度级的累加, 且可以保证线程之间计算的独立性,如图3所示。
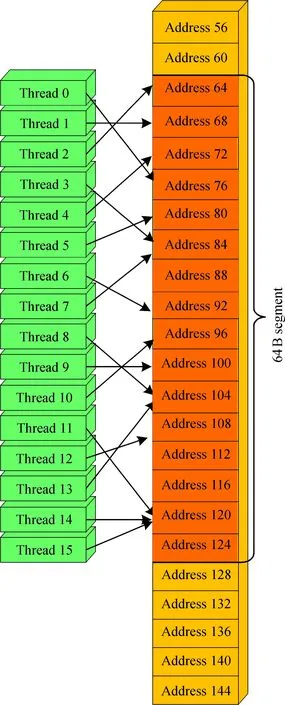
图3 在一个64 B的分区内的随机float存储器访问, 得到一个存储器事务
但是全局存储器的使用会带来未合并访问的问题。如果在half-warp中有部分线程对存储器地址的访问出现了交错或起始地址未对齐, 就会造成未合并访问。投票过程中一旦出现未合并访问情况, 会致使全局存储器访问效率降低, 算法运行的速度将遭受严重影响。为了克服这个问题, 采用原子加机制来执行投票累加的过程。在CUDA中开辟L个全局存储器存储空间, 每个存储空间负责一个灰度级的统计。线程网格内开启BX×BY×nTX×nTY个线程, 每个线程根据自己对应像素点位置上灰度值进行投票。采用CUDA内部的原子加操作统计, 在类别数组上取数据并执行加法操作。同步线程块内线程, 得到最终投票数组。原子加操作可保证在某个线程对某个灰度级进行累加的操作过程中, 不会被线程调度机制打断。也就是说,当多个线程同时访问灰度级数据的同一位置时, 保证每个线程能够实现对共享可写全局存储器数据的互斥操作。在整个投票累加器工作期间都不会切换到另外的线程, 意味着投票过程是串行执行。在一个线程执行对某个存储器地址的累加运算后, 其他的线程才能再执行对该存储器地址的累加操作,于是便解决了未合并访问的问题。
2.4 性能优化
不同线程块的布局对于存储器访问的性能不相同, 每个线程块的线程数量应为warp大小的整数倍。为了避免因warp块填充不足而造成的计算资源浪费, 系统中应保持足够多的线程块数量。根据全局存储器合并访问和分区冲突的要求, 建议每个线程块使用128~256个线程, 这样可以提高访问全局存储器的效率。尽可能同时执行更多的线程, 就越容易隐藏存储器延时。线程块应尽量使得X和Y方向的维度是warp大小的倍数。表2中显示了图像像幅大小为5 234×5 648时, 在线程块中设置不同数量线程时的系统运算时间。可以看出, 线程块中的线程数量不同, 其对应的运算时间有差异。对于本例,当线程数为16×16时, 系统性能最优。运算中,为每个线程块分配更多线程可实现有效的时间分割, 从而提高运算速度; 但线程数量过多, 每个线程可用的寄存器就越少, 实际能够被调度到流多处理器上运行的线程块也越少, 甚至造成Kernel由于寄存器不足而无法启动。

表2 线程块大小对运算速度的影响
3 实验测试和结果分析
3.1 实验运算平台
本研究的硬件实验平台CPU为Intel Core i7-7700(四核心), 主频3.6 GHz, 系统内存为16 GB。GPU主要配置参数如表3所示。操作系统为微软Windows 8.1 64 bits; MATLAB R2018b; Microsoft Visual Studio 2017集成开发环境; OpenMP 3.0的多核处理器支持环境; CUDA Toolkit 8的编译支持环境。

表3 NVIDIA GTX 1060配置参数
3.2 实验数据
为了进行多组数据的对比实验, 需要对原始图像数据进行预处理, 通过裁剪获得图像大小分别为356×687、1 256×1 587、2 868×2 745、3 268×3 689、4 253×4 725、5 234×5 648和7 646×7 862共7组实验数据。图4、5、6分别是对像幅大小为500×500的暗图像、亮图像、低对比度图像进行直方图均衡处理的结果和相应的直方图。

图4 暗图像处理效果
本文共设计3种实验以验证图像直方图均衡算法: 第一种实验运行基于CPU平台的串行图像直方图均衡算法;第二种实验运行基于多核CPU平台的OpenMP并行图像直方图均衡算法;第三种实验运行在GPU平台的并行图像直方图均衡算法。针对3组测试图像, 多次运行3种直方图均衡系统, 计算出各组实验的直方图均衡平均耗时, 数值结果保留小数点后两位, 串行算法执行时间与并行算法执行时间对比如表4所示。

表4 不同计算平台下直方图均衡算法执行时间
定义加速比
s=Ts/Tp,
(10)
其中, 串行算法的执行时间为Ts, 并行算法的执行时间为Tp。将串行算法执行时间和并行算法执行时间相比即为加速比。加速比反映了在相应并行计算架构下的并行算法相比CPU串行算法系统执行效率的改善情况, 能够对实际系统的速度进行客观评价, 如表5所示。

表5 不同计算平台下直方图均衡并行算法性能对比

图5 亮图像处理效果
3.3 有效性验证
本文以在CPU串行计算中实现的图像直方图均衡算法作为进行GPU移植和优化的基准CPU程序, CUDA算法系统的各方面参数与该基准程序保持一致。因此, 有效性验证只和该CPU串行算法的运行结果进行比较。
3.3.1 宏观层面结果一致性 由图6的实验结果可知, 在3组实验中原始图像对比度都较低且图像暗淡, 而经过直方图均衡算法串行和并行处理后图像都比原始图像要清晰明亮, 具有较高的对比度。图像直方图均衡串行系统和并行系统的运行结果相同, 无肉眼可辨的差异。

图6 低对比度图像处理效果
3.3.2 微观层面结果一致性 由图4~图6的实验结果可见, 在每一组实验中的直方图均衡串行处理和并行处理的直方图对应的数据相同, 即相同灰度级的像素数一样。在3组实验中, 原始图像的直方图分布并不均匀, 经过直方图均衡算法串/并行处理后的图像直方图分布均匀, 保持了处理结果的一致性。
3.4 实验数据分析
3.4.1 系统性能瓶颈分析 在直方图均衡算法处理过程中,需要对原始图像数据进行M×N次存储器读取, 对直方图均衡图像增强数据进行M×N次存储器写入操作。由于M×N=3 268×3 689, 每个像素值分配存储空间大小是2 B, 所以, 存储器存取数据总量约为0.048 GB。除以Kernel实际执行的时间0.000 312 s, 得到的带宽数值是约154 GB/s, 这已经接近GeForce GTX 1060显示存储器的192 GB/s带宽了。可见, 基于CUDA架构的直方图均衡并行算法的效率受限于全局存储器带宽。
3.4.2 不同架构下直方图均衡算法运算时间分析 在3种计算平台上对不同像幅大小的实验图像进行直方图均衡处理, 将CPU串行运行时间和在两种不同并行计算架构下的运行时间进行对比, 如图7所示。当图像像幅大小相同时, 在不同并行计算平台上执行时间相对CPU串行执行时间都有不同程度的缩减, 即均获得了加速效果。对于像幅大小为7 646×7 862的直方图均衡串行运算时间为4 106.00 ms, 在OpenMP计算平台下运算时间缩短为1 186.70 ms, 而在CUDA架构下的并行计算平台上运算时间则大幅缩减为66.67 ms。
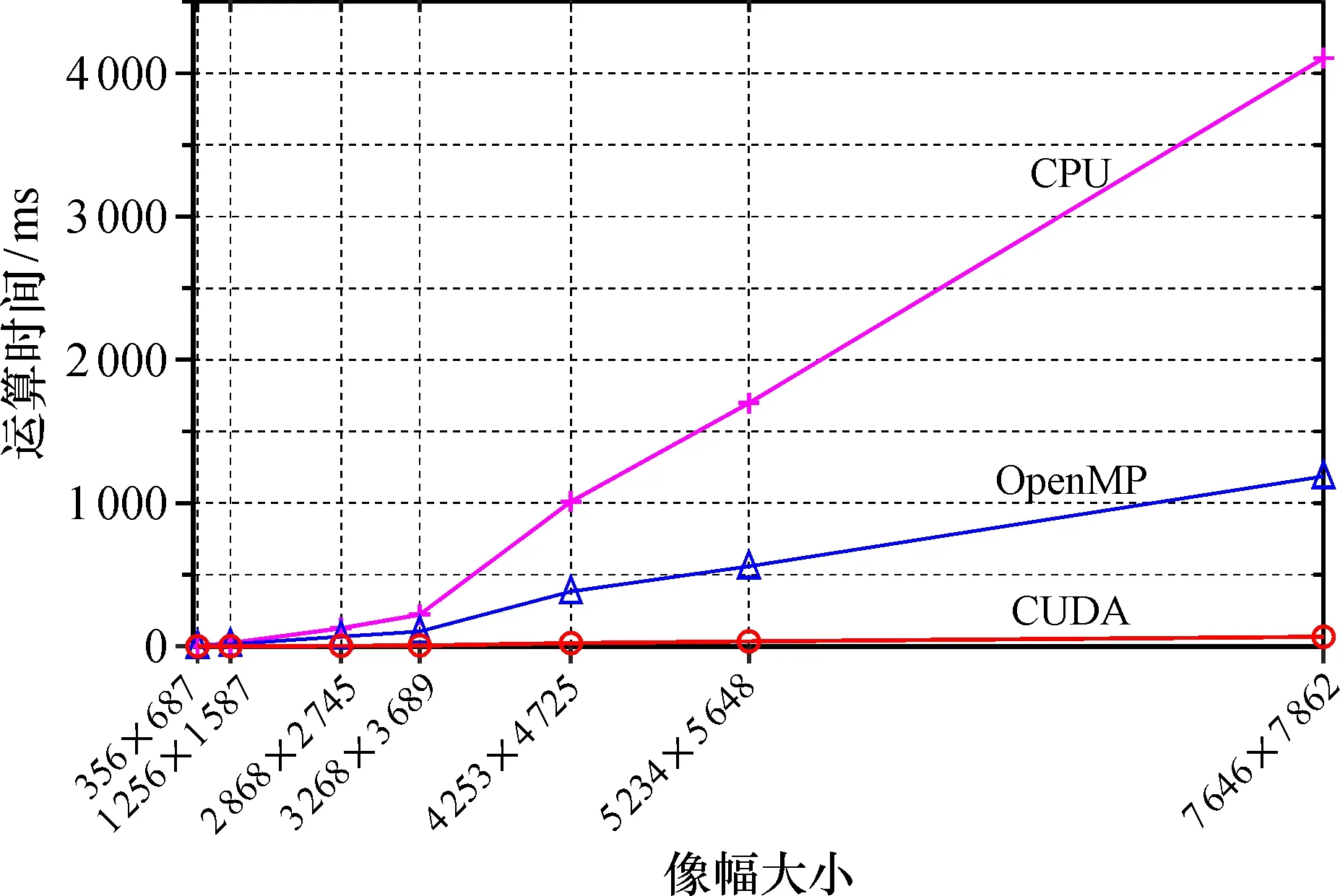
图7 不同计算平台下直方图均衡算法运算时间对比
在相同像幅大小下, 利用OpenMP并行处理后的直方图均衡算法的运算时间相比单线程的串行算法运算时间有明显的减少,并且在相同的线程数下随着图像规模的增大, 运行时间也越来越长, 基本符合线性增长的趋势。
当图像像幅较小时, 在基于CUDA的直方图均衡并行算法中, 由于启动的线程计算量不满载, 大部分时间消耗在系统调度方面。GPU高性能计算的优势没有展现, 运算时间与CPU运算时间差别不明显; 随着图像像幅的增大, 每个线程的计算量渐渐满载, 在系统调度方面消耗的时间比例降低, GPU并行度提高, 加速比上升。
3.4.3 并行计算架构下直方图均衡算法加速效果对比分析 由图8可知, 基于多核CPU的直方图均衡算法取得了一定的加速效果。相较于串行算法, 随着像幅大小的增大, 总体保持着近2~4倍左右的加速。由于受到CPU核数的制约, OpenMP并行算法很难达到比较高的加速比。而GPU并行算法的加速效果则十分明显, 并行算法在处理7 646×7 862大小的图像时, 实现了比串行算法快61.58倍的加速比, 极大程度节约了运算时间。同时, 随着图像规模的增大, 并行算法所得到的加速比也在不断增大, 可以很好地满足实时性要求。但是, 并行处理性能的提升是一种非线性增长, 且随着像幅规模的进一步增加, 缓慢上升的趋势十分明显。出现此现象是由于主机与设备间的数据传输带宽远低于设备之间的数据传输显存带宽,主机内存和GPU存储器间的交互数据过程造成了一定的时间开销。当图像像幅规模不大时,这部分开销对系统的计算时间有较大影响;只有当图像规模较大时, 数据交互时间所占比例较小, GPU并行计算时间足以抵过系统传输延迟开销, GPU加速的效果才凸显出来。

图8 直方图均衡并行算法加速比趋势图
将本文算法的整体加速效果与文献[6-9]进行对比。文献[6]中基于DSP的直方图均衡并行算法的性能提升6.02倍, 文献[7]中基于FPGA的直方图均衡并行算法的性能提升1倍, 文献[8]中基于GPU的直方图均衡并行算法最大获得了24.96倍的加速比, 文献[9]在处理图像大小为100×100时获得了最大加速比是12.32。而根据表5的测试结果可以看到, 本文基于CUDA加速的直方图均衡并行算法获得了61.58倍加速比。因此, 相比文献[6-9]中的算法, 本文并行算法取得了更好的加速性能。
4 结束语
本文对基于CUDA的图像直方图均衡算法进行了深入研究。首先对直方图均衡处理技术的时域算法进行了分析, 以寻找算法的热点; 然后充分分析直方图均衡算法性能瓶颈步骤的可并行性; 最后, 针对CUDA编程模型与直方图均衡算法特点, 提出了基于CUDA的直方图均衡并行算法的优化方案。该方案利用直方图均衡算法各个计算步骤的不同特征, 与CUDA存储器访问机制相结合, 提高数据计算速度。针对方案中数据和任务的并行度, 阐述了按照图像格网区域进行粗粒度并行和子图像块中像素点进行细粒度并行的两级并行处理技术, 最大限度地利用了GPU并行计算资源。根据GPU硬件特点, 采用原子加操作完成了并行投票累加的过程, 并充分利用了全局存储器合并访问的特性, 提高了运算速度。实验表明, 使用本文并行设计方案, 与传统CPU实现方式相比最大获得了61.58倍加速比, 拥有了更高的图像处理效率。
为了更好地增强图像的局部细节, 今后将采用基于子块重叠的局部直方图均衡算法来得到最优的增强效果。同时, 利用微分方程模型和最优化模型描述直方图均衡算法也是一个重要的研究方向[13-16]。下一步需要通过对算法的深入剖析, 尽可能优化数据的存储, 研究多GPU协同计算机制, 利用更强计算能力的GPU计算设备或GPU集群提升算法的性能。
