基于降雨资料的雨量预警指标阈值求解模型
2021-12-06龚云柱周兰庭柳志坤
龚云柱,周兰庭,柳志坤
(1.河海大学水利水电学院,江苏 南京 210098; 2.青岛市发展和改革委员会,山东 青岛 266000;3.青岛市经济发展研究院,山东 青岛 266000)
在农村基层防汛预报预警体系建设中,临界雨量预警是一个重要环节,其指标的计算具有重要的意义。国内外学者对洪涝灾害不确定因素产生的综合影响开展了大量的研究,明确指出临界雨量是洪涝灾害预报预警的筑基石[1]。临界雨量法是采用临界雨量作为预警指标进行洪灾预警的方法,一般适用于集雨面积小,洪水组成单一,区域降雨一致性较好,降雨与洪水有关联性的小流域地区[2]。临界雨量法包括以数据统计分析为核心的统计学法和以水文学及水力学物理机制为主的水文水力学法[3]。统计学法主要包括单站/区域临界雨量法、内插法、比拟法和降雨灾害同频率分析法等,而水文水力学法主要包括水位流量反推法、降雨驱动指标法、动态临界雨量法、降雨径流关系曲线插值法及分布式模型法等[4]。对于临界雨量指标的确定,王燕云等[5]利用支持向量机回归拟合算法模型推求出河南新县的临界雨量,提高了预测精度;陈真莲等[6]采用区域临界雨量法和水位反推法综合分析,确定了广东省连州瑶安小流域临界雨量指标值;翟晓燕等[7]结合分布式水文模型和情景分析法得出了安徽省岳西流域的山洪灾害临界雨量集合。在降雨、地形地质、经济社会等因素影响下,山丘区山洪灾害预警研究备受学者关注,但是对于平原区洪涝灾害研究较少,使平原区洪涝灾害预警成为防汛预报预警建设的薄弱环节[8-9]。为此,本文结合雨量预警指标阈值研究进展,基于临界雨量法和降雨时间序列的分形特性,研究雨量预警指标阈值在防洪防灾中的时效性,提出了基于区域临界雨量法-降雨灾害同频率法-重标极差(R/S)分析法的求解模型,并应用于江苏省泰兴市汛期降雨时间序列进行分析,验证了该模型在平原区洪涝灾害预警中的实用性。
1 模型建立
1.1 区域临界雨量法
对于水文站点分布松散、数量较少地区,比较适用区域临界雨量法分析预警指标,该方法较单站临界雨量法更精确。区域临界雨量法是通过研究区各站点发生洪涝灾害场次、雨量数据计算面平均雨量,来确定预警雨量的方法。首先,根据洪涝灾害调查资料,统计研究区各雨量站的雨量资料来确定引起洪涝灾害降雨过程的起止时间(从连续3 d日降水量均不大于1 mm,第4天出现日降水量大于1 mm的时间开始到洪灾结束的时间);其次,在各次降雨过程中逐次搜寻、统计1/6 h、1/2 h、1 h、6 h、12 h、24 h最大雨量和过程总雨量,并记录起止时间,如果统计时间段跨度大于过程时间长度,则不统计其最大雨量和起止时间,但须记录其过程总雨量;最后根据以下过程确定临界雨量阈值[4]。
a.区域临界雨量初值的确定。假设研究区域内共有S个雨量站,统计出各雨量站N次洪涝灾害不同时长的雨量。设Rtij为第i个雨量站发生第j次洪涝灾害时长t(t=1/6 h,1/2 h,1 h,6 h,12 h,24 h)内的最大雨量,统计区域内N次洪涝灾害时长t内最大面平均雨量的最小值,即为不同灾害场次时长t内区域临界雨量初值:
(1)
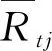

(2)
降雨过程中,区域面平均雨量在[Rt临界,Rt]范围内,就可能会发生洪涝灾害[11]。[Rt临界,Rt]为区域临界雨量阈值,可作为判别区域内有无洪涝灾害发生的定量指标。
1.2 降雨灾害同频率法
降雨灾害同频率法以假设区内洪灾与降雨频率相同为前提,确定相同频率下的雨量设计值作为洪灾预警值的方法。此假设在选样时需考虑超定量的问题,依据文献[5],结合实测资料确定的临界雨量值与区内设计雨量值对比分析可避免选样(超定量)时存在的问题,此方法对本研究适用。首先调查历史洪涝灾害事件,确定降雨资料统计年份[a,b]期间发生洪涝灾害场次N,分析洪灾的致灾频率(P=N/(b-a+1));其次结合降雨统计资料选定样本序列(假设样本数为n)进行参数估计分析,确定该样本在频率P下的雨量设计值,临界雨量初值取与洪灾频率相同的雨量设计值[12],对比分析周边邻近地区的临界雨量和文献[13]中的设计雨量,选取最小值确定为临界雨量值。
在参数估计计算中,运用适线法[14]确定相关参数。首先对由大到小排列的样本序列分别计算经验频率,并将经验频率数据点绘在频率格子上;然后选择皮尔逊Ⅲ(P-Ⅲ)型分布曲线,用适线法进行无偏估计,确定样本均值、变差系数Cv初值,进一步对经验数据点拟合,得到拟合效果好的变差系数Cv及Cs/Cv(Cs为偏态系数),再由下式计算出频率为P时时长t的设计雨量xt,P:
xt,P=x*(1+φPCv)
(3)
式中:x*为样本均值;φP为由P-Ⅲ型频率曲线得到频率P下的离均系数值。
因水文统计过程雨量时长为1 d,求解不同时长雨量需对其进行时长雨量转换。本文采用暴雨公式[4]计算xt,p:
(4)
式中:SP为单位历时的暴雨平均强度;x24,P为频率为P时24 h的设计雨量;n1、n2为暴雨递减指数,本文取n1=0.49,n2=0.74[15]。
对于不同研究区,计算方法有所不同。要确定研究区内发生洪涝灾害的临界雨量指标,需统计全区各雨量站获取的统计资料中逐年24 h最大雨量值,计算全区逐年24 h最大面平均雨量值,对其进行排序并计算经验频率,再进行参数估计确定不同频率下的雨量设计值,最后根据计算的致灾频率选定雨量设计值作为全区的临界雨量值。要确定研究区内各水文站分辖区发生洪涝灾害的临界雨量指标,需统计各分辖区雨量站获取的统计资料中逐年24 h最大雨量值,确定各站点临界雨量值,最后用点面折算系数确定各分辖区临界雨量值。
1.3 R/S分析法
R/S分析法[16]最早被英国水文学家Hurst用于水库与河流之间进出流量的分析,其中Hurst指数为时间序列的极差与标准差的比值。R/S分析法是一种合理预测事物变化趋势的新方法,该方法研究的系统所需要的假设条件很少,被广泛应用于时间序列的分析[17]。对于长度为N的样本时间序列{Xj|j=1,2,…,N},将其等间距分割成长度为τ(τ≥2)的M个连续不重叠的子区间Ym(m=1,2,…,M),则有τM=N。设任意子区间元素为xi(i=1,2,…,τ),其极差、标准差、Hurst指数计算公式[18]分别为
(5)
(6)
lg (R/S)=Hlgτ+Hlgα
(7)
其中
式中:R为极差;S为标准差;H为Hurst指数;α为不依赖于H的变量,是反映自然现象固有特性的回归系数。
Hurst指数反映事物发展过程的长记忆性程度与事物发展过去、现在和未来之间的内在联系,可确定时间序列的自相似性和长程相关性[19]。
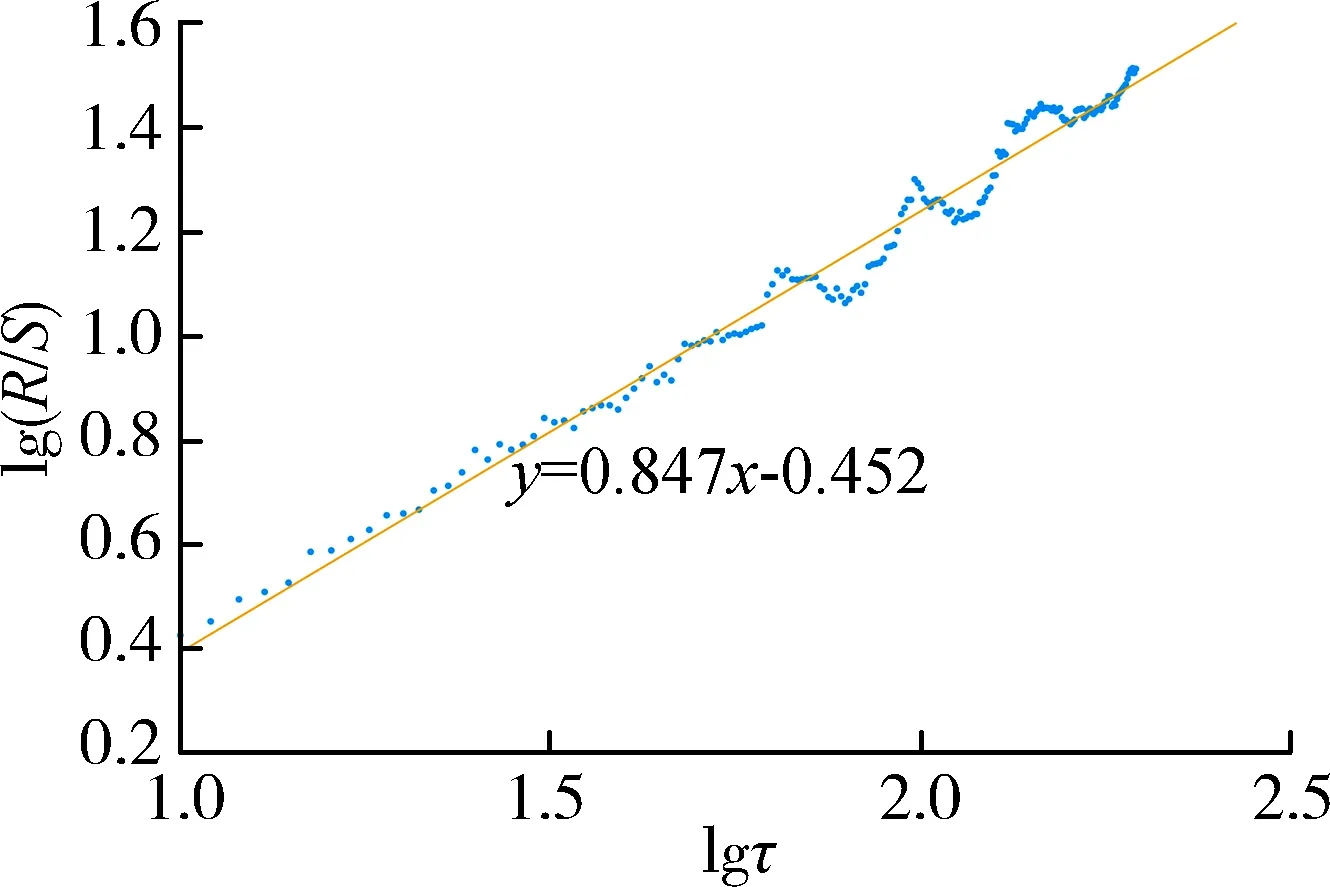
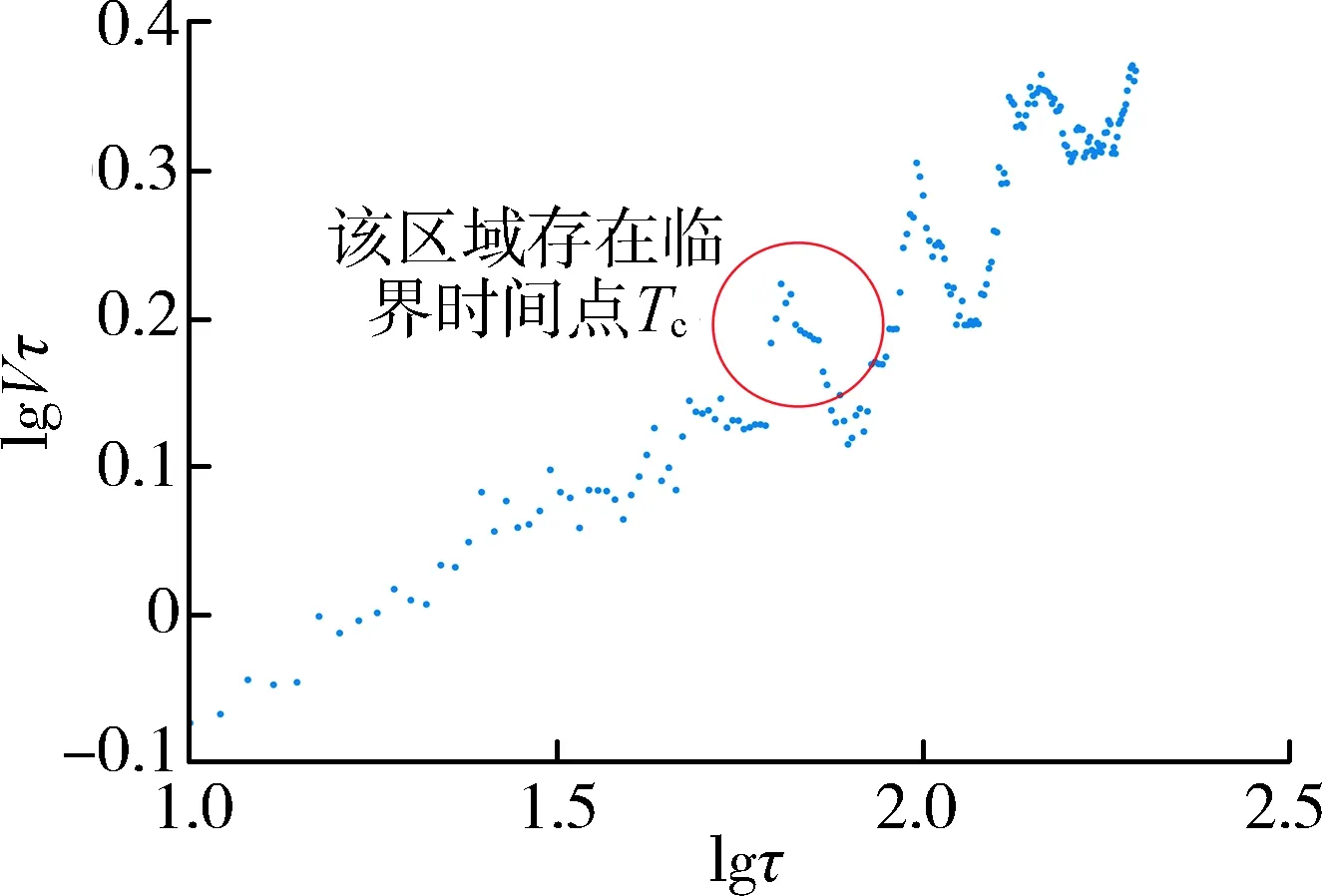
a.长程相关性判断。时间序列Hurst指数与分形维数D的关系为D=2-H。H和D的值有以下4种情况:当H=0.5,D=1.5时,表示该序列要素是随机的,即过去降水的状况与未来的趋势零相关;当0.5 b.长记忆性判断。在分形统计方法中,Vτ统计量定义为 (8) 由lgVτ-lgτ的图形判断时间序列的长记忆性程度。当该图形处于平坦直线段,说明该时间序列为独立的随机过程;当该图形处于向上倾斜曲线段,说明该时间序列具有长记忆性。从散点图的拐点横坐标确定临界时间Tc,可进一步推算该时间序列长记忆性的非周期循环长度T=10Tc。非周期循环长度为平均意义上的周期长度的周期,当样本数据足够大时,会在未来某个时刻以不同的长度进入下一个不同的周期。若lgVτ达到峰值后就趋于平坦,说明长记忆性过程开始扩散,时间序列趋于随机过程[18]。 根据以上理论分析,雨量预警指标阈值的求解模型建模步骤(图1)如下: a.对发生洪涝灾害24 h最大降雨时间序列进行雨量面平均处理,运用区域临界雨量法统计分析,得出初始临界雨量阈值[Rt临界,Rt]。 b.采用适线法对24 h最大降雨时间序列进行参数估计,并运用降雨灾害同频率法确定相应频率的雨量预警指标,将24 h最大雨量预警指标与初始临界雨量阈值对比并更新阈值[R′t临界,Rt]。 c.采用线性倾向估计法对降雨时间序列进行趋势分析,运用R/S分析法预测未来降雨趋势及非周期循环长度,利用雨量预警指标阈值实现在有效周期内预警。 图1 建模流程 江苏省泰兴市位于江苏省中部、长江下游北岸,以防洪区划由西向东划分为A、B区,如图2所示。气象资料显示,泰兴市年平均降水量1 043.2 mm,最大年降水量1 449.4 mm,最小年降水量462.1 mm;多年最大1 d暴雨降水量325.3 mm,最大降雨强度 80 mm/h,最大3 d降水量436.2 mm。降雨相关数据来源于江苏省泰兴市水务局提供的1981—2019年汛期(5月1日至9月30日)逐日降雨统计资料、中华人民共和国成立以来历史洪涝灾害资料以及《江苏省暴雨洪水图集》(1984年)。所采用的雨量站降雨数据具有良好的代表性、周期性和一致性[20],可用于相应的水文计算分析及趋势变化特征预测研究。 图2 泰兴市防洪区划 根据泰兴市1949年以来重大洪涝灾害事件情况,结合1981—2019年主汛期(6月1日至8月30日)逐日降雨记录资料,统计雨量站A1、A2、A3、B1、B2、B3站(以下简称“六站”)发生洪涝灾害的起止时间(此处以洪号为计)、单个洪涝场次24 h最大面平均雨量及对应的过程雨量,并计算各洪涝灾害场次24 h最大面平均雨量的均值(表1)。根据表1,以区域临界雨量法确定泰兴市洪涝灾害区域临界雨量阈值为92.75~116.42 mm,区域内任一雨量站 24 h 最大雨量值达到92.75 mm就可能激发洪涝灾害,需组织开展防洪防汛预警工作。 表1 泰兴市1981—2019年洪涝灾害区域24 h最大面平均雨量和过程雨量 表2 泰兴市不同频率不同时长最大面平均雨量 根据泰兴市分区特点,A、B区分别以A1、B1站为典型代表站,对比分析A、B区及泰兴市临界雨量指标。 a.统计泰兴市各雨量站年24 h最大雨量数据,计算年24 h最大面平均雨量,绘制、调试P-Ⅲ型曲线如图3所示,该时间序列均值为98.65 mm,用适线法拟合泰兴市年降水量经验频率点,得到最优拟合的P-Ⅲ型频率曲线,对应的Cs/Cv值为3.5、Cv值为0.39。1981—2019年泰兴市发生7次洪涝灾害,洪灾频率为17.9%,不同降雨频率下,泰兴市面平均雨量特征值如表2所示。为响应农村基层防汛预报预警体系建设,根据降雨与灾害同频率法,确定将泰兴市2年一遇洪水的临界面雨量指标作为防洪预警的依据,结合表1分析得出泰兴市临界雨量阈值为90.17~116.42 mm。 图3 泰兴市1981—2019年降雨频率曲线 b.统计A1、B1站的年24 h最大雨量数据,绘制、调试P-Ⅲ型曲线,该时间序列均值分别为105.39 mm(A1)、106.34 mm(B1),用适线法拟合两站年降水量经验频率点,得到最优拟合的P-Ⅲ型频率曲线,对应的Cs/Cv值皆为3.5,Cv值分别为0.34(A1)、0.33(B1);根据《江苏省暴雨洪水图集》短历时暴雨点面关系曲线,1 h、6 h、12 h、24 h最大雨量点面折算系数分别为0.855、0.905、0.915、0.925,以此确定A1、B1站辖区2年一遇洪水的临界雨量指标如表3所示,结合表1分析得出泰兴市临界雨量阈值为89.92~116.42 mm。 2.3.1降雨变化特征 a.月最大日降水量逐年变化趋势。以A1、B1站为代表雨量站,分别对A、B区进行降水量变化趋势分析。采用线性倾向估计法[21-22]研究泰兴市1981—2019年主汛期最大日降水量统计分布,如表4所示,A1、B1站6月最大日降水量都表现出下降趋势,下降速率分别为0.439 0 mm/a、0.750 5 mm/a;8月最大日降水量都表现出上升趋势,上升速率分别为0.275 8 mm/a、0.807 mm/a;两站7月最大日降水量变化趋势不同,A1站下降速率和B1站上升速率分别为0.236 8 mm/a、0.287 1 mm/a,其变化趋势如图4所示。 表3 A1、B1站2年一遇洪水临界雨量指标 (a) A1站 (b) B1站 表4 A1、B1站6—8月最大日降水量变化趋势 b.年最大日降水量逐年变化趋势。结合“六站”降雨资料,1981—2019年泰兴市最大日降水量逐年变化趋势如图5所示,最大日降水量有逐年上升趋势,上升速率为0.192 mm/a,确定性系数R2为0.013 6、最大日降水量平均值为98.65 mm。 图5 泰兴市年最大日降水量变化趋势 2.3.2未来降雨变化的趋势预测 统计分析泰兴市代表雨量站A1、B1站汛期月最大日降水量变化特征及泰兴市年最大日降水量变化特征,进一步研究最大日降水量的周期性,即研究最大日降水量是否具有规律性。利用Matlab软件分别对A1、B1站汛期月最大日降水量数据、泰兴市年最大日降水量数据进行R/S分析、统计量分析得到 lg(R/S)-lgτ、lgVτ-lgτ的关系,如图6和图7所示。在lgVτ-lgτ散点图上找到趋势开始发生变化的拐点或转折点,该点横坐标对应的时间为该时序的临界时间TC,即可确定T值。对lg(R/S)-lgτ关系图用式(7)进行最小二乘拟合,进一步求得Hurst指数、分维数、回归系数及其他统计量,如表5所示。 a.泰兴市发生洪涝灾害区域临界雨量阈值为89.92~116.42 mm,表明降雨灾害同频率法可精细化雨量阈值,为农村基层防洪防汛提供参考。 b.泰兴市年最大日降水量表现出上升趋势,A1站8月和B1站7月、8月最大日降水量表现出不同程度的上升趋势,A1站6月、7月和B1站6月最大日降水量表现出不同程度的下降趋势。由表5可知,0.5 (a) A1站R/S分析 (b) A1站统计量分析 (c) B1站R/S分析 (d) B1站统计量分析 (a) R/S分析 (b) 统计量分析 表5 泰兴市、A1站、B1站最大日降水量变化趋势预测统计量 本文以江苏省泰兴市为例,以降雨资料时间序列分析为基础,结合区域临界雨量法、降雨灾害同频率法、R/S分析法等3种分析方法构建了雨量预警指标阈值求解模型。检验结果显示,此模型可精细化雨量阈值并使其在周期内有效预警,可用于研究区乃至平原区洪涝预警。求解模型可为平原区农村基层洪涝灾害的特征分析、评估和监测提供参考,且能对未来降雨变化进行预测、预警。1.4 求解模型建立
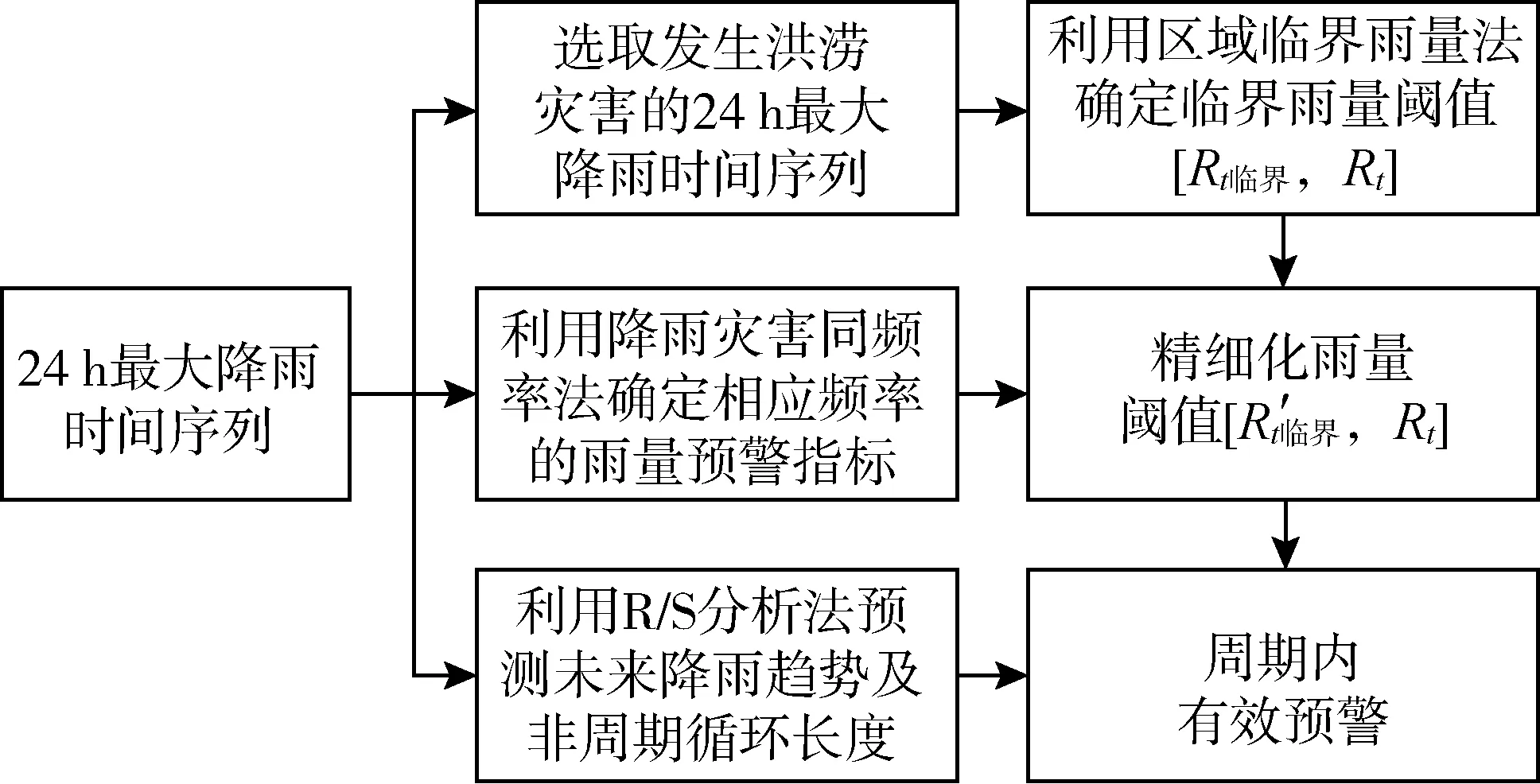
2 实例验证
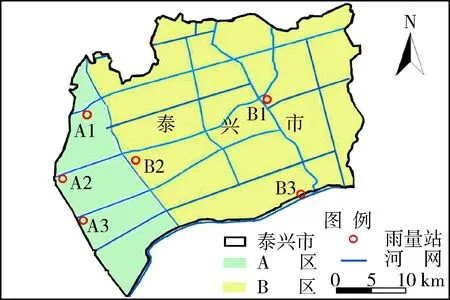
2.1 区域临界雨量阈值


2.2 临界雨量指标

2.3 趋势分析


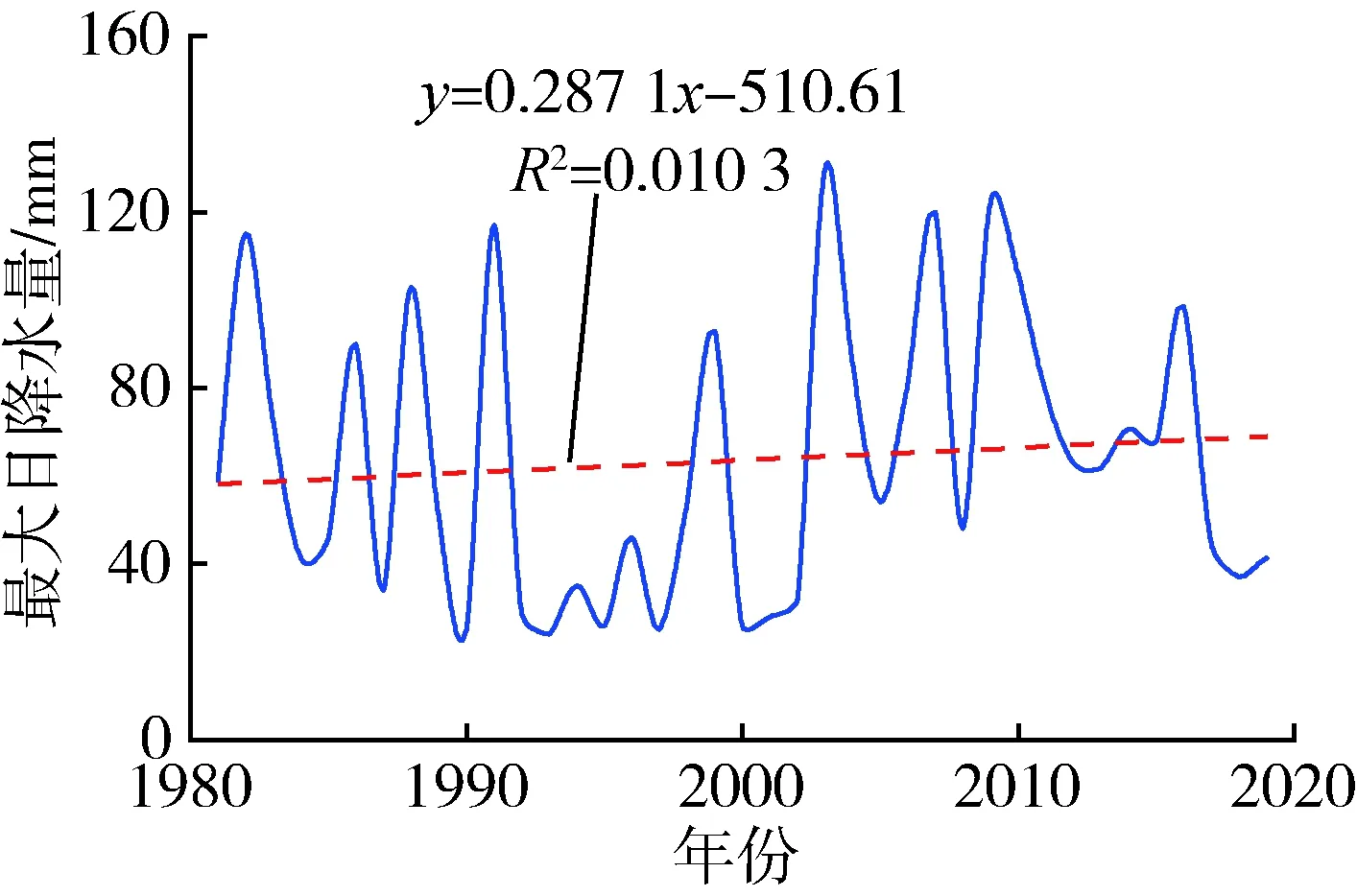

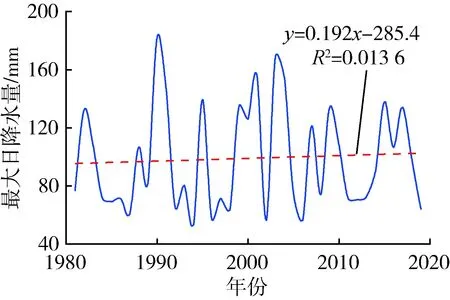
2.4 结果分析
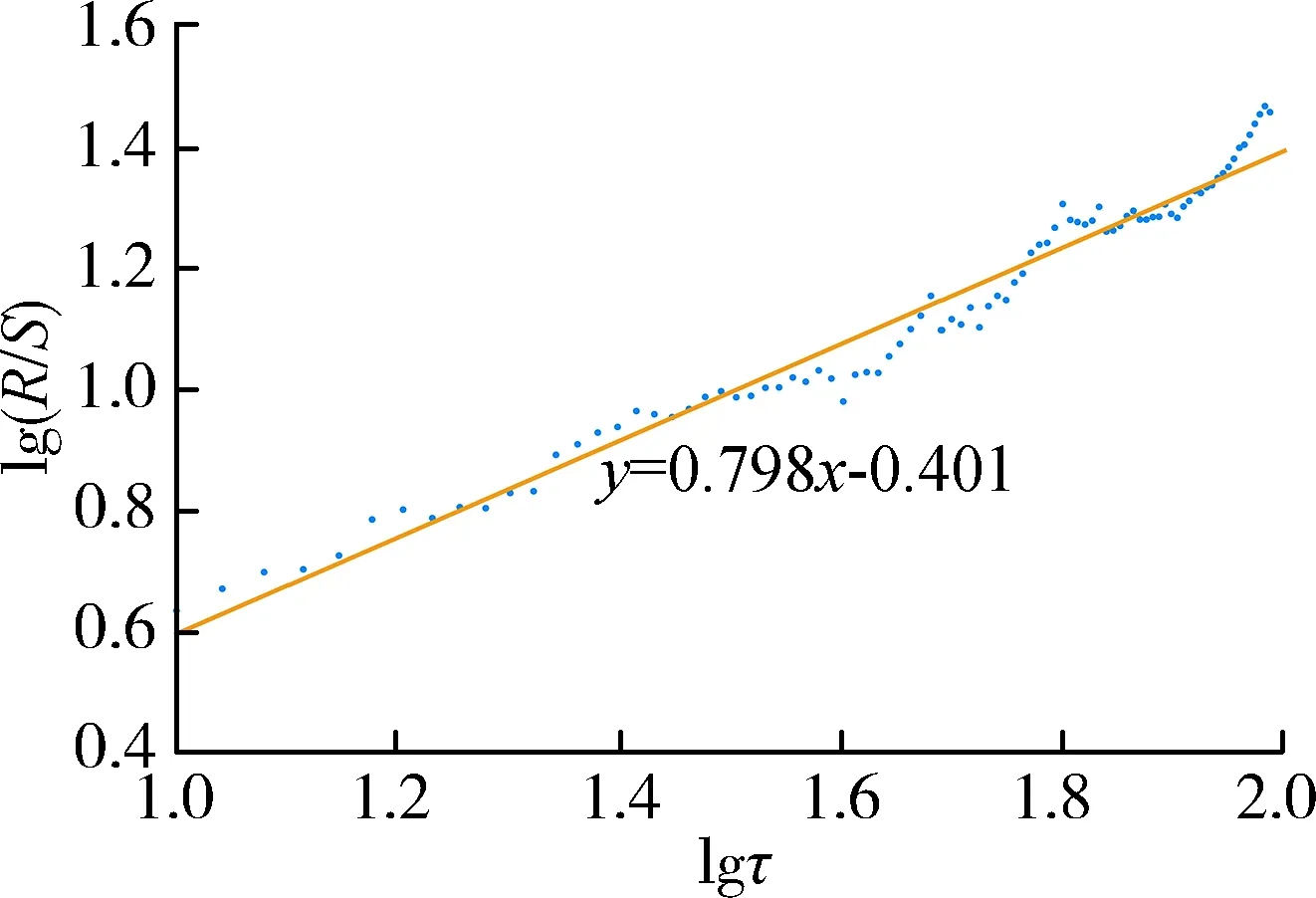
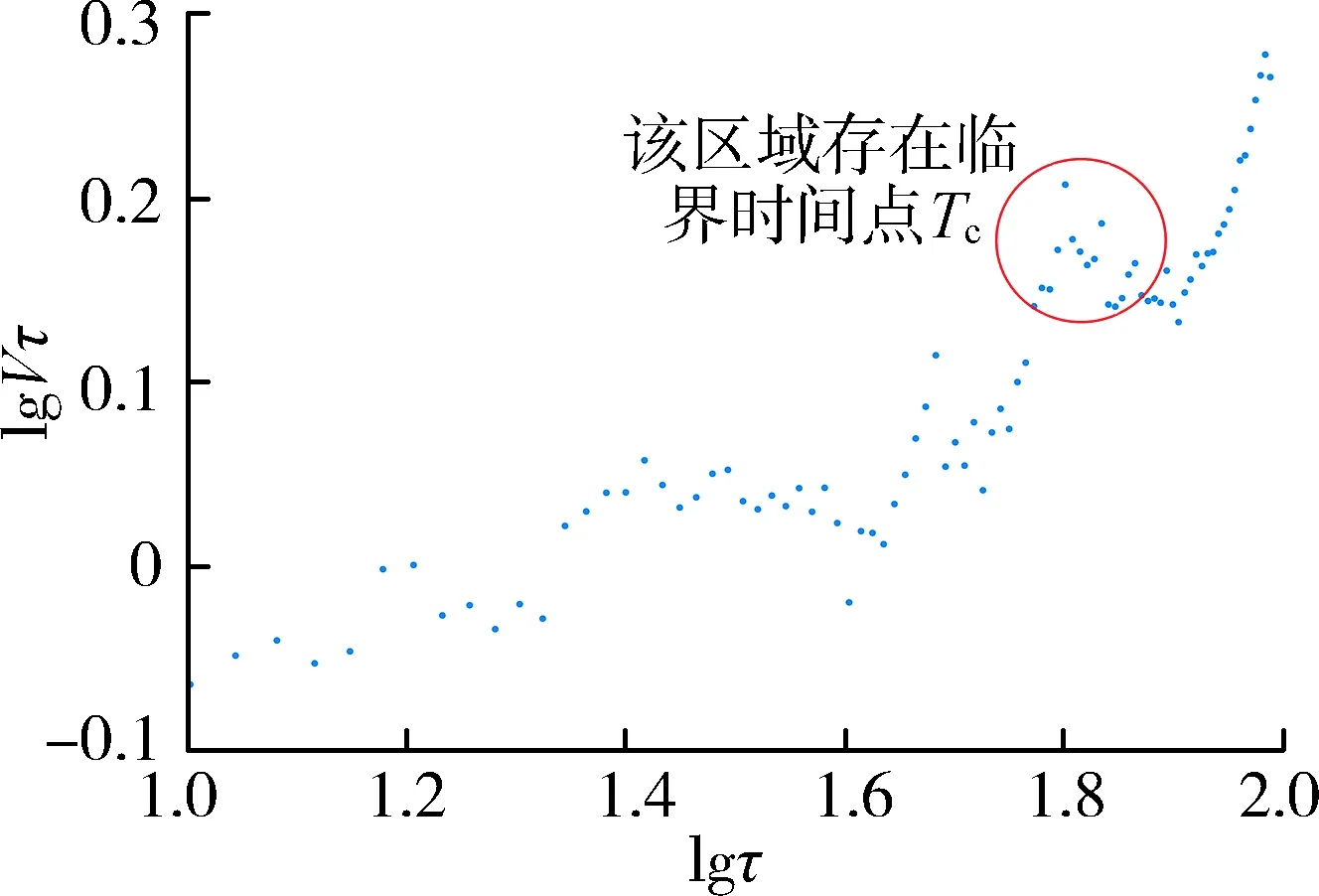
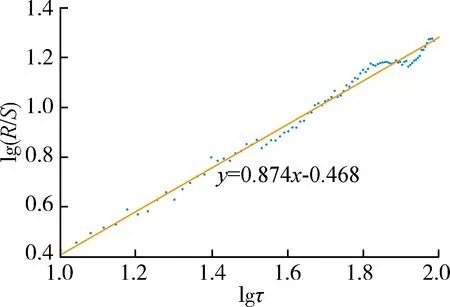


3 结 语
