(2+1)维Sawada-Kotera方程的黎曼theta函数周期波解及渐近性质

房春梅

(集宁师范学院 数学与统计学院，内蒙古 乌兰察布 012000)

非线性微分方程在非线性科学中的作用越来越明显,特别是解析解的构造.目前,在几代专家的不断努力下,发展了大量构造微分方程解析解的有效方法[1-5].Nakamura利用黎曼 theta函数的拟周期性和Hirota直接法提出了一种求非线性微分方程拟周期波解的简单方法[6].范恩贵和田守富等人将此方法进行改进并求得了很多微分方程的周期波解[7-10].此外,近期人们得到了(3+1)维爆破孤子方程[11]、Boussinesq方程[12]、耦合双线性方程[13]、Toda-型方程[14]等的N周期波解.

(2+1)维Sawada-Kotera方程(SK)方程[15]为如下所示:

它是著名的刘维尔场论的守恒流方程,广泛应用于亚临界弦,二维量子引力规范场论,共形场论和非线性科学等物理分支.对于SK方程,文献[16]利用τ函数获得了贝克隆变换和Lax对,其行波解[17]、呼吸波解[18]、lump解和共振条状孤子解[19]、Painleve性质[20]、新的双线性贝克隆变换[21]、多孤子解[22]、初边值问题与darboux-levi型变换[23]以及一些其它孤波解被成功地获得[24-27].但其黎曼theta函数周期波解还没有得到.该文构造了SK方程的双线性表示,孤子解和黎曼theta函数周期波解,并给出了周期波解和孤子解之间的关系.

1 (2+1)维SK方程的双线性形式和孤子解

这一节,构造了SK方程的双线性形式和孤子解,下面简要介绍如何利用Bell多项式得到方程(1)的双线性表示式.为了找到式(1)的双线性表示式,引入以下变换:

u=c(t)qxx,

(2)

其中c(t)是一个待定函数.将变换式(2)代入式(1),得到：

对式(3)关于x积分一次变成：

5c(t)2q2xq4x-5c(t)2q2xqx,y+5c(t)q2y-δ=0,

(4)

其中δ是一个积分常数.假设c(t)=1则方程(4)变为

利用P-多项式,等式(5)可以表示为

E(q)=Px,t(q)-P6x(q)+5P2y(q)-5P3x,y(q)-δ=0.

(6)

根据贝尔多项式的相关性质,并进行如下变换：

q=2(lnf)↔u=c(t)q2x=2(lnf)xx.

(7)

可得到SK方程的双线性表示式为如下所示：

接下来,将利用SK方程(1)的双线性表示式构造它的N阶孤子解.在式(8)中令δ=0,并假设f可以按参数ε展开成级数为

根据Hirota直接法,结合双线性表示式(8)和式(9),通过计算很容易得到式(1)式的N阶孤子解为

其中：

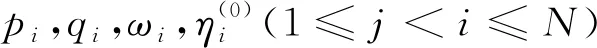
当N=1时,得到SK方程的一阶孤子解为

u=2[ln(1+eη)]xx.

(12)

其中:

η=px+qy+ωt+η(0),ω=p5+5p2q-5q2p-1.

当N=2时,二阶孤子解为

u=2[ln(1+eη1+eη2+eη1+η2+A12)]xx.

(13)

其中:

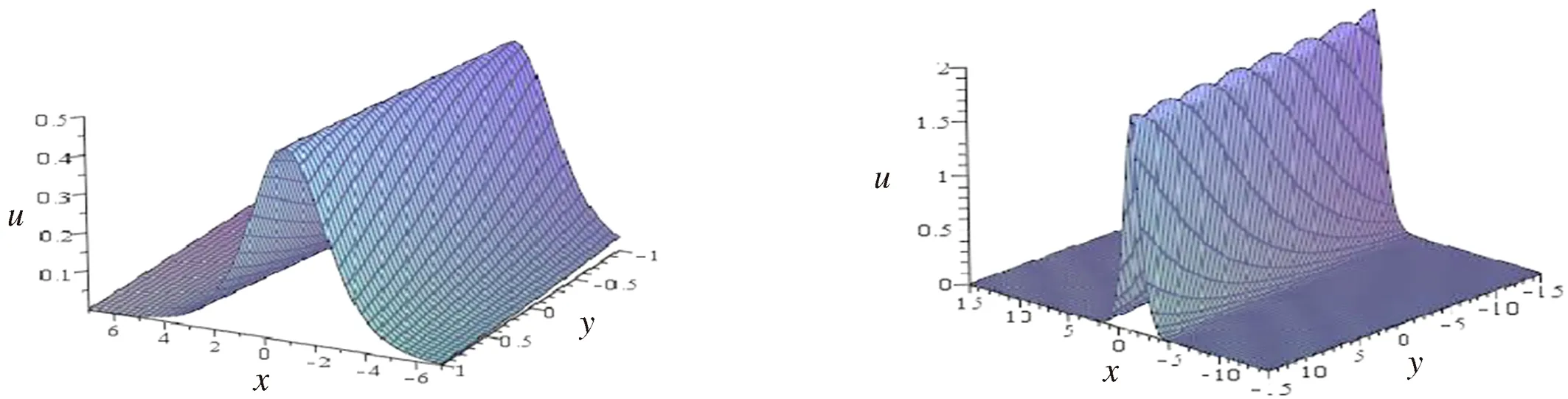
(2+1)维SK方程的一阶和二阶孤立波解的空间传播图如图1和图2所示.

2 (2+1)-维 SK方程的周期波解

在文献[8]的基础上,获得SK方程的黎曼theta函数周期波解.黎曼theta函数定义为

其中n=(n1,n2,…,nN)T∈ZN是N阶整数值向量，ξ=(ξ1,ξ2,…,ξN)T∈CN是N阶复相位变量.特别地,令N=1时,黎曼theta函数为

其中相位变量ξ=kx1+lx2+…+ρxN+ωt+ε,且Im(τ)>0.

当N=2时,黎曼theta函数表示为

其中变量ξi=kix1+lix2+…+ρixN+ωit+εi,i=1,2,n=(n1,n2)T∈Z2,ξ=(ξ1,ξ2)∈C2,且-iτ是一个实值正定对称2×2矩阵，表示为

定理1设ϑ(ξ,τ)是N=1,ξ=kx+ly+ωt+ε时的黎曼theta函数,则SK方程的一阶周期波解为

(18)

其中:

且

其中k,ε,τ为自由参数.

结合式(21)和式(8),可以得到以下结果:

20(2n-1)2π2l2,+δ)eπi(2n2-2n+1)τ=0.

(22)

根据表达式(20)、等式(22)可以重写为如下形式:

解上述方程组,可得到方程(1)的周期波解为

(24)

其中ϑ(ξ,τ)由式(15)给出，k,ε,τ是自由参数.

类似于上述求一阶周期波解的过程,可以得到关于二阶周期波解的如下定理.

在原有通信实训室基础之上，新建移动无线网络优化中心。以移动无线网络优化为主要建设内容。学员可通过各种网络优化工具进行系统采集移动无线网络数据、定点路测数据、数据分析及优化等实训，实训场地及设备按照企业生产经营要求设置，形成真实的职业环境。

定理2设ϑ(ξ,τ)是N=2,ξi=kix+liy+ωit+εi,i=1,2,时的黎曼theta函数,则SK方程的二阶周期波解为

(25)

其中参数ω1,ω2,u0,δ满足下面关系式：

H(ω1,ω2,u0,δ)T=b,

(26)

而且

H=(hij)4×4,b=(b1,b2,b3,b4)T,

(27)

证明根据文献[8]中的定理2,参数ki,li,ωi和εi满足下面的方程组:

下面引入以下变换来构造SK方程的更一般的双线性形式,设:

将上式代入式(1)中并关于x积分一次,可以很容易地得到SK方程更广义的双线性表示式为

此外,根据式(28)以及广义双线性形式,可以得到下面的4个等式:

80π4〈2n-θi,k〉3〈2n-θi,l〉-20π2〈2n-θi,l〉2+δ)×eπi[〈τ(n-θi),(n-θi)+(τn,n)〉]=0,

(30)

根据表达式(27),上面的方程组可以改写为

解式(31),可以得到方程(1)的以下二阶周期波解:

(32)

其中ϑ(ξ1,ξ2)由式(16)给出,ki,li,εi和τij是任意参数.

(2+1)维SK方程的一阶周期波解在参数k=0.2,l=0.3,τ=2i,ε=0以及二阶周期波解在参数k1=0.01,k2=0.3,l1=0.1,l2=-2,τ11=i,τ22=2i,ε1=ε2=0下的空间传播图如图3和图4所示.

3 渐近分析

下面将给出关于一阶周期波解渐近性质的定理及其详细证明.

定理3假设(ω,δ)是方程组(23)的解,在一阶周期波解式(18)中令

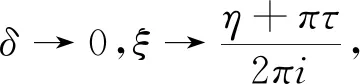
(34)

(35)

再利用文献[8]中的公式(4.10)和(4.12),可以得到:

由文献[8]中的命题3,进一步可以得到:

再根据文献[8]中的(4.11)式,能得出:

(38)

δ→0,2πiω→p5+5p2q-5q2p-1.

(39)

为给出渐近关系,将周期函数ϑ(ξ)展开成如下形式:

(40)

(41)

ϑ(ξ,τ)→1+eη.

(43)

4 结论

该文得到了SK方程(1)的两类解,即N阶孤子解(10)和黎曼theta函数解(18)、(25).从文中可以看出,非线性微分方程一旦写成双线性形式,就可以分别用Hirota直接法和Hirota-黎曼theta函数相结合得到其孤子解和黎曼theta函数周期波解.孤子解和黎曼theta函数解之间似乎没有什么联系,但是从定理3可以看出,黎曼theta函数周期波解在某些极限条件下趋向于对应的孤子解.