饱和重塑黏性土一维固结状态下应变率效应的经验模型研究
2021-12-04郑娟伍肖赖秀英
郑娟,伍肖,赖秀英
(1 莆田学院土木工程学院,福建 莆田 351100;2 台州市交通勘察设计院,浙江 台州 318000)
黏性土一般具有比较明显的变形的时效性,因此建立正确体现土体应力应变与时间关系的本构模型,一直是岩土力学一个重要的研究方向。国内外学者对土体应变的时效性虽取得了一些研究结果,但仍存在分歧,有些学者认为土体应力应变与时间的唯一性关系只存在于无明显孔压的次固结阶段,而在主固结阶段不成立[1-2],有些学者认为存在孔压消散的主固结阶段,土体的应力应变与应变速率具有唯一性关系[3~5],且基于该理论建立的模型属于率相关本构模型。
目前,国内关于应变加载速率对岩石[6~12]、冻土[13]及砂土类[14]土体性质影响的研究较多,国外虽有学者专项研究黏性土的应变率效应[15~17],然而基于主次固结耦合思想建立的应变率效应模型却仍然有限,因此,本文选取西安北郊某深基坑原状土进行重塑饱和,对其进行单轴恒定应变率(CRS)固结试验,考察不同加载速率条件下土样应变的率相关特性,并借此响应建立时间隐式率相关的经验本构模型,从而为饱和重塑黏性土单轴状态下应变率效应模型的建立得到一定的理论依据。
1 饱和重塑黏性土的单轴CRS固结试验
1.1 土样及试验方法
试验所用土样取自西安北郊某深基坑现场,原状土液限wL为28.8%,塑限wP为16.9%,塑性指数IP为11.9>10。将原状土风干碾碎过0.5 mm筛后测定其含水率,并按30%的含水率配备土样,闷料24 h后通过控制干密度重塑成样,最后采用真空饱和法确保试样饱和度超过98%。
本单轴CRS固结试验采用自行改制的固结容器,改制的主要部分包括侧向孔压及测定装置、底部孔压及测定装置、排气孔以及透水石,其中侧向及底部传感测定装置能弥补常规单轴固结试验无法准确量测侧压及底部孔压的缺陷,带凹槽钢网贴面的钢制透水石在保证排水通畅的情况下减弱了透水石因自身变形引起的试验误差。制备好的饱和重塑黏性土采用该K0固结容器进行连续加载,加载过程控制应变变化率为定值。
在单轴CRS固结试验中,选取合适的试验应变率是试验方案成功的关键。这是因为过小的应变率会导致试验用时过长,进而易导致土体温度等发生变化而产生自胶结,而且过小的应变率不易控制,易使试验出现较大的误差;过大的应变率在某类土中会致使土体变形严重滞后,且热量无法消散,进而使得试验数据不准确。较为合理的应变率应满足LEE K等[18]得出的无量纲参数χ小于0.1时试验结果才能较有效反映土体单轴K0固结的应变率效应,计算公式为
(1)
本文加载速率在参考实际常见施工速度的基础上进行了一定速率范围的拓展,将连续施工与分段施工分别用加载速率的快慢来体现,鉴于此试验设定加载速率范围为0.9~55.4%/h。在土样加载过程中,排水阀门始终开启,并借助位于试样底部的传感器测定孔压。试验土样均加载至设定的最大轴向应力1 MPa,整理数据,获得共计55组较为完整的土样试验数据。
1.2 试验结果与分析
整理试验数据时发现应力应变的半对数坐标中出现了较为一致的曲线特征,因此,为了更清晰显现出试验曲线的特征,只选择部分代表性速率绘制图,结果(图1)显示:不同加载速率的土样均出现前段平缓后段陡峭的曲线特征。同时,曲线整体体现为竖向应变随竖向应力增长而增大,最终达到1 MPa时,加载速率越快对应产生的应变值越小。对照曲线形状特征作进一步分析发现,加载较慢曲线较为陡峭,说明加载过程中的排水使得孔压减小,因而应变与应力较为同步;加载较快曲线则比较平缓,体现了孔压积聚阻碍了应变的发生,使得变形滞后于应力。在后续试验中发现,加载结束后若保持应力不变,则土体变形会继续发展,说明该土样具有蠕变特性,也正是应变滞后的体现,进一步说明了试验数据的可信性。ε1—logσv关系曲线直观体现了加载应变率的影响,下文将针对不同加载速率的土样进行回归分析,以期建立数理化公式。
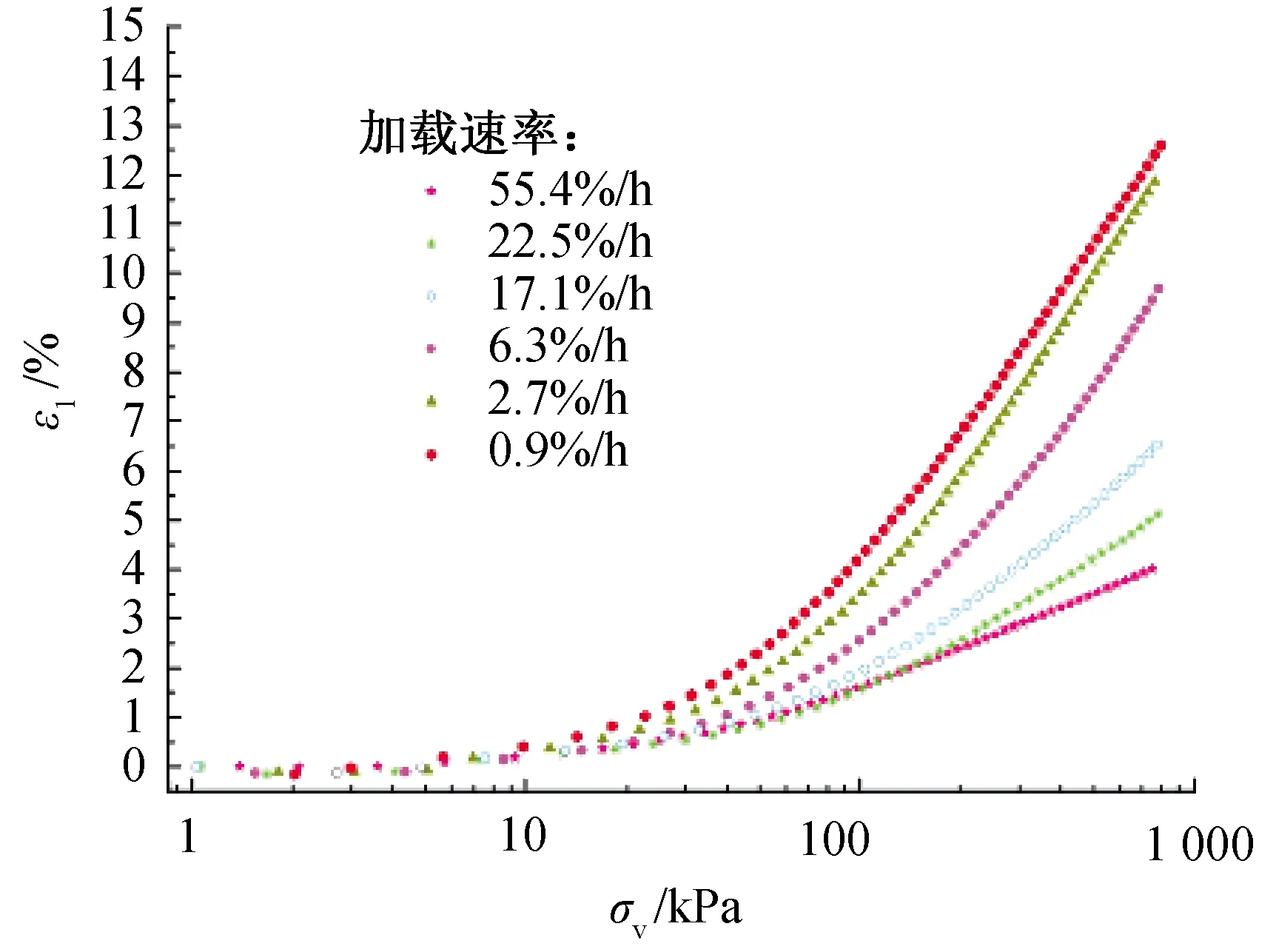
图1 ε1—logσv关系曲线
2 表观固结阻力的应变率效应
2.1 表观固结阻力的提出
基于图1显现的曲线特征,合理推断每条曲线都存在一个最大曲率点,在该点前后ε1—logσv关系曲线特征发生较大的变化,即理论上最大曲率点是该曲线的拐点。在数据回归分析中发现该点具有一定的物理意义,故本文将ε1—logσv曲线上曲率最大点所对应的竖向应力σv定义为土体的表观固结阻力σp,其物理意义是土样克服仪器侧壁摩擦力与其结构应力的合力。无论原状土还是室内重塑土都不可避免地处于地球的重力场中,不可能达到完全随机的排列及颗粒间相互完全独立无联系,因而总是表现出一定的结构性[19]。排除偶然误差的影响,每个土样的该应力值应是一样的,不会随加荷速率的不同而不同,但是土样与仪器侧壁存在的摩擦力会随着加荷速率的不同而呈现与加载速率正相关的单向变化趋势,所以根据土样克服仪器侧壁摩擦力与其结构应力的合力σp对土样排水固结产生了一定的阻碍,将其定义为表观固结阻力。
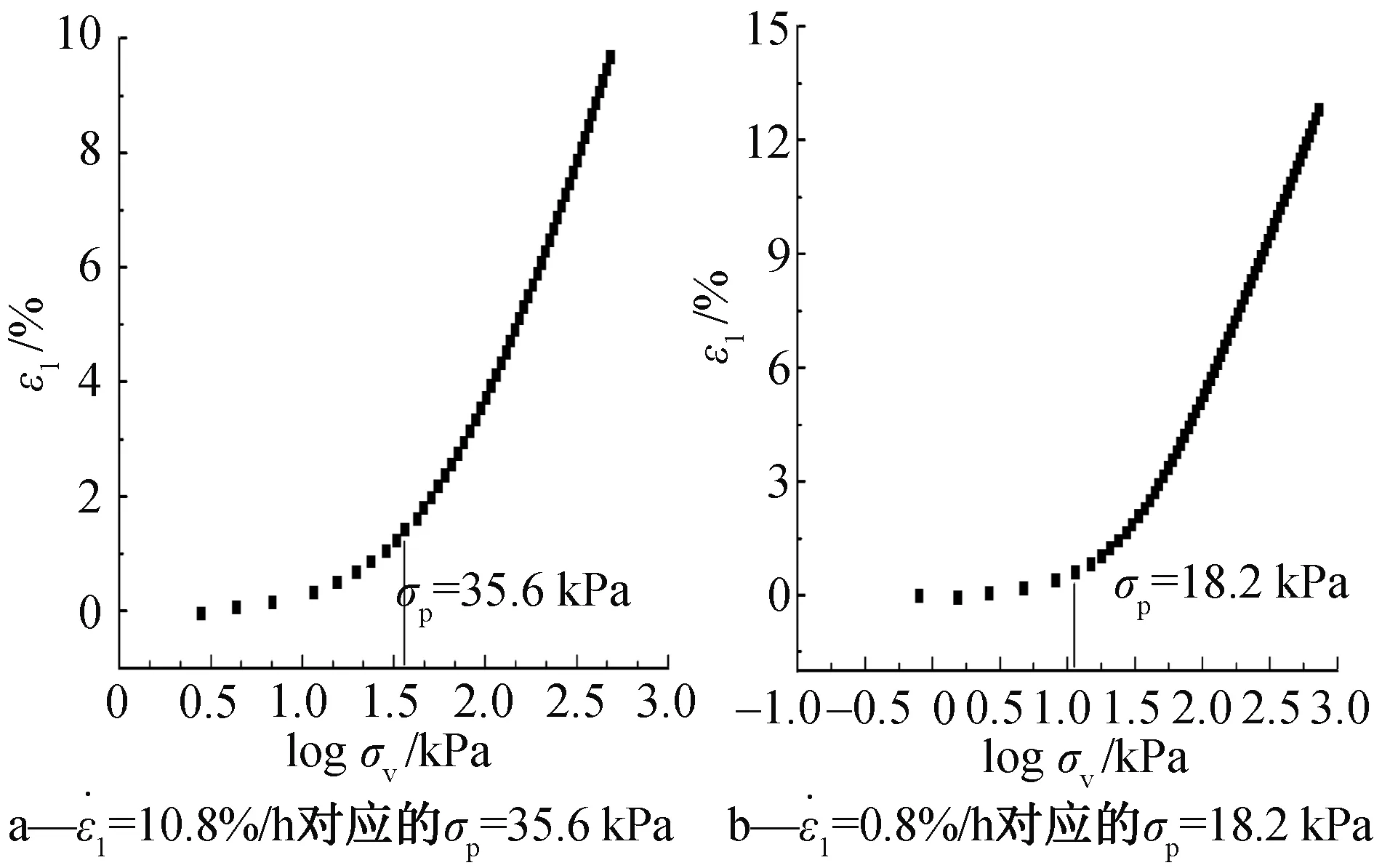
图2 不同加载应变速率对应的σp值
进一步分析可知:以表观固结阻力σp为界,在土体轴向应力σv小于该值时不同加载速率土样的曲线几乎重合,说明该段无明显的应变率效应;当土体的轴向应力σv大于该值后,应变率效应表现明显,试验控制的加载应变率越大对应的轴向应力值越高,且这种应变率效应在整个固结过程中持续体现。
2.2 应力应变曲线的速率归一特性
借助表观固结阻力σp对不同加载速率土样进行归一处理,归一后的曲线关系(图3)显示:不同加载速率土样的应力应变关系曲线基本重合,并体现出良好的函数关系。
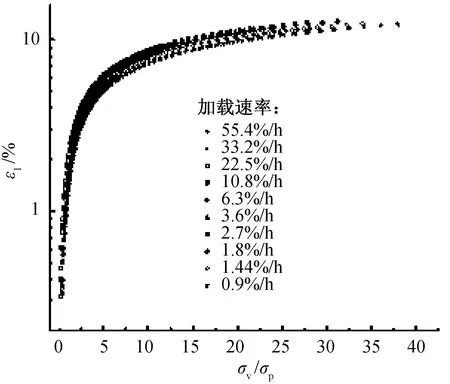
图3 归一后的试验曲线
对其进行拟合,曲线特征符合函数规律y=m(1-nx),即
ε1=m(1-nσv/σp),
(2)
式(2)中m、n为拟合参数。当σv=0时,nx→1,则ε1=0,表示试验开始的一瞬间状态;当σv→∞时,nx→0,则ε1=m,m表示无限加载对应的应变值,对于某一土体的K0状态而言为一无限趋近的定值。假设σv=σp时对应的应变为εp,则n=(m-εp)/m,表示有应变率效应部分产生的应变值占总应变值的比例,可借助n描述应变率效应对土体变形的影响程度。
图4中实线为数据拟合曲线,拟合相关度很高,说明该土体的一维压缩曲线的率相关性可由其表观固结阻力σp的应变率效应来描述。
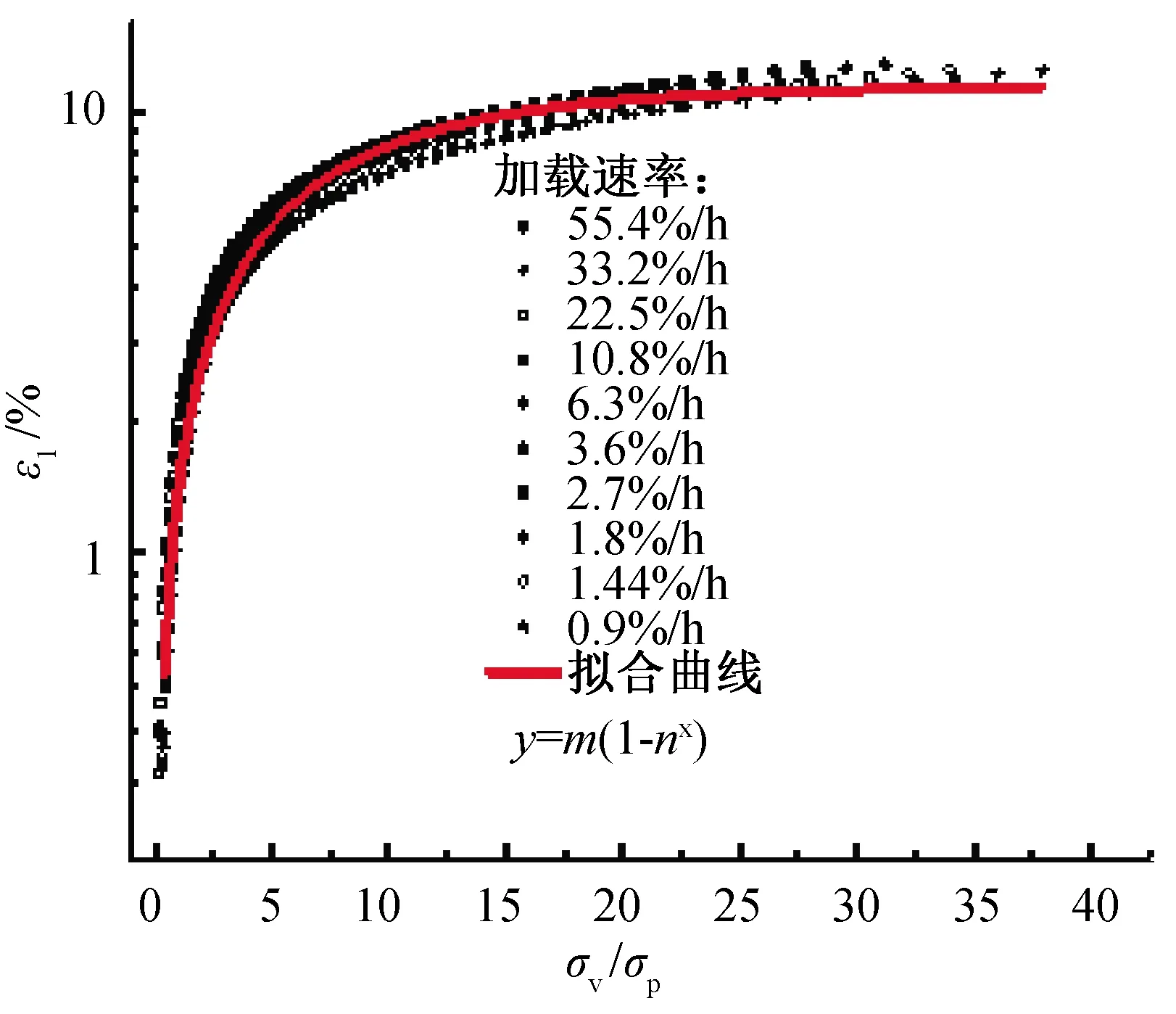
图4 归一化后的应力应变曲线的拟合
如前文分析,表观固结阻力σp值的应变率效应呈现单向变化趋势,借用GRAHAM J等[20]定义的一个无量纲应变率参数来描述其应变率效应。GRAHAM J等[20]所用参数为η0.1,用于表示单轴CRS固结试验中,以加载速率为0.1%/h对应的先期固结压力为基准值,在加载速率增大10倍时对先期固结压力的影响。基于此,根据本文定义的各参数符号将表达式改为更通用的方程如下:
(3)
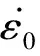
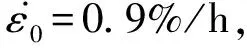
3 表观固结阻力σp的应变率效应模型
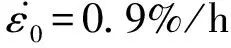
(4)
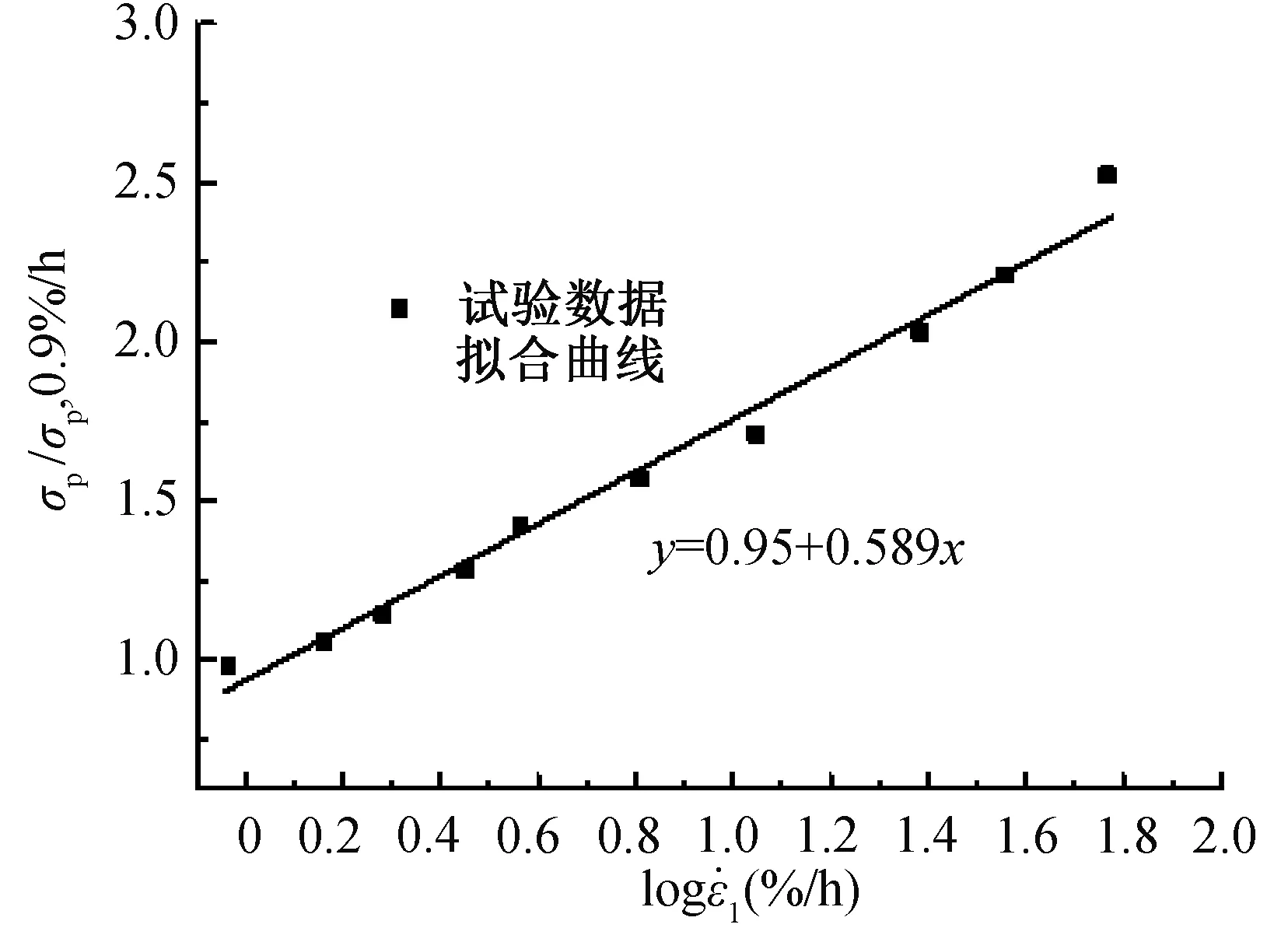
图关系曲线
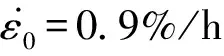
(5)
式(5)中m、n、A、B均为拟合参数,代表一定的物理意义,m表示无限加载对应的应变值,n表示固结过程中有应变率效应部分产生的应变值占总应变值的比例。
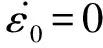
本文采用的单轴CRS固结试验为单轴侧限恒定应变率固结试验,一般多适用于室内实验研究。考虑到目前实验室的常用加压设备对于应变控制的稳定性一般高于对应力的控制,基于该固结试验数据建立的模型更利于基本原理的发现。
4 结论
本文通过设计单轴恒定应变率固结试验,对取自西安北郊某深基坑土样的应变率效应进行了研究,得出了以下结论:
(1)根据整理试验数据过程中发现的前平缓后陡峭的曲线规律,合理推断曲线存在拐点,并将曲线拐点对应的应力值σv定义为表观固结阻力σp。