高地隙自走式喷雾机横向稳定性滑模控制的研究
2021-12-04张鹏冯静安宋宝喻俊志
张鹏,冯静安*,宋宝,喻俊志
(1 石河子大学机械电气工程学院,新疆 石河子832003;2 华中科技大学机械科学与工程学院,湖北 武汉 430074;3 中国科学院自动化研究所复杂系统管理与控制国家重点实验室,北京 100190)
高地隙自走式喷雾机属于特种作业车辆,驱动力控制的相关研究主要是以驱动力防滑控制为研究出发点[1]。关于这类作业车辆横向稳定性的研究较少,主要研究接近于汽车工程领域。其相关的控制方法主要有经典的 PID 控制、滑模控制、模糊控制等[2],其中PID控制及其衍生的各种控制方法已经相当成熟[3-4],滑模控制[5-7]方法因能克服非线性系统不确定性的优点而被广大学者采用。
本文针对高地隙自走式喷雾机操纵稳定性控制效果差的问题,着眼于控制系统的理论研究,设计了以车身横摆角速度和质心侧偏角为参数输入量、车轮驱动力矩为输出量的整车力矩控制器,考虑到轮毂电机力矩改变的瞬时性,通过适时改变车轮驱动力矩,主动干预车辆行驶状态的方法,以实现附加横摆力矩来控制车辆行驶轨迹,提高车辆的主动安全性能,最后基于Matlab/Simulink平台建立系统仿真模型,进行典型工况下整车力矩控制器控制效果仿真试验验证和分析评价。
1 高地隙自走式喷雾机模型建立
本文研究的高地自走式隙喷雾机主要由车轮、悬架、车体、药箱、喷杆及电子电气6个部分组成(图1),为了研究方便,本文忽略悬架弹簧阻尼特性,认为车轮和车架之间刚性连接;控制系统验证过程时间较短,可以认为短时间内负载质量一定,整车和负载总质量用M表示;不考虑喷杆对车辆操作稳定性的影响。
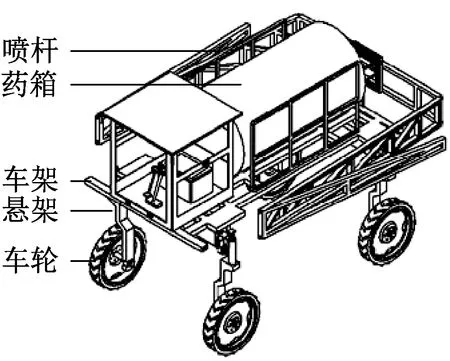
图1 高地隙自走式喷雾机
1.1 整车模型的建立
为了便于研究高地隙自走式喷雾机在低速工作时车辆操纵稳定性控制,考虑车身纵向运动、侧向运动、横摆运动和四轮旋转运动的七自由度非线性车辆模型,建立以车辆前进方向为x轴、侧向运动为y轴、质心为坐标原点的直角坐标系xoy(图2)。其纵向运动方程为
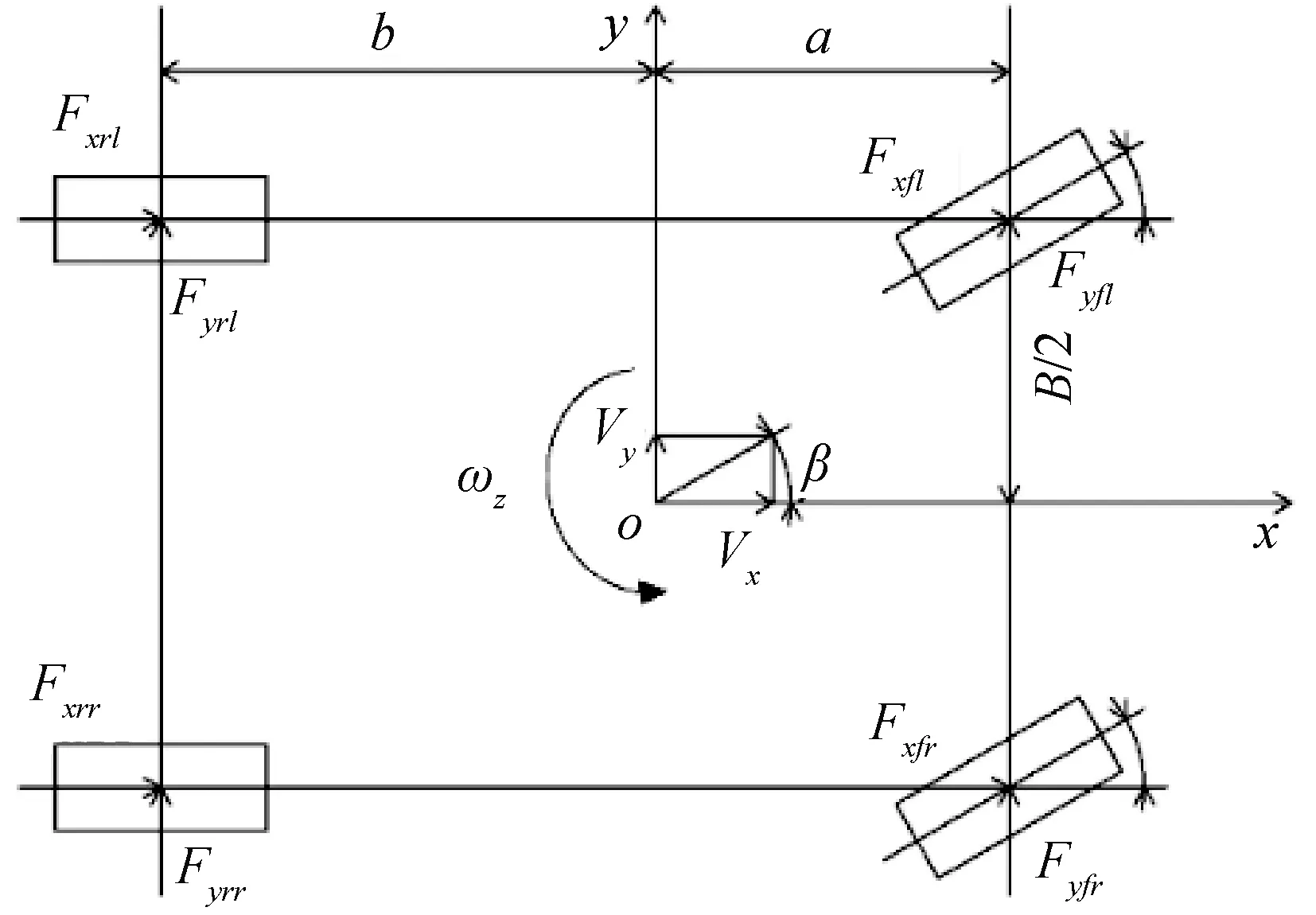
图2 整车受力分析
(1)
横向运动方程为
(2)
横摆运动方程为
(3)
上式中M为整车质量,kg;a、b分别是质心到前轴和后轴的距离,m;d表示轮距,m;δi为车轮转角,rad;Fyi、Fxi分别为轮胎在车身坐标系下所受的侧向力和径向力,N(下标i为fl、fr、rl、rr分别表示左前、右前、左后、右后的车轮);Vx、Vy分别是沿着坐标轴x和坐标轴y整车纵向和侧向速度,m/s;Iz表示车身绕质心垂向旋转的惯性质量,kg·m2;ωz为横摆角速度,rad/s。
车轮转动方程为
(4)
式(4)中Ji为车轮转动惯量,kg·m2;ωi为车轮转速,rad/s;Tei和Tbi分别为车轮转矩和制动力矩,N·m;R为有效转动半径,m。
1.2 轮胎模型
轮胎模型有统一轮胎模型、Pacejka 魔术公式[8]模型、Dugoff轮胎模型[9]等。本文采用Dugoff轮胎模型,该模型依据假定轮胎与接触点成矩形,通过综合考虑轮胎刚度、滑移率等参数适合用于车辆动力学算法控制的研究,计算公式如下:
(5)
(6)
(7)
(8)
上式中Fl、Fc是车轮纵向和横向受力,N;α为轮胎侧偏角,rad;kx和ky分别为轮胎纵向刚度和侧向刚度;s为滑移率;μ为摩擦系数;R为轮胎半径,m;H为无量纲参数。
轮胎受力和车身坐标下轮胎力的关系如图3所示,数学关系如下:
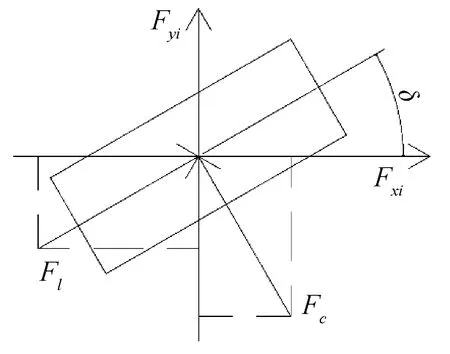
图3 车轮受力分析
(9)
对于后轮受力关系而言,相当于前轮转角为0的情况。
1.3 理想模型
假设车辆转弯行驶过程中,纵向速度保持不变,侧向加速度小于0.4 g,轮胎侧偏特性处于线性范围,从而忽略车辆侧倾、俯仰、纵向和垂向运动后,可简化成整车二自由度车辆模型[10],将质心侧偏角和横摆角速度作为理想模型的状态变量,车辆状态空间方程如下:
[βzd,ωzd]T=E[βzd,ωzd]T,
(10)
式(10)中
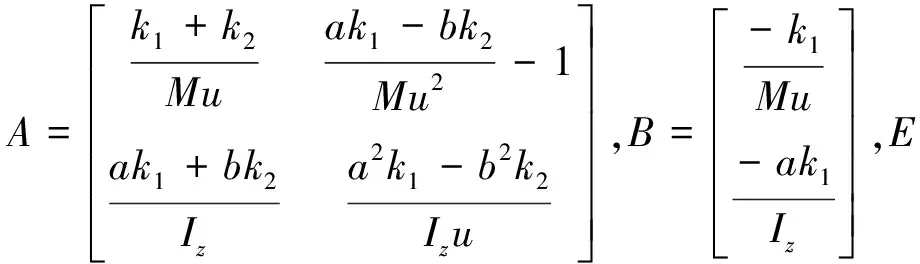
(1)质心侧偏角期望值的确定。传统车辆理想的质心侧偏角应当始终为0,但是质心侧偏角始终为0,将严重影响低速作业车辆的转向性能。充分考虑到高地隙作业车辆低速作业过程,取质心侧偏角的极限值为±10°,其表达式如下:
sign(δ),
(11)
(12)
2 整车力矩控制器设计
2.1 控制系统原理设计
本文车辆车轮的驱动力矩Tei由两部分构成,分别是维持车辆正常运行的行进力矩Ti和维持车辆横向稳定性的驱动力矩ΔT,即车辆车轮的驱动力矩计算公式为:
Tei=Ti+ΔTi
(13)
式(13)中Ti是维持车辆前进的行进力矩,其控制原理依据车辆行驶速度和目标行驶速度之间的差值通过PID控制计算出控制量,再将其分配给4个车轮,同轴2个车轮的控制力矩大小相等,前后轴车轮按照车辆质心分布位置确定;ΔTi是附加横摆力矩执行机构依据附加横摆力矩分配给车轮的驱动力矩。
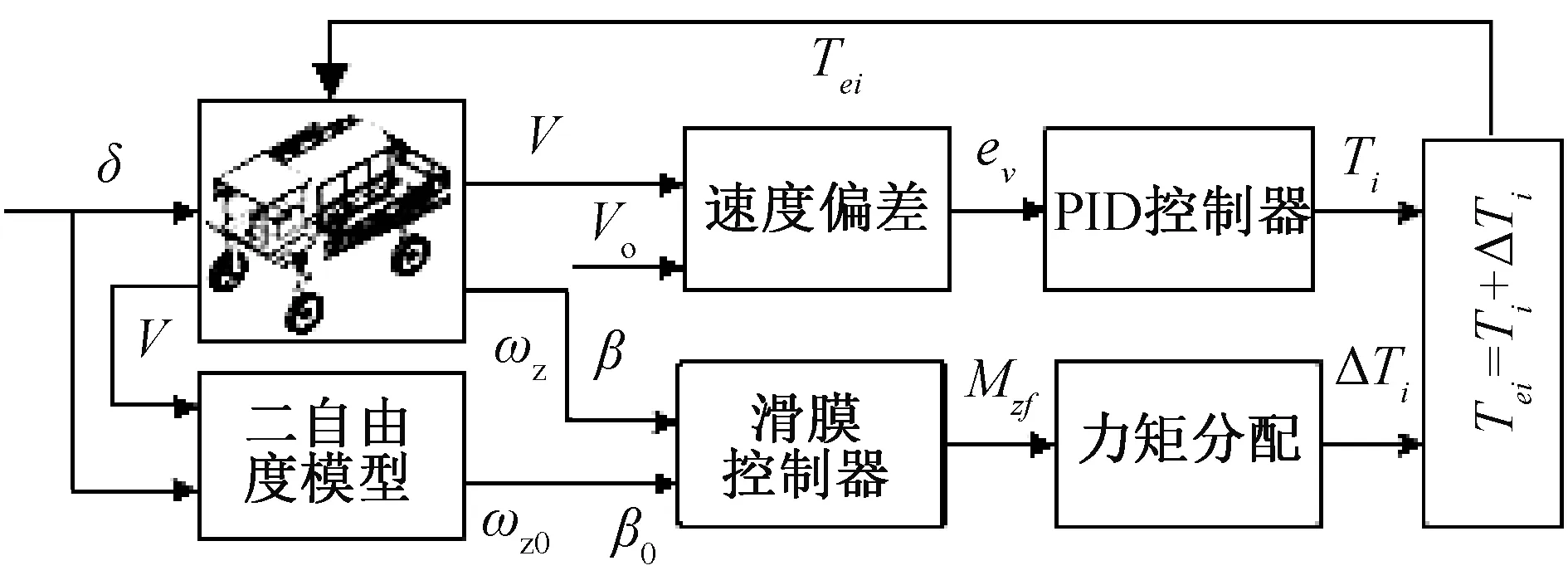
图4 整车力矩控制器原理
2.2 滑模控制器
本文基于滑模变结构控制理论设计滑模控制器,其原理是通过引入附加横摆力矩Mzf的方式主动干预4个车轮的驱动力矩,从而控制车辆横向稳定性。其工作过程主要包括趋近运动和滑模运动两个过程,当系统状态轨迹到达滑模面表现出在滑模面两侧来回穿越的现象,即抖振现象,并且抖振现象难以避免,只能减弱[13]。
引入附加力矩之后,横摆力矩计算公式(3)变为:
(14)
滑模函数的选择:
S(e)=(ωz-ωzd)+λ(βz-βzd),
(15)
式(15)中λ为滑模增益,其物理含义为表征质心侧偏角计算值与期望值误差相对于横摆角速度误差值对附加横摆力矩的影响程度。
对式(15)求导得:
(16)
由公式(10)、(14)得:
(17)
常见的滑模趋近率函数有符号函数、饱和函数、指数函数、幂次函数[14]。本文选择幂次函数代替理想滑动模态中的开关函数作为滑模趋近率函数,降低系统抖振现象,其表达式如下[15]:
(18)
式(18)中fal(s,α,ε)函数为线性连续的滑模面切换函数,当ε>0,且0<α<1时,可实现小误差大增益特性,本文取ε=0.01,α=0.5。
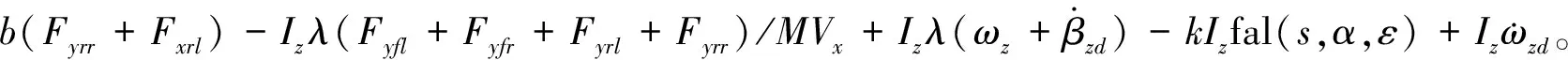
(19)
2.3 附加横摆力矩分配器
本文附加横摆力矩分配器采用同时改变4个车轮的驱动力矩的方式将上述所计算的附加横摆力矩平均分配到各个控制车轮上,从而保证车辆行驶轨迹的理想性,提高车辆作业行驶性能。此外,为了不改变车辆纵向动力学,需要保证纵向力不变。因此,同轴上的车轮分配的附加横摆力矩大小相同、方向相反,在车轮质心处产生的合力也大小相同、方向相反,同轴上纵向合力不变。而对于任意车轮,实施控制时所改变车轮的控制力矩大小需要在车身质心处产生相同大小的力矩,即1/4倍附加力矩。对于后轮而言,轮胎驱动力矩改变量在车辆质心处产生车辆维持稳定所需的1/4附加横摆力矩,即
(20)
从而可得:
ΔT=0.25r|Mzf|/d(记作S)。
(21)
其具体控制逻辑如表1所示。
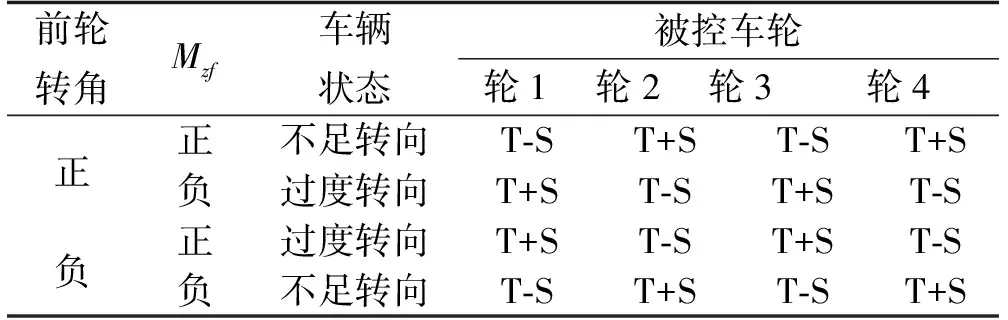
表1 车轮控制逻辑
3 仿真试验结果与分析
为验证所设计的横摆力矩稳定性控制方法的有效性,基于Matlab/Simulink 动态仿真软件建立包含Dugoff轮胎模型的七自由度非线性整车模型,将其作为控制对象进行仿真试验验证,其模型主要参数详见表2,并与无控制的仿真结果进行对比。

表2 整车主要参数
3.1 试验过程
(1)无控制试验。设计仿真初始速度为0.6 m/s,目标作业速度设置为1.5 m/s,路面附着系数μ取0.65,前轮转角输入如图5所示,图5中2.5~7.5 s之间是峰值0.087 rad、10 s为周期的正弦曲线。由于方向盘转角输入近似正弦输入[16],且不考虑方向盘到前轮转角的传递函数,因此,本文认为前轮转角也是近似的正弦曲线输入。Matlab/Simulink 采用 ode3 求解器,固定步长值 0.001 求解,仿真时长设定为10 s,并将整车中计算的附加横摆力矩值指定为0 N·m,即整车力矩控制器不起作用。
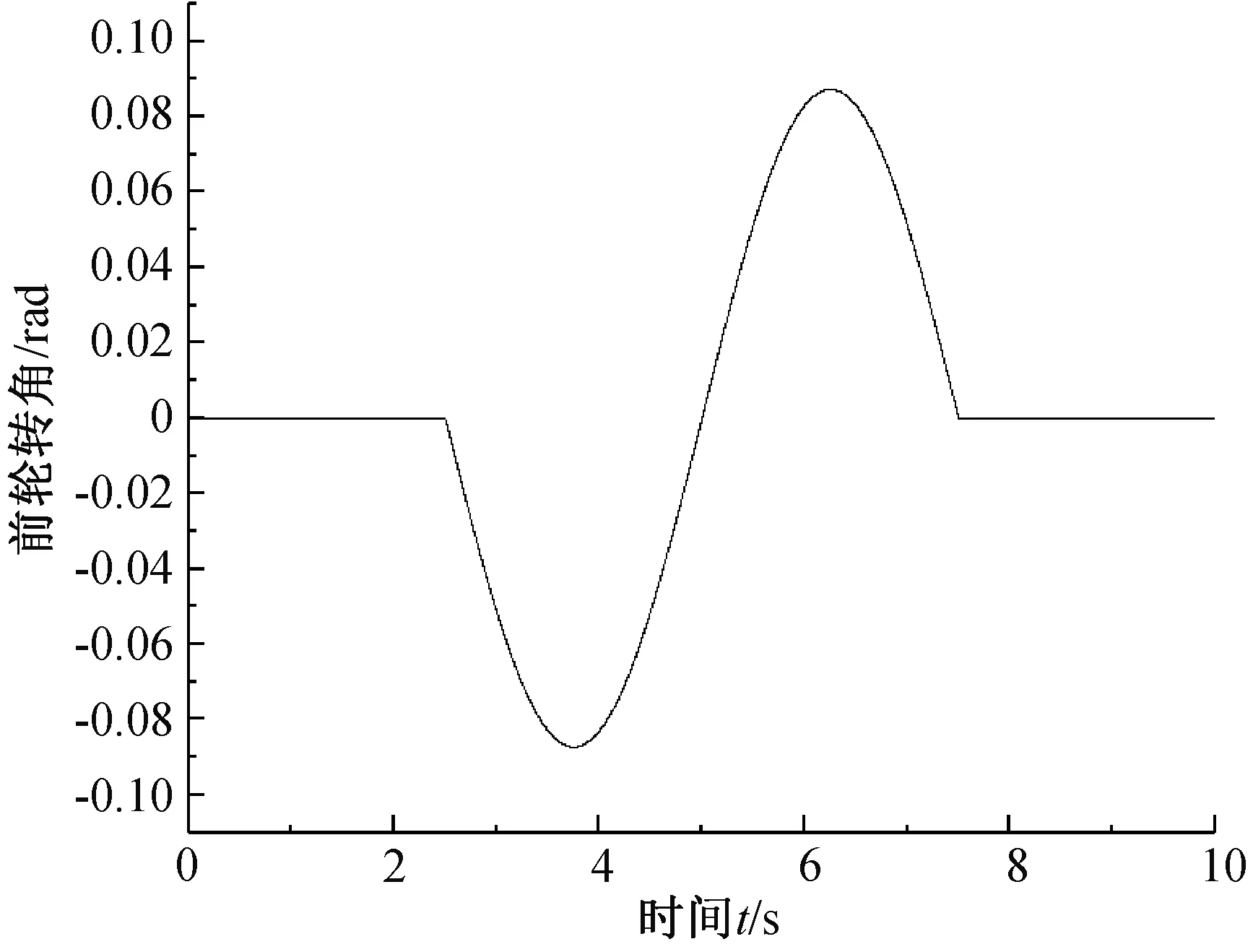
图5 前轮转角
(2)保持其他条件不变,接入整车力矩控制器,滑模增值依次给定为0、0.5、1.0、1.5,重复步骤(1)过程(原则上滑模增益值不能为0,但是该值为0时,可以看作是该值趋近于0时的极限值)。观察横摆角速度和质心侧偏角的变化趋势发现:该值大于1时,控制系统不稳定,横摆角速度和质心侧偏角发散;该值小于0.5时,相比于无控制时,横摆角速度和质心侧偏角变化并不是很明显;该值大于0.5小于1时,相比于无控制时,横摆角速度和质心侧偏角变化都能很好地随给定值变化。由此推测该值的最佳值在(0.5,1.0)区间。
(3)保持其他条件不变,接入整车力矩控制器,滑模增值依次给定为0.6、0.7、0.8、0.9,重复步骤(2)过程。观察横摆角速度和质心侧偏角的变化趋势发现,相比于无控制时,该区间内2个变量均能很好地随其给定值变化,但是在区间(0.8,0.9)横摆角速度能更好地跟随其给定值变化,而质心侧偏角在(0.5,1.0)区间变化不大,说明在区间(0.8,0.9)可能存在某一值,使横摆角速度能更好地随其给定值变化。
(4)保持其他条件不变,接入整车力矩控制器,继续给定该值为0.80、0.82、0.84、0.86、0.88、0.90,重复步骤(3)过程,观察横摆角速度和质心侧偏角的变化趋势发现,相对于无控制时,两者变化趋势均不明显了。这说明使横摆角速度和质心侧偏角随其给定值变化是区间(0.80,0.90)的任意一个值,最终确定该值为0.85。
3.2 结果与分析
仿真结果如图6至9所示,图6为横摆角速度响应,图7为质心侧偏角响应,图8为附加横摆力矩,图9为侧向位移。
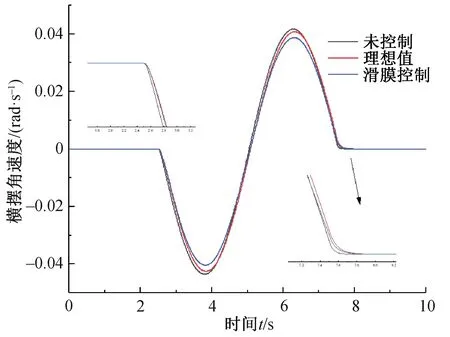
图6 横摆角速度响应
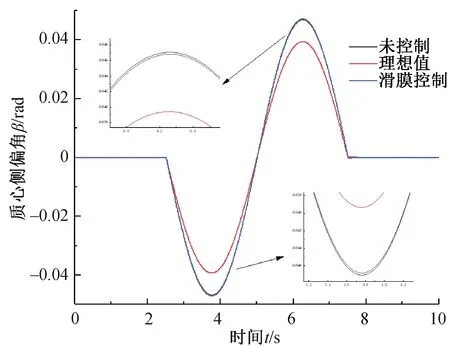
图7 质心侧偏角响应
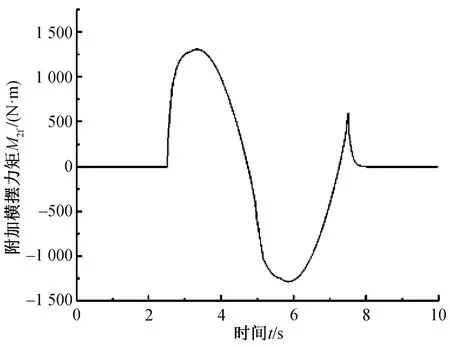
图8 附加横摆力矩
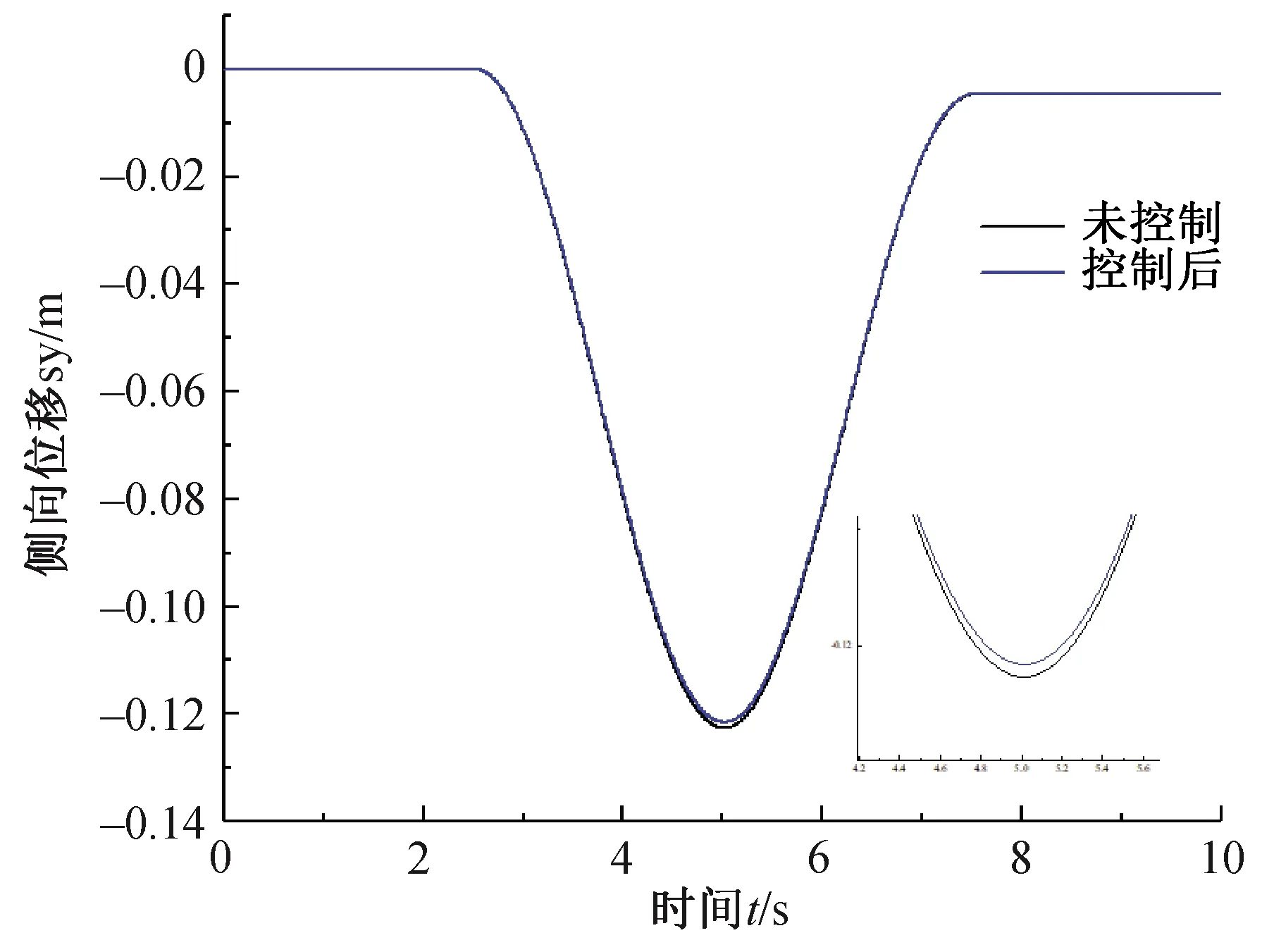
图9 侧向位移
(1)经过整车力矩控制器控制后,车辆各种状态参数都有了改善,特别是横摆角速度变化最为明显。从图6和图7可以看出,未控制工况下,横摆角速度和质心侧偏角都和给定值变化规律基本保持相同的走势,说明本文所建立的系统仿真模型的正确性。从控制效果来看,横摆角速度控制效果明显优于质心侧偏角(图6),在2.50~3.75 s和5.00~6.25 s变化过程中,给定值与滑模控制值之差的绝对值变化是由小变大,给定值与未控制值之差的绝对值变化是由大变小,并在3.75 s和6.25 s的邻域里,呈现出前者偏差的绝对值大于后者,在3.75 s~5 s和5 s~6.25 s之内,偏差绝对值变化呈现相反的情况。如图7所示,相同的情况在质心侧偏角响应曲线中也出现了。偏差变化绝对值由小变大,一方面说明控制效果起了作用,另一方面说明两个变量相互干涉,存在耦合现象。其次,相比于横摆角速度而言,目标控制量质心侧偏角的变化不明显,这主要因为车辆在低速工况下,其对于车辆稳定性的影响并不是十分突出,这同样体现在滑模函数的选择上。正如公式(15)中提到的滑模增益值,实则是质心侧偏角计算值与给定值之间的差值的权值,其值为0.85,对于横摆角速度计算值与给定值之间的差值的权值实则为1,从而使得横摆角速度和质心侧偏角的权值之比为20∶17,明显的可以看出,在一定附加横摆力矩的作用下,横摆角速度改善量显著于质心侧偏角。
(2)进一步分析各响应量的平均误差绝对值,结果(表3)表明:横摆角速度平均误差绝对值降低7.70%,质心侧偏角降低0.54%;另外,从图8可以看出侧向位移最大值减少0.02 m。这充分证明滑模控制能有效地控制车辆横向稳定性。

表3 响应量平均误差绝对值
4 结论
本文针对高地隙自走式喷雾机四轮驱动作业车辆特定工况,提出了附加横摆力矩控制的操纵稳定性控制策略;滑模控制器能够同时兼顾耦合变量横摆角速度和质心侧偏角对车辆横向稳定性的影响,并准确计算出需要施加的附加横摆力矩;设计的整车力矩控制器通过整合车辆行进力矩和附加横摆力矩分配器所分配的力矩对四轮驱动力矩及时适时控制,应对突变工况对车辆横向稳定性的干扰,仿真结果表明该控制策略能提高车辆低速时的操纵稳定性。
