基于动量自适应BP 神经网络的鸢乌贼模式识别

杨柳青青, 储莫闲, 刘必林,3,4,5,6, 孔祥洪,3

1. 上海海洋大学信息学院, 上海 201306;

2. 上海海洋大学海洋科学学院, 上海 201306;

3. 国家远洋渔业工程技术研究中心, 上海 201306;

4. 农业农村部大洋渔业开发重点实验室, 上海201306;

5. 农业农村部大洋渔业资源环境科学观测实验站, 上海201306

6. 大洋渔业资源可持续开发教育部重点实验室, 上海 201306;

21 世纪, 计算机科学进入了飞速发展的阶段,先进的神经网络结构和学习算法大量应用于人工智能领域, 机器视觉中的模式识别作为AI 的一个分支,其理论和技术也随之取得了巨大进步(毛振宇 等,2019)。近年来, 神经网络在人脸识别(陈艳, 2000)、电信号分类(王莉 等, 2019)、海岛识别(王振华 等,2020)、植物病害识别(邱靖 等, 2019)等领域得到了广泛应用。

头足类物种的种群遗传分化较小, 因此无法从分子遗传学水平来划分种群(李敏 等, 2019),而在生物生态学特性(Liu et al, 2013)、形态学特征等方面存在明显区别 (Kubodera et al, 1987)。角质颚是头足类的主要摄食器官(Clarke, 1962), 形态特征稳定(李建华 等, 2018), 常被用于头足类种类鉴定与种群判别(刘必林 等, 2009)。就种群判别而言, 过去的研究主要采用传统的统计学方法对角质颚形态进行判别。郑小东 等(2002)研究了我国华南莆田、南澳、深圳、湛江等4 个海域曼氏无针乌贼角质颚形态, 认为头盖长与脊突长的比值可用作区分不同地理种群的依据。许嘉锦(2003)研究发现, 台湾大溪与东港两地边蛸地理种群的角质颚形态分化明显。Liu 等(2015)、陈芃 等(2015)依据角质额各部长度的差异, 通过逐步判别法划分别对东太平洋茎柔鱼不同地理群体和西北太平洋柔鱼不同产卵群体进行了划分。然而, 这些研究的判别成功率都不高。

为此, 本文分别利用梯度下降法、单一动量法、单一自适应法和动量自适应法训练的多层BP 神经网络(back propagation neural networks)对西北印度洋、中东太平洋和南海等 3 个海区的鸢乌贼(Sthenoteuthis oualaniensis)的角质颚进行识别, 进而区分出鸢乌贼所属海域, 并探讨加入动量和学习率自适应的学习算法的优越性, 以及仅用角质颚进行识别的优缺点, 同时通过设计和训练得到高识别率的西北印度洋、中东太平洋和南海等3 个海区的鸢乌贼分类器, 为头足类种群判别提供新方法。

1 材料与方法

1.1 样本采集和数据测量

实验共采集鸢乌贼样本572 尾, 其中西北印度洋海区103 尾, 中东太平洋216 尾, 南海253 尾。冷冻的鸳乌贼样本首先在实验室自然解冻, 然后用卷尺测量胴长(mantle length, ML), 精确至1mm, 电子天平测量体质量(body weight, BW), 精确至0.1g。用镊子取出角质颚, 在清水中漂洗后用游标卡尺对上颚和下颚各 5 个特征进行测量, 精确至精度为0.01mm, 具体包括上头盖长(upper hood length,UHL)、上脊突长(upper crest length, UCL)、 上喙长(upper rostrum length, URL)、上翼长(upper wing length, UWL)、上侧壁长(upper lateral wall length,ULWL)、下头盖长(lower hood length, LHL)、下脊突长(lower crest length, LCL)、下喙长(lower rostrum length, LRL)、下翼长(lower wing length, LWL)、下侧壁长(lower lateral wall length, LLWL)(刘必林 等,2009)。

1.2 角质颚数据标准化

神经网络(neural network, NN)使用各特征值前,要对特征值进行标准化。首先, 将3 个海区转换成数字1、2、3, 以适合神经网络读取。其次, 由于在大样本训练集中, 神经网络会遗忘最初训练过的样本, 所以将3 个海区样本的顺序随机打乱进行训练。最后, 利用公式(1)将不规则数据归一化至[-1,1]之间(周开利 等, 2005)。

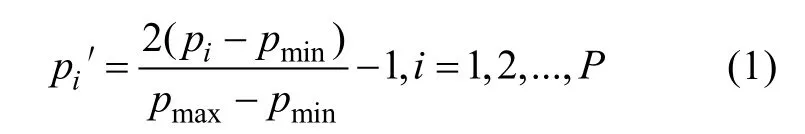
式中pi′表示标准化后的数据,pi表示标准化前的数据,pmin表示该特征中最小的数据,pmax表示该特征中最大的数据,P为样本总数

随后将标准化后的特征值数据集的90%划分为训练集, 剩下的10%作为测试集。

1.3 BP 神经网络的结构

BP 神经网络是一种有反馈的前向传播的NN,其层次结构可以分为3 大类: 输入层(I)、隐含层(H)和输出层(O)。其中I、O 层只能为1 层, 而H 层可为多层(图1)。设计一个BP 神经网络首先要确定的是其网络拓扑结构, 包括H 层层数和各层节点数(张德丰, 2018)。

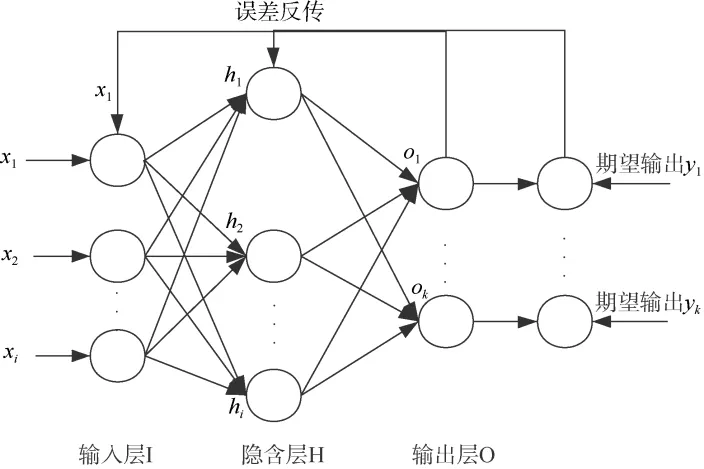
图1 BP 神经网络基本结构Fig. 1 The basic structure of BPNN

一般地, 当各节点均采用Sigmoid 型函数时,一个隐含层足以实现任意判决分类问题(Cybenko,1989), 且NN 的迭代次数(即对权值的回调次数)比起H 层的层数对识别正确率的影响更大(叶斌 等,2004)。本文中输入样本数为489, 根据袁曾任(1999)提出的算法(公式2), 通过设置H 层节点数为5～14,得当H 层节点数为9 时识别率最高, 且训练速度较快。I 层节点数11 个, 分别为ML、UHL、UCL、URL、UWL、ULWL、LHL、LCL、LRL、LWL 和LLWL; O 层节点数3 个, 分别代表西北印度洋、中东太平洋和南海。

式中J为输出节点数,n为输入神经元数,m为输出神经元数,a为1～10 间的常数。

确定网络拓扑结构后, 随机生成各权重和阈值,再带入样本参数进行前向传播和反馈调整。

1.3.1 根据输入进行前向传播

为了解决网络中线性不可分问题, 选用S 型函数Sigmoid 作为映射函数为公式(3),f(x) 取值范围为[0, 1], 其计算公式为

式中xi(i=1, 2, ... , I)为I 层中各节点的值;hj(j=1,2, ..., H)为H 层中各节点的值;αj为H 层第j个节点hj的阈值;ωji为I 层第i个节点到H 层第j个节点间的权值。

O 层中各节点的值为Ok(k=1, 2, ... , O), 表示此次通过网络拓扑结构计算预测出的海域, 计算公式为

式中kθ为O 层第k个节点ko的阈值,vkj为H 层第j个节点到O 层第k个节点间的权值。

1.3.2 对各层间的权重和各节点的阈值进行调整(反向传播)

基本原理是依据期望值和实际输出值的差值进行调整(图2)。本文中网络的方法为在δ的基础上增加动量项和自适应学习率, 以应对BP 神经网络存在的容易陷入局部最优解、学习效率低、收敛速度慢等问题(王莉莉 等, 2018), 具体方法如下。

(1)δ法调节权重

一次调整的大体方向是从后向前的, 依次为H层至O 层权值和O 层阈值的调整, 以及I 层至H 层权值和H 层阈值的调整。前者的校正误差影响后者的调整(图3)。将权值变更的值与误差的梯度下降成正比, 通过反复的调整减小误差。

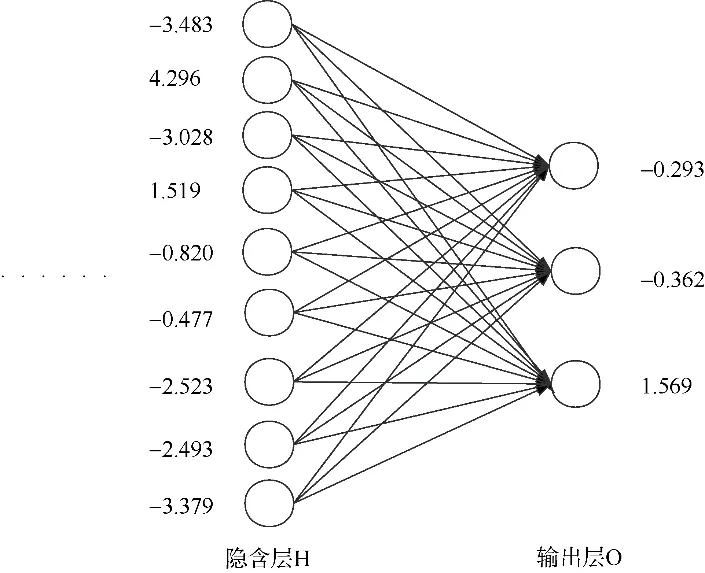
图3 H 层和O 层的阈值Fig. 3 The threshold value in hidden layer and output layer

① H 层至O 层权值和O 层阈值的调整

O 层的校正误差为dk=yk(1-yk)(ok-yk),k=1,2,…, H。H 层至O 层权值vkj计算公式为

式中vkj为H 层第j个节点到O 层第k个节点间的权值,hj为H 层第j个节点的值,η为学习系数(0＜η＜1),t 表示时刻,t+1 表示下一时刻。输出层阈值θ由以下公式确定:

式中θ(t+1)表示本次修正后(t+1 时刻)输出层阈值,θ(t)表示修正前(t时刻)输出层阈值,kθΔ 为输出层的阈值校正量。

② I 层至H 层权值和H 层阈值的调整

式中jiω为I 层第i个节点到H 层第j个节点间的权值,xi为I 层第i个节点的值,η为学习系数(0＜η＜1),t+1 时刻为本次修正后,t时刻为修正前, 隐含层阈值aj的计算公式为

式中jαΔ 为隐含层的阈值校正量。

重复上述步骤, 直至误差小于设定的精度(关小芳, 2014)或达到最大迭代次数。

(2) 引入动量因子

在权值校正量Δvkj和Δkjω中引入动量因子β(0≤β＜1) , 从而提升收敛速度, 计算公式为

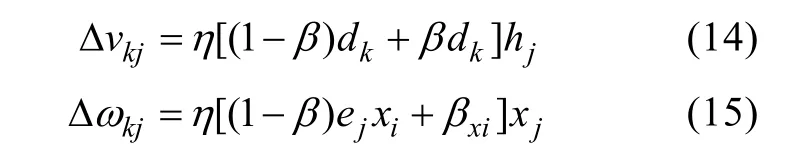
式中dk为输出层校正误差;ej为隐藏层矫正误差。同理, 可推出引入动量因子后的H 层和O 层阈值修正量。若上一次校正后, 输出值和期望值的方差更小,则β∈(0,1), 否则β=0。本文中当输出值更接近期望值时,β=0.9。

(3) 学习率可变(自适应)

学习速率η在Delta 中为常数, 这会导致当误差变化幅度小时, 训练次数增加; 而误差变化剧烈时,因调整步长较大, 跨过较窄的凹陷或突起区域, 使正确率下降, 收敛性差(关小芳, 2014)。因此, 除首次回调采用设定的学习速率, 之后都采取自适应学习速率(公式16)。当校正方向正确时, 校正步伐变大; 当校正方向错误时, 校正步伐减小(张德丰, 2018)。

式中γ为校正步长, 本文中校正方向正确时γ=1.05,校正方向错误时γ=0.7。

1.3.3 对BP 神经网络进行测试

经过以上步骤后, 本研究初步获得BP 神经网络鸢乌贼分类器, 接下来对其进行识别效果测试,并根据结果分析鸢乌贼角质颚的形态学特征。首先将测试样本带入, 观察识别情况; 若识别效果良好,则用预留下的测试样本对该分类器进一步测试, 观察其对陌生数据的泛化能力, 以防过度学习。

2 结果

2.1 角质颚数据转换

数的长度范围, 标准化后, 各特征值的极大值的绝对值均为1, 特征值为极大值的样本大多分布在南海, 少数分布在西北印度洋; 极小绝对值基本都在10-2以下, 全部分布在西北印度洋(表1)。当一个样本的一个形态参数为该形态参数全部样本中的极值, 该样本的其他形态参数很可能也为极值, 如第42 号样本的ML、UHL、ULWL、LLWL、LWL 均为极大值, 第464 号样本的UHL、URL、LRL 均为极小值。

表1 标准化后的极值和所属海域Tab. 1 The extreme value and its sea area after standardization

2.2 训练完成后的网络

2.2.1 各层权重和阈值

由图 4 可知, 迭代次数X=1492 时, 均方差Y=0.04416, 即I 层到H 层各节点的权重的绝对值大小基本都在10-1级以上, 可见鸢乌贼胴长和10个角质颚数据指标对用 BP 神经网络进行角质颚分类都是非常重要的(图4)。本研究中的BP 神经网络鸢乌贼海域分类器有 4 个关键数据矩阵, 分别是I 层和H 层间的权重(表2)、H 层和O 层间的权重(表3)、H 层各节点的阈值以及O 层各节点的阈值(图3)。I 层11 个节点分别表示鸢乌贼的胴长和10 个角质颚特征值。权重的绝对值越大, 表示前一层节点对后一层节点的影响越大。在I 层到H层的99 个权重中绝对值大于2 的有5 个, ML 和ULWL 特征参与的分别有2 个, UCL 特征参与的有1 个; 绝对值大于1.5 的权重中5 个的前驱节点是ULWL, 接下来依次是LHL、ML、UCL 和LLWL。因此, ULWL 对种族间差异的贡献最大, 其次是ML 和LHL。

表2 I 层和H 层间的权重Tab. 2 The weights between input layer and hidden layer

图4 神经网络训练效果Fig. 4 Neutral network training effect

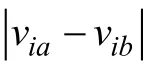
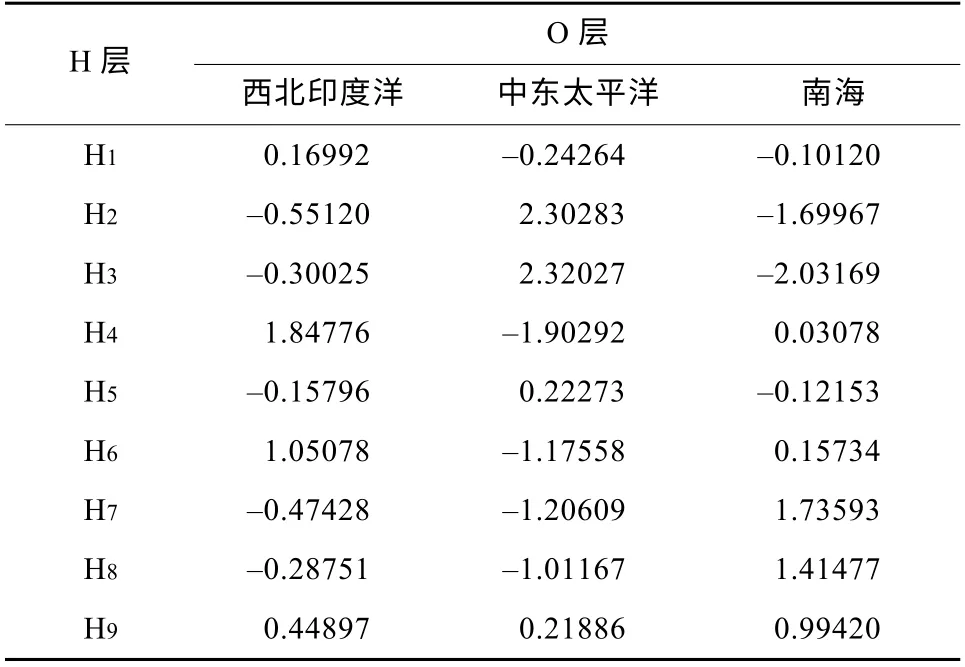
表3 H 层和O 层间的权重Tab. 3 The weights between hidden layer and output layer

9 个H 层节点和3 个O 层节点的阈值, 后者分别表示3 个海区的判别阈值, 西北印度洋为-0.293,中东太平洋为-0.362, 南海为1.569(图3)。

2.2.2 网络训练情况

y轴的均方误差为O 层实际输出和期望值的方差, BP 神经网络随着迭代次数的增加而收敛, 经过1492 次迭代后就已收敛至目标误差, 其误差为4.416×10-2(图4)。

2.3 成型网络的识别效果

2.3.1 对于训练集的识别效果

运用动量自适应BP 神经网络对鸢乌贼进行海区识别的总体准确率可达到92.77%, 其中西北印度洋、中东太平洋和南海识别率分别为 88.89%、89.95%和96.80%(表4)。中东太平洋和南海鸢乌贼发生相互误判的数据为24 组, 占所有误判数据的66.66%。

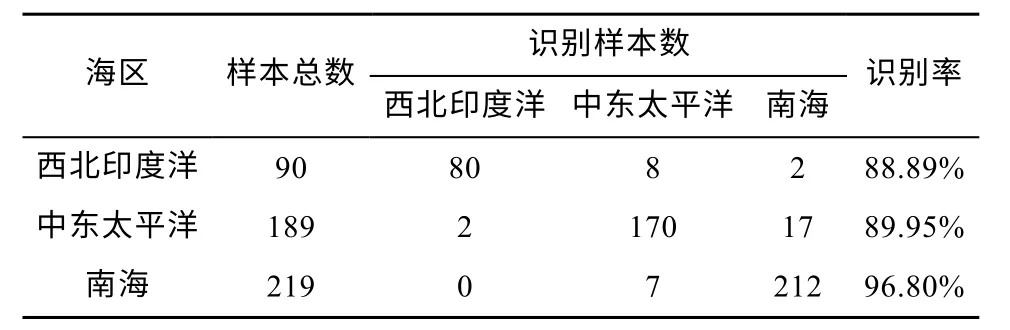
表4 动量自适应学习方法下训练集识别结果Tab. 4 The recognition results of the training set with the momentum adaptive learning method

2.3.2 对于测试集的识别效果

由于对训练集的识别效果良好, 用测试集进一步测试识别效果。对鸢乌贼角质颚测试集进行海区识别的总体准确率可达到93.24%, 其中西北印度洋、中东太平洋和南海识别率分别为100%、88.89%和94.12%。西北印度洋的角质颚识别率最高, 达到零误差, 而且中东太平洋和南海的鸢乌贼不会被误判到西北印度洋海区(表5)。

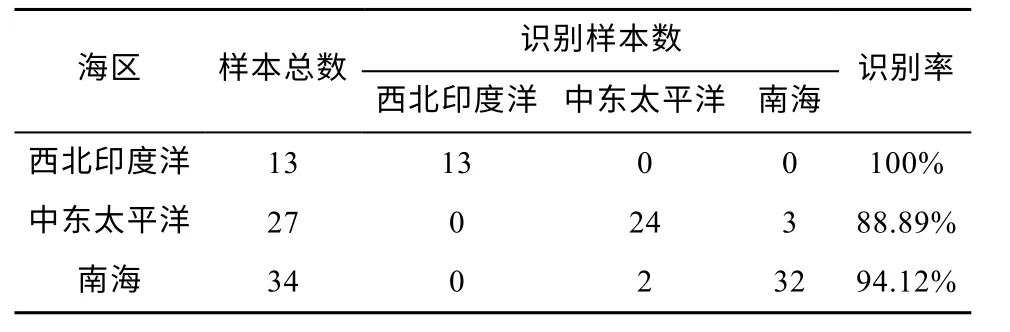
表5 动量自适应学习方法下测试集识别结果Tab. 5 The recognition results of the test set with the momentum adaptive learning method

2.3.3 其他学习方法的识别效果

若只采用传统的梯度下降法(δ法), 西北印度洋、中东太平洋和南海的识别率分别为46.15%、70.37%和88.24%, 总识别率为74.32%。引入动量因子后, 西北印度洋的识别率上升至53.85%, 中东太平洋的识别率仍为70.37%, 南海的识别率小幅上升至91.12%, 总识别率为77.03%, 比传统方法上升约3%(表6)。

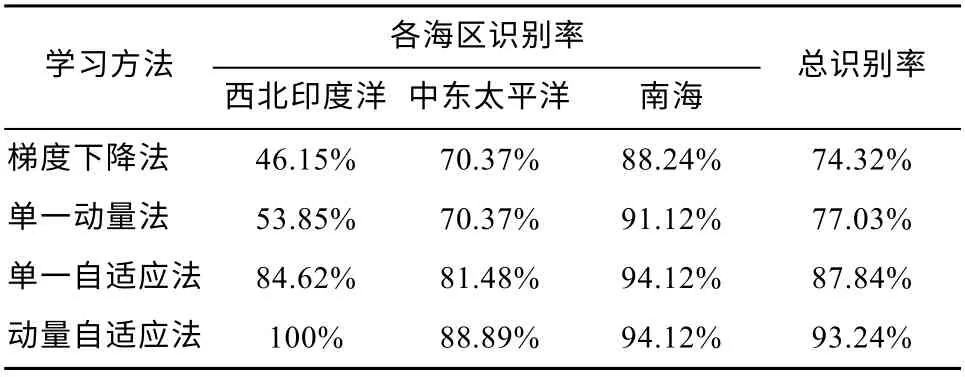
表6 各种BP 学习方法的识别效果Tab. 6 The recognition results with different sorts of BPNN learning methods

为学习率加入自适应调节后, 西北印度洋、中东太平洋和南海的识别率分别大幅上涨至84.62%、81.48%和 94.12%, 该学习方法的总识别率为74.32%, 比传统方法识别率高10%。

2.3.4 仅使用角质颚数据的识别效果

若是不采用胴长数据, 只用10 个角质颚参数进行BP 神经网络动量自适应法分析识别, 西北太平洋、中东太平洋和南海的识别率分别为84.62%、81.48%和91.18%, 均有7%～15%不同幅度的下降。

3 讨论

3.1 BP 神经网络中动量自适应学习方法与传统学习方法δ的比较

传统的BP 神经网络学习算法具有容易陷入局部最优解和学习速度慢的缺点, 为证明动量和自适应学习率引入的必要性, 将其识别效果和传统学习方法、单一动量学习方法和单一自适应学习方法(学习率可变)进行对比。

动量法即在权值修正量中引入动量因子, 以减小振荡趋势, 改善其收敛性, 从而提高网络训练速度。自适应法将学习率从传统BPNN 中的固定值变为动态值, 从而避免了在平坦区域内学习率太小导致训练次数增加, 和在误差变化剧烈的区域中学习率太大导致忽略极高或极小区域的问题, 这两个问题会延长达到目标方差的时间, 增加迭代次数。用传统学习方法的鸢乌贼分类器对西北印度洋鸢乌贼的识别率低至 46.15%, 不及动量自适应方法的50%(表5)。而总体上看, 动量自适应方法的识别率也比传统方法上升19%, 且各个海域的识别率均有上升。其中动量(学习率可变)的引入尤为关键, 单一动量的引入就使总识别率上升10%。因此, 动量和可变学习率的引入对分类器识别率的提升至关重要,这也验证了传统BP 神经网络容易陷入局部最优解的问题。

3.2 模式识别和其他判别方式的比较

传统的分子生物学方法判别头足类的种类实验操作比较复杂, 并且在分类地位比较相近的种类,尤其种群之间的判别效果不明显。角质颚形态结构稳定, 且数据采集方式便利, 所以, 利用角质颚形态来判别头足类的种类和种群比分子生物学方法便捷许多。有学者利用角质颚形态特征差异划分了西北部印度洋、中西太平洋和热带东太平洋3 个海区的鸢乌贼种群, 结果总体交叉验证判别正确率为63.5%(Liu et al, 2018)。然而, 本研究所采用的方法更加准确, 判别准确率提高了近20%。但是, 动量自适应BP 神经网络的不足之处在于需要采集大量样本对网络进行训练。而且, 由于构建BP 神经网络缺乏统一的标准, 各节点间的权重和各节点的阈值的初始值为随机数, 所以每次训练得到的NN 识别率会有3%以内的误差。不过这一缺点可以通过多次训练, 保存识别率最高的网络来弥补。

3.3 胴长对识别结果的影响

由于角质颚能长久储存生物特征, 且已有研究证明角质颚能存储体长信息(Clarke, 1962; 徐杰 等,2016; 李建华 等, 2018), 故去除胴长参数、仅用角质颚进行判别。然而其识别率比加入胴长数据的总识别率下降近7%, 这可能是因为不同海域的鸢乌贼体型大小差异所致。虽然大多数鸢乌贼角质颚大小与胴长成正相关, 但是仍有少数鸢乌贼胴长较长,角质颚却较小, 导致误判。

4 结论与展望

本研究首次基于BP 神经网络实现鸢乌贼海域分类器, 并加入动量和可变学习率对其进行改进,同时为头足类种群判别提供新方法。利用前馈反向神经网络结构和动量自适应学习算法, 对标准化后的鸢乌贼角质颚和胴长形态参数进行训练, 经过1492 次迭代后就已收敛至目标误差, 其误差为4.416×10-2, 用测试集检测得出的神经网络的总正确率为93.24%。网络对西北印度洋、中东太平洋和南海等3 个海区的识别正确率分别为100%、88.89%和94.12%, 高于传统学习方法、单一动量学习方法和单一自适应学习方法。经实验证明, 学习率自适应对判别正确率的影响更大。若去除胴长参数, 总识别率为86.49%。可见, 虽然鸢乌贼角质颚能储存较完整的年龄和胴长信息, 但是有一定局限性。

在实际应用时, 根据4 个数据矩阵(表2、表3和图3)可以直接得出西北印度洋、中东太平洋和南海等 3 个海区鸢乌贼所属海域的分类器, 省去数据采集、存储和训练神经网络所需的时间, 将所要识别的鸢乌贼的相关数据根据训练样本根据训练集各特征值的极值(表1)归一化后, 代入分类器即可, 进行高效率、低设备处理和存储能力要求的识别工作。

此方法目前只支持西北印度洋、中东太平洋和南海等3 个海区鸢乌贼之间的识别, 若加入其他海域的鸢乌贼数据, 或用于其他头足类的不同海域间的识别, 结果如何还有待进一步研究。